平面薄膜结构找形及张紧结构数值对比分析
2021-12-14王旭飞沈酉庆寇子明
王旭飞,张 静,沈酉庆,寇子明
(太原理工大学机械与运载工程学院,太原 030024)
0 引言
随着航天事业的发展,平面薄膜结构凭借其质量轻、折展比高、易折叠等优势,逐渐成为太阳帆、遮阳罩、空间可展天线等航天器结构的重要发展方向[1-4]。为了确保薄膜在轨展开后达到正常的工作状态,其表面形状需要满足平衡条件和结构要求。因此,对平面薄膜结构的膜面形状进行找形分析具有重要意义。
平面薄膜结构主要由薄膜、张紧结构和边框支撑结构组成。其中张紧结构主要分为一级张紧结构和二级张紧结构[5]。在一级张紧结构中,分布在薄膜边界的索(边索)直接穿过薄膜边缘处的索套,其两端与角点支座相连,从而实现膜面的张拉;二级张紧结构中的索主要包含内索和外索等,两者在每一跨通过连接点或中间索进行连接,通过内索、外索、固定支座在平面薄膜结构角点处的配合,以实现薄膜膜面的张拉。在平面薄膜结构中,评价膜面性能的主要指标有膜面基频、有效面积率以及应力分布均匀度等[2]。
薄膜结构的找形方法主要有力密度法[6-7]、动态松弛法[8-9]和非线性有限元法[10]。由于有限元软件的广泛应用,国内外学者大多使用非线性有限元法进行找形分析,并对膜面性能的影响因素做了大量研究。汪有伟等[4]通过非线性有限元找形分析发现,较之一级张紧结构,二级张紧结构可以减缓褶皱的发生。肖薇薇等[11]采用非线性有限元法研究了不同边缘索曲线形状对平面薄膜结构中膜面基频和应力分布均匀度的影响。丁潇等[5]采用非线性有限元法对平面薄膜结构进行找形分析,研究了索力和张紧形式对膜面有效面积率、基频和支座反力的影响。项平等[12]采用非线性有限元法对不同张紧结构的平面薄膜进行了找形分析,结果表明二级张紧结构的膜面应力分布均匀度低于一级张紧结构。目前已有的研究主要集中于索力、结构边界形状和张紧形式对膜面有效面积率以及应力分布均匀度的影响,较少考虑膜面预应力、厚度、跨数对膜面有效面积率、基频和应力分布均匀度的影响。
二次找形法则是对非线性有限元法的二次使用[13],其具体分析过程为:第1 次采用非线性有限元法时,通常将薄膜和索的弹性模量降低2 个数量级,使膜面和索柔软到可以自由变形,再对其施加初始预应力和边界条件,得到应力分布相对均匀的初始近似曲面,此过程也被称为小弹性模量法;之后,将初始近似曲面进行第2 次非线性有限元分析,输入薄膜和索的真实弹性模量,最终可得到较为精确的曲面[14]。由文献[15]可知,二次找形法具有收敛速度快,收敛性好等优点,且已广泛应用于建筑薄膜结构找形,但在空间平面薄膜结构上的应用却极少。
本文采用二次找形法,对一级张紧结构和含中间索的二级张紧结构时的平面薄膜结构进行了找形分析,并通过改变膜面预应力、厚度、跨数等参数,分析其对基频、有效面积率以及应力分布均匀度的影响,为结构分析提供数值参考。
1 张紧结构中预应力计算方法
1.1 一级张紧结构
由胡克定律知,一级张紧结构中边索预张力T和膜面预应力F[4]为:
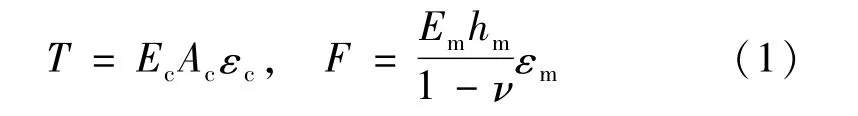
式中:Ec为边索的弹性模量;Ac为边索的截面面积;εc为边索的应变;Em为薄膜的弹性模量;hm为薄膜厚度;ν为薄膜的泊松比;εm为薄膜的应变。
由于建模时边索单元与膜单元之间共享节点,为了避免薄膜出现褶皱,同时减少膜面与边索之间的摩擦[4],应使边索与薄膜的应变值保持一致。通过对应变值进行设定,可求得一级张紧结构中薄膜和边索的预应力。
1.2 二级张紧结构
在一级张紧结构中,相邻两支座之间计为一跨,如果薄膜的任意一条边有S个支座,则此结构的跨数为S-1;在含中间索的二级张紧结构中,相邻两中间索之间计为一跨,若此结构的中间索数目为M,则其跨数为M-1。
在对张紧形式为二级张紧结构(含中间索)的薄膜结构进行整体找形时,为使膜面能够处于理想的平衡状态,需确定各索的预张力,即索力大小。在此以中间索数目为6,跨数为5 的二级张紧结构为例,进行索力的分析计算。
为了简化找形过程,将如图1 所示的二级张紧结构拆分成5 跨的一级张紧结构、中间索和外索三部分。首先取出内索和膜面,将内索与中间索的连接点处设置成固定支座,此结构相当于5 跨的一级张紧结构[5],并对其完成找形分析;然后将结果中的各个支座反力作为中间索的预张力;最后,通过力的平衡分析以完成外索索力大小的确定。
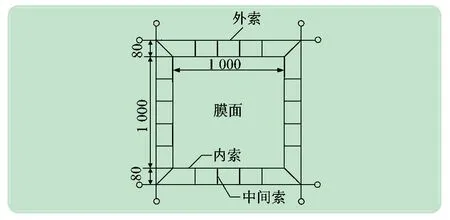
图1 跨数为5的二级张紧结构的初始模型(mm)
为使中间索在找形之后仍能基本维持竖直或水平状态,对外索施加满足平衡条件的预张力。假设索力平衡时张紧结构形态如图2 所示。

图2 假设平衡时张紧结构形态
若α1、α2中任意一个角度值为已知,即可求得外索预张力T1、T2和T3,即:
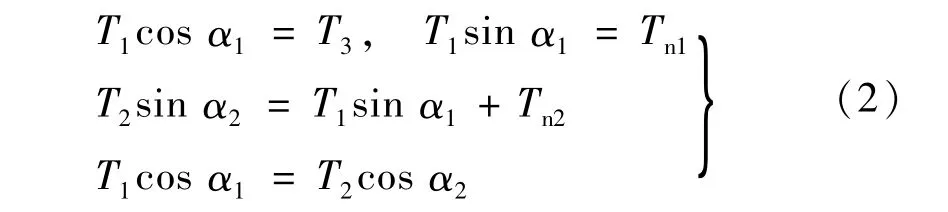
式中:Tn1、Tn2、T4为中间索的预张力;α1、α2为外索与水平线之间的夹角。
2 一级张紧结构下找形及数值分析
利用ABAQUS软件,对平面薄膜结构进行找形分析,薄膜采用聚酰亚胺材料,索采用Kevlar 材料,其中薄膜和索的具体参数见表1。
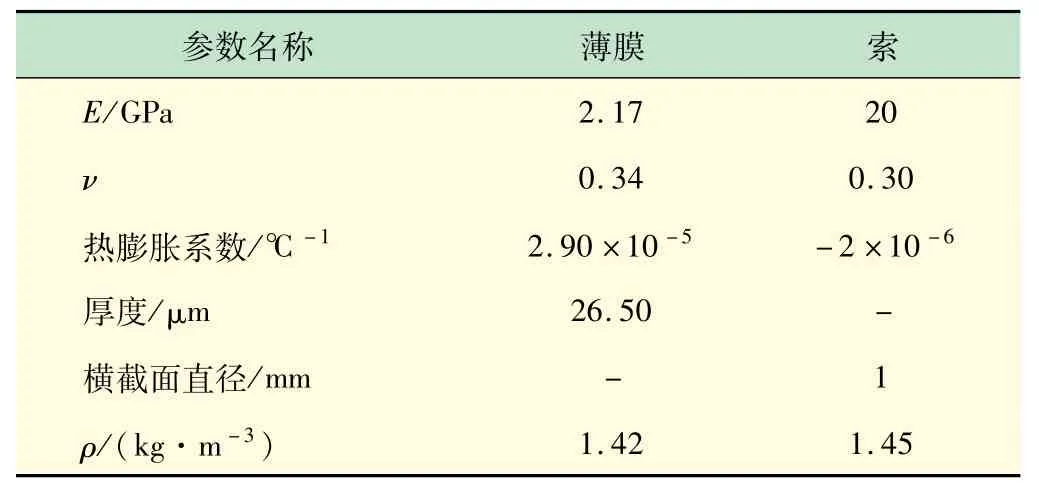
表1 薄膜和索的参数
有限元模型中,薄膜采用S3 壳单元,索采用T3D2桁架单元,薄膜和边索进行绑定约束,并对边索处4 个角点施加完全固定约束。另外,对于含中间索的二级张紧结构,内索与中间索的连接点、中间索与外索连接点均进行绑定约束。整个分析过程均涉及几何非线性[15]。
2.1 一级张紧结构下的找形分析
建立如图3 所示的初始模型,其中方形膜面边长为1 000 mm。根据式(1),取εc=εm=0.20%,可计算得到薄膜的预应力与边索的预张力分别为1.23、31.60 N。利用降温法[16]分别对薄膜和边索施加预应力。
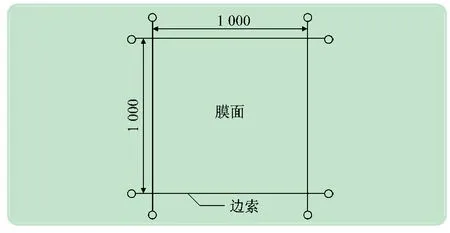
图3 一级张紧结构的初始模型(mm)
经过两次找形后得到的膜面应力分布结果分别如图4 所示。
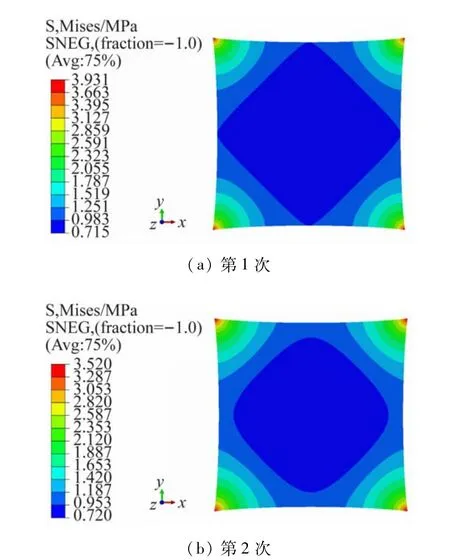
图4 两次找形后膜面应力分布云图
由图4 可知,第1 次小弹性模量找形与第2 次找形后的几何形态相似。第1 次找形后的膜面应力分布范围为0.715~3.931 MPa;第2 次找形后的膜面应力分布范围为0.720~3.520 MPa。由于第1 次找形时使用的弹性模量较小,使薄膜能够柔软地进行张拉,因此造成两次找形应力分布范围相差较大。
经过两次找形后的薄膜更加真实且更能满足结构要求,同时也验证了二次找形法的可行性和实用性。此外,找形后的膜面并非等应力分布,造成此现象的原因主要有两点:①薄膜和边索的连接方式会影响膜面应力分布;②角点处为完全约束形式,极易导致此处的薄膜出现应力集中现象,进而使膜面应力分布不均匀。
2.2 基频的影响因素
基频是结构振动特性的重要参数。对于平面薄膜结构来说,基频越大,其刚度也就越大。本文分析了一级张紧结构中薄膜厚度不同时,膜面预应力、跨数对膜面基频的影响。
(1)膜面预应力对基频的影响。边索预张力保持31.60 N不变,对薄膜厚度为26.50~200 μm、膜面预应力分别为0.5、0.75、1、1.23、1.50 和2 MPa 时的平面薄膜结构进行找形分析,结果如图5 所示。
由图5 可知,当薄膜厚度保持不变,且膜面预应力由0.5 MPa增大到2 MPa 时,膜面基频呈现较快的增长态势。当膜面预应力保持不变时,基频随薄膜厚度增大而减小。
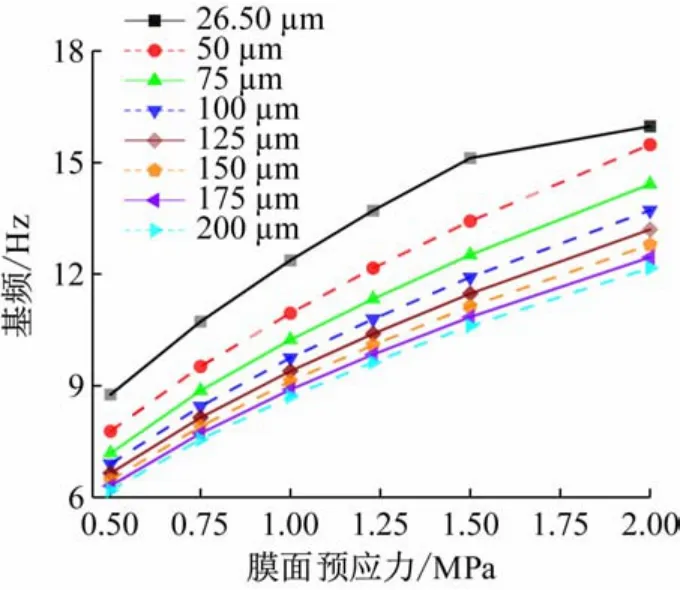
图5 不同薄膜厚度下基频随膜面预应力的变化曲线
(2)跨数对基频的影响。在保证一级张紧结构中膜面预应力与边索预张力不变的前提下,分析了跨数对膜面基频的影响,结果见表2。
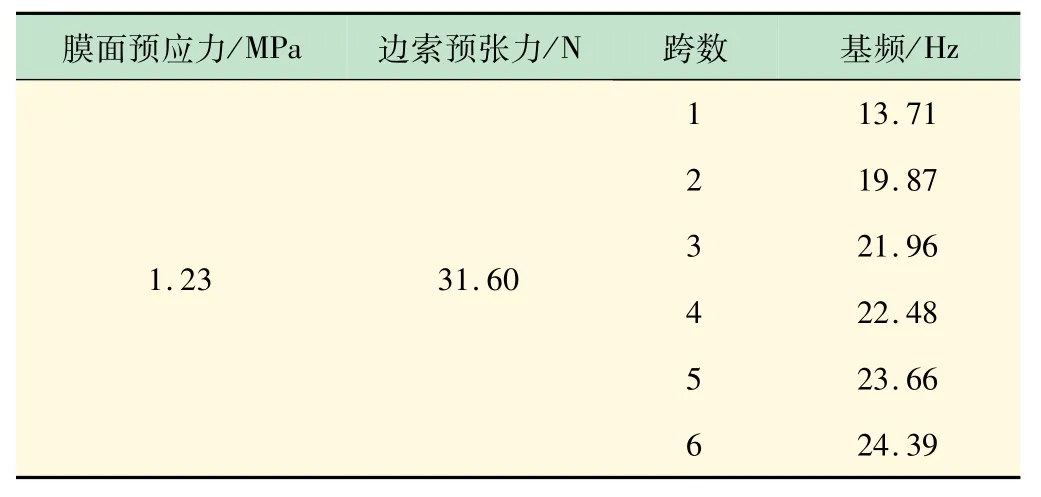
表2 不同跨数下的膜面基频
由表2 可知,在一级张紧结构中,基频随着跨数的增多而增大,意味着薄膜的膜面刚度也随之增大。
2.3 有效面积率的影响因素
平面薄膜结构的有效面积是指找形分析完成后索膜边界曲线所围形状的内切矩形面积,有效面积率是指该面积与边框围成的矩形面积之比,它是平面薄膜结构的重要设计指标[5]。
(1)膜面预应力对有效面积率的影响。在薄膜厚度为26.50~200 μm、边索预张力为1.23 MPa 时,对平面薄膜结构的有效面积率进行分析,其中膜面预应力的取值与2.2(1)节中相同。结果曲线如图6 所示。

图6 不同薄膜厚度下有效面积率随膜面预应力的变化曲线
由图6 可知,当边索预张力保持不变时,有效面积率随膜面预应力的增大而减小,且不同厚度薄膜对应的有效面积率的变化趋势是相同的。当膜面预应力保持不变,薄膜厚度从26.50 μm 增大到200 μm 时,膜面有效面积率的变化幅度不大;但随着膜面预应力增大,相近厚度薄膜的有效面积率的变化幅度也随之增大。
(2)跨数对有效面积率的影响。在膜面预应力为1.23 MPa和边索预张力为31.60 N不变的情况下,研究跨数对有效面积率的影响,结果如图7 所示。

图7 不同跨数下的有效面积率
由图7 可知,当跨数从1 增大到6 时,膜面有效面积率也随之增大,但其增长速率逐渐放缓。当一级张紧结构的跨数为6 时,其有效面积率高达98.50%。
2.4 应力分布均匀度的影响因素
采用膜面所有节点的Mises应力均方差值与其均值的比值作为膜面应力分布是否均匀的衡量标准,并将此比值称为应力波动系数φ。φ 越小,表明膜面应力分布越均匀[11]。膜面所有节点的Mises 应力均方差值σ计算公式如下:
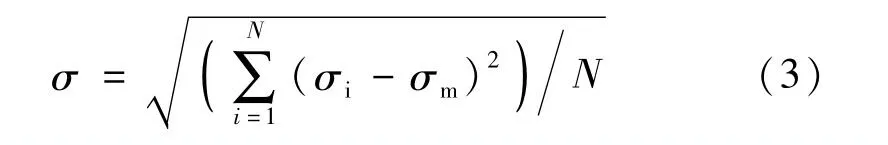
式中:σi为膜面节点应力的仿真值;σm为所有节点应力的均值;N为节点总个数。
(1)膜面预应力对应力分布均匀度的影响。膜面预应力对应力分布均匀度的影响分析是在薄膜厚度为26.50~200 μm、边索预张力保持1.23 MPa不变的情况下进行的,其中膜面预应力的取值与2.2(1)节中相同。结果如图8 所示。
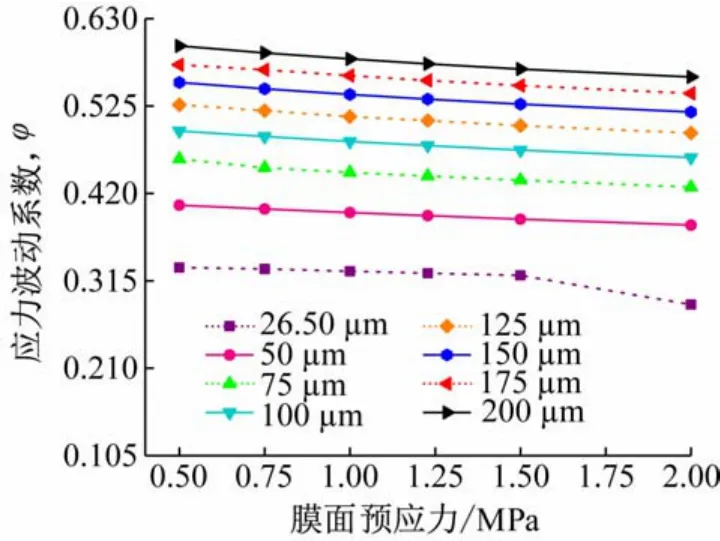
图8 不同薄膜厚度下φ随膜面预应力的变化曲线
由图8 可知,当薄膜厚度一定时,应力波动系数随膜面预应力的增大而减小,表明当膜面预应力在一定范围内取值时,膜面应力分布随着膜面预应力增大会越均匀,此时薄膜越不易形成褶皱。保持边索预张力和膜面预应力不变,随着薄膜厚度增大,膜面应力波动系数也随之增大,则膜面应力分布越不均匀。
(2)跨数对应力分布均匀度的影响。保证一级张紧结构中膜面预应力为1.23 MPa 与边索预张力为31.60 N不变的前提下,研究了跨数对φ的影响,结果曲线如图9 所示。
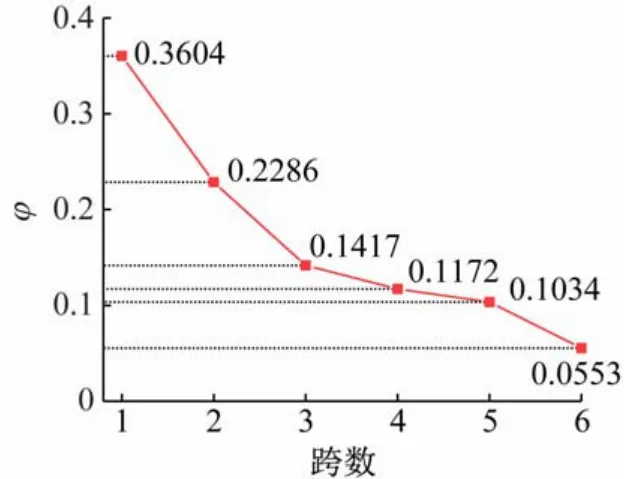
图9 跨数对φ的影响曲线
由图9 可知,当跨数为1~6 时,膜面应力波动系数随着跨数的增多而减小,表明膜面应力分布越均匀。
3 二级张紧结构下的找形及结果对比分析
3.1 二级张紧结构下的找形分析
在膜面预应力为1.23 MPa 不变的条件下,通过1.2 节中索力计算方法得出各个索力大小,采用二次找形法对如图1 所示的模型进行找形,其中,方形薄膜边长为1 m,结构中角点处中间索长度为,其余中间索长度均为80 mm。图10 为跨数为5 的二级张紧结构找形后的膜面Mises应力分布云图。
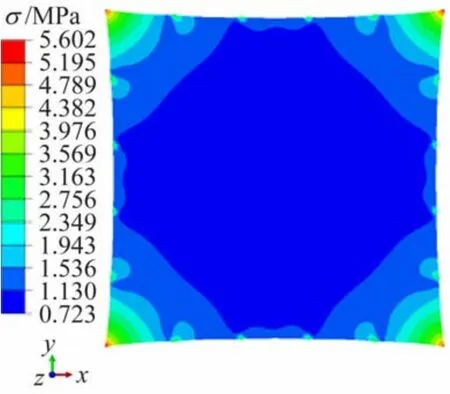
图10 膜面Mises应力分布云图
通过图10 可得,薄膜结构找形后膜面应力分布范围为0.723~5.602 MPa,其中膜面在中间索与内索连接点处以及4 个角点处的应力值较大。
3.2 不同张紧形式下找形结果对比
对4、5、6 跨的二级张紧结构进行找形,并将其与同等跨数下的一级张紧结构的找形结果进行对比分析,结果见表3。

表3 跨数为4、5、6 的一级张紧结构与二级张紧结构的找形结果对比
由表3 可知,在膜面预应力相同条件下,相同跨数的二级张紧结构与一级张紧结构相比,其有效面积率和基频均较小,但应力波动系数较大。
4 结论
本文利用ABAQUS软件,针对膜面尺寸为1 m×1 m的平面薄膜结构进行了找形分析。探究了一定条件下,不同的张紧形式、膜面预应力等参数对膜面有效面积率、基频和应力分布均匀度等性能指标的影响,得出了以下结论:
(1)在一级张紧结构中,基频和应力分布均匀度与膜面预应力和跨数的变化均成正相关。随着跨数增多,有效面积率也随之增大,但当膜面预应力逐渐增大时,有效面积率反之减小;
(2)相同的膜面预应力和跨数下,与二级张紧结构相比,一级张紧结构的有效面积率和基频较大,应力波动系数较小,表明在此条件下,一级张紧结构的膜面性能要优于二级张紧结构。
