考虑LMP的城市电动汽车充电站优化配置

2021-12-14文家利刘友波

实验室研究与探索 2021年10期

文家利，刘友波，黄媛，向月

（四川大学电气工程学院，成都 610065）

0 引言

近年来，随着电池技术取得了重大突破，同时响应国家“绿色发展”战略，各大汽车制造商重点打造新能源汽车产业，尤其是纯电动汽车［1］。然而，城市充电服务网络的不完善制约着电动汽车的发展，电动汽车充电负荷大量接入配电系统也会造成配电系统出现阻塞现象，不仅对电网公司造成经济损失，而且会影响企业投资者的决策。充电配套服务不仅对电动汽车制造企业很重要，对电动汽车用户更加重要。消费者购买电动汽车时会重点考虑充电问题，而企业在推广电动汽车时若没有配套充电设施，消费者会退缩，会阻碍电动汽车的普及。随着国家政策出台，越来越多的企业开始投资电动汽车充电站［2］，综合多维信息进行电动汽车充电站规划是投资者亟需解决的问题。

目前，国内外研究学者对电动汽车充电负荷预测和充电设施规划进行了大量研究，其中文献［3］中建立了以投资成本为目标函数，重点考虑交通信息作为约束条件，并用量子粒子群算法进行求解。文献［4-5］中以电动出租车为对象，充分研究其运行特性，分别以总耗时和总耗时费用为目标函数，建立了电动汽车充电设施优化配置模型。文献［6］中综合考虑道路信息、车流信息和配电系统拓扑结构，以电动汽车用户的损耗成本和充电站线路投资成本之和为目标函数，并考虑配电系统容量约束，构建了充电站的选址定容模型。文献［7］中从社会企业角度出发，研究了社会企业投资电动汽车充电站规划时应考虑的因素，运用双层规划理论建立了电动汽车充电站优化配置模型，能实现社会投资者和电动汽车用户各自利益的有效折中。文献［8］中将城市规划区域划分为多个正方形区块，以总投资费用最小为目标函数建立了充电设施规划模型，约束条件包括服务半径、充电容量等。文献［9］中提出了一种两步优化选址模型，先利用免疫算法获得规划区域内充电站待选点，后利用模糊层次分析法进行综合量化并确定最有选址。上述研究成果对电动汽车充电站的规划具有重要的指导意义，而在电力市场环境下电动汽车大量接入电网引起电网阻塞问题等方面鲜有研究，在规划中进行重点考虑具有重要的工程价值。

基于上述背景，本文提出一种考虑配电系统接入大量电动汽车充电负荷后出现输电阻塞情况时的城市电动汽车充电站优化配置模型。该模型由上层决策模型和下层决策模型组成，上层模型以电动汽车制造企业的投资收益最大化为目标，考虑电网潮流、储能系统充放电和投资预算等约束条件；下层模型以电动汽车用户的满意程度最大化为目标，考虑用户选择充电站和充电站必须存在约束条件，并采用改进遗传算法对模型进行求解，进而确定充电站的最优规划方案。

1 电动汽车充电负荷计算

电动汽车充电负荷计算是概率性问题，将电池初始SOC与初始充电时刻、用户出行与驾驶习惯和充电电价等因素综合分析，可建立精确的电动汽车充电负荷计算模型，这是电动汽车充电设施网络建设的前提。本文主要考虑电动公交车、电动客车、电动出租车（网约车）和电动私家车，由于各类电动汽车出行规律各异，根据文献［8，10］中将电动公交车和客车归为一类，电动公交车、电动客车和电动出租车的日行驶距离满足正态分布［11］，电动私家车日行驶距离满足对数正态分布［3］，具体为：

式中：s表示电动汽车的日行驶距离；μ1和σ1表示电动公交车、电动客车与电动出租车的日行驶距离期望和标准差；μ2和σ2表示电动私家车的日行驶距离期望和标准差。

不同类型电动汽车的日行驶距离与充电时刻与用户的出行习惯息息相关，本文采用文献［12］中拟合结果描述电动汽车初始充电时刻的概率密度函数，即

式中：tb为电动汽车初始充电时刻；μ3和σ3分别为开始充电时刻的期望和标准差。

电动汽车充电时长与日行驶距离有关［12］，即

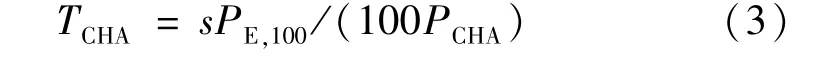
式中：PE，100为电动汽车行驶100 km 的耗电量；PCHA为充电功率。

2 节点边际电价模型

2.1 数学模型

LMP定义为电力系统实时运行状态下，某个节点负荷增加单位有功功率，并满足电网运行安全约束时系统边际成本［13］。在电力市场中，LMP表征了不同节点在不同时刻的电能价值，反映了电能的稀缺程度。

基于交流最优潮流的LMP模型，能精确反映电网的网络损耗和电网阻塞情况。交流最优潮流模型通常是以全网发电机组发电成本最小为目标函数，具体表达式为

式中：N表示全网节点数量；ɑi、bi和ci分别表示节点i处发电机组的发电成本函数系数。

需满足的约束条件包括节点功率平衡和线路潮流不越限，具体表达式为

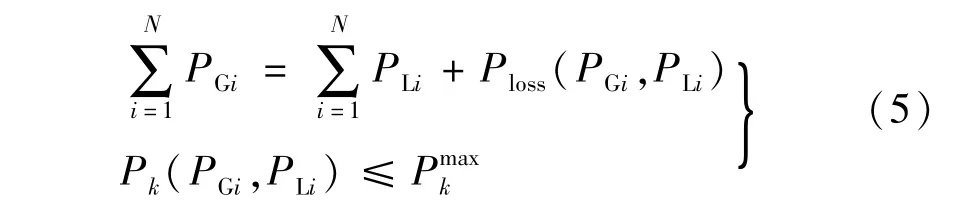
式中：PLi和Ploss分别表示节点i的负荷有功功率和系统网络损耗；Pk和分别表示线路k的实际有功功率和有功功率最大值。

2.2 含电动汽车充电站的节点边际电价模型

电动汽车充电站通过节点接入配网，在功率平衡等式约束条件中加入充电负荷变量PCi即可构成含电动汽车充电站的节点边际电价模型。将目标函数和约束条件形成拉格朗日函数L，具体表达式为

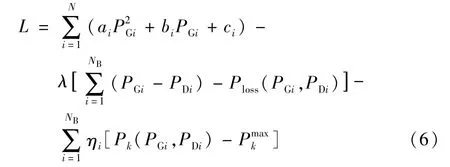
式中：PDi表示节点i处接入充电站后的节点负荷有功功率，PDi=PLi+PCi；λ 和η 分别表示各约束条件对应的拉格朗日乘子。

根据KKT一阶最优条件，即可求得节点i处的节点边际电价的表达式为

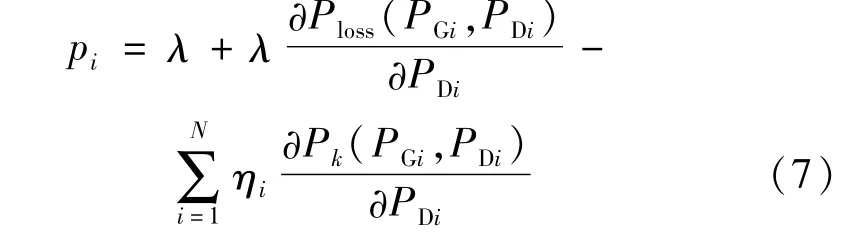
由式（7）可知，LMP是一个非线性函数，由能量价格分量、网络损耗分量和线路阻塞分量构成。当电网不发生网络阻塞时线路阻塞分量为零。因此，在进行电动汽车充电站规划设计时需重点考虑。

3 充电站双层规划模型及求解

电动汽车生产企业（如特斯拉、蔚来、吉利和比亚迪等）和充电设施制造企业（如特来电、许继电气和上海普天等）为增加自家电动汽车或者充电设施的市场占有率，会在城市中构建自己的电动汽车充电服务网络。本文以电动汽车生产或制造企业为对象进行研究，此类投资者侧重于电动汽车充电服务网络产生的收益和用户服务满意度。

3.1 上层规划模型

随着电池技术的日益成熟，电动汽车的数量逐年攀升，尤其是一二线城市，未来三四线城市的增长率也会越来越大。因此，上层决策者会根据城市的电动汽车保有量、城市配电系统和城市道路交通网络等多维度信息，并充分考虑电动汽车充电站的总投资预算、充电容量和电压安全等约束条件，以充电站的年收益最大为目标建立上层规划模型，即

式中：CBEN、CINC和CCOS分别表示投资充电站而获得的总投资收益、总营业收入和总投资成本；r和τ分别表示年利率和充电站运行年限。

（1）总营业收入CINC。总营业收入是指投资者通过运营电动汽车充电站而获得的总营业收入，主要包括充电营业收入、提高分布式电源设备利用率收益和削峰填谷政府补贴收入，具体表达式为

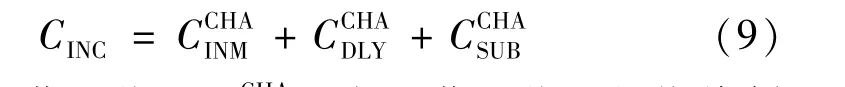
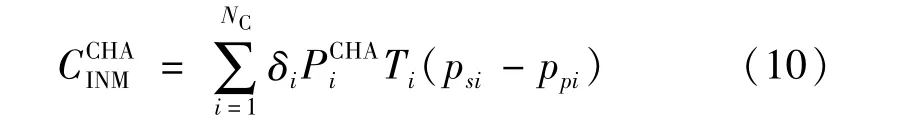
式中：NC表示新建充电站的数量；δi表示节点i处是否建设充电站的二元决策变量，值为1 表示新建，值为0 表示不新建；表示节点i处充电站的规划充电容量；Ti表示节点i处充电站的年最大利用小时数；psi和ppi分别表示节点i处充电站向充电用户售电价格和向电力公司购电价格，而购电价格就是前文所述的节点边际电价。

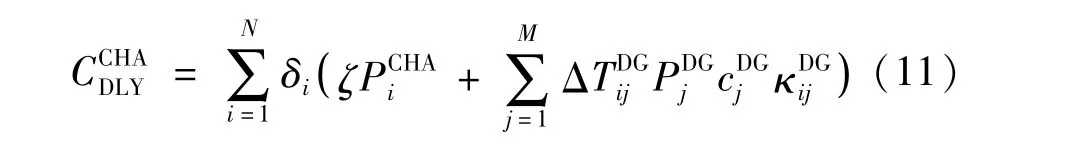
式中：ζ表示单位功率配网扩建成本；M表示配网中分布式电源的数量；表示节点i处电动汽车充电站提高了第j个分布式电源的年利用小时数；表示第j个分布式电源额定功率；表示第j个分布式电源平均套利电价；κ表示节点i处电动汽车充电站与第j个分布式电源投资商的分成比例。

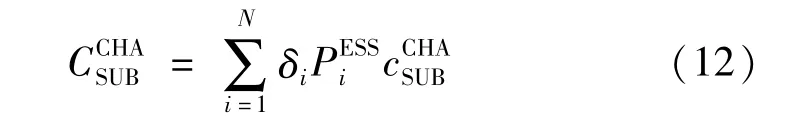
（2）总投资成本CCOS。电动汽车充电站的总投资成本包含充电站的建设与运营成本、财务成本和用户排队时间成本。

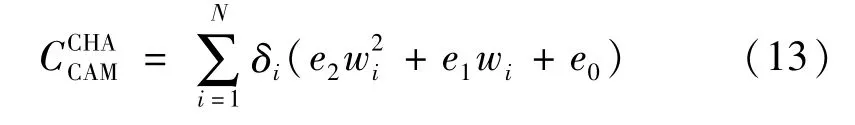
式中：wi为节点i处的充电站内充电机数量；e1和e2分别为充电机单价和与充电机台数有关的等效投资系数；e0为充电站固定成本。

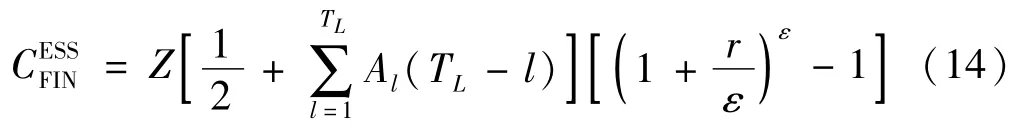
式中：Z表示项目贷款或融资的总额；TL表示充电站项目的建设周期；Al表示第l年的贷款资金使用比例，且满足；ε表示每年计息次数。

式中：M为充电用户数量；λmi为第m个用户选择节点i处充电站的二元变量，值为1 表示选择，值为0 表示不选择；tmi为第m个用户在节点i处充电站内充电等待时间，用排队论求得［17］；c0为单位时间成本。

投资者建设充电站的上层规划模型需要满足相关约束条件。

（1）所有充电站接入配电系统的总功率应小于配电网允许的最大接入功率，即

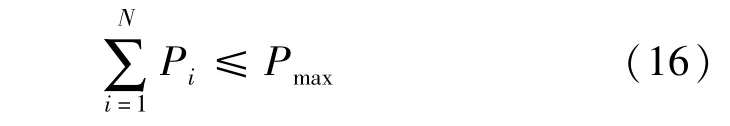
式中，Pmax表示配网允许的最大接入功率。

（2）为保证配电系统的安全稳定运行，充电站接入配网运行后，配网节点的电压幅值应满足响应的约束条件，即

式中：Ui表示城市配网节点i处电压幅值；分别表示节点i处电压幅值的最小值和最大值。

（3）配网线路极限容量固定，充电站接入配网后应保证馈线电流在规定范围内，即

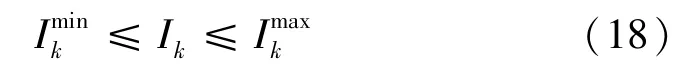
式中：Ik表示实际流过线路k的电流；分别表示流过线路k电流的最小值和最大值。

（4）充电站配置的储能系统充放电功率应满足相应约束条件，即

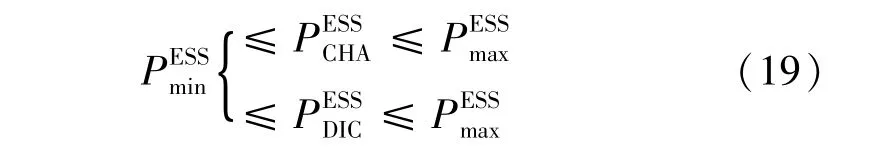
（5）企业投资者在进行项目时，会考虑到项目投资预算，即

式中，CINV表示项目总投资预算。

（6）根据规划区内电动汽车数量预测，企业投资者会制定新建充电站数量约束，即

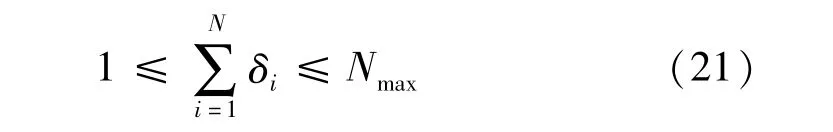
式中，Nmax表示新建数量上限。

3.2 下层规划模型

投资电动汽车充电站就是让电动汽车用户获得最大的体验感和满意度，充电服务时间是决定用户体验的关键。因此，本文引入效用函数［18］来衡量用户对充电服务时间的体验感和满意度ρ，其具体表达式为

据此，下层规划模型以用户体验感或满意度最大为目标，具体表达式为

下层模型需要满足的约束条件如下：

（1）用户只能选择一个电动汽车充电站进行充电服务，即需要满足的约束条件为

（2）第m个用户选择节点i处的电动汽车充电站进行充电的前提是节点i处存在充电站，因此，须满足的约束条件为

3.3 模型求解算法及流程

双层规划问题是一个NP-Hard 问题，采用智能算法进行求解可提高运行效率和精度。本文基于遗传算法［19］并结合所提模型的特点，进行相应改进和校验，进一步提升模型求解精度。电动汽车充电站双层规划模型的求解流程如图1 所示。

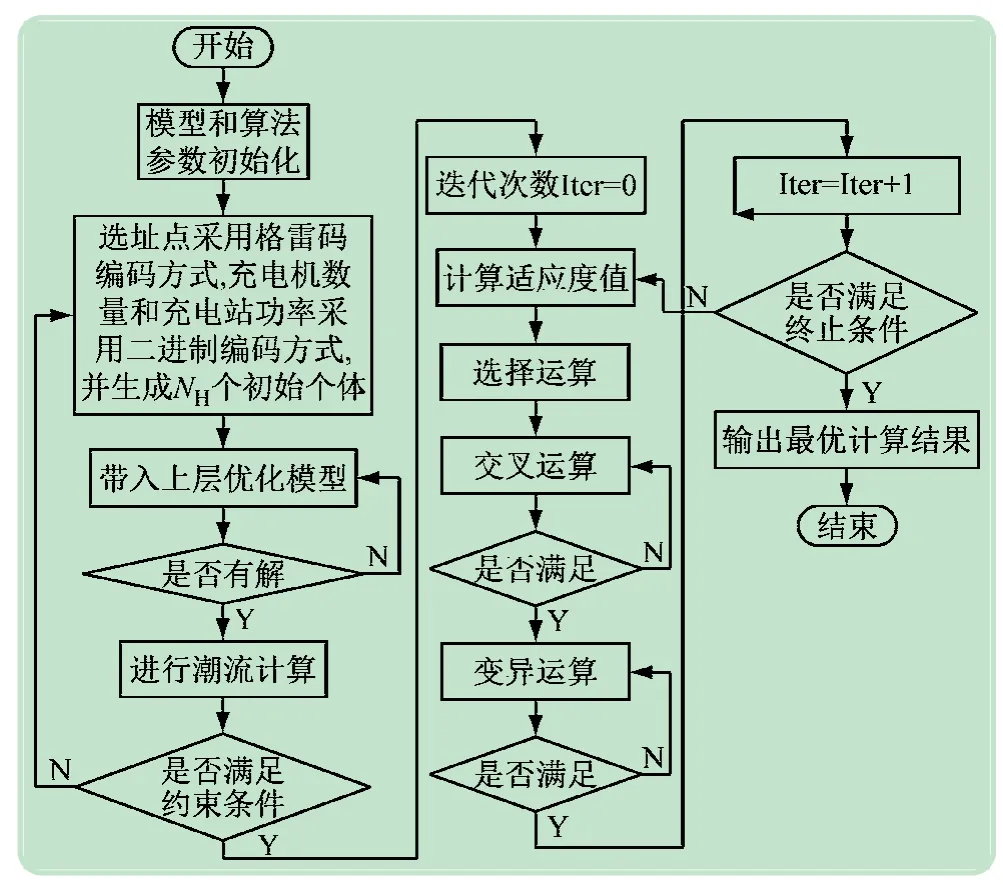
图1 双层规划模型的求解流程

4 算例分析

本文以中国西部某局部配网拓扑为算例，该局部配网覆盖区域面积约为450 km2，电动汽车保有量预测数据为10 万辆。该局部配网包括4 条10 kV 线路分别由4 座变电站引出，3 个线路联络开关，根据实际道路地理信息，所有电动汽车充电站备选点均位于道路的交叉路口，共计12 个，如图2 所示。配网中风力机组的额定功率为1.0 MW，光伏发电机组的额定功率为0.75 MW。根据电动汽车保有量和预测模型，该规划区域内单日充电功率的最大期望值是28.64 MW。某电动汽车制造商根据城市汽车保有量、交通和配网等信息，计划在该区域内投资新建5～8 座电动汽车充电站。

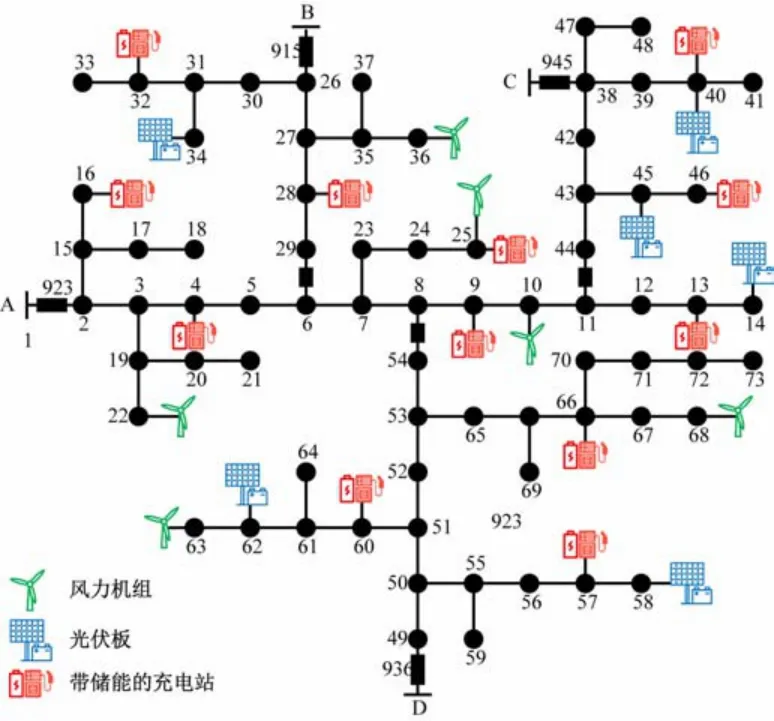
图2 规划区域电网拓扑

4.1 仿真结果分析

假设图2 中4 个变电站出线均正常运行，联络开关也处于闭合状态，充电站配置的储能系统在负荷曲线低谷时间充电一次，在白天负荷高峰时段放电一次，在MATLAB中编写程序，将所有参数信息带入本文所提模型中进行求解，规划区域内电动汽车充电站的最优规划方案如表1 所示。

表1 充电站最优规划方案

当变电站B 发生永久性故障时，馈电线路915 开关断开隔离，馈线915 的负荷由变电站A、C和D提供支撑。将各类参数带入所提模型，电动汽车充电站的最优规划模型如表2 所示。

表2 故障下充电站最优规划方案

上述两个场景（未发生和发生故障）对应的投资收益和投资成本的具体组成如图3 所示。

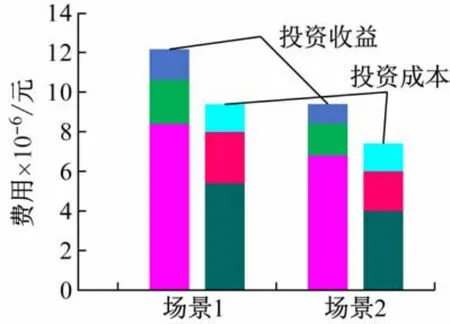
图3 投资收益和投资成本的具体组成

表3 为考虑配电系统阻塞情况下使用户满意度最大的最优规划方案。

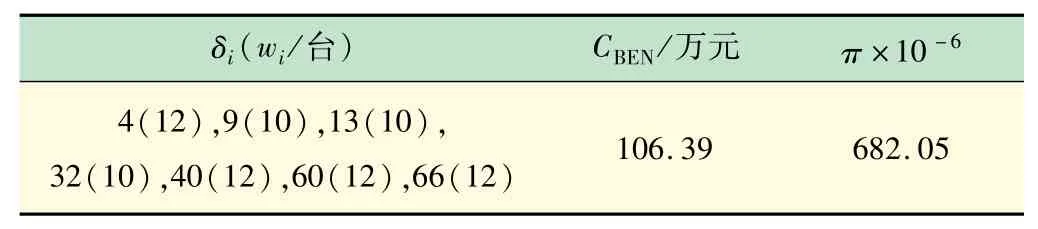
表3 故障下考虑阻塞时充电站最优规划方案

当配电系统发生故障时，考虑电网阻塞和不考虑电网阻塞的节点边际电价结果如图4 所示。

根据表1～3、图3 和4 可知，配电系统正常运行情况下，企业投资者不仅能获得更大的投资收益，还能增强电动汽车用户的充电体验感和满意度。但是，由图4 可知，当配电系统出现故障且暂时无法恢复时，由于线路容量的约束，会出现线路阻塞，节点边际电价就会发生变化，导致部分节点的充电电价被抬高，如节点13、节点25，即充电站向配电网购电的成本增加，则投资收益也随之降低（由192.97 万元降至106.39 万元）。

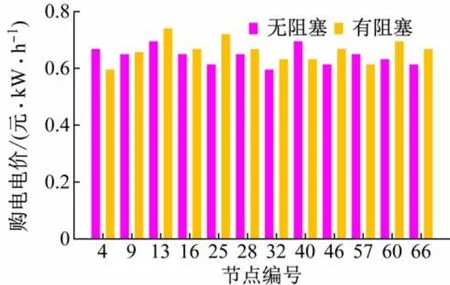
图4 充电站备选点对应节点的节点边际电价

然而，对于电动汽车制造企业而言，投资充电站的目的是吸引更多的消费者购买电动汽车，增加电动汽车销量，充电站的投资收益可忽略。因此，在充电站年总投资成本差异较小的情况下，增强用户体验感更能使投资者增加市场占有率（满意度由415.67 ×106增加至682.05 ×106）。

另外，由表2 和表3 可知，虽然电动汽车充电站的投资收益减少了44.86%，但是用户的满意度却提升了64.08%，即规划区域内电动汽车用户在充电站内节约了大量时间，有利于吸引更多的电动出租车和电动网约车用户来充电，也会刺激更多的消费者购买投资商的电动汽车或者充电设施。

综上所述，随着电力改革逐步深入，电动汽车充电站的运营公司可作为购电用户参与市场化交易，电网阻塞对节点边际电价的影响会越来越大，投资者需重点考虑该影响因素。

4.2 规划方案参数特性分析

（1）储能运行策略。电动汽车充电站所配置的储能系统是在电网低谷时段对储能充电，在负荷高峰时放电为电动汽车充电，不仅能响应电网公司的需求侧管理，降低电网运行风险，而且能利用电价价差套利。但储能系统投资成本较高，容量有限，充一次电不能满足电动汽车充电站1 d 的放电运行，储能系统不同充放电次数下充电站规划方案如表4 所示。

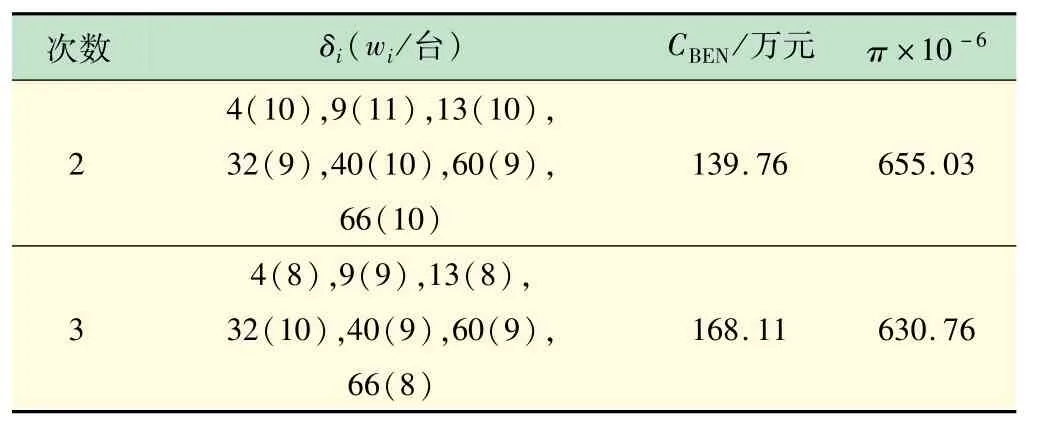
表4 储能系统不同放电次数下充电站最优方案

从表4 可知，储能系统在1 d 内的充放电次数不同会影响电动汽车充电站站内充电机数量，投资收益略微提升，因为投资成本减少了。充电用户满意度略微下降，由于充电机数量减少了，等待时间略微延长，但总体效果还是可以保证。

（2）电动汽车渗透率。电动汽车制造企业投资运营电动汽车充电站多为了吸引消费者购买电动汽车，则应考虑电动汽车保有量逐渐增加，充电负荷需求增加，假设电动汽车保有量在前文的基础上再增加50%，在模型其他参数不变的情况下，对所提方法进行求解，充电站最优规划方案如表5 所示。

表5 故障下不同渗透率时充电站最优方案

从表5 可以看出，为了满足更多电动汽车充电用户的需求，电动汽车充电站的充电机数量增加，使用户等待时间降低，客户体验感和满意度都得到了大幅度提升。虽然投资收益增长较小，但为吸引更多消费者和保证电动汽车用户不流失，构建完善的充电服务网络对投资企业很有优势。不仅如此，完整的充电服务网络还能吸引其他电动汽车品牌的用户。