双树复小波与双变量阈值模型的图像去噪

左文涛，陈家益

（1.广州工商学院工学院，广州 510850；2.广东医科大学信息工程学院，广东湛江 524023）

0 引言

高斯噪声是图像中的一种常见噪声，产生于图像的拍摄、传输与处理中，是一种加性噪声，相对于其他噪声，高斯噪声的去除难度较大。目前去除高斯噪声的主要方法有小波阈值去噪法［1］和双树复小波变换去噪法［2］。因为多分辨率分析和信号局部特征表示的能力，小波变换广泛应用于图像处理。最初，学者们提出了小波阈值去噪法［3］，但是缺乏图像细节保持和噪声分离的能力。于是，文献［4］将噪声检测引入到小波阈值去噪中，且利用边缘检测对小波阈值进行增强。为了克服小波阈值滤波在去噪性能和计算速度上的不足，Elaiyaraja等［5］提出了一种去除医学图像中高斯噪声的小波阈值优化方法。为了进一步改进小波变换的性能，Wang等［6］提出三维小波的定义，三维小波具有良好的噪声系数表示能力。Ozmen等［7］充分利用三维小波，提出了基于体积子频带加权原理的加权三维小波去噪算法，子带加权旨在更好地改善图像表示能力以及自适应地去除图像中的噪声。

尽管小波变换是一种优秀的图像处理与分析工具，但是其平移敏感性和缺乏方向选择性严重制约了性能的发挥，因此Selesnick等［8］提出了双树复小波变换（DTCWT）的框架。双树复小波变换克服了小波变换的缺陷，还具有平移不变性和多方向选择性，能更有效地表达图像的特征。张丽娟［9］提出了双树复小波变换域的矿区遥感图像滤波方法，在复小波域中结合多级中值滤波以去除因成像环境和成像固件缺陷引入的噪声。殷明等［10］提出了将双变量统计模型引入到双树复小波变换的实部和虚部系数中，将实部和虚部系数的联合概率模型作为去除高斯噪声的数学模型。Vijayaraghavan等［11］将非抽样的小波变换与双树复小波变换结合，以产生非抽样的双树复小波变换，从而提供改进的低尺度子带定位和改进的方向选择性，以更好地去除高斯噪声。Laavanya 等［12］提出了一种结合奇异值分解和Frobenius 能量校正因子的双树复小波变换，并利用二元收缩函数对图像进行阈值化处理（SVDBL）。但是Frobenius 能量校正因子缺乏理论基础，难以适用于不同图像，鲁棒性较差。Hazarathaiah等［13］对Kingsbury和Selesnick 的DTCWT 滤波器进行改进，提出了整数DTCWT滤波器，降低了方法所依赖的硬件复杂度，同时具备DTCWT 平移不变性和多方向选择性等优点。但是其不足在于降低了图像系数的表示精度，忽略了图像的细微特征。

为了充分利用双树复小波变换的优秀特性，有效地保持和恢复图像的边缘和细节，本文提出了基于双树复小波与双变量阈值去噪模型的图像去噪方法。用双树复小波对图像进行变换，用基于贝叶斯估计的双变量阈值去噪模型对图像系数进行去噪处理。

1 双树复小波变换

双树复小波变换建立于小波理论基础上。复数小波表示为

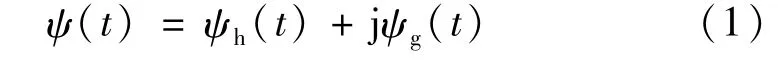
式中，ψh（t）和jψg（t）分别表示复小波的实数与虚数部分。

双树复小波变换是由两组实数小波变换实现的复数小波变换，通过两组并行的实数小波滤波器组实现。采用具有相互平行关系的实数小波二叉树结构，一棵树生成复小波系数的实部；另一棵树生成复小波系数的虚部。双树复小波变换的分析滤波器组见图1。

图1 双树复小波变换的分析滤波器组

图中：h0（n）和h1（n）分别表示共轭正交滤波器对；g0（n）和g1（n）表示共轭积分滤波器对；↓2 表示隔点采样。二维双树复小波变换通过一维变换的张量积获得，它是可分离实现的变换，先对每行，再对每列进行一维的双树复小波变换。对于可分离的二维小波变换，小波函数ψ（x，y）表示为

双树复小波实部和虚部的方向以及幅值的特征如图2 所示，其中第1 行为复小波实部的方向；第2 行为复小波虚部的方向；第3 行为复小波的幅值。双树复小波变换继承了小波变换的多分辨率分析等优良特性，同时克服了小波变换的缺陷，具有多方向选择性（见图2）和平移不变性（见图3）等优点。

图2 双树复小波的方向和幅值

图3 双树复小波与小波变换对阶跌信号的变换

2 贝叶斯估计的双变量阈值模型

高斯噪声为加性噪声，服从零均值的高斯分布，经双树复小波变换后，在小波域的数学模型为

噪声系数n服从零均值的高斯分布

为了充分利用小波系数在尺度间的相关性，令y1=w1+n1为当前尺度的小波系数；y2=w2+n2为下一尺度的小波系数，从而有：

式中：Y=（y1，y2），W=（w1，w2），N=（n1，n2）。图像去噪就是根据含噪的小波系数Y得到尽可能准确的原图像W的估计值。根据式（4），运用最大后验概率估计可得：

从被动接受厂商条款到主动寻求需方权益，从断档管理到医学装备的全生命周期管理，从单一医疗机构实践到行业协会共同推行，这是省医院以“大型进口医疗设备维保服务规范化招标采购”案例为突破口，带动整个地区医疗机构现代医院管理升级的典型路径。

运用贝叶斯估计方法可得：

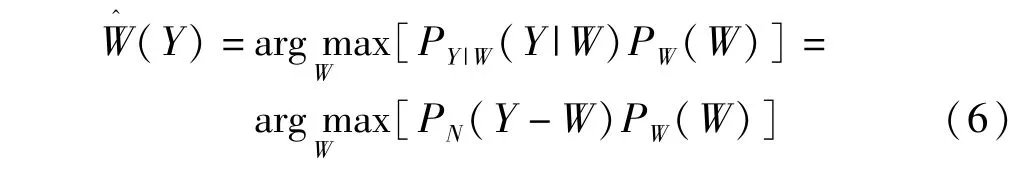
为了便于计算，上式等价于

假设噪声n为独立同分布，有

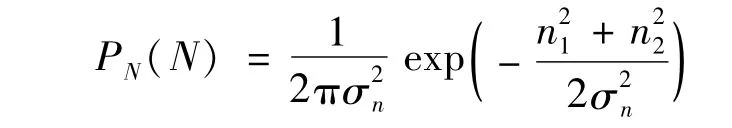
W可看作近似服从联合拉普拉斯分布

于是，式（7）等价于

上式的自变量为w1和w2，根据二元函数的导数求极值的方法，上式等价于求解：

从而原图像系数w1的估计值为

式中：σw为原图像w的标准差，表达式为阈值，自适应于图像和噪声的特征值。根据Donoho等［14］提出的鲁棒中值估计方法对σn进行估计

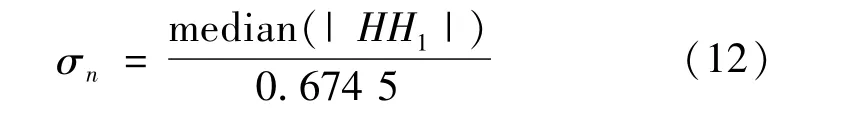
令σy为含噪图像y的标准差，其可由下式得到：

式中，M×N为图像的大小。对于式（3）的加性高斯噪声模型，有，因此，原图像w的标准差为

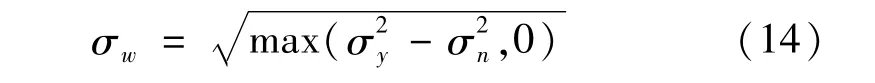
3 实验分析

以处理器为Intel（R）Core（TM）i9-10900@2.80 GHz，内存为32 GB 的计算机和Matlab 2019a 为实验平台，以文献［4，7，11，12］中的方法为参照，根据图像的视觉感知、峰值信噪比（PSNR）和边缘保持指数（EPI）［15］分析所提出方法的效果。实验所用的数据集为BSD68 和部分医学图像，其中医学图像如图4所示。

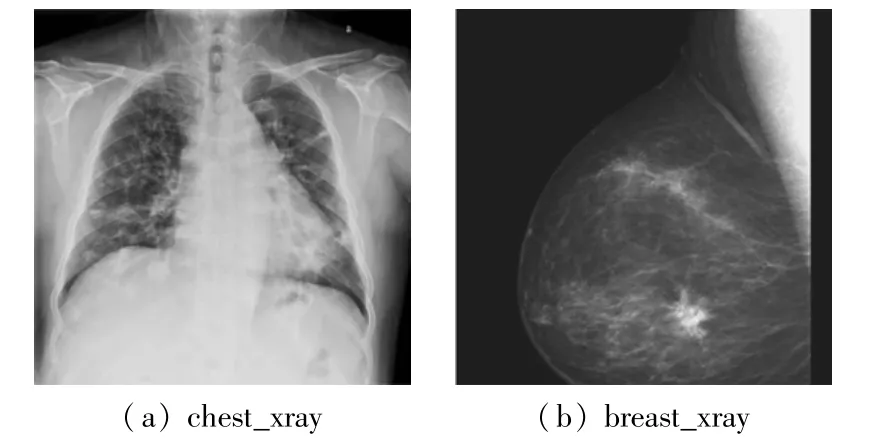
图4 医学图像

3.1 去噪图像

对含噪强度σ=35 的乳腺图像breast_xray，各算法的去噪处理图像如图5 所示，各分图下的两个数字为对应的PSNR 和EPI 值。与原图像相比，含噪图像的前景和背景都充满噪声斑点。文献［4］中的方法明显地去噪不彻底，从前景的目标可以看出来，噪声依然存在。从去噪图像目标轮廓以及纹理细节可以看出，文献［7，12］中方法的模糊效果严重。文献［11］中方法和本文方法的去噪效果较好，彻底去除了噪声，同时较好地保持了图像的边缘和细节。但对图5（d）和（f）作进一步仔细的观察，本文方法好于文献［11］中的方法，比如乳腺的轮廓，其边缘线条更加丰富和细腻。另外，根据各分图的PSNR 和EPI 值同样可以得出与以上一致的结论。

图5 乳腺图像breast_xray的去噪图像

3.2 去噪的客观效果

将各算法应用于含不同强度噪声的数据集BSD68得到的PSNR 和EPI 曲线如图6 所示。从PSNR 和EPI曲线的高低和走势可以看出，文献［7，11］中的去噪效果较差，PSNR 和EPI 曲线的走势均处于较低位置。在噪声强度较低时；文献［4］中的性能表现还可以接受，但是随着噪声强度的提高，其性能骤然走低。由文献［12］中PSNR 和EPI 曲线可以看出，该方法的去噪效果较好。相对地，本文方法的性能表现相对现有方法拉开一定的差距，相对于性能较好的文献［12］的方法，本文方法的PSNR 高出约6 dB，EPI 高出约10%，特别地，在噪声强度较高时，本文方法的边缘保持能力更加显著。

图6 各算法对数据集BSD68去噪的PSNR和EPI

对医学图像chest_xray 的去噪结果如图7 所示。总体上，文献［7，4］中方法的性能较差，虽然在噪声强度较低时，文献［4］中方法的PSNR 值较高。文献［11］中的方法在去噪性能和边缘保持能力上处于中等水平，但是在噪声强度较高时，其边缘保持能力较差。文献［12］中方法的PSNR 和EPI 值较高，总体上性能较好。相对地，本文方法在去噪性能和边缘保持上均为最优，相比性能较好的文献［12］，本文方法的PSNR高出大约0.9 dB，EPI高出大约3.2%。

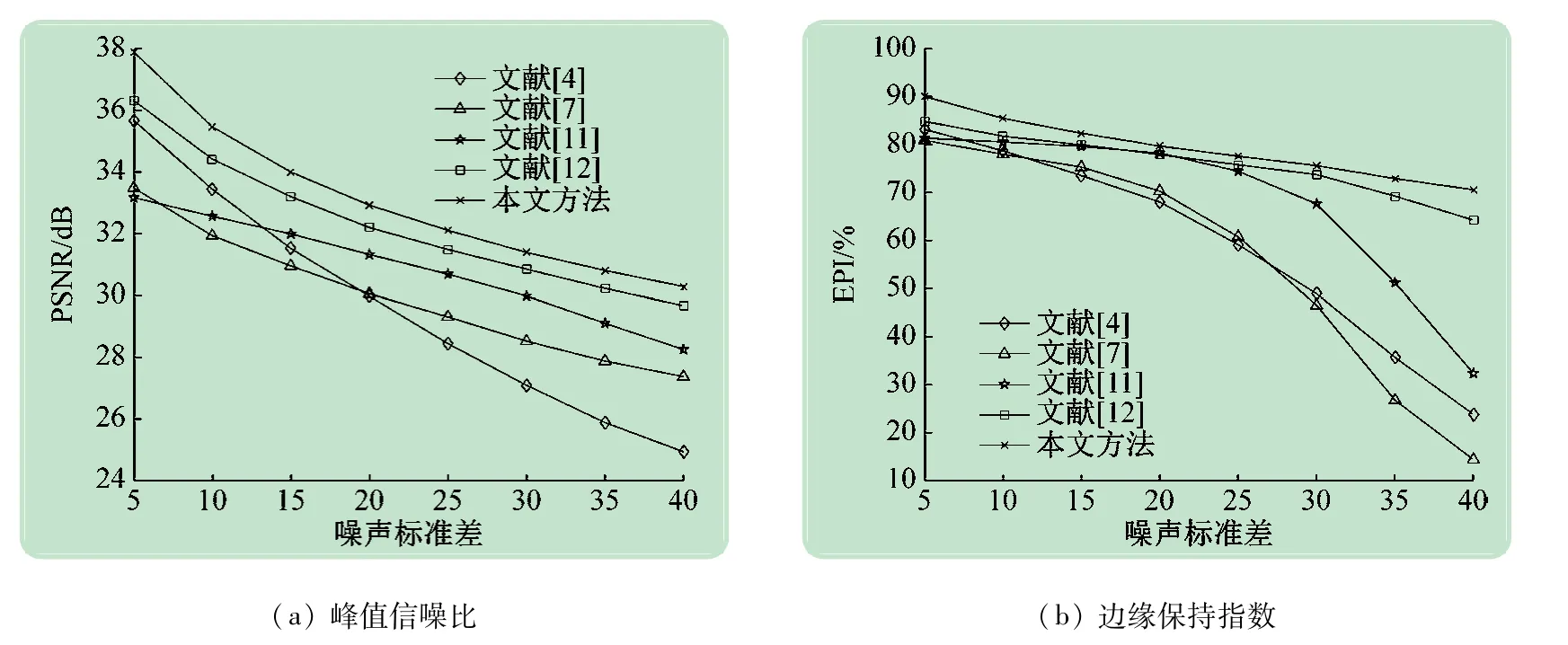
图7 各算法对医学图像chest_xray去噪的PSNR和EPI

综上，从视觉感知和客观的图像质量指标可以看出，所提出的方法具有更好的去噪性能以及边缘保持和恢复的能力。对于性质不同的图像，其始终取得比现有方法更好的去噪效果，具有良好的鲁棒性。

4 结语

为了进一步提升高斯噪声的去除效果，提出了基于双树复小波与双变量阈值模型的去噪方法。为更好地保持图像的细节和纹理，充分利用双树复小波变换的平移不变性和多方向选择性，将双树复小波变换用于图像的分解。然后根据对图像和噪声的分布假设，由贝叶斯估计推导出基于双树复小波变换的双变量阈值去噪模型，以去除噪声。实验数据证明了所提出方法的有效性，具有良好的去噪性能以及边缘保持和恢复的能力。将方法作进一步的改进，以适用于混合噪声，是本文下一步的研究工作。

全面提高高等教育质量。高等教育承担着培养高级专门人才、发展科学技术文化、促进现代化建设的重大任务。提高质量是高等教育发展的核心任务，是建设高等教育强国的基本要求。到2020 年，高等教育结构更加合理，特色更加鲜明，人才培养、科学研究和社会服务整体水平全面提升，建成一批国际知名、有特色高水平高等学校，若干所大学达到或接近世界一流大学水平，高等教育国际竞争力显著增强。

——摘自《国家中长期教育改革和发展规划纲要》