永磁同步电动机高性能位置控制实验研究
2021-12-14程国扬余文涛
程国扬,余文涛
(福州大学电气工程与自动化学院,福州 350108)
0 引言
大学工程教育的一个关键问题是培养学生的实践与创新能力,这促使大学教师要不断优化课程体系、加强实验环节的训练[1-4]。与此同时,大量的工作也投入到各种典型实验案例的设计和实训平台的研制[5-9],为工程技术人才的培养提供必要的保障。近年来,把科研与教学相结合,特别是把学科领域的前沿技术融入到实验训练中[10-11],使学生的知识和技能更好地适应社会需求,是一个发展趋势。
在工业加工和装配自动化系统中,广泛采用永磁同步交流电动机作为传动机构构成高性能伺服系统。这类系统需要完成快速、平稳与准确的大范围点位运动控制,以满足生产效率和产品精度的要求。因此,研发高性能伺服控制技术具有重要的现实意义[12]。实际上,这也是电力传动与控制领域的研究热点之一;另一方面,在大学的自动化、电气工程(电力传动方向)专业的培养计划中,都把以永磁同步电动机(Permanent Magnet Synchronous Motor,PMSM)为核心的交流伺服系统列为必修课程,并设置了相应的实验(实训)环节。传统上,交流伺服系统采用电流-速度-位置三环串级控制的模式,并采用比例-积分-微分(PID)之类的简单控制律进行闭环控制。这种方案虽然可行,但不容易得到理想的控制性能。为了让学生更好地掌握电动机伺服控制方法,在实验教学中引入本领域的一些先进理念和研究成果,比如采用机械运动外环(由电动机转速-位置构成)与电流内环的双环结构,其中内环由于需要高的离散采样频率、适于采用简单控制律,而外环所需的采样频率不高,可以采用一些稍微复杂的控制算法,来实现期望的伺服性能。
虽然现有大量的研究文献介绍了各种先进伺服控制技术,但要把它们应用到实验教学中并不容易。任课教师在把先进技术引入实验教学的过程中面临着知识瓶颈与实验技能的双重挑战。在PMSM 伺服系统的实验教学案例设计中,针对高性能位置控制问题引入了两种先进控制技术。第1 种是目前在控制领域中非常流行的自抗扰控制(Active Disturbance-Rejection Control,ADRC))技术。这是由韩京清教授[13]首先提出的,经过20 多年的研究与发展,目前已有大量成功的应用,有望成为替代PID 的工业控制方案。第2 种控制技术是所谓的鲁棒快速伺服控制技术,它以近似时间最优伺服(Proximate Time-optimal Servo,PTOS)控制为基础[14],即在初始阶段采用时间最优控制律进行系统加速,而当系统误差进入预期范围内则改用线性控制律实现平稳控制;当系统运行速度超出允许值时,则插入一个恒速调节阶段,通过切换控制实现大范围位置控制[15]。
本文对PMSM 位置伺服控制实验案例的具体设计为,通过MATLAB 仿真和基于TMS320F28335 数字信号处理器的实验研究,展示其应用方法和控制效果。
1 PMSM的数学模型及控制框架
高性能伺服系统通常采用PMSM 作为驱动机构,其在dq坐标系下的数学模型为:
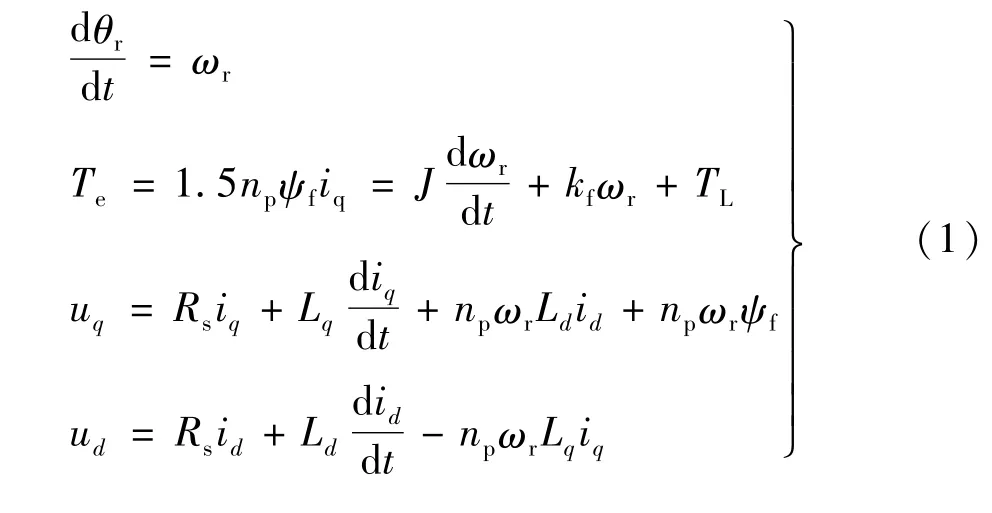
式中:θr为电动机的机械转角(rad);ωr为机械角速度(rad/s);Te为电磁转矩(N·m);TL为负载转矩(N·m);J为电动机的惯量(kg·m2);kf为黏性摩擦系数(N·m·s/rad);ud、uq分别是三相电压矢量在直轴(d轴)和交轴(q轴)的分量;id、iq为励磁电流和转矩电流;Ld、Lq为电动机直轴和交轴同步电感;Rs为定子电阻;np为极对数;ψf为永磁体磁链。
采用基于=0 和SVPWM(Space Vector PWM)的磁场定向矢量控制方案。如图1 所示,系统采用双环控制结构,其中电流环已通过抗饱和PI控制律进行调节,实现了内部闭环。考虑由电动机速度和位置构成的机械子系统,若以转角θr作为系统的受控输出量,iq作为控制输入量u(内环的电流命令),并把黏性摩擦(其值比较小)和负载转矩都归入扰动,则可得到机械运动子系统的数学模型如下:

图1 PMSM位置伺服控制系统结构
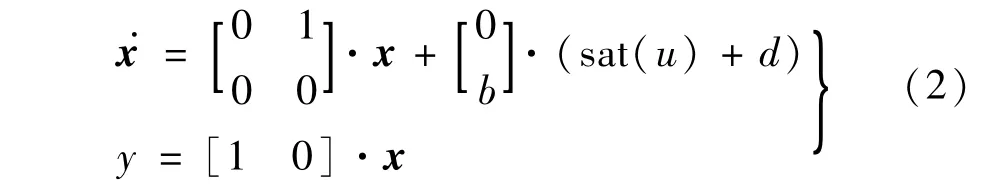
式中:状态向量

包含位置和速度信号;y=θr是可量测的被控输出位置量;u=iq是控制输入量;代表由负载扰动和其他不确定因素折合而成的等价输入扰动(未知);b=1.5npΨf/J>0 为系统参数。考虑到实际系统物理量的限制,引入饱和限幅函数sat(·),定义如下:

式中:umax是控制量的饱和限幅值,这里是最大的转矩电流值;sign(·)是标准的符号函数。针对模型式(2),需要设计位置伺服控制律,对电动机位置进行调节。
2 位置伺服控制律设计
2.1 自抗扰控制
自抗扰控制(ADRC)的出发点是为线性和非线性不确定系统提供一种统一有效的控制方案,它对系统模型做了大胆的简化假设,即控制器的设计只需用到系统的相对阶和增益系数,而把模型的其他项和外部干扰都归入一个总扰动(扩展的状态变量)。利用非线性观测器提供对状态和扰动的在线估计,用于反馈补偿;利用非线性误差反馈律来提高控制性能;必要时,可引入微分跟踪器(或滤波器)来安排瞬态过程。
针对式(2)的系统,设计一个自抗扰控制器如下:

式中:β1,β2,α1,α2,δ是正参数;fd∈[0,1]是扰动补偿的折扣系数增益,可用于在系统稳态精度与鲁棒性(对测量噪声的敏感性)之间折中(应该指出,这一系数在ADRC文献中并未出现,这里引入它是为了提高控制律的灵活性,使得控制实验更容易进行);非线性函数fal(·)定义如下:

式中:e1=rf-z1;e2=·-z2=-z2,其中rf是给定信号r(阶跃信号)经过一个滤波器后的输出信号。该滤波器用于安排过渡过程,其传递函数如下:
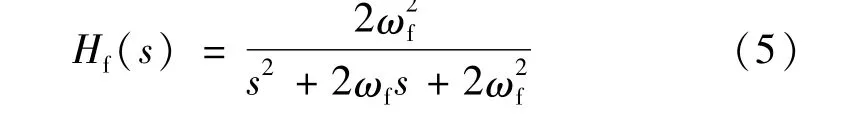
式中,ωf>0 与滤波器带宽有关。
前面公式中变量z1、z2和z3是以下非线性扩展状态观测器(Nonlinear Extended State Observer,NESO)的状态量:
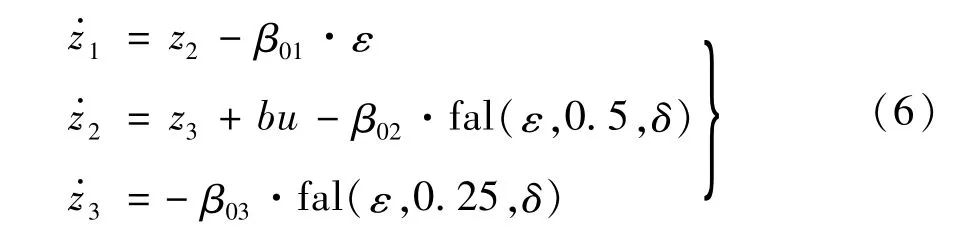
式中:ε=z1-y;β01,β02,β03是下一步要确定的观测器增益(正标量)。自抗扰控制器的参数整定通常比较困难。这里参照本领域的研究人员提出的一些常用的规则[16],对ADRC 的主要参数采用以下方法进行选择:

式中:ωc为控制器带宽;ζc∈(0,1]为阻尼系数;ωo为观测器带宽。
实验中,控制律中的滤波器和观测器都需要经过离散化后才能编程实现。假定离散采样周期为Ts,采用后向差分离散化方法,得到式(5)滤波器对应的差分方程如下:


式(6)的NESO转换成离散形式如下:

在仿真和实验中,利用δ、α1、α2、ζc、ωc、ωo、ωf和fd作为可调参数,整定控制系统的性能。图2 给出了系统的示意图。
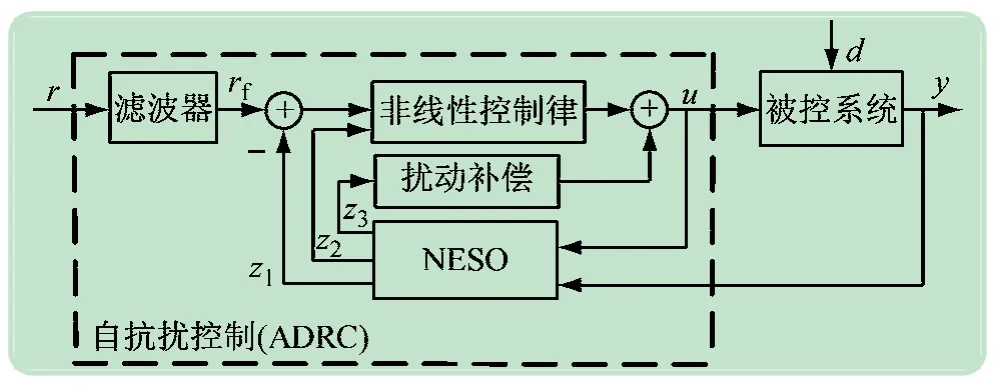
图2 ADRC的结构示意图
2.2 鲁棒快速伺服控制
式(2)的双积分伺服系统可简写成如下形式:
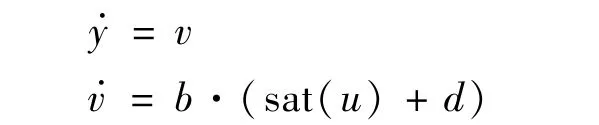
式中:y和v分别为系统的转角位置θr(输出量,可量侧)和转速ωr(未量测);d是未知的输入扰动;u为最大幅值为umax的控制量。
在控制量饱和限幅的条件下,可设计一个时间最优控制律(TOC)来对一个定点目标r进行快速跟踪。但它是一种Bang-bang 控制律,对微小的偏差量非常敏感,系统中的模型差异(包括未知扰动)或者测量噪声,都可能导致控制信号在正负两个极端值之间频繁切换,产生所谓的颤振(Chattering)现象。文献[14]在TOC控制律框架下引入一个线性工作区,即当误差的幅值较小时把TOC 控制律平滑地切换为线性控制。这种改进的控制方法就是近似时间最优伺服控制(PTOS),其控制律如下:
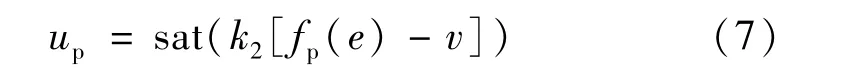
式中:e=r-y是跟踪误差;
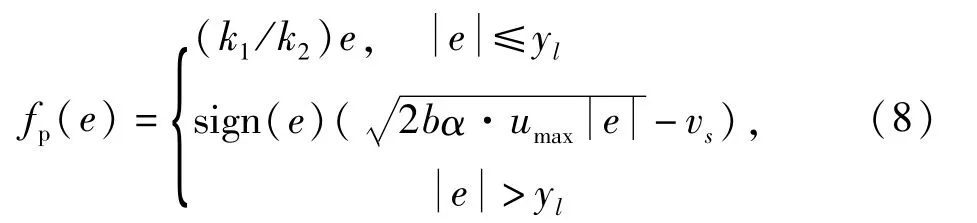
式中:k1和k2分别是位置和速度反馈增益;α 是加速度折扣系数,0 <α≤1;yl是线性工作区的宽度;vs是待定的偏置量;sign()是符号函数;fp(e)函数须满足连续性和平滑性的约束条件。
采用线性控制区的闭环极点阻尼系数ζ和自然频率ω作为设计参数,则PTOS 控制律其他参数可按下式推算:

控制律式(7)中用到未量测的速度信号v,而且也未考虑对扰动进行补偿,因而在实际应用中并不适用。假定系统的扰动是分段定常或慢变化的,则可用微分方程描述为=0。把该方程结合到对象模型中,得到增广后的模型为

注意到输出量y是可量测的,只需估计状态v和扰动d的值,因而可设计如下线性降阶观测器[15]:

式中:η是观测器的内部状态向量;ζ0∈(0,1]和ω0>0 分别是观测器极点的阻尼系数与自然频率。
把估计出来的状态变量用于PTOS 控制律,并考虑扰动补偿,得到最终的鲁棒伺服控制律如下:

式中,fd的作用与式(3)的相同。式(8)~(10)构成完整的控制律。
式(10)的控制律在进行定位控制时,先从静止状态开始加速,等到运行的距离和速度都到达一定值时,系统开始减速,当速度降为零时,被控对象也恰好到达指定的目标位置。因此,其对应的速度曲线近似为三角波,在这个三角波的顶点处,也就是加速段和减速段的转折点,速度达到一个最大值,而且定位目标越远,速度的最大值也会随着一起增大。考虑到实际系统对运行速度通常会有限制(速度太快,容易引发机械谐振,导致系统硬件故障),在进行大目标定位控制时,需要在鲁棒快速伺服控制的框架中插入一个恒速控制环节,当系统当前速度达到最大限速值(即),且PTOS控制量=sat(k2[fp(e)-])与当前速度方向相同(即>0),此时立即切换为恒速控制律,使系统运行在限速值的附近,而后随着系统接近目标位置使得PTOS 控制量与当前速度方向相反(即<0),则又切换回鲁棒伺服控制律(10)进行减速控制,直到被控对象到达目标位置,如图3 所示。采用这种三阶段切换控制方式,系统在大行程目标定位时的速度曲线将呈现为一个近似梯形波。若给定目标幅值较小,则系统的速度可能达不到限速值,控制器将直接从加速段进入减速段,最终的速度曲线仍是近似的三角波。
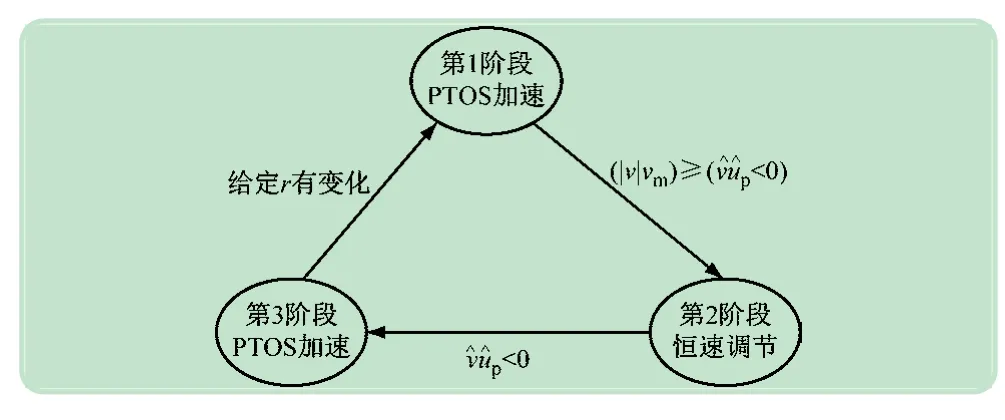
图3 速度受限鲁棒快速伺服控制的切换逻辑
恒速调节阶段采用比例控制+扰动补偿控制律:

式中:kv>0 是比例控制系数;vm是系统的速度限制值(即系统速度不能偏离该值太远),其前面带有符号函数是因为需要考虑进行双向运动定位控制的情况。
鲁棒快速伺服控制器的可调参数包括:线性区阻尼ζ(通常取0.8,保证低超调)和自然频率ω(与带宽有关),加速度折扣系数α(取值0.95 左右,根据系统模型的准确度进行调整),观测器参数ζ0(取值0.7~1.0)和ω0(可选为3ω 左右),扰动补偿系数fd(通常取值0.9~1.0),以及速度控制增益kv>0。限速值vm则根据实际系统进行适当选择。在实验中,观测器式(9)也要离散化,可参照ADRC 中的NESO 离散化方法,这里不再赘述。
3 Matlab仿真
仿真的目的是快速检验控制律的正确性,并指导控制律参数值的选择。这里仅考虑PMSM 伺服系统的机械运动子系统,即式(2)所描述的系统。经系统辨识,模型参数b=1 920。根据电动机的物理参数,确定umax=1.5 A。扰动d的范围是0~-0.8 A。
首先在给定r=π和扰动d=-0.4 A(相当于半载)情况下进行参数整定,使得两种控制律取得相近的满意性能,所得的参数值如表1 所示。然后保持参数值不变,但改变位置给定或扰动,测试控制效果。图4 展示了ADRC在半载情况下对3 种目标角度的定位控制仿真结果,图5 给出了ADRC在目标角度6π和3种不同负载(其中满载时,d=-0.8 A)下的仿真结果。可以看出,ADRC 在各种给定或负载下都能实现准确的位置控制,说明抗扰动能力较好。图6 是鲁棒快速伺服控制在3 种目标角度和半载下的仿真结果,图7 是其在目标4π和3 种负载下的仿真结果。虽然随着负载的加大,系统的响应有减慢的趋势,但总体性能仍旧保持良好。图8 显示了鲁棒快速伺服控制在目标角度6π、半载和3 种限速情况下的仿真结果,显然,当速度限值起作用时,系统速度波形出现了近似梯形波,而且随着限速值的降低,系统位置响应变慢。
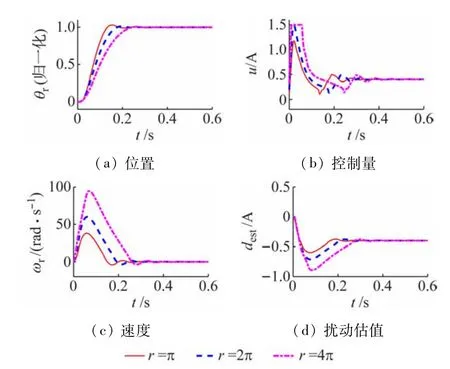
图4 3种目标角度和半载下自抗扰控制的仿真结果

图5 目标角度6π和3种负载下自抗扰控制的仿真结果
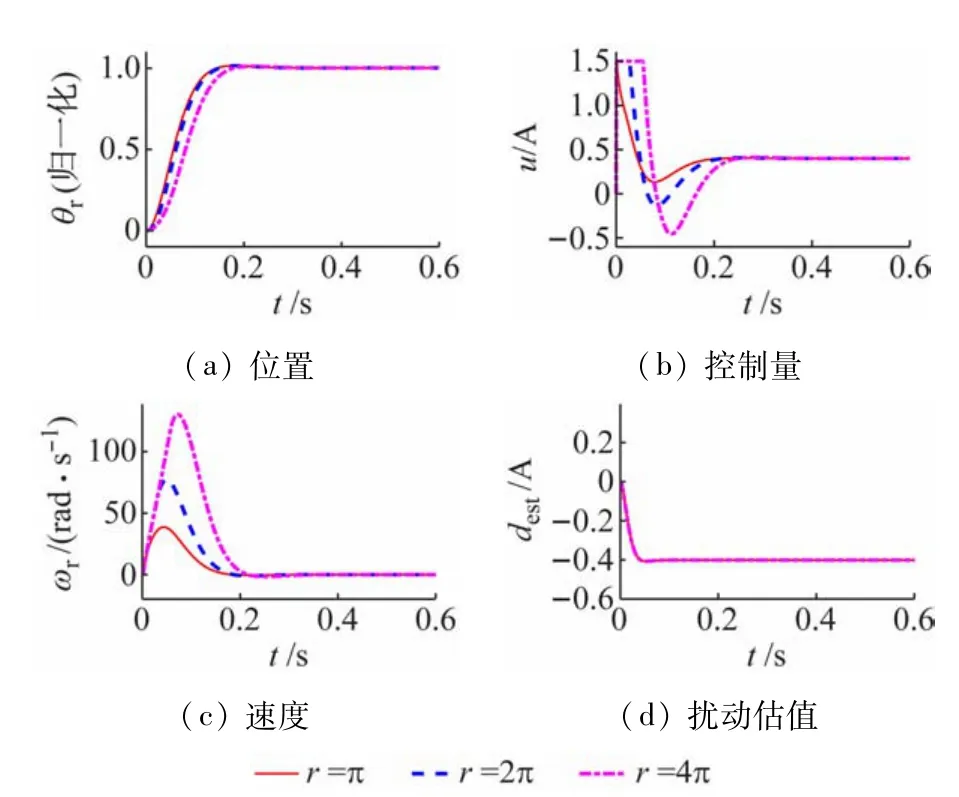
图6 3种目标角度和半载下鲁棒快速伺服控制的仿真结果

图7 目标角度4π和3种负载下鲁棒快速伺服控制的仿真结果

图8 目标角度6π和3种限速下鲁棒快速伺服控制的仿真结果

表1 仿真所用的控制律参数值
4 基于DSC的实验
采用Texas Instruments公司的TMS320F28335DSC作为主控芯片,利用Code Composer Studio软件进行控制算法编程和实验操作,在一台永磁同步电动机(型号为60CB020C)上进行了实验研究,如图9 所示。电动机的额定转速和转矩为3 000 r/min和0.64 N·m,极对数为4;配有2 500 线的双路正交光电编码器,利用一个磁粉制动器来提供负载。电动机的电流内环和脉宽调制的采样频率是20 kHz。位置控制环分别采用设计的两种控制律,其采样周期为Ts=2 ms。

图9 永磁同步电动机实验装置
控制律参数值以表1 为基准,但实验中由于系统特性的差异,需对某些参数进行微调。在给定r=π和50%负载的情况下,把扰动补偿系数调整为fd=0.95(两种控制律相同),保证所需的稳态精度且降低对测量噪声的敏感度。随后,保持参数值不变,分别在不同负载和给定目标的组合下进行实验。图10 和11 是自抗扰控制在目标分别为π 和2π 时的实验结果,虽然图中扰动估计值看起来差异较大,但系统的位置响应却很接近。图12 显示了目标为4π 时在半载和满载条件下的实验结果,系统都能实现准确控制。需说明的是,当目标为4π时,空载情形下的ADRC 实验未能成功;当目标角度更大时,实验也未能做成,除非降低ADRC控制律的带宽参数值。

图10 目标位移π时自抗扰控制的实验结果
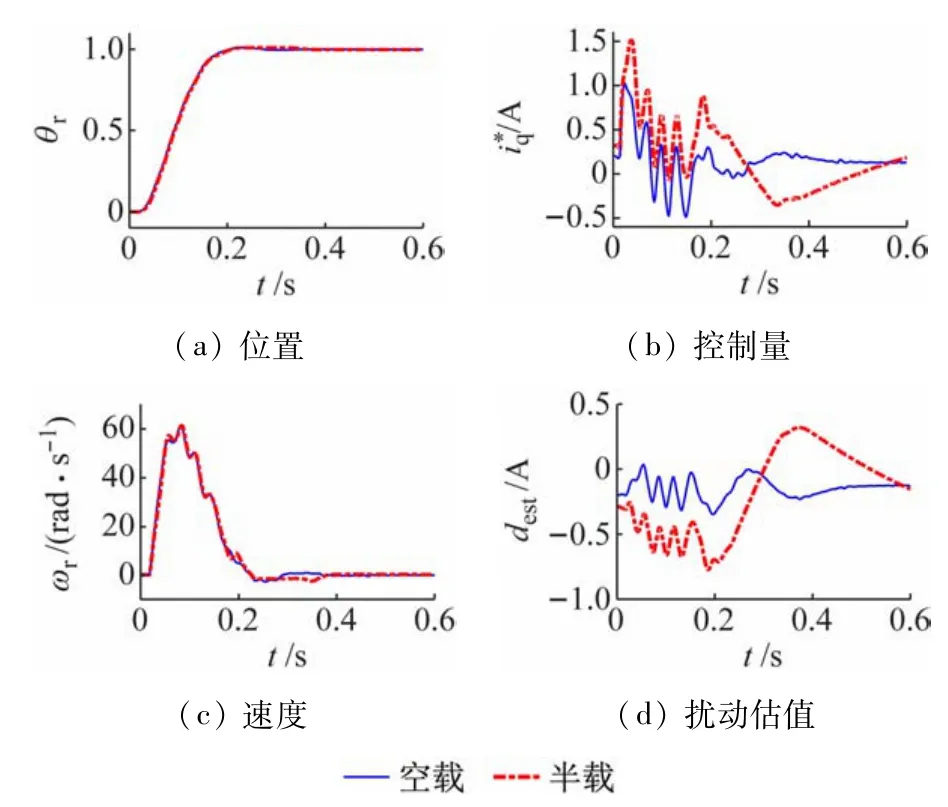
图11 目标位移2π时自抗扰控制的实验结果

图12 目标位移4π时自抗扰控制的实验结果
图13~15 分别是鲁棒快速伺服控制在给定为π、2π和4π 时的实验结果,都实现了准确定位,而且其信号波形比较平滑,说明控制系统运行较为平稳。图16 是鲁棒快速伺服控制在目标为6π、半载时对应3种不同限速值的实验结果。由于限速值的引入,系统能进行大行程的准确位置控制。表2 总结了各种情形下的性能指标,包括超调量(%)和上升时间(即电动机位置首次进入目标的2%邻域的时间)。从表中可以看出,ADRC 在小目标(≤π)的定位性能上具有一定的优势,但鲁棒快速伺服控制在大行程定位具有明显优越性,特别是当目标从π增大到2π乃至4π时,其上升时间反而缩短,这是因为其中的时间最优控制律此时可以发挥主导作用。总体上看,鲁棒快速伺服控制与目前流行的ADRC 相比,有较大的竞争力,值得关注。
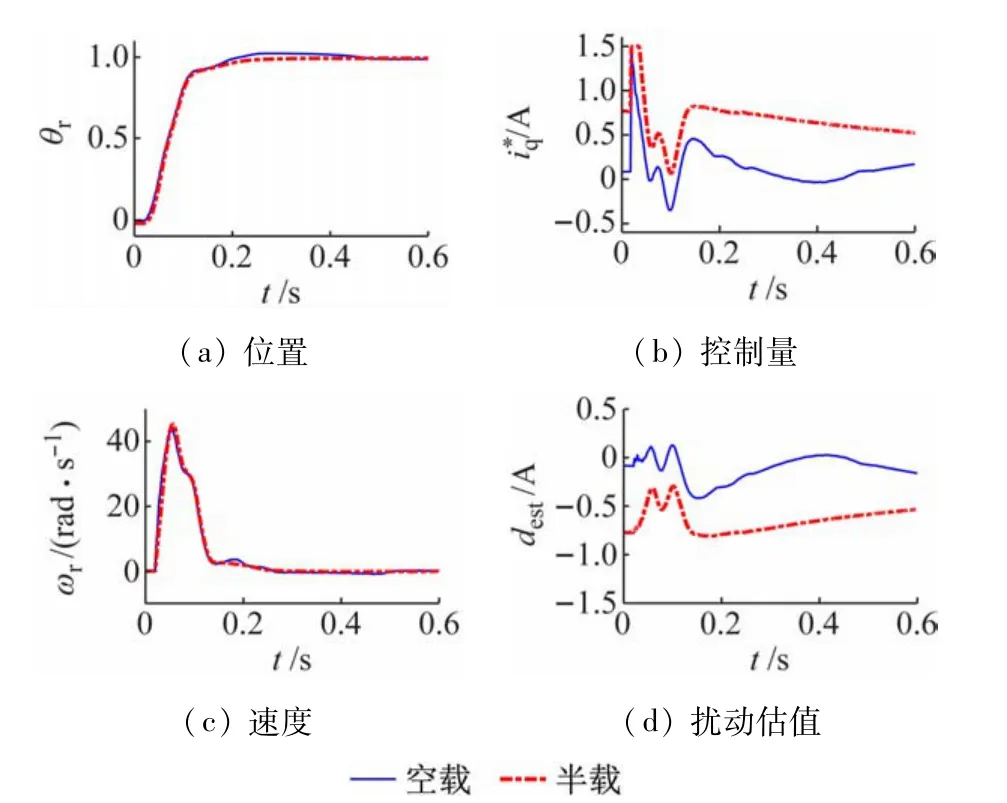
图13 目标位移π时鲁棒快速伺服控制的实验结果
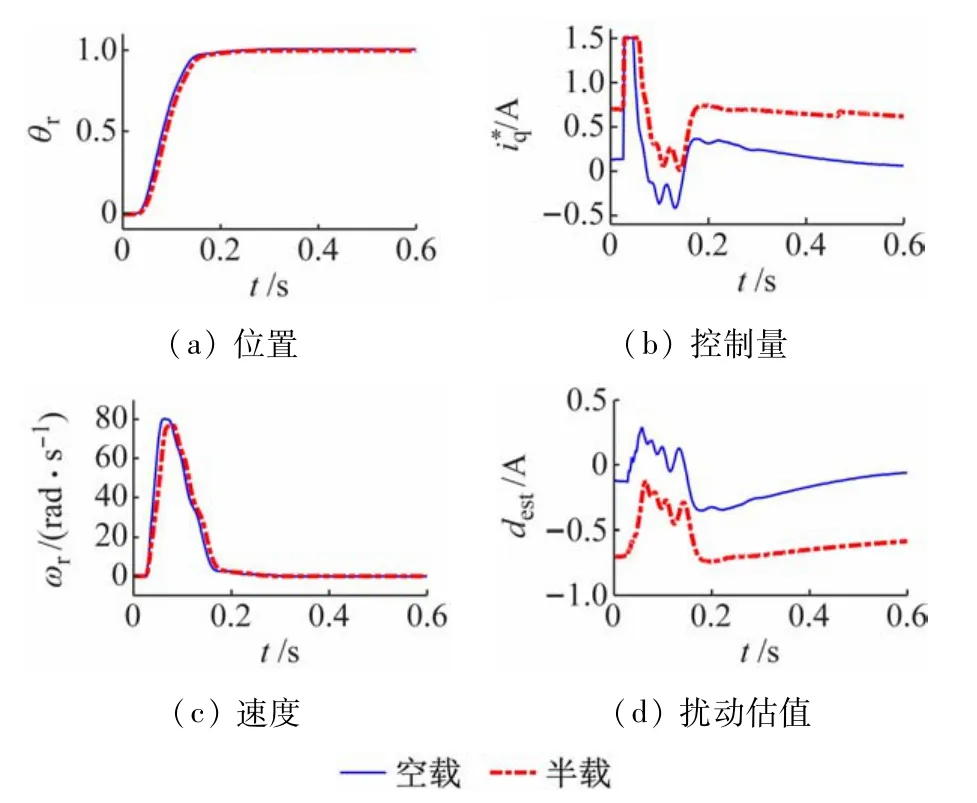
图14 目标位移2π时鲁棒快速伺服控制的实验结果
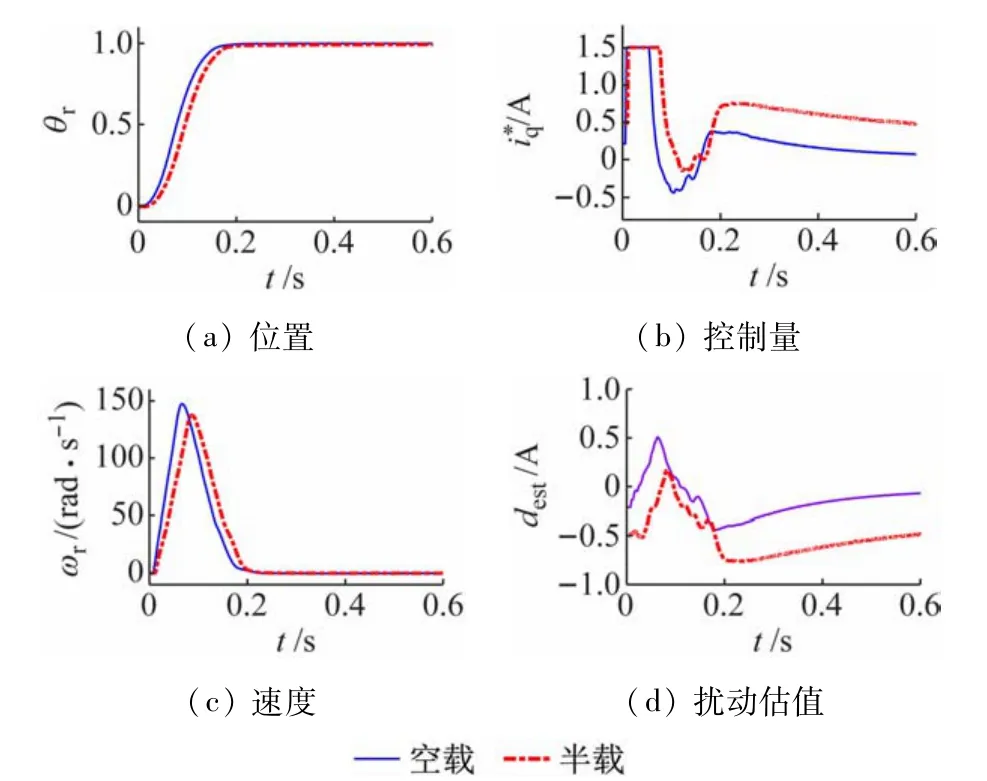
图15 目标位移4π时鲁棒快速伺服控制的实验结果
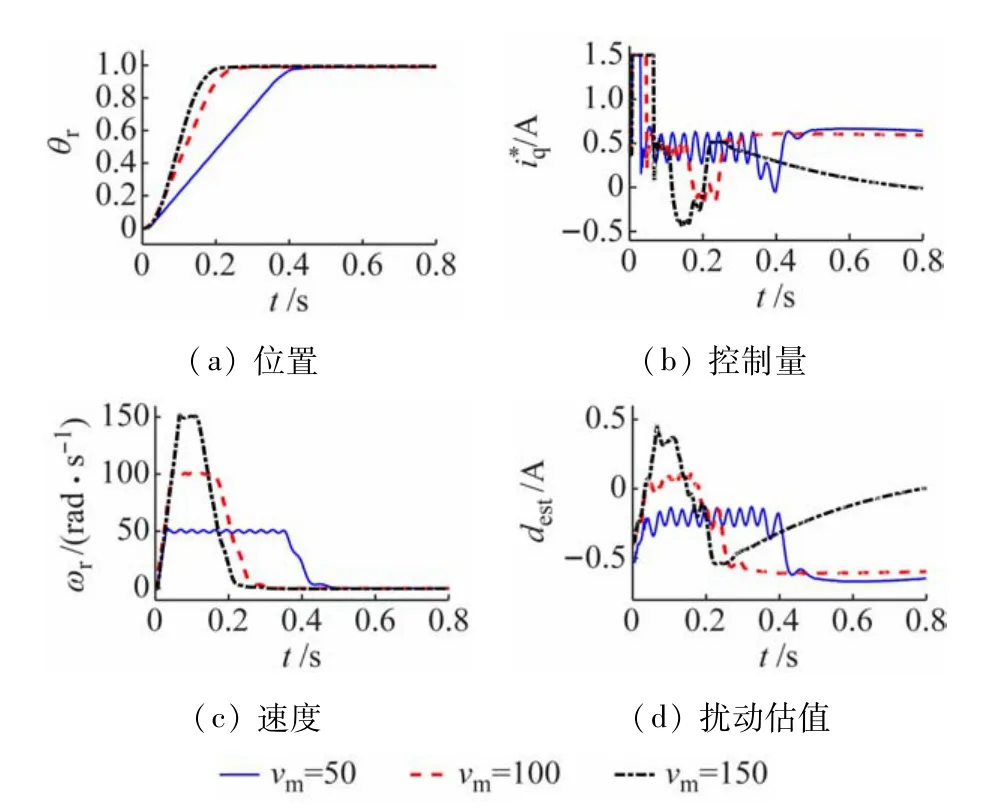
图16 目标位移6π时鲁棒快速伺服控制的实验结果

表2 实验结果比较
5 结语
针对永磁同步电动机伺服系统,在磁场定向模式和电流内环闭环的情况下,以转矩电流作为控制量,电动机转角作为输出量,分别采用自抗扰控制和鲁棒快速伺服控制技术,设计了高性能位置伺服控制律。通过MATLAB仿真和基于TMS320F28335 的实验研究,展示了控制方案的性能差异。学生通过该实验案例,学习了模型简化、控制器参数化设计、实时编程和实验调试方法,领悟到把先进技术应用于工程实践的理念。接下来将引入其他典型的控制手段,丰富该实验的技术内涵,使它成为一套综合实验软件包、可灵活地组态和应用于电动机伺服系统。
