基于改进灰狼优化算法应力强度因子预测模型

潘海珠，葛海淼，苏小红，袁 琪

（1.齐齐哈尔大学计算机与控制工程学院，黑龙江齐齐哈尔 161006；2.哈尔滨工业大学计算机科学与技术学院，哈尔滨150001）

0 引言

由功能梯度材料（Functionally Graded Material，FGM）制备的受力部件在循环应力或应变作用下会产生局部结构变化，形成疲劳裂纹并产生扩展，对构件及工程安全构成严重威胁。裂纹尖端的应力场强度，即应力强度因子（Stress Intensity Factor，SIF），是表征材料断裂的重要参量，它和材料属性、应力大小和裂纹几何尺寸等因素密切相关。由于FGM 属性呈现梯度变化，使得传统的理论解析求解方法较难求解裂纹问题。随着信息技术不断发展，许多学者尝试运用人工智能方法与传统理论求解模型相结合，来解决复杂的断裂问题［1-5］。其中，支持向量回归（Support Vector Regression，SVR）是支持向量机（Support Vector Machine，SVM）在解决回归和预测问题中的扩展［6］，作为一种高效的机器学习方法，采用最小化经验误差和最大化几何边缘策略，常用来解决小样本、非线性问题。但是，SVR 方法在内核参数选择上存在一定困难，易使模型陷入局部最优，文献［7-12］中提出了基于SVR的改进算法进行参数优化，可提高预测模型的准确性和鲁棒性。改进的SVR 预测模型研究可以作为传统断裂力学研究的新手段，用于快速得到力学本构模型和控制方程的函数表达形式。基于概率变异灰狼优化算法的SVR是支持向量回归的一种改进类型，通过变异的灰狼优化算法对SVR 的几个主要参数进行优化，实现小样本情况下的SIFs预测。

本文以含有任意方向裂纹的一般属性FGM 为研究对象，分析应力强度因子与FGM属性、裂纹长度、裂纹角度等的关系，提出了SVR结合概率变异的灰狼优化算法（Probability Mutation Grey Wolf Optimization Algorithm，MP-GWO），通过优化SVR 参数，运用分层指数模型方法获取数据，训练一个以裂纹几何参数及FGM属性等特征值为输入，应力强度因子为输出的预测模型。在传统力学建模方法获取数据基础上，提出一种新的基于机器学习方法的断裂力学预测模型，并通过有效实验验证该模型的适用性和精确性。本文的目的在于运用分层指数模型获取离散应力强度因子，训练一个支持向量回归模型，提出了概率变异灰狼优化（MP-GWO）算法对模型参数进行优化，将这些离散应力强度因子在高维空间拟合成一个超平面，实现了运用机器学习方法拟合出隐式的本构关系，对不同材料参数及裂纹几何参数条件下的SIFs预测；对比传统的灰狼优化算法，提出的改进算法，即基于MP-GWO算法的支持向量回归模型能更好抑制算法陷入局部最优，得到的应力强度因子预测模型泛化能力更优。

1 MP-GWO-SVR原理

1.1 SVR基本原理

设样本集｛（xi，yi），i=1，2，…，n｝，其中，xi∈RD为数据样本的输入值；yi∈R为样本的输出值；D为样本维度。对于非线性的SVR问题，可以引入映射函数φ（·），将输入数据映射到高维特征空间F中，定义回归预测模型

式中：w 为权重向量；b为常数；f（x）为回归预测模型输出。引入松弛变量（，ξi），定义f（xi）与yi的损失函数

式中：C是惩罚因子；ε 是最大允许误差。目标函数为最小化损失函数J，引入拉格朗日乘数及核函数可以将目标函数转化为如下对偶形式：

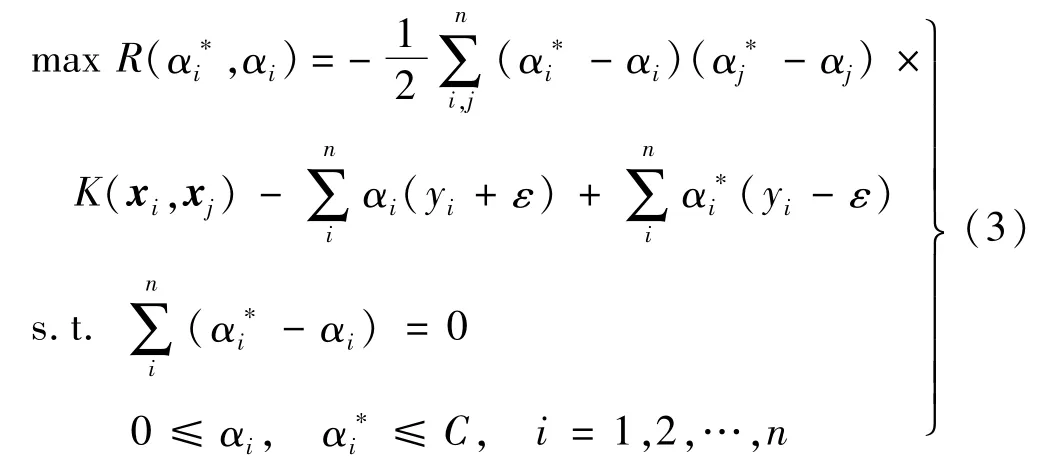
式中：αi和为拉格朗日乘数；K（xi，xj）=φ（xi）φ（xj）为核函数，定义径向基核函数

式中，σ为内核参数［7］。通过求得的αi和，可以得到SVR表达式

式中：xr和xs是任意的支持向量；SVs 为支持向量的数量。

在SVR 应用中，参数惩罚因子C、RBF 核函数参数σ 和最大允许误差ε 对模型的学习能力和泛化能力有重要影响，因此对这些参数进行优化尤为重要，本文提出使用MP-GWO算法优化SVR的3 个参数。

1.2 概率变异灰狼优化（MP-GWO）算法

（1）灰狼优化（Grey Wolf Optimization，GWO）算法。GWO算法［13］是一种模拟狼群狩猎行为的群体智能优化算法。GWO 算法在搜索空间随机产生灰狼种群，将狼群划分为不同等级的α 狼、β 狼和γ 狼，剩余个体为ω狼；通过包围猎物、攻击猎物行为实现对目标猎物的猎杀，获得待优化问题的最优解。

GWO的包围行为首先确定灰狼与猎物之间的距离，更新灰狼的位置，其数学表达式如下：

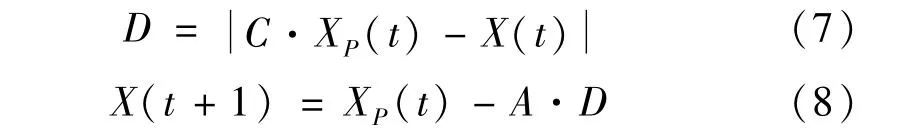
式中：t表示当前的迭代次数；D表示灰狼与猎物的距离；XP（t）为第t代猎物的位置；X（t）为第t代单只灰狼的位置向量；A和C为随机常系数，

r1和r2为［0，1］间的随机数；数值ɑ随迭代次数增加从2 递减至0，表达式为

l为当前迭代次数；nmax为最大迭代次数。

GWO的狩猎行为在α狼、β狼和γ 狼的领导下进行，其数学表达式为：

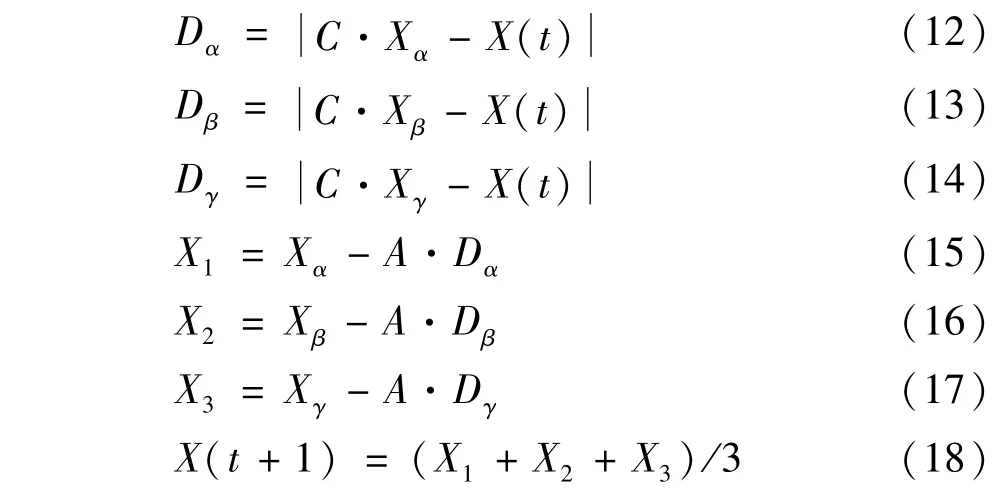
式中：Xα、Xβ、Xγ分别为头狼α 狼、β 狼和γ 狼位置；Dα、Dβ、Dγ分别为狼群剩余个体ω狼与α狼、β 狼和γ狼的距离；X1、X2、X3分别用于计算3 个头狼的运动轨迹；X（t+1）为灰狼更新后的位置。GWO 算法通过迭代过程更新狼群位置，逐渐逼近猎物，完成对猎物的捕食。

GWO算法的全局搜索能力体现在随机数A和C，但该算法在初始化群体时就倾向于搜索可能存在的最优解，这种搜索策略易导致结果局部最优［14-17］。为改进GWO算法的全局搜索能力，并进一步增强算法的鲁棒性，本文提出一种变异策略的灰狼寻优算法。

（2）MP-GWO 算法。MP-GWO 算法在生成狼群位置X（t+1）后，以递减概率对狼群位置进行变异计算。变异计算分为两种，分别为交叉变异和普通变异。狼群中的个体根据变异概率产生某一种变异。

交叉变异根据当前最优解Xα和当前狼的位置X（t+1）决定ω狼的位置，交叉变异具体表达式如下：

式中：r3，r5为［0，1］间的随机数；Mp为变异概率阈值。

普通变异根据当前狼位置X（t+1）和搜索空间范围决定ω狼的位置，普通变异的表达式如下：

式中：r4为［0，1］间的随机数；ub和lb分别为搜索空间上下界。式（19）、（20）限制条件中的随机数r5用于控制交叉变异或普通变异是否发生。

为保证狼群个体只能产生一种变异，变异概率阈值为［0，0.5］之间的值。为保证算法收敛，变异概率阈值应随迭代次数增加而减小，变异概率阈值Mp表达式如下

式中：p为变异概率常数，为［0，0.5］间的值。

MP-GWO算法的具体步骤如下：

（1）初始化GWO算法的参数。狼群中狼的数量Nw，变异概率常数p，搜索空间上下限ub和lb，搜索空间维度D，最大迭代次数nmax。

（2）计算灰狼个体的适应度，根据适应度值的大小进行排序，前3 名灰狼位置设置为Xα，Xβ，Xγ。

（3）根据式（9）～（11）、（21）更新A，C，ɑ，Mp的值。

（4）遍历每个狼个体，根据式（12）～（18）更新狼的当前位置；当r5∈［0，Mp］，其中r5为［0，1］间随机数，根据式（19）计算当前狼位置的交叉变异值，更新位置；当r5∈［MP，2MP］，根据式（20）计算当前狼位置的普通变异值，更新位置。

（5）判断每一个狼个体的位置是否超出搜索空间上下限ub和lb，如位置值大于ub，则将当前狼位置值设为ub；如位置值小于lb，则将当前狼位置值设为lb。

（6）判断是否达到最大迭代次数，若达到则跳出算法，输出最优值Xα；否则，设置l=l+1，跳转到步骤（2）。

2 应力强度因子计算

图1 为含有任意方向裂纹具有一般材料属性功能梯度材料示意图。材料无限长且厚度为l，所含裂纹与材料梯度变化方向的角度为α。如图1 所示，在x′Oy′坐标系下，裂纹两个端点坐标分别为（ɑ，0），（b，0）。由于任意属性FGM的裂纹问题难于解析求解，采用分层指数模型来求解一般材料属性FGM断裂问题，假设FGM实际属性可以用指数函数、线性函数、幂函数等一般连续性函数来描述［18］。充分利用指数型材料的控制偏微分方程易求解这一特点，通过傅里叶变换、微分算子等方法求解应力场和位移场；结合裂纹问题的边界条件和位移条件，求解奇异积分方程组，求得混合型应力强度因子k值如下：

图1 含任意方向裂纹的功能梯度材料示意图

式中：κ、δ 为材料参数；n为分层指数模型划分的层数；f1、f2为求解奇异方程组引入的可求解函数。运用该方法求得的应力强度因子用于训练SVR预测模型。

3 MP-GWO-SVR应力强度因子预测模型

由于SVR的性能主要受惩罚因子C、RBF核函数参数σ和最大允许误差ε影响，使用MP-GWO算法实现对SVR 3 个参数进行优化。生成的SIFs 预测模型计算步骤如下：

（1）样本数据初始化。材料属性变化形式、模量比、裂纹相对长度和裂纹角度为输入值，裂纹尖端应力强度因子为输出值，组成样本集和标签集（Sample_all，label_all）。考虑3 种材料属性变化形式，即材料属性变化分别用指数函数、线性函数和幂函数来描述；材料上下表面弹性模量比取值为（2，2.5，3，4，5）；裂纹相对长度的取值为（0.1，0.15，0.2，0.25，0.3，0.35，0.4，0.45，0.5）；裂纹角度的取值为（0π，0.05π，0.1π，0.15π，0.2π，0.25π，0.3π，0.35π，0.4π，0.45π，0.5π）；样本总数为202 个；随机选择1/2 样本作为训练样本（Sample_train），共101 个样本，其标签为label_train，其他样本作为测试样本（Sample_test），共101 个样本。

（2）参数初始化。初始化狼群数量Nw=10，其中头狼α、β和γ占狼群数量为3，剩余个体ω 狼占狼群数量为7；变异概率常数p=0.5；搜索空间上下限ub=［100，100，0.2］和lb=［0.01，0.01，0.001］；搜索空间维度D=3；nmax=10。

（3）使用Sample_train 训练SVR，使用MP-GWO算法寻找SVR的最佳参数C、σ和ε。

（4）使用C、σ 和ε 实现SVR 的建模，得到SVR模型model_SVR。

（5）使用model_SVR预测Sample_test的值，得到测试样本的预测值label_test_SVR。

4 实验结果及分析

以幂函数表征材料属性变化形式，材料上下表面弹性模量比值为2.5 的特征数据为例，将SVR模型预测结果，即无量纲化应力强度因子kI（ɑ）、kI（b）、kII（ɑ）和kII（b）分别标注为Label1、Label2、Label3和Label4，图2～5 分别给出不同裂纹参数下MP-GWOSVR模型与GWO-SVR模型的SIFs预测值，以及运用分层法求解SIFs（真实值）的变化曲线。

图2 基于GWO-SVR的SIFs预测模型预测结果

对比图2（a）和图4（a）可以看到，对于不同长度的裂纹，当裂纹角度较大时（如0.4π，0.45π，0.5π），应力强度因子kI（ɑ）较真实值有较大的差别。比较图3（a）和图4（a），可以看到MP-GWO-SVR 模型预测SIFs曲线较分层模型求解SIFs 曲线变化趋势相似度都很高；尤其注意到当裂纹角度较大时（如0.4π，0.45π，0.5π），两种模型给出曲线的变化趋势几乎一致。这种现象说明MP-GWO-SVR 模型较GWO-SVR模型在Label1上有更好的拟合度。对比图2（b）、图3（b）和图4（b），可以看到MP-GWO-SVR 模型得到了与分层模型求解SIFs曲线相似度很高的拟合曲线，而GWO-SVR模型对于裂纹角度较大时预测结果与真实值偏离较大，这种现象说明MP-GWO-SVR 模型在Label2上可得到较为理想的拟合结果。对比图2（c）、图3（c）和图4（c），可以看到情况有所不同。在裂纹相对长度为0.1 和0.2 时，GWO-SVR 和MP-GWOSVR两种模型预测SIFs曲线都有变形，但是从图中可以看到，MP-GWO-SVR模型的预测曲线变形程度明显小于GWO-SVR 模型；当裂纹相对长度为0.3 时，GWO-SVR模型和MP-GWO-SVR 模型给出的SIFs 预测曲线拟合度较高；当裂纹相对长度为0.4 和0.5 时，GWO-SVR模型的SIFs预测值随裂纹角度变化出现明显波动，相比真实值曲线有明显的变形，而MP-GWOSVR模型的SIFs预测曲线与分层模型求解SIFs 曲线形状基本一致。这种情况说明对Label3，GWO-SVR和MP-GWO-SVR模型对SIFs 拟合结果都有的误差，但MP-GWO-SVR模型的预测误差相对较小。对比图2（d）、图3（d）和图4（d），可以看到GWO-SVR 模型给出的SIFs拟合曲线较分层模型求解SIFs 曲线有较明显的变形，而MP-GWO-SVR模型给出的拟合曲线较分层模型求解SIFs曲线拟合度很高，说明MP-GWO-SVR模型在Label4上拟合能力优于GWO-SVR模型。以上分析结果与图5 中的SIFs样本点对比结果一致。

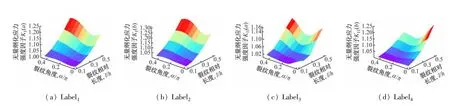
图3 基于MP-GWO-SVR的SIFs预测模型预测结果

图4 分层模型求解SIFs

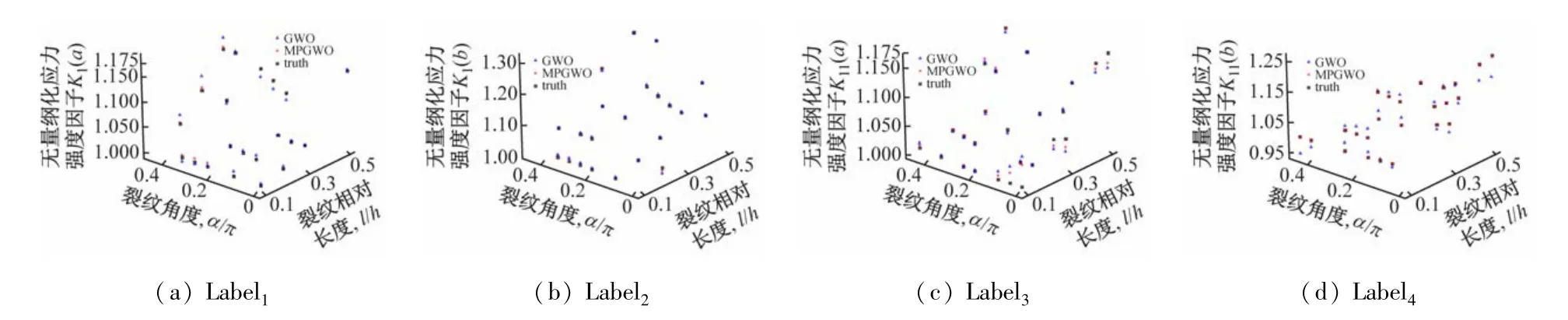
图5 GWO-SVR、MP-GWO-SVR预测值与真实值作对比

为了进一步比较MP-GWO算法和GWO算法的性能，本文采用均方误差（Mean Square Error，MSE）和误差范围百分比（Percentage of Error Range，PER）两种度量标准分别对基于两种算法的SVR 生成SIFs 预测模型进行预测精度评价，其定义如下：

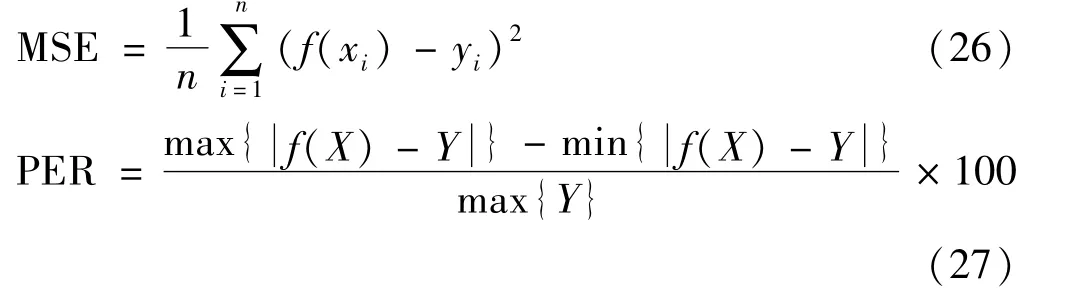
式中：n为样本数；f（xi）为样本的预测值；yi为样本的真实值（即运用分层模型得到的解）；f（X）为预测值向量；Y为真实值向量；max｛·｝为求目标集合的最大值；min｛·｝为求目标集合的最小值。

选取其中两组数据为例，分别计算其均方误差及误差范围百分比，结果如表1、2 所示。由表1 可见，基于算法GWO 的SVR 模型在Label1、Label2、Label3和Label4上的均方误差在4.583 5 ×10-4～3.939 1 ×10-5之间，其中Label1和Label2的均方误差较小，Label3和Label4的均方误差较大；基于算法MP-GWO的SVR模型在各标签上的均方误差范围为7.556 2 ×10-5～5.364 4 ×10-6，其中Label1的均方误差较小，Label2、Label3和Label4的均方误差较大。对比算法GWO和MP-GWO，可以看到MP-GWO-SVR 模型的均方误差在各个Label 上都小于GWO-SVR 模型。这种现象说明MP-GWO 算法构建的预测模型有较高的泛化能力。从表2 可以看到，基于算法MP-GWO的SVR模型在Label1、Label2和Label3上的误差范围都小于GWO-SVR模型，两者在Label4上有相似的误差范围。这种现象表明，MP-GWO 算法较GWO 算法相比，其SVR模型不易出现偏离实际值过大的预测值，有更好的稳定性。

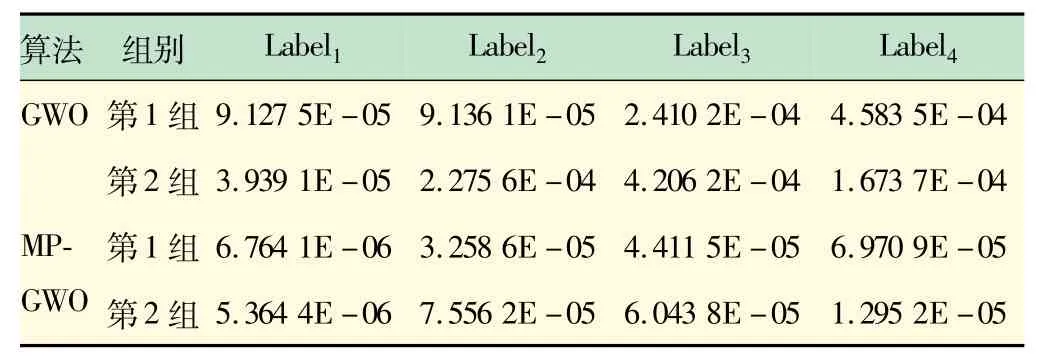
表1 两种算法构建预测模型的均方误差对比

表2 两种算法构建预测模型的误差范围对比 %

5 结语

本文以含任意方向裂纹的功能梯度材料断裂问题为研究对象，运用机器学习方法，用小样本数据训练一个支持向量回归模型，实现对含有任意方向裂纹的一般属性功能梯度材料应力强度因子的预测分析。本文在传统的基于灰狼优化算法的SVR 模型基础上提出了一种改进算法，即概率变异灰狼优化算法，构建SVR模型预测SIFs。该算法优化SVR参数，获取模型的预测精度比基于传统灰狼优化算法支持的预测模型有显著提高，从得到的误差范围来看，概率变异灰狼优化算法SVR预测模型的预测结果与样本数据的拟合度更好。本文在传统断裂力学研究方法基础上运用智能优化算法，为断裂力学问题研究提供了一种可扩展的研究模式，该方法将在今后的断裂力学理论与实验研究中将发挥重大作用。

·名人名言·

对真理的追求要比对真理的占有更可贵。

——爱因斯坦