基于RT-PPP 的低轨卫星实时高精度时间同步方法

王伟，臧文驰，彭竞，龚航，孙广富

( 国防科技大学 电子科学学院，长沙 410073 )

0 引 言

低轨卫星由于特殊的应用和科研的需要得到迅速的发展，在很多方面发挥了重大的作用. 低轨卫星距离地面仅1 000 km 左右，相比GNSS 系统具有落地功率高，抗干扰能力强的优势，且低轨卫星的几何构型变化快，可以加快精密定位的收敛时间[1-2]. 因此，通过低轨卫星提供导航增强服务的方式得到了广泛关注，对低轨导航增强的研究也越来越多.

低轨导航增强系统的目标之一是实现地面用户的高精度定位和快速收敛，要实现这一目标就要实现低轨导航增强卫星的亚米级的定位精度和纳秒级的时间同步精度[3]. 对于庞大的低轨星座而言，实现低轨星座的整网时间同步是赋予低轨卫星系统导航能力的必要条件. 然而，面对数目众多的低轨卫星，通过地面站上注星历的方式对低轨卫星时间同步需要众多的全球地面站，对地面的压力过大[4]. 而星载全球定位系统(GNSS)接收机通过伪距定位授时的方式实现的时间同步精度往往在几十纳秒，无法满足当前低轨导航增强对高精度时间同步的需求[5]. 因此，本文对低轨卫星采用实时精密单点定位(RT-PPP)实现高精度时间同步的可行性展开了研究，利用精密星历和低轨卫星GPS 观测数据对低轨卫星进行钟差解算，实现低轨卫星高精度时间同步，并通过气象、电离层与气候星座观测系统(COSMIC)卫星的实测数据进行验证.

1 低轨卫星RT-PPP 时间同步方法

1.1 星载GPS 观测数据模型

低轨卫星轨道高度一般在200～2 000 km，而电离层集中在60～2 000 km 的大气层区域[6-7]，因此低轨卫星一般位于电离层中，只受轨道高度以上部分的电离层延迟的影响，固体潮、海潮等对其的影响可以忽略不计，并且，低轨卫星轨道高度高于对流层高度，几乎没有对流层的影响[8]. 因此，伪距和载波相位数据的观测模型为：

文中采用GPS 双频Z′信号进行低轨卫星精密单点定位(PPP)钟差解算，选择L1 和L2 频点，对应频率为f1=1 575.42 MHz和f2=1 227.60 MHz . 传统精密单点定位(PPP)方法是对地面接收机，利用全球若干国际GNSS 服务(IGS)跟踪站数据计算出精密卫星轨道参数和卫星钟差，再利用所求得的卫星轨道参数和卫星钟差，对单台接收机采集的相位和伪距观测值进行处理[9]. 由于IGS 事后精密星历存在一定的延迟，并不能获得实时结果，而IGS 的预报产品钟差的预报误差会随着时间的延长不断增大，从而限制了RT-PPP 精度的提高. 自2007 年起，IGS 启动IGS 实时实验项目(IGS-RTPP)[10-12]. 对全球实时跟踪网络的观测数据进行采集并传至各分析中心，再由各分析中心实时估计精密卫星轨道和钟差，并采用基于互联网进行RTCM 网络传输(NTRIP)协议的Internet 方式向全球播发，IGS-RTPP 采用状态空间(SSR)信息格式进行实时卫星轨道和钟差改正信息的发布，SSR 信息是可以对GNSS 的各项误差源进行描述的一种空间表示方法，适合单点定位的误差改正. 多个IGS 分析中心免费播发包含SSR 信息格式的NTRIP 数据流. IGS-RTPP 通过NTRIP 协议播发各分析中心生成的实时卫星轨道和钟差改正数据，用户通过网络访问该列表，选择合适的挂载点，可在较短时间延迟内获得改正数据[13-15]. 基于IGS 的实时产品，本文提出了低轨卫星高精度时间同步方法.

1.2 PPP 的误差改正

本文提出采用信息挂载点为CLK93 的IGS 实时数据流SSR 改正信息进行实时PPP 解算. 由于该数据流为实时估计，因此低轨卫星可以通过星地和星间链路传输在较短的时间内获得精密星历，实时性较高[16]. 此外，解算过程中需将电离层延迟、相对论效应、天线相位中心偏差的影响消除.

1) 电离层延迟

由于电离层延迟与频率的平方成反比, 可以通过无电离层线性组合消除电离层的一阶影响，剩余高阶项偏差可忽略[17]. 在构造无电离层组合时，会放大组合误差，无电离层组合误差方差表达式如下所示：

本文采用GPS 的L1、L2 双频无电离层组合，经式(4)计算，误差放大系数约为2.98.

2) 天线相位中心偏差(PCO)和天线相位中心变化(PCV)

对GPS 观测值进行天线改正时，必须同时考虑PCO 和PCV. PCO 指天线物理中心与电相位中心之间的偏差，该偏差与高度角和方位角有关，PCV 是瞬时天线相位中心与平均相位中心间的差异，两者在改正时可以通过IGS 提供的后缀为atx 的文件修正该偏差，修正后该偏差可忽略[18].

3) 相对论效应偏差

通过模型可对相对论效应偏差进行消除，经过模型改正后该偏差在毫米量级[19]，可忽略.

1.3 处理流程

低轨卫星搭载星载GPS 接收机，直接观测得到GPS 双频伪距和载波相位观测值，实时精密星历可以通过地面上注给低轨卫星，并通过星间链路将精密星历等辅助信息播发给整个星座，从而实现PPP 钟差解算. 数据获取原理示意图及实时PPP 解算流程图如图1～2 所示.

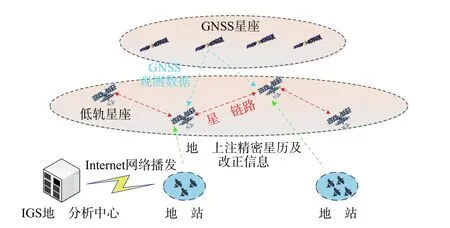
图1 低轨卫星数据获取原理示意图

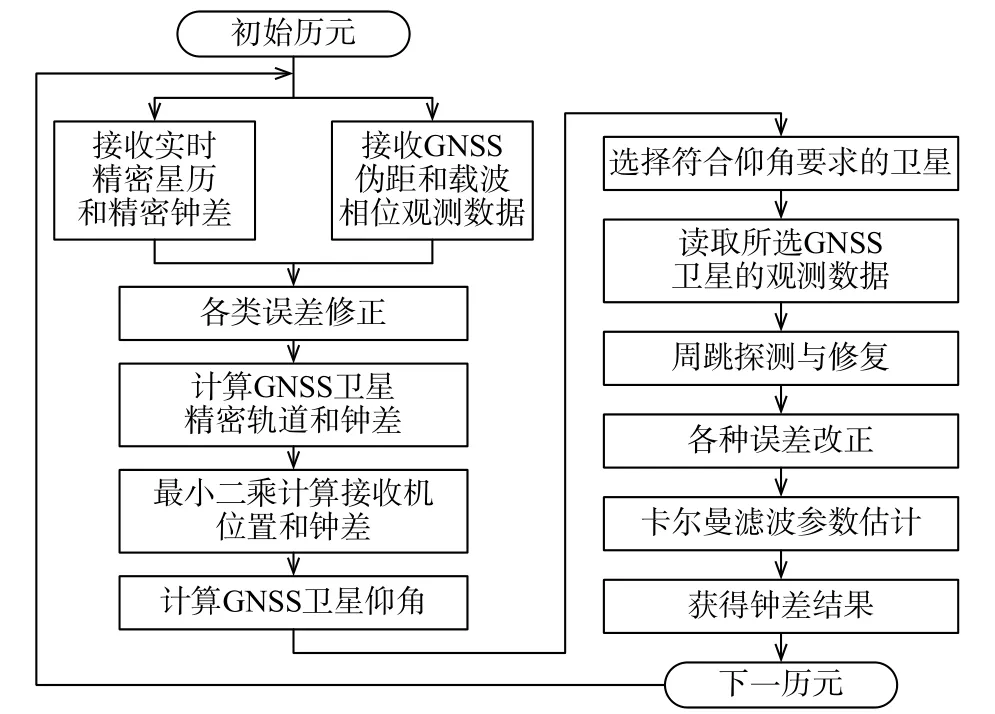
图2 低轨卫星实时PPP 解算流程图

2 实验分析

本文利用COSMIC 卫星的实测数据，分别采用广播星历伪距的方法、IGS 实时数据流SSR 改正信息的RT-PPP 时间同步方法和IGS 事后精密星历的PPP 时间同步方法，对COSMIC 卫星进行数据处理和时间同步结果进行分析，并对3 种方法的结果进行比较.

COSMIC 是台湾太空中心 (NSPO)和美国大学大气研究联盟(UCAR)合作的用以建立全球大气即时观测的卫星任务. COSMIC 是一个由6 颗卫星构成的星座，分布于6 个轨道面，轨道倾角为72°，近圆形轨道，轨道间赤经夹角为24°，轨道高度为700～800 km，每颗卫星重约62 kg[20-21]. COSMIC 卫星上安装有GPS 星载双频接收机，可以接收GPS 双频数据，并且在COSMIC 官方网站上提供了COSMIC 卫星的数据间隔为1 s 的伪距载波相位观测数据，可以供用户进行处理，还提供了COSMIC 卫星的采样率为1 min 的精密轨道数据和采样率为30 s 的精密钟差数据，为用户提供参考[22-24]. 但很多历元观测到的GPS 卫星数量少于4 颗，且提供的数据并不连续. 因此本文选择COSMIC 6 号卫星于2019-01-01 T 16:55:00—20:37:00 这一段连续的观测数据进行处理. 为比较不同卫星之间的时间同步结果差异，本文也选择1 号卫星大概于同一时间段的连续观测数据进行处理，但由于2 颗卫星连续可用的观测数据略有不同，因此2 颗卫星的仿真时长稍有差异.

以COSMIC 网站提供的精密轨道和精密钟差作为参考，将3 种不同方法处理观测数据后得到的轨道和钟差进行分析. 处理方案如表1 所示.

表1 COSMIC 卫星观测数据处理方案

表2 给出了6 号卫星和1 号卫星采用方案1 解算得到的轨道和钟差结果与参考轨道和钟差结果的差异统计；表3 给出了采用方案2 和方案3 解算得到的6 号卫星轨道和钟差结果与参考轨道和钟差结果的差异统计；图3 和图4 分别给出了6 号卫星和1 号卫星的轨道钟差结果与参考结果之间的差异，图5 和图6 分别给出了6 号卫星采用3 种方案的钟差结果与参考结果之间的差异比较.

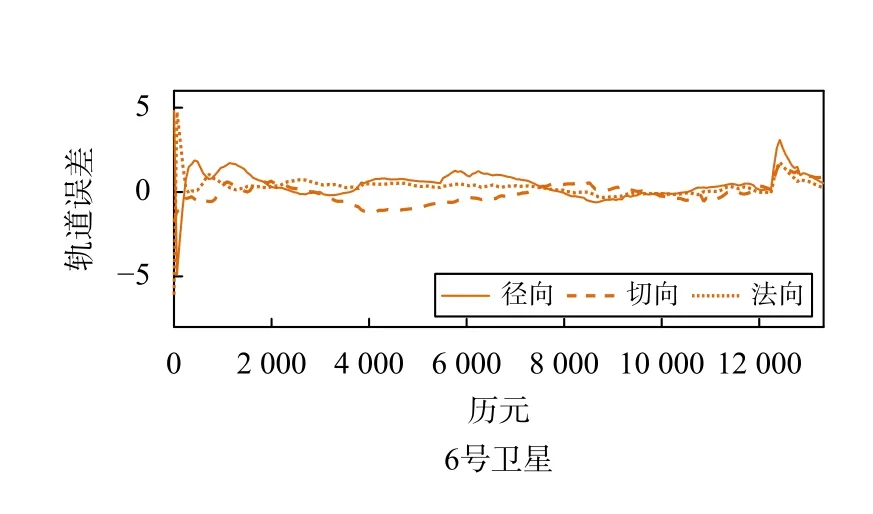
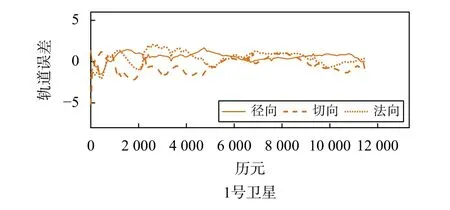
图3 6 号卫星和1 号卫星采用方案1 的轨道解算结果与参考结果的差异

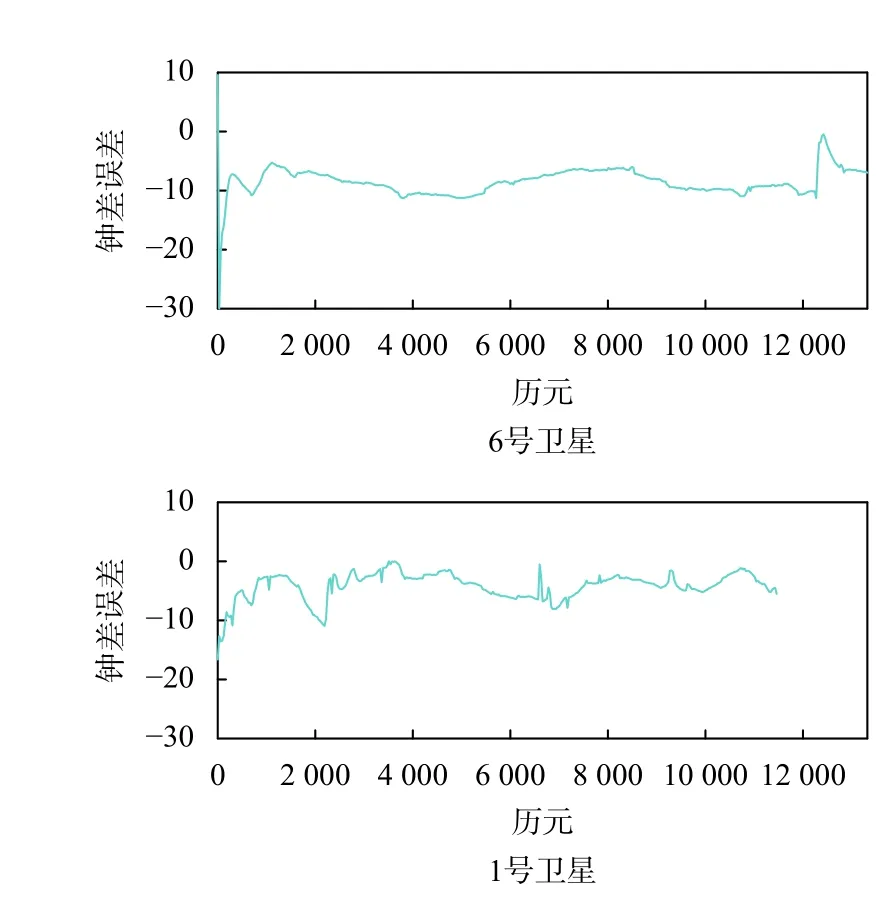
图4 6 号卫星和1 号卫星采用方案1 的钟差解算结果与参考结果的差异

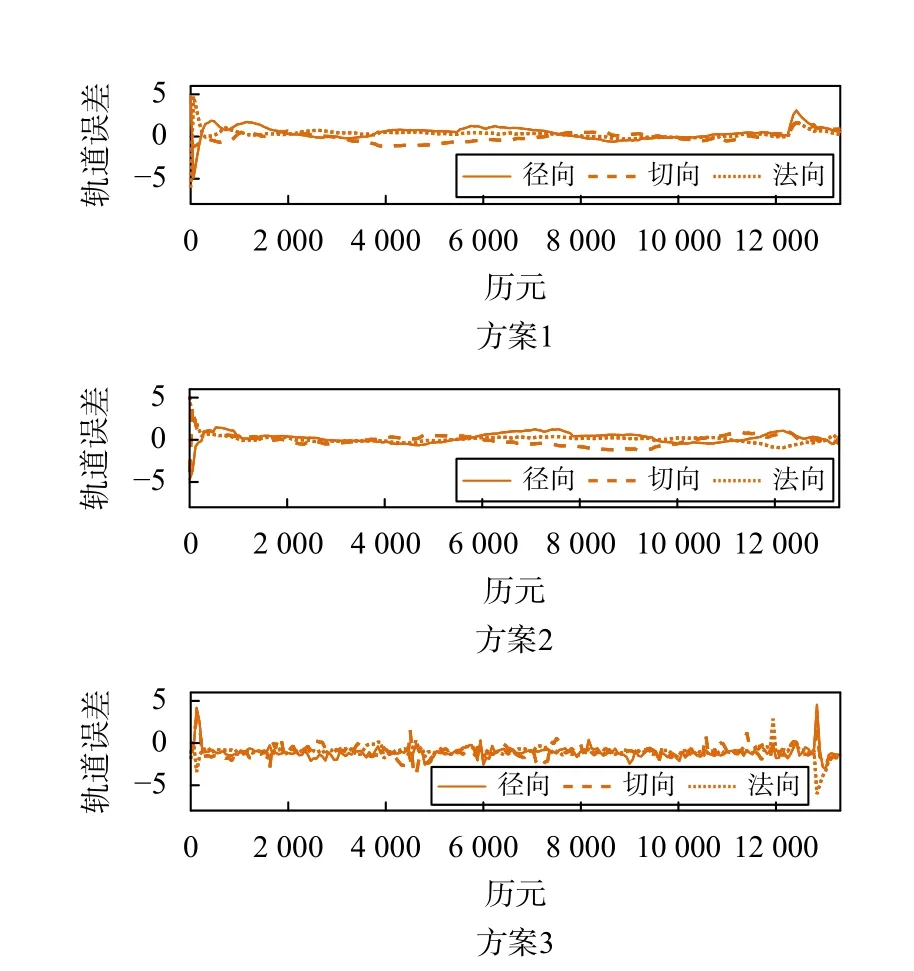
图5 6 号卫星采用方案1、2、3 的轨道解算结果与参考结果的差异

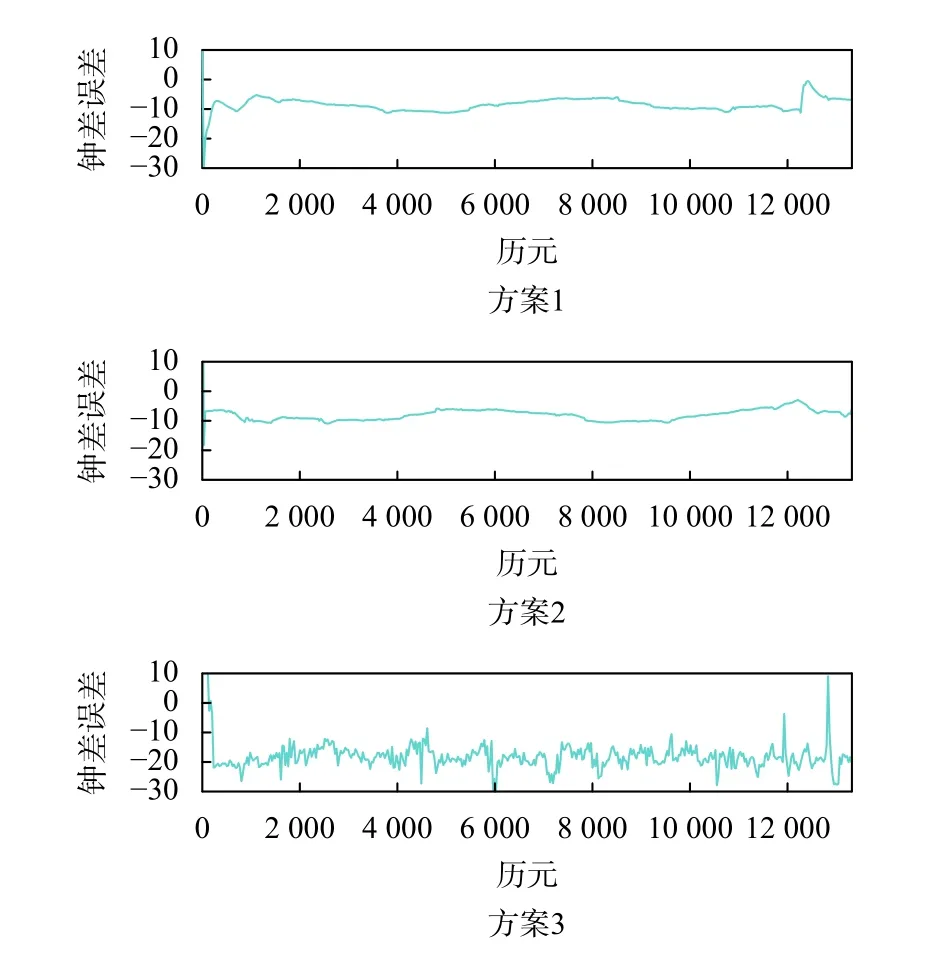
图6 6 号卫星采用方案1、2、3 的钟差解算结果与参考结果差异

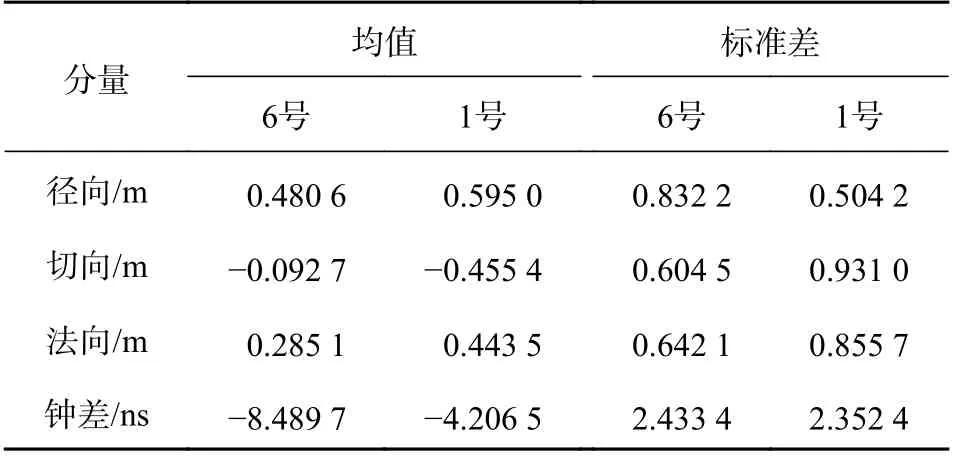
表2 6 号卫星和1 号卫星采用方案1 的解算结果与参考结果的差异统计

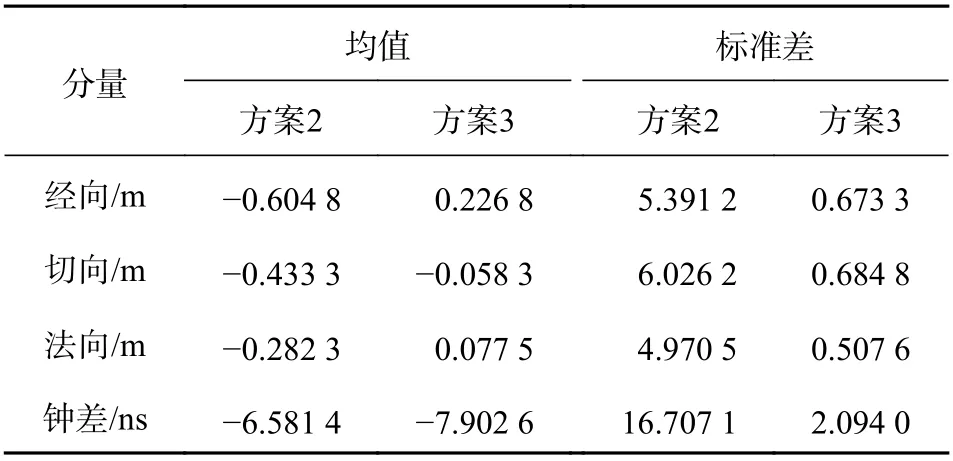
表3 6 号卫星采用方案2 和方案3 的解算结果与参考结果的差异统计

将采用不同的方法对COSMIC 6 号卫星解算得到的结果进行比较，可以看出，采用不同的解算方法得到的结果之间有差异：1) 比较采用广播星历伪距的方法与采用SSR 改正信息实时PPP 的方法，可以看出采用广播星历伪距方法的轨道解算误差在米级，钟差误差在16 ns 左右，而采用SSR 改正信息实时PPP方法的轨道误差在分米级，钟差误差在2.4 ns 左右，相比前一种方法轨道和钟差解算精度提高了一个数量级；2) 比较采用SSR 改正信息实时PPP 的方法与采用事后精密星历PPP 的方法，可以看出采用两种方法的轨道误差都在分米级，钟差误差都在2 ns左右，采用事后精密星历的方法略优于采用SSR 改正信息的方法，但两者结果相差不大.

将采用SSR 改正信息PPP 的方法对COSMIC 6 号卫星和1 号卫星进行GPS 双频观测值的解算结果进行比较，比较结果可以看出两者PPP 的收敛时间为5 min 左右，2 颗卫星得到的轨道误差的标准差在分米级，钟差误差分别在2.4 ns 和2.3 ns 左右，两者标准差相当，但6 号卫星和1 号卫星的解算钟差均值分别为−8.489 7 ns 和−4.206 5 ns，两者相比仍然有4.3 ns 左右的均值差异，原因可能是由于在解算过程中没有扣除接收机通道时延，导致不同卫星解算的钟差误差存在偏差.

为验证6 号卫星与1 号卫星之间的均值偏差，采用方案2 和方案3 对COSMIC 1 号卫星进行了解算.表4 给出了采用方案2 和方案3 解算得到的1 号卫星轨道和钟差结果与参考轨道和钟差结果的差异统计；图7 和图8 分别给出了6 号卫星和1 号卫星采用方案2 和方案3 的钟差解算结果与参考结果之间的差异.

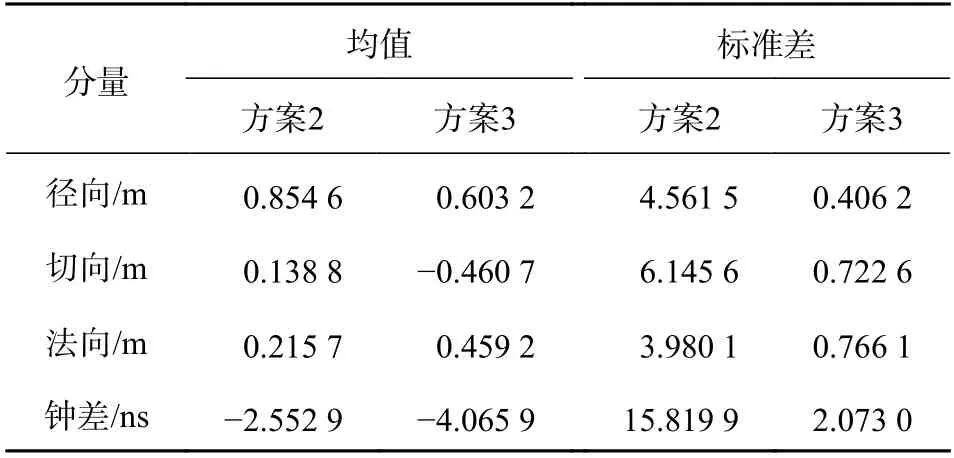
表4 1 号卫星采用方案2 和方案3 的解算结果与参考结果的差异统计

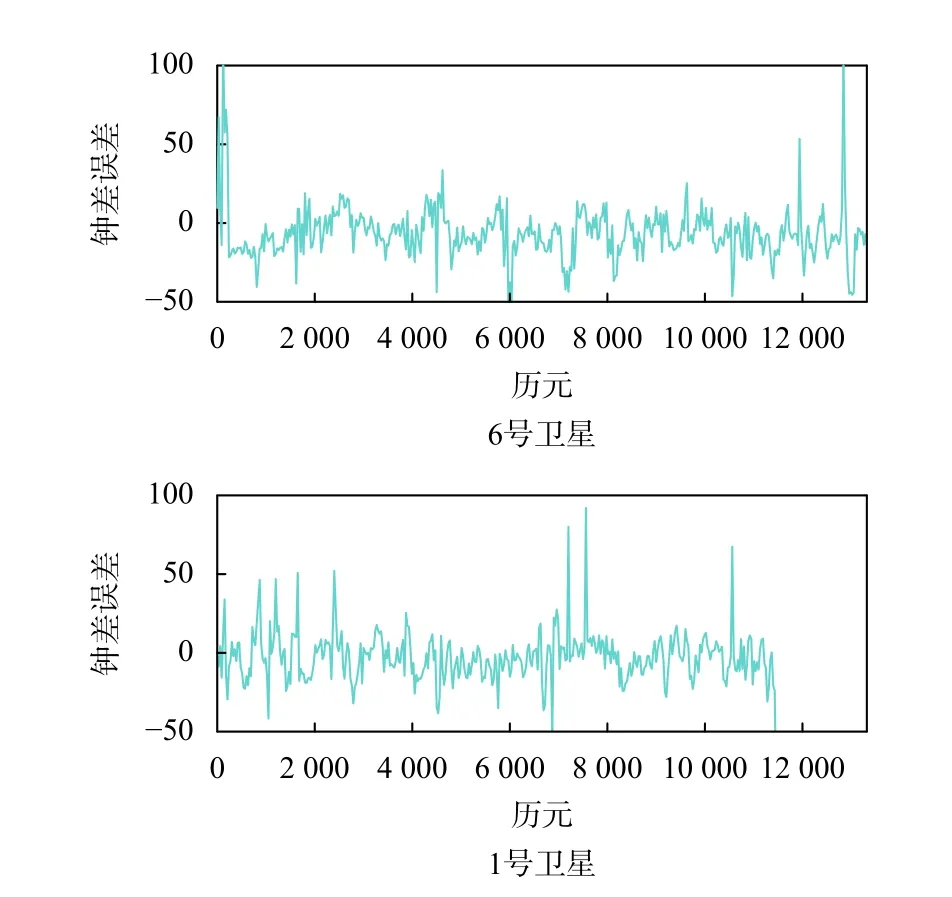
图7 6 号卫星和1 号卫星采用方案2 的钟差解算结果与参考结果的差异

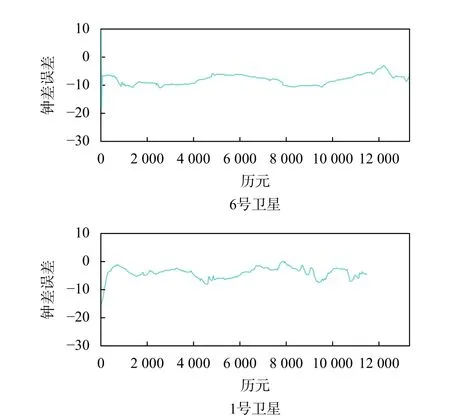
图8 6 号卫星和1 号卫星采用方案3 的钟差解算结果与参考结果的差异

对1 号卫星采用方案2 和方案3 进行处理分析，解算得到的轨道和钟差精度与6 号卫星基本一致.6 号卫星与1 号卫星采用方案2 解算的钟差均值约有4 ns 的差异，采用方案3 解算的钟差均值约有3.8 ns的差异，与二者采用方案1 解算的钟差均值差异基本一致，均值都有4 ns 左右的偏差. 因此可能是由于在解算过程中没有扣除接收机通道时延，导致不同卫星解算的钟差误差存在差异.

3 结束语

本文提出对低轨卫星采用PPP 的方式，通过SSR改正信息实时数据流和低轨卫星GPS 双频观测数据进行低轨卫星钟差解算，实现低轨卫星高精度时间同步，并将该方法与采用广播星历伪距的方法和采用事后精密星历PPP 的方法分别进行比较，以及将该方法应用于2 颗不同的COSMIC 卫星进行结果比较.结果表明：采用SSR 改正信息的实时PPP 方法比采用广播星历伪距解算的方法解算精度有较为明显的提升，解算的轨道精度能达到分米级，钟差精度能达到2 ns 左右；采用SSR 改正信息的实时PPP 方法与采用事后精密星历PPP 的方法相比解算精度相差不大，而采用SSR 改正信息的实时PPP 方法可以较好地解决精密星历实时获取的问题，因此该方法为低轨卫星实现实时高精度的时间同步提供了有效参考.

将SSR 改正信息实时PPP 的方法对2 颗不同的COSMIC 卫星进行GPS 双频观测值的解算，得到的2 颗卫星的轨道误差的标准差在分米级，部分历元的解算结果与COSMIC 官方网站提供的精密轨道产品定轨精度仍有1～2 m 的误差，这是由于在解算过程中，未知参数包括每个历元的卫星坐标和卫星钟差以及整周模糊度，因此每个历元至少观测到5 颗卫星，才可以解算未知参数，但在COSMIC 提供的观测数据中，只有不超过7 颗卫星的观测数据，因此解算精度并不不能达到更高的厘米级. 6 号卫星和1 号卫星的解算钟差误差标准差分别在2.4 ns 和2.3 ns 左右，两者标准差相当，但6 号卫星和1 号卫星的解算钟差均值分别为−8.489 7 ns 和−4.206 5 ns，两者相比仍然有4.3 ns 左右的均值差异. 这表明该方法的时间同步仍然会带来卫星间的几个纳秒的误差. 由于在解算过程中没有扣除卫星的接收机通道时延，因此本文认为出现不同卫星解算钟差的均值偏差的原因是由于不同卫星的接收机通道时延引起的，这对具有上百颗卫星的低轨星座而言会产生整个系统几纳秒甚至几十纳秒的时间同步精度，从而影响低轨导航增强卫系统的性能.