校园物联网流量特性分析与建模

李 巧，谭献海

（西南交通大学 信息科学与技术学院，四川 成都 610031）

0 引 言

网络流量体现了网络的行为特征，掌握流量特性对于网络规划设计、性能优化等工作具有指导意义。随着物联网通信的迅猛发展，传输的数据种类日益增多，大量M2M终端产生的流量数据势必会给网络带来强烈冲击和影响[1]。物联网采用M2M通信方式，与传统互联网通信方式差别巨大。物联网中承载的数据流量越来越大，其流量特性与传统互联网流量不同。

文献[2]研究发现，物联网业务不同于传统互联网模式，具有上行占优、终端数量巨大、仅终端发起、时延控制、会话时间较短、终端移动性低等特点。文献[3]对智能电网中无线传感器网络流量在不同算法、不同采样频率和不同时域下进行分析，发现其具有自相似和长相关特性。文献[4]通过对骨干网的研究，发现流量在小时间尺度上表现出非长相关性。

不同物联网场景的网络流量特性不同，针对校园物联网流量的自相似特性和重尾特性研究较少。本文从粗粒度和细粒度两个方面对校园物联网流量进行全面分析，并在此基础上进行仿真验证，对比实验结果和评价指标，确定校园物联网流量报文到达时间间隔的数学模型。

1 流量数据及预处理

实验所用的校园物联网流量来源于新南威尔士大学（UNSW）采集的数据[5]，采集时间为30天，共6 000万条数据，包含了28种不同物联网设备以及3种非物联网设备。结合3GPP组织总结的七大类M2M应用实例[2]，设备可按照类型分为摄像头、开关和控制器、医疗设备、电子设备、手机和电脑五大类，见表1所列。

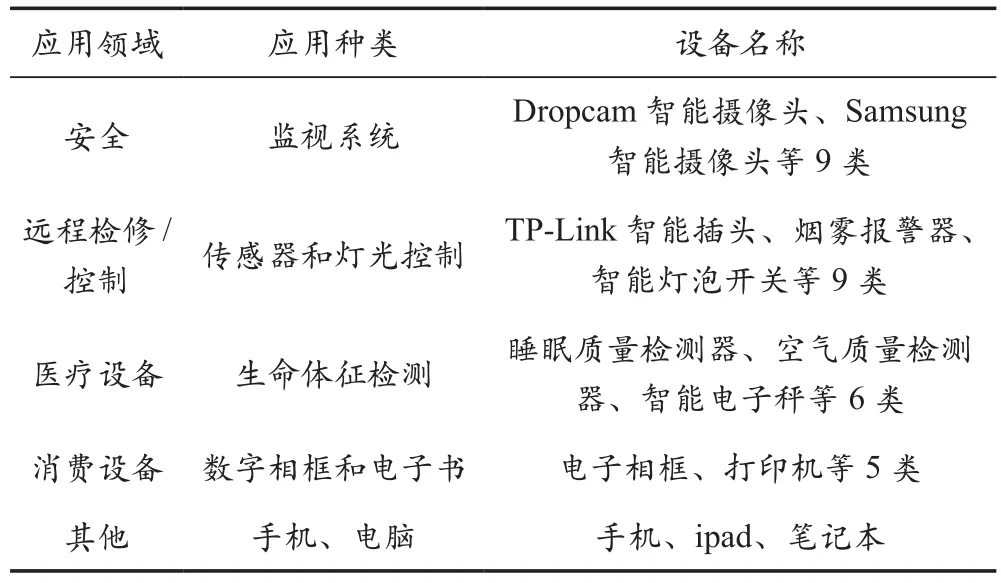
表1 原数据分类

由于实验数据有部分空值和脏数据，因此首先使用Python对数据进行空值处理和数据清洗工作，然后进行数据集解析，提取出报文到达时间、数据包大小、协议类型等信息，计算报文到达时间间隔，为后续实验做准备。

2 校园物联网流量粗粒度分析

2.1 流量特性直观分析

图1表示每天0:00—24:00的校园物联网流量变化情况，横坐标表示产生的数据包时间（单位：min），纵坐标表示每分钟到达数据包的平均个数。可以看出，流量产生的高峰期位于12:00—18:00，出现了凸起的脉冲，其余时间段的流量数据较为稀疏。

图1 物联网流量变化图

对比图2中白天和夜间的流量，流量均呈现出非线性变化，并有明显突发性。夜间流量突发性相对较弱，这是由于物与物之间的通信包括部分周期性数据包，如状态数据采集等与人类活动无关的行为，而白天是用户活动最频繁的时间，会造成网络流量在较大时间跨度上出现强烈波动。

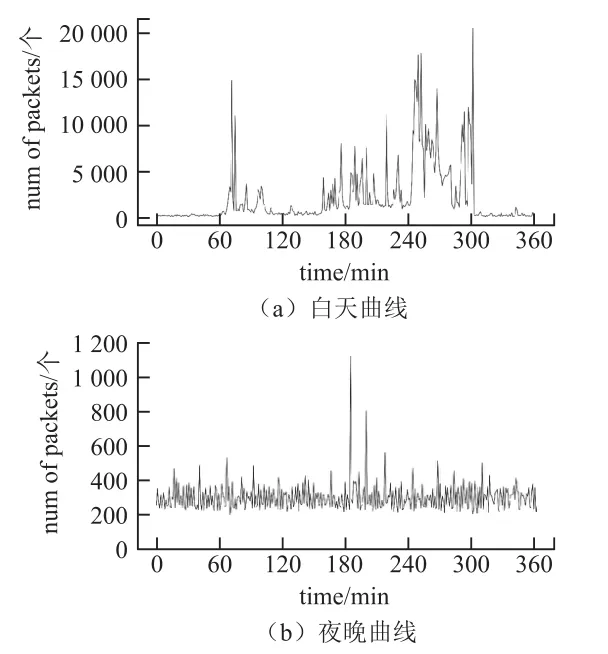
图2 物联网流量曲线

2.2 周期性分析

物联网的流量行为往往复杂多变，数据中含有多种周期类波动。自相关函数（ACF）是测量时间序列中每隔k个时间单位（Δt和Δt-k）间的相关性[6]。如果每隔相同的滞后阶数，且自相关系数是局部最大值，那么该时间序列就具有周期性，且局部最大值间的固定间隔就是周期。

图3所示为校园物联网流量的ACF图，横坐标表示时间（单位：h），纵坐标表示自相关系数。可以看出，约每隔24 h就会出现局部极大值，表明物联网流量具有日周期性。物联网环境中包含多种M2M设备，每种M2M类型的流量具有不同的触发机制和周期间隔，而用户网络活动大多集中在白天，导致聚合流量在小时间范围内不具有周期性。

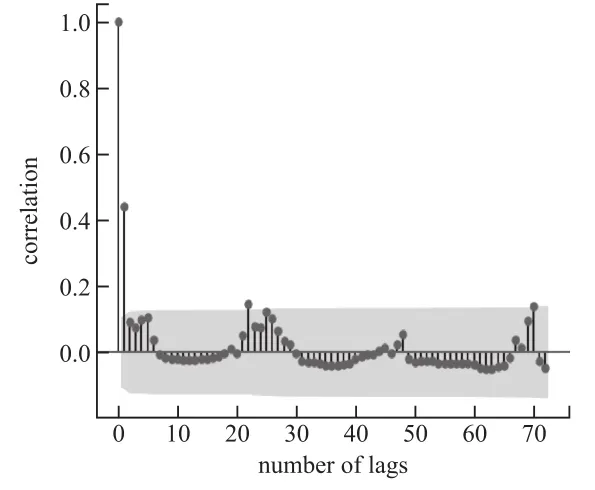
图3 物联网流量ACF图

2.3 稳定性分析

图4所示为物联网流量的偏自相关函数（PACF）图。结合图3可知，ACF在lag=2，PACF在lag=3之后便落入置信区间，表明自相关系数和偏相关系数均迅速衰减到0附近，故初步判定该时间序列具有稳定性。

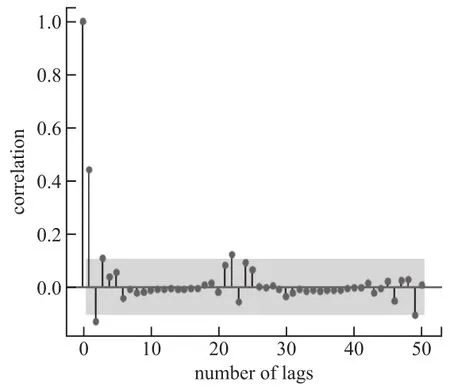
图4 物联网流量PACF图

将校园物联网流量分为M2M流量、互联网流量，结合单位根检验法（ADF）、变异系数法（CV）两种方式来综合衡量报文到达时间间隔的稳定性。

稳定性分析参数见表2所列。采用ADF计算的t-statistic（t）值远小于1%，5%，10%三种置信度的临界统计值，且p-value无限接近于0，说明校园物联网流量具有稳定性；纵向对比3种流量，稳定性程度由大到小分别是总流量、M2M流量、互联网流量。M2M设备产生的流量中既包含定期采集数据的流量，又包含交互流量。周期性使得流量在大时间尺度上显得比较平滑，掩盖了流量的突发性。

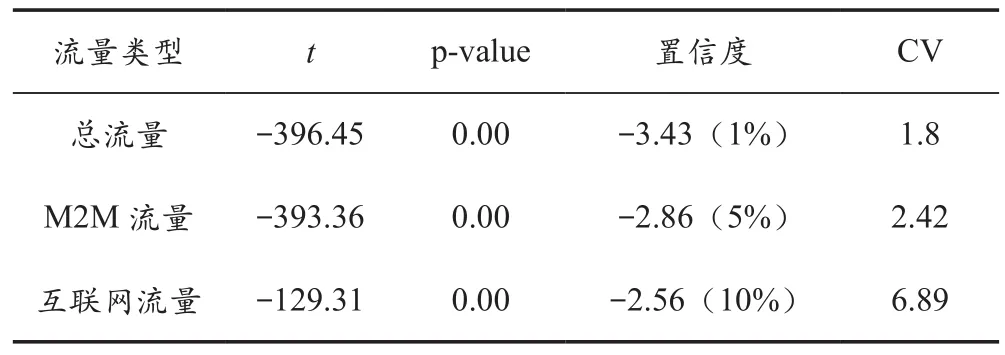
表2 稳定性分析参数

3 校园物联网流量特性细粒度分析

3.1 自相似特性分析

3.1.1 自相似特性的定义与估算

自相似过程的定义：一个连续随机过程{X(t),t∈R}，若满足a>0，对于任何d≥1，公式（1）始终成立，则我们可以称X(t)是具备自相似系数Hurst（H）的自相似过程。

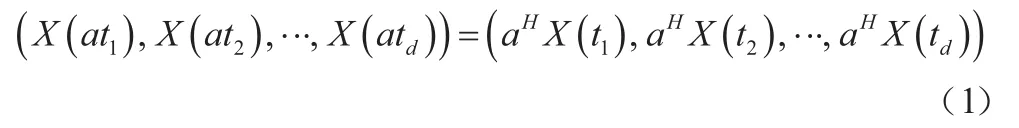
Hurst指数是衡量流量是否具有自相似特性的关键参数。目前估计Hurst参数的方法可大致分为时域算法和频域算法两类。时域算法主要包括：R/S法、留数法、方差时间图法、绝对值法等；频域算法主要包括：Whittle法、小波变换分析法（Wavelet）[7]。综合各种计算方法的准确性和复杂性，本实验采用R/S法来估计Hurst参数。

3.1.2 校园物联网流量自相似特性分析

本实验使用R/S法对网络流量的数据包到达时间间隔和数据包的长度进行Hurst参数估算，实验结果见表3所列。报文到达时间间隔和每秒到达的数据包长度的Hurst参数估计值均大于0.5，表明校园物联网流量具有自相似特性。

表3 Hurst参数估值

3.1.3 不同传输协议的自相似性

传输层协议是导致网络流量表现出自相似性的重要因素之一[8]。按照数据协议类型对数据分类，并分别使用到达时间间隔和数据包长度数据来计算Hurst参数，结果见表4所列。TCP流量的占比相比传统互联网流量[5,9]有所减弱，而UDP协议的流量明显增加。ICMP协议流量的Hurst值始终小于0.5，不具有自相似特性；其余协议流量Hurst参数均大于0.5，具有自相似特性。其中，TCP协议流量的Hurst值始终大于0.8，说明其具有较强的自相似特性。

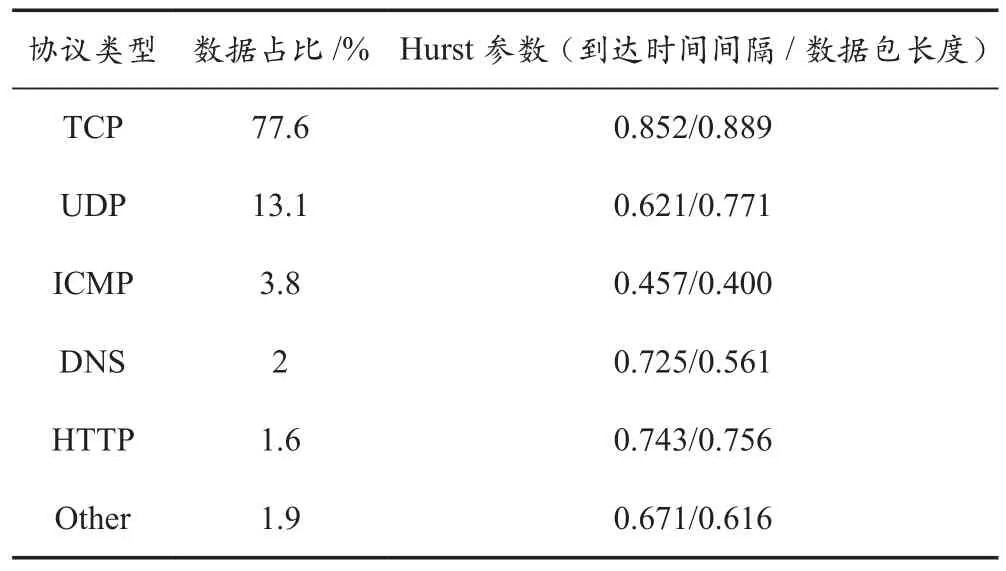
表4 不同传输协议的Hurst参数估值

3.2 校园物联网流量重尾特性分析与拟合

3.2.1 校园物联网流量重尾特性分析

在网络特性的研究中，重尾现象随处可见，当连续事件间存在长时间的等待现象时，则满足重尾分布的特点[10]。

概率密度计算：设样本值为N，区间长度为Δt，统计落在(Δt, (i+1)Δt)的样本数量ni，ni与总样本数N之间的概率计算见公式（2）：

将校园物联网流量分为M2M流量、互联网流量，分别使用公式（2）计算报文到达时间间隔（单位：s）落在每一个子区间的概率，报文到达时间间隔与对应的概率如图5所示。图中横坐标为报文到达时间间隔，纵坐标为横坐标对应概率的对数值。由图5可知，两种流量均具有明显的重尾现象。此外，M2M流量的分布具有明显的分段现象，表明M2M流量具有多尺度特性。

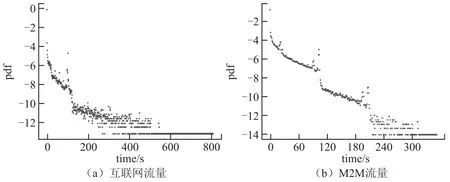
图5 流量概率密度图

3.2.2 校园物联网流量重尾特性拟合

图6刻画了物联网流量的基本特性，横坐标表示数据包到达时间间隔（单位：s），纵坐标表示概率密度函数，用来描述对应时间间隔的概率。通过5种典型的重尾分布进行对比，其中，紫色实线为帕累托（Pareto）分布拟合曲线，绿色虚线为幂律（Power-law）分布拟合曲线，黄色实线为指数（Exponential）分布拟合曲线，红色虚线为对数正态（Lognormal）分布拟合曲线，灰色虚线为威布尔（Weibull）拟合曲线，蓝色圆点为物联网流量报文到达时间间隔的概率。由于数据太过密集，不易观察，将图6中的横坐标区间[0，50]和纵坐标区间[0，0.005]进行放大，得到图7。

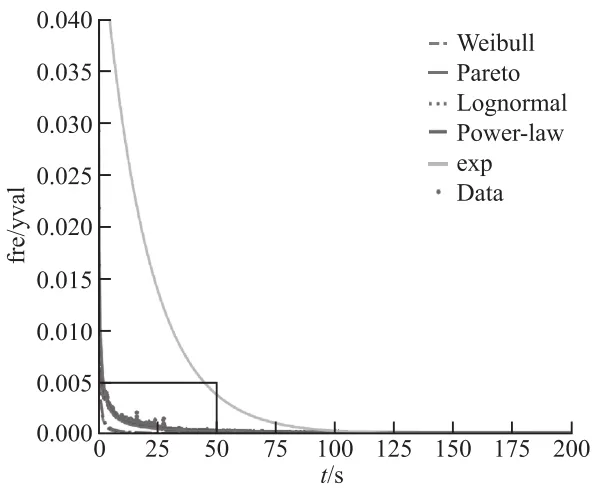
图6 报文到达时间间隔重尾分布拟合完整曲线

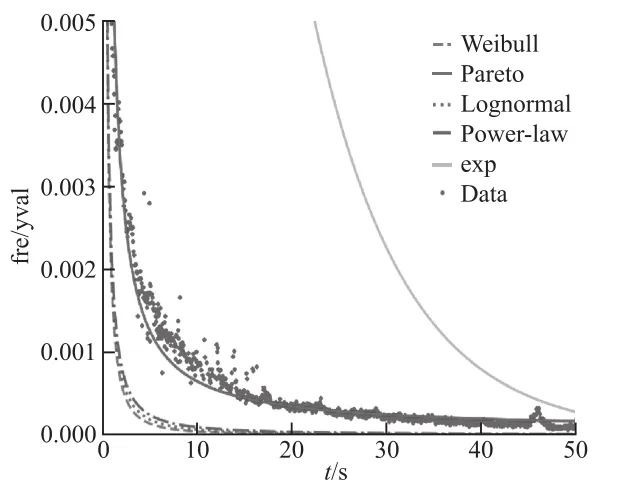
图7 报文到达时间间隔重尾分布拟合局部曲线

选用R2和RMSE的值来反映拟合效果，以选取合适的分布模型刻画流量特性。结合图7和表5可知，拟合效果最佳的是Pareto分布，其拟合曲线经过大部分实验数据点，且其R2值最接近1，RMSE 最小。由此证明，Pareto分布是反应校园物联网报文到达时间间隔变化规律的优质数学模型。

表5 校园物联网流量概率分布模型拟合及评价参数

4 结 语

本文以校园物联网流量为研究对象，从粗粒度和细粒度两个方面对校园物联网流量进行分析。从粗粒度方面研究，发现校园物联网流量具有日周期性、稳定性和非线性等特征。从细粒度方面研究，发现校园物联网流量具有自相似特性，且校园物联网报文到达时间间隔的概率密度函数具有明显的重尾特性和尺度特性。采用五类典型概率分布模型进行拟合实验，对比分析实验结果，评价指标R2和RMSE，确定校园物联网报文到达时间间隔变化规律的最佳模型是Pareto。