自动化立体仓库的可拓策略生成研究

马书美，潘 力，徐俊伟

广东工程职业技术学院，广东 广州 510520

1 自动化立体仓库概述

自动化立体仓库是一种智能化、系统化的集成仓库，集成了运输机、高层货架、巷道堆垛机、仓库控制系统（WCS）和仓库管理系统（WMS）等多个部分，由电子计算机进行管理和控制，实现仓库管理相关的自动化操作。因此，自动化仓库具有高吞吐率、高空间利用率、高周转率和安全性等特点，受到了国内外的广泛关注[1-3]。目前国内大多采用自然堆叠的存储方式，少数具有立体仓库的企业也主要采用大跨度双立柱堆垛机的方式进行存取工作，过度地占用生产空间，同时制约了生产制造效率。国外的立体仓库发展得很成熟，相关的码垛机器人、AGV小车、机械手等已有成套型号设备，尤其是机器人代替人工的智能物流技术快速发展，已经广泛应用于工业上的分拣、包装、装卸、搬运、装配等环节[4-7]。如今，自动仓储行业的快速发展已经为各领域带来了较大的利益，其中最重要的就是货物的分配。常见的分配方式均是单货物作业，即每次运送一个单元的货物（托盘）并存放在一个仓位处。货物分配策略是自动化仓库的关键技术问题[8]。合理地分配货物能够减少很多不必要的工作量，减少仓位堆叠情况，并减少仓库取放和进出不合理的作业，同时提高仓储的工作效率，从而减少劳动力，达到高效率、短周期、低成本、高效益的目的。

近年来，货位优化问题受到了学术界和工业界的高度关注。自动化立体仓库货物分配优化是解决货物位置存放的有效方法。文章主要运用可拓策略生成方法[9-12]，该方法通过模仿人类的思维模式，以可拓学的基本理论为基础，用形式化和定性与定量化相结合的方法生成解决不相容问题的策略。

2 可拓策略生成方法

可拓策略生成方法主要包括建模—拓展—变换—优选四个过程，即通过建立不相容问题的可拓模型，利用关联函数计算问题的相容度以判断问题的矛盾程度，对不相容问题进行拓展分析和变换分析，得到较多的可拓策略，再通过评价选优，选取解决不相容问题的较优可拓策略。其基本步骤如下。

（1）对实际问题界定目标和条件，运用基元理论建立问题的可拓模型。

（2）根据确定的原问题，找到由原问题提供的条件指标和目标指标，获取指标值或者指标取值范围，构建核问题。

（3）建立不相容问题的关联函数，通过计算，判断问题不相容的程度，即是否为不相容问题。

（4）确定目标和条件分析的先后顺序。①当目标不变时，先分析条件，通常选择相关分析方法对条件进行拓展分析，构建相关树或相关网。②当条件不变时，先分析目标，通常选择蕴含分析法对目标进行拓展分析，构建蕴含树。③当两者均变化时，按顺序执行前两步，构建问题的相关蕴含树。

（5）完成上述步骤后，进行发散分析或可扩分析，在此基础上实施可拓变换。变换也具有传导性，因此对树叶到树根变换直到形成变换蕴含树，又被称为可拓策略生成树。

（6）完成问题变换后，根据建立的关联函数对相容度进行计算，若相容度由不大于零变为大于零，则该变换为可行的可拓策略，否则舍弃重新变换。

（7）策略的评价选优。

综上所述，解决不相容问题的可拓策略生成的流程如图1所示。

图1 解决不相容问题的可拓策略生成流程

3 可拓策略生成方法的应用

建立可拓模型的最基本单元包括物元、事元和关系元[9]。物元、事元和关系元统称为基元，基元的一般表示式如下：

其中，B被称为n维基元；对象O代表物、动作或关系词；代表对象O对应的特征；代表对象O的特征对应的量值。

现实世界中，人、事、物之间往往是组合的或复合的。因此，当描述它们之间的组合或复合时，需要用到物元、事元和关系元的复合元形式来表达，统称为复合元[5]，文章主要用到的是事元和物元的复合元。

3.1 建立自动化立体仓库的可拓模型

立体仓库的一般组成部分包括货架、仓位、检测传感器、出入库输送系统[6-7]。此自动化立体仓库主要和机器人配合完成仓储，机器人通过程序分析将物品运送到立体仓库对应的仓位处。其中，货架起到支撑固定作用；仓位起到存放物品的作用；检测传感器一般是在仓位横架处，主要作用是根据此仓位是否有存放物品发送信号给机器人；出入库输送系统主要的作用是辅助机器人及仓库将物品按照信号和运输轨迹准确地传送到对应的仓位处。普通立体仓库三维图如图2所示。

自动化立体仓库存储空间有限，一般是一个仓位存储一个物品，如果物品的体积相对仓位空间较小，可否实现有限的空间多存储呢？文章在现有立体仓库的基础上进行改善，充分利用仓库的空间和仓库的存储功能，得到更优化的货物仓位，使其达到更高的工作效率、实现更大的存储量，即在有限货架仓位的基础上增加存储量。但是，在现有的条件下不能实现有限仓位多存储的目的，因此通过对自动化立体仓库建立可拓模型进行分析。

建立物元模型如下：

建立事元模型如下：

根据物元模型和事元模型可知，立体仓库通过输送机、传感器运用机器人将物品放在对应的无底盘的仓位处。若在已有仓位数的基础上，实现多存储，如何能够达到呢？即限制条件为已知的仓位数n不变，且最终实现多存储的目的。

当前立体仓库是一仓位一物品，若仓位数不变，就需要通过一仓位多物品来实现。根据实际情况，仓位货物分配主要是物品能够合理地放置在仓位处，则需要对仓位、物品的体积进行分析，建立物元模型如下：

由M1、M2物元模型可知，V2≤V1才能够实现物品放置在仓位处，而V1主要由立体仓库的总体积V决定。

3.2 建立自动化立体仓库的关联函数

令一立体仓库的总体积为V，可用体积为V1，由V和V1的关系建立关于V1的关联函数，主要运用初等关联函数[6、9]。

基于提高仓位的存储量，增加物品的存放空间要求，可用体积占比为80%～100%，当实际用的体积占比为可用体积的100%时，属于立体仓库存储利用空间最优的状态。

这些区间可用数轴表示，如图3所示。

图3 区间、、之间的关系

按照杜健[6]定义的初等关联函数、可拓距和位值的计算方法可知

因此，立体仓库“可用体积”的初等关联函数为

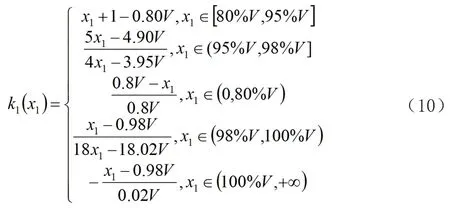
根据x1的取值画出可用体积的关联函数图像，如图4所示。

图4 可用体积的关联函数变化图像

根据x1的取值确定k1(x1)的函数值，函数值越小，则可用体积越小，具体可分为以下几种情况来判断：

（1）当k1(x1)＞0时，可用体积在可接受的范围内；

（2）当k1(x1)≥1时，可用体积在满意范围内；

（3）当k1(x1)=0时，可用体积属于临界，可以改善也可以采取；

（4）当-1＜k1(x1)＜0时，可用体积存在空余，即存储空间造成浪费；

（5）当k1(x1)≤-1时，可用体积存在大量空余，即存储空间造成严重浪费。

4 自动化立体仓库的拓展分析及解决策略

运用拓展分析方法[10-11]中的相关分析方法和发散分析方法分析立体仓库。

4.1 M1的相关分析

根据实际情况可知，立体仓库的可用体积V1与立体仓库本身结构、存放的物品是相互关联的，而影响可用体积的实际利用率的因素或原因是相互影响、相互作用的，即它们之间存在着相关关系。

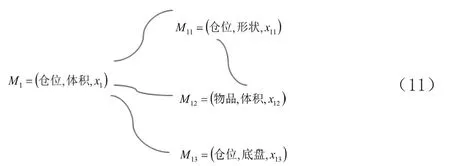
式（11）表示x1的取值随x11、x12、x13的变化而变化，说明M1与M11、M12、M13相关，x12=V2。即有

经过对M1的影响因素进行相关分析后发现，这些因素之间是相互影响、相互作用的。例如，设计的仓位形状为正方体或三棱柱，由于两者的体积不同，会直接影响仓位体积大小；而仓位形状的设计需要考虑存放物品的体积大小，否则会出现物品放不进去或物品放进去会留出大量空余的空间的情况。

4.2 M1相关基元的发散分析

根据第4.1节的相关分析，得到了M1的影响因素和彼此之间的相关关系，要解决在已有的仓位数基础上达到多存储的问题，必须找到这些影响因素的合适的解决途径，需要对这些影响因素的基元进行发散。基元的发散分析可以对基元的对象、特征和量值进行发散，文章结合立体仓库使用的实际情况，以对量值的发散为主。

4.3 M1相关基元可拓变换

由于对M1不能直接进行改善，根据第4.1节的相关分析可知，可以对其相关基元进行改善。

对M1的相关基元实施可拓变换[5，10]，在可拓变换这一过程中，会有多种变换情况，以对M11实施主动变换的3种情况为例。

上述变换与传导变换的结果说明，在设计时，仓位的形状不同求出的体积也不同，会直接影响能够存储的空间和存储的物品数量。例如，物品的体积在仓位体积允许的空间范围内，有时候一个物品存放后有空余，此时可以根据仓位的多元形状（如正方体+圆形）通过机器人判断将另一个符合的物品放入同一仓位的另一形状处，在充分利用空间的同时能够实现整洁有序的一仓多物；仓位是否有底盘在实际使用中也会影响仓位体积的利用率，底盘能够起到支撑和旋转变换角度以随时通过传感器给出剩余体积对应的角度信息的作用，保证每个仓位的体积都能够充分利用。

4.4 利用关联函数获得解决策略

根据以上相关基元的拓展分析，得到了对立体仓库的3种不同的改善策略，在此基础上用立体仓库的关联函数得到最满意的解决策略[12]。

由以上计算出的关联函数数值可知，第二种是最满意的解决策略。

根据第二种可拓策略解决方法，在原来的仓库（如图2所示）的基础上进行优化改善后得到如图5所示的货物仓位分配三维模型。

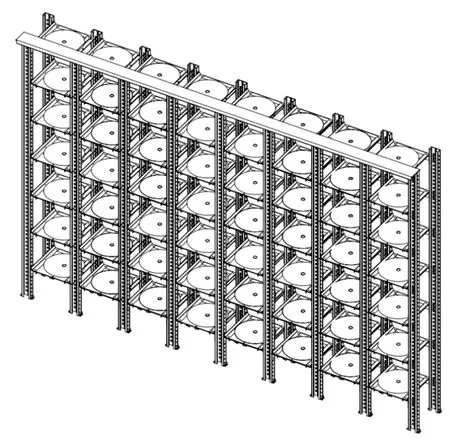
图5 优化后的立体仓库三维图

5 结论

文章主要利用可拓策略生成方法中的建模对自动化立体仓库仓位货物分配优化进行研究分析，对立体仓库的仓位可用体积建立准确化、定量化初等关联函数，利用可拓变换分析仓位的可用体积受哪些主要因素的影响。选取三种解决策略，对这三种解决策略运用自动化立体仓库关联函数计算出每种策略对应的关联度，通过关联度的比较，结合可接受范围和满意范围进行选优，最终选出最满意的解决策略以达到自动化立体仓库多存储、高效率的目的。该方法同样适合生产企业边存储边取物的工作过程。