丁坝挑角对周围流场影响的三维数值模拟研究
2021-12-13胡志毅
胡志毅
西北农林科技大学水利与建筑工程学院,陕西 咸阳 712100
丁坝是河道整治中常见的水工建筑物,可以有效地改变河道的水流结构,对于岸坡防护、水运通航以及提高水生物栖息环境都发挥了积极的作用。但是,坝头处的冲刷也会对丁坝的稳定性产生较大影响。根据丁坝与来流方向交角的不同,可分为上挑型、正挑型和下挑型,而丁坝挑角的不同,对丁坝绕流、坝头冲刷均会产生不同的影响。
20世纪以来,许多学者对坝后回流区展开了相关研究,前期主要是以室内试验为主,而随着近年来计算机科学的发展,数值模拟成为一种新的研究手段。周宜林等[1-2]通过大涡模拟中的SM模型分别模拟了不同挑角下3种非淹没丁坝附近的水流特性,结果表明上挑丁坝附近流态变化最大;下挑丁坝下游所产生平面涡及断面逆向流相对更长,更有利于丁坝坝头和河岸的保护。在实际工程中,从安全和经济方面考虑,应当将丁坝群设置于坝后回流区流速较小处。吴伊平等[3]通过三维数值模拟,深入对比研究了丁坝挑角及长度对坝后回流区流动特性的影响,并对模型试验结果进行了验证。
1 计算流体动力学前处理
1.1 控制方程
研究所涉及的主要控制方程为连续性方程及动量方程,选取RNGk-ε湍流模型,并采用SIMPLEC算法对其进行求解。
1.2 计算域建立及网格划分
采用Zhang等[4]在京都大学开展的模型试验作为算例,水槽试验段长4.0m、宽0.4m、高0.4m,坡度为0.001,糙率为0.009,共划分为定床—动床—定床3个区域,如图1所示。其中,动床段长1.7m,起始端位于试验段下游0.5m处,水槽底部铺设厚度为0.2m的人工沙。丁坝位于水槽右侧,长0.1m、宽0.01m、高0.28m,属于非淹没丁坝。为了保证水流的充分发展,上游进口端距离丁坝2m,试验平均水深0.05m,行进流速为0.29m/s。

图1 计算域布置图(单位:m)
3种模型的计算域均采用混合网格进行划分,其中定床部分采用结构网格,动床区域采用非结构网格,并在丁坝附近进行网格加密,90°丁坝计算域的总网格数为123万个,60°和120°丁坝计算域总网格数均为150万个。
1.3 边界条件设置
(1)进口边界。水流进口处设置为速度进口,初始流速为0.29m/s,水深0.05m;根据以下公式

确定湍动能k=3.1×10-4,ε=2.6×10-4。空气进口以及计算域顶部设置为压力进口。
(2)出口边界。出口定义为压力出口,由于模拟案例属于河道明渠流,因此在VOF模型下需要打开“Open Channel”选项,并在压力出口设置面板中设置出口处的水面高程和基底高程。
(3)壁面边界。河道两侧、底部及坝面均设置为无滑移壁面,并采用标准壁面函数,以求解近壁区的水流流动。
2 模拟结果
2.1 流速场分布
根据各挑角下的丁坝附近流场的数值模拟结果,分别选取近底面z=0.001m、中截面z=0.0025m以及自由水面z=0.05m 3个断面处的速度分布云图以及流线图进行比较分析,如图2~图4所示。

图2 60°挑角速度分布云图

图3 90°挑角速度分布云图

图4 120°挑角速度分布云图
由速度分布云图可以看出,当水流行近至丁坝前侧,部分水流由于丁坝的阻水作用,形成坝前滞留区,流速也相对较小。在120°挑角下,由于滞留区内的水流流动受到丁坝的限制,无法向下游发展,因此形成了小范围的坝前回流区。靠近丁坝对岸的主流区水流流向几乎不受丁坝影响,沿原方向继续向下游发展,但由于过流面积减小,主流收缩导致流速明显增大;靠近坝头处的水流则形成绕流,由于惯性作用,主流宽度继续收缩,随着主流的逐渐扩散,主流与丁坝正后方的静压区的剪切层作用,形成坝后回流区。由流线图可以看出,回流区内的水流回流至坝后时,由于丁坝的阻挡,在坝后形成了小规模、逆时针漩涡。由于60°挑角丁坝沿水流方向投影长度最大,因此该漩涡的规模相比90°、120°挑角更大。
同时,在同一挑角下,近底面的平均流速明显小于其他断面,这是由于z=0.001m断面处于黏性底层内,且壁面属于紊流粗糙面,因此该区域水流受壁面摩擦阻力以及黏性阻力的影响较大,故速度较小。随着水深的减小,水流进入紊流核心区,水流流速在垂直方向呈对数分布规律,平均流速逐渐增大。
此外,不同挑角下相同水深处的速度分布规律基本一致,其中60°、90°以及120°挑角对应的流速最大值分别为0.497m/s、0.523m/s和0.512m/s,最大流速与挑角呈先增大后减小的关系。60°、90°及120°挑角对应的回流区长度分别为1.14m、1.11m和1.13m;最大回流宽度分别为0.157m、0.16m和0.158m。由此可见,挑角对于坝后回流区范围几乎没有影响。
2.2 回流范围验证
为了验证回流区范围的合理性,通过李国斌等[5]建立的非淹没丁坝下游回流区长度及最大宽度公式进行对比。其公式为
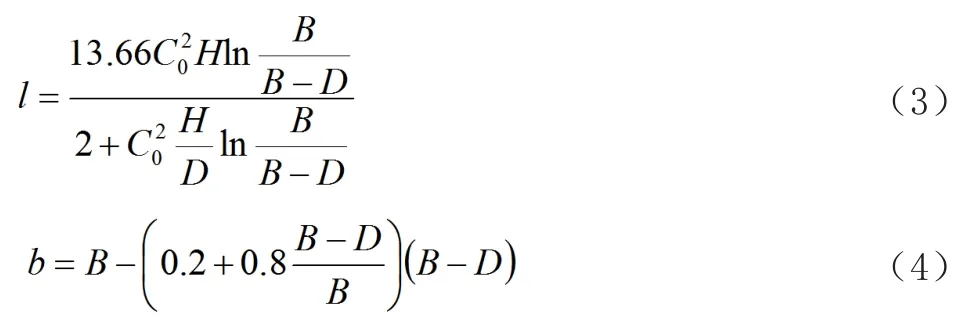
式中:l为回流区长度;b为最大回流宽度;D为坝长;B为水槽宽度;H为水深;C0为无量纲谢才系数。
将相应参数代入计算,可得l=1.28m,b=0.16m,则数值模拟计算结果为l'=1.13m,b'=0.158m,相对误差分别为11.7%和1.3%。由此可知,所得模拟结果精度较高[6]。
3 结论
(1)相同挑角下,丁坝附近的平均流速随着水深增大而减小;不同挑角下的速度分布规律基本一致,其中90°丁坝的最大流速相比其他两个挑角更大。
(2)不同挑角的坝后回流区范围基本一致,将90°挑角丁坝坝后回流范围与相关公式计算结果进行对比,可得回流长度相对误差为11.7%,回流宽度相对误差仅为1.3%,验证了所得模拟结果的准确性。
