自冲铆接三层板工艺参数对接头质量的影响探究*
2021-12-13杜爱民韩业扬陈垚伊孟宪明
杜爱民,韩业扬,陈垚伊,孟宪明,吴 昊
(1.同济大学 汽车学院,上海 201804;2.中国汽车技术研究中心有限公司,天津 300300)
1 SPR概述
SPR是一种冷连接工艺,用于固定2层或2层以上的材料。SPR可用于紧固各种材料,包括钢、铝、尼龙织带、塑料和橡胶等。它的工作原理是将一个典型的半管状铆钉推入材料的目标堆中,在此期间材料和铆钉的塑性变形使得材料堆内形成机械锁[1]。SPR过程中涉及到的零件有冲头、铆钉、板料、凹模,零件的工艺参数之间相互影响,是SPR工艺产品质量的重要影响因素,所以对SPR技术的研究主要集中在零部件的工艺参数上面,探究工艺参数对铆接接头的疲劳性能和力学性能等方面的影响[2]。三层板的工艺参数包括凹模半径、凹模深度、铆接速度、铆钉长度、铆钉腿部圆弧半径等。三层板的搭接形式能够搭接多种不同的材料,满足在生产制造过程中的更高铆接接头性能需求,因此具有广阔的应用前景。工艺参数对SPR的工艺产品性能影响较大,相对传统的两层板工艺,三层板工艺涉及更多的工艺参数影响,每层板的工艺参数对整体三层板的单因素和交互因素的影响各不相同,且各工艺参数对性能指标的影响存在耦合关系,因此针对实际使用的铆接性能需求,选取合适的工艺参数对于SPR工艺提升极其重要。目前,国内外已有一些研究机构和学者进行了SPR工艺优化方面的研究。
2009年,闫哲铭[3]提出随着铆接板料总厚度增加,需要的铆接力增加,在铆接时穿透上层板料所需的铆接力取决于上层板料厚度,而与下层板料厚度无关。随着下层板厚度的增加,铆钉穿过下层板的行程和所需的最大铆接力都会增加。所以,在铆接总厚度较厚或者单层板料较厚时,选择高硬度的冲头和模具可以减少SPR设备的损坏。2015年,邓成江等[4]提出,由于三层板材搭接形式的不同,使得三层板搭接自冲铆的拉伸剪切和剥离强度不尽相同,以至于其失效形式及能量吸收也不相同。2017年,邰加琪等[5]认为采用拉伸-剪切连接方式(见图1)或者增加板料宽度能提高接头的静强度和宽度。

图1 拉伸-剪切连接方式
Han L等[6]在研究三层板搭接形式时,选用AA6111+NG5754+NG5754 3种板料在不同的搭接形式下测量接头的拉伸、剪切强度。发现图2所示的S3型搭接形式下的接头强度最高,并且在拉伸过程中吸收的能量最多。

图2 三层板拉伸-剪切布局形式示意图
从研究现状可以看出,国内外的研究主要针对两层板的SPR过程,旨在通过优化SPR过程的工艺参数对接头性能进行提高。三层板的SPR研究较多集中在板材类型和组合布局形式的优化上,三层板SPR工艺参数方面的研究较少,针对三层板及更多层的SPR过程进行工艺参数对于未来的生产制造意义重大。因此,本文主要基于响应面方法设计8 mm三层板性能仿真试验,合理选择工艺参数,探究不同工艺参数对SPR产品性能的单因素及交互因素影响。
2 试验原理
响应曲面设计法是指通过试验的方式获得试验的因素和目标值,对因素和目标值进行多元非线性回归方程拟合并获得拟合方程的方差分析,通过对所拟合的方程进行多元多目标优化分析获得最佳的因素值即工艺参数。由于是多元非线性回归方程,每2个因素之间可以形成一个响应曲面,所以称为响应曲面设计法[7]。
中心复合试验设计(Central Composite Design,CCD)与Box-Behnken试验设计(Box Behnken Design,BBD)[8]是响应曲面设计法的2种具体形式。
CCD又称为二次回归旋转设计,是两水平因素试验的拓展,其试验设计序惯性是通过增加因素的水平数量实现的。CCD在两水平因素试验点的基础上增加轴点和零水平的中心试验点构成,具有设计简单、预测型号、试验次数少等优点。CCD的组成包括3部分:立方试验点、轴向试验点和中心试验点。
不同于CCD试验,BBD不需要连续进行多次试验,并且在因素相同时,BBD试验次数更少,因而更加经济。BBD是一种球面设计,所有的试验点都位于球面外切正方体边的中点(见图3)。
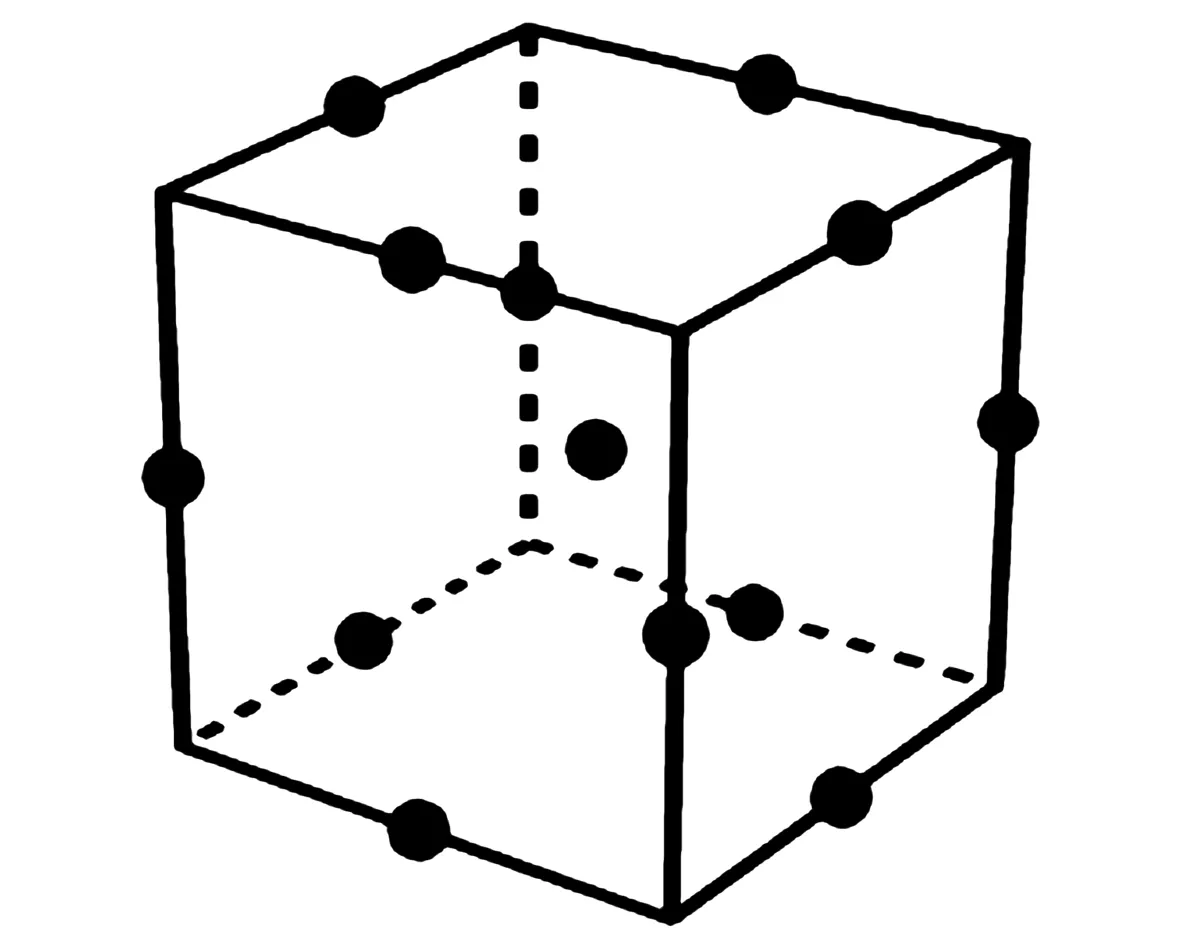
图3 BBD试验设计点
CCD的因素个数一般为2~6个,BBD的因素个数一般为3~7个,当进行3~7个因素的试验设计时,两者需要完成的试验次数见表1。

表1 CCD和BBD试验次数对比
根据以往的研究可知,自冲铆接试验的工艺参数与接头强度之间的函数关系是非线性的[9]。本文待优化的因素为铆钉长度、凹模直径、凹模深度、铆接速度以及铆钉腿部圆弧半径,因素的个数在5个以内且均可以量化。由上述条件可知,自冲铆接三层板试验符合响应面设计的特征,故可使用响应曲面的方法进行设计。相比CCD响应曲面设计,BBD有2个显著的优点:不需要连续进行试验和轴向点在实际试验中不会超出安全范围。
3 试验方案
由于本次试验的工艺参数较多,所需试验次数较大,BBD试验设计的经济性更好,同时为确保试验参数都在安全的范围内,选择BBD试验设计原理。
为提升三层板铆接接头的拉伸性能,试验所用8 mm三层板的各层厚度分别为2.5、2.5和3 mm,基于该厚度组合方式进行工艺参数优化。
选择凹模的半径R1、深度H、铆接的速度V、铆钉的长度L和腿部圆角半径R2共5个工艺参数作为待优化参数。工艺参数的优化范围见表2。

表2 待优化参数范围
选择自锁量、最小底部厚度和最大抗拉伸力作为优化指标。通过BBD试验原理共设计了46次试验,试验方案和试验结果见表3。

表3 试验方案和结果
4 试验结果与分析
三层板工艺参数响应面的试验结果包括两部分:1)各工艺参数和目标值之间回归方程的拟合;2)各工艺参数对目标值的影响。拟合方程的好坏程度由方差分析表得出,工艺参数对三层板目标值的影响由各响应面体现。
4.1 自锁量回归模型
自锁量的二次非线性回归模型如下:
L(x)=20.348 77-1.741 9x1-3.271 21x2-
0.001 258x3-2.600 88x4+3.032 99x5+
0.035 897x1x2+0.000 085x1x3+0.134x1x4-
0.038 667x1x5+0.000 453x2x3+0.295 385x2x4+
0.366 923x2x5+0.000 094x3x4-0.000 644x3x5-
(1)
式中,L(x)为自锁量;x1为凹模半径;x2为凹模深度;x3为铆接速度;x4为铆钉长度;x5为铆钉腿部圆弧半径。
由方差分析表(见表4)可知,自锁量二次回归模型的P值<0.01,回归模型是显著有效的。

表4 自锁量回归模型方差表
4.2 最小底部厚度回归模型
最小底部厚度适用于线性模型,其回归方程模型如下:
H(x)=2.850 32-0.152 417x1-0.576 923x2+
0.000 042x3-0.077 375x4+0.416 75x5
(2)
式中,H(x)为最小底部厚度。
由方差分析表(见表5)可知,最小底部厚度线性回归模型的P值<0.01,回归模型是有效的。
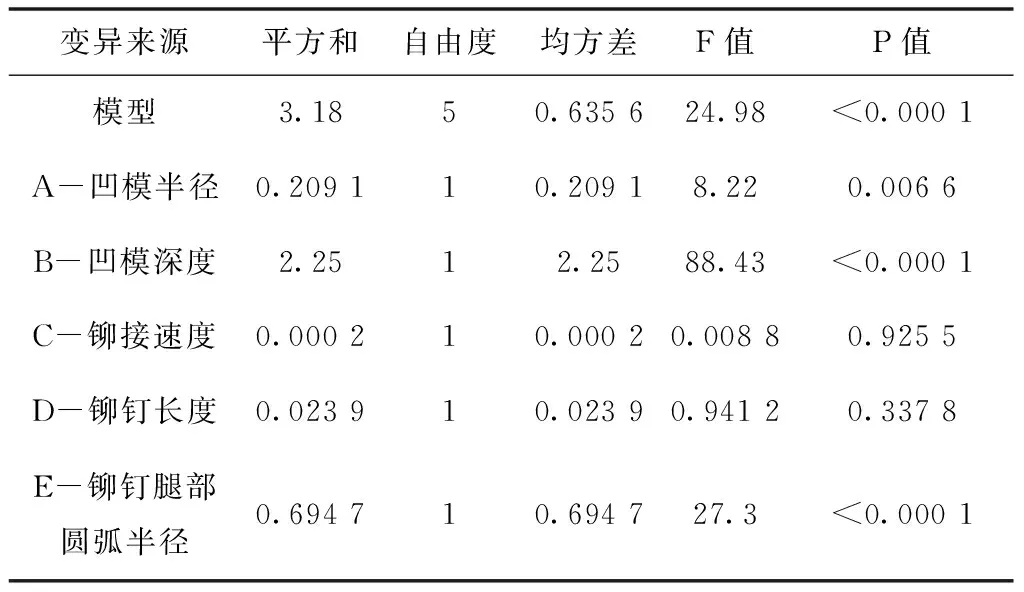
表5 最小底部厚度回归模型方差表
4.3 拉伸力回归模型
对于拉伸力适用于线性模型,其回归方程如下:
F(x)=5.215 37+0.310 598x1-0.042 829x2+
0.000 855x3-0.297 91x4-0.140 33x5
(3)
式中,F(x)为最小底部厚度。
由方差分析表(见表6)可知,拉伸力线性回归模型的P值<0.01,回归模型是显著有效的。

表6 拉伸力回归模型方差表
4.4 单因素对目标值的影响
图4所示为单因素变量如凹模半径、凹模深度、铆接速度、铆钉长度和铆钉腿部圆弧半径对自锁量的影响。
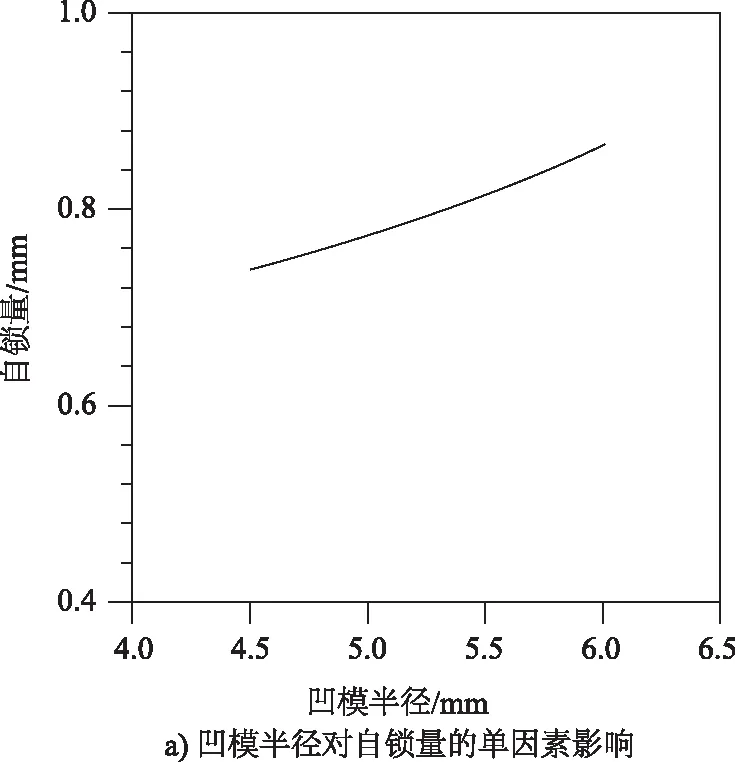
图4 自锁量单因素分析
由图4可知,铆接的速度对自锁量影响不大,铆钉的长度和凹模的半径对自锁量有正相关的影响,凹模深度对自锁量的影响为负,铆钉的腿部半径对自锁量的影响先增加后减小。
图5所示为单因素变量如凹模半径、凹模深度、铆接速度、铆钉长度和铆钉腿部圆弧半径对最小底部厚度的影响。

图5 最小底部厚度单因素分析
由图5可知,铆速和铆钉长度对最小底部厚度影响不大,铆钉腿部圆弧半径对最小底部厚度有正相关影响,凹模的半径和深度对最小底部厚度的影响为负。
图6所示为单因素变量如凹模半径、凹模深度、铆接速度、铆钉长度和铆钉腿部圆弧半径对拉伸力的影响。
由图6可知,铆钉的长度和腿部圆弧半径对拉伸力的影响为负,凹模的半径和铆速对拉伸力影响为正,凹模的深度对拉伸力的影响不大。
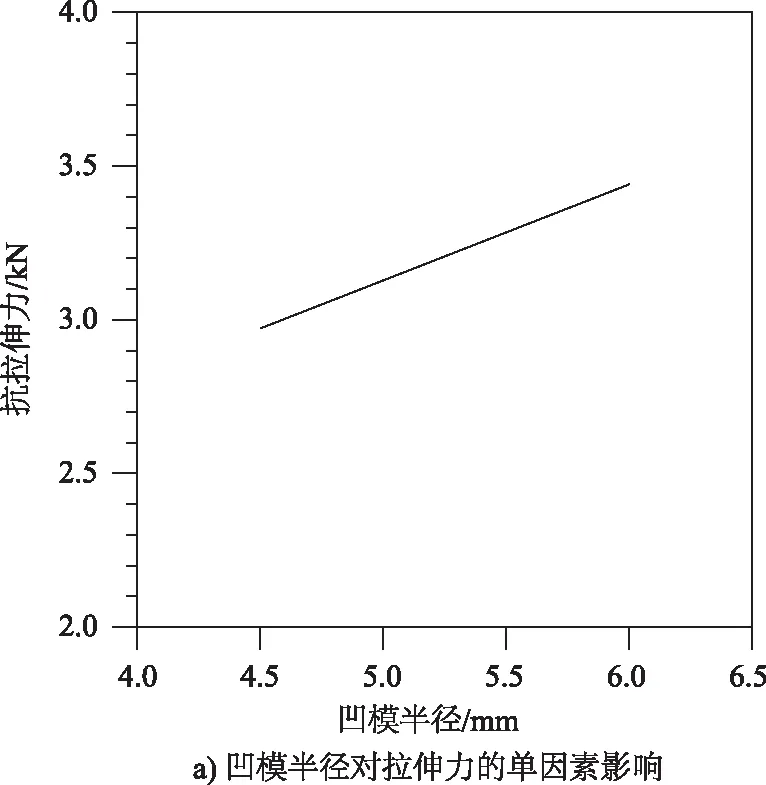
图6 拉伸力单因素分析
4.5 交互因素对自锁量目标值的影响
由于自锁量回归模型采用的是二次方程模型,所以需要分析交互自变量对自锁量的影响。由于铆速对自锁量影响不大,铆速和其他因素的交互影响约等于其他因素的单因素影响,故不再考虑铆速的交互作用。主要考虑AB、AD、AE、BD、BE、DE这6个交互因素的影响。图7~图12所示为交互作用对自锁量的影响。
图7所示为凹模半径和深度对自锁量的交互作用,半径更大和深度较低的凹模会得到更大的自锁量。图8所示为铆钉腿部圆弧半径和凹模半径对自锁量的交互作用,当铆钉腿部半径为1.6~1.8 mm时,自锁量较大,且随着凹模半径的增加自锁量也会增加。图9所示为铆钉长度和凹模半径对自锁量的交互作用,选择大半径和较长的铆钉有助于获得更大的自锁量。图10所示为铆钉长度和铆钉腿部圆弧半径凹模半径对自锁量的交互作用,选择铆钉长度>11.8 mm,且铆钉腿部半径为1.6~1.8 mm有更大的自锁量。图11所示为铆钉腿部圆弧半径和凹模深度对自锁量的交互作用,当铆钉腿部圆弧半径为1.6~1.8 mm,且凹模的深度较浅时有更大的自锁量。图12所示为铆钉腿部圆弧半径和凹模半径对自锁量的交互作用,铆钉长度为11.4~12 mm时,随着凹模的深度增加,自锁量增加。

图7 凹模深度和凹模半径对自锁量的交互作用

图8 铆钉腿部圆弧半径和凹模半径对自锁量的交互作用
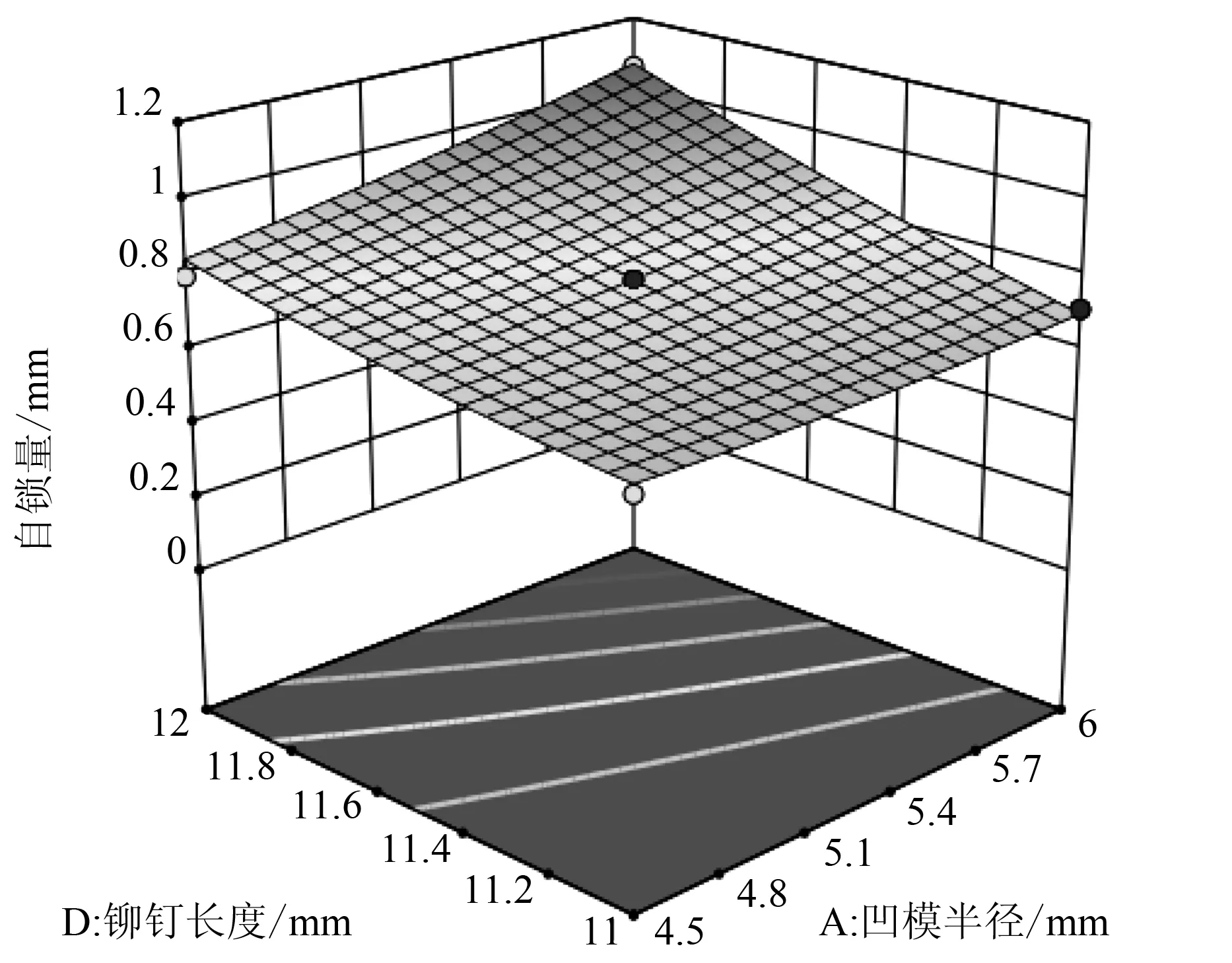
图9 铆钉长度和凹模半径对自锁量的交互作用
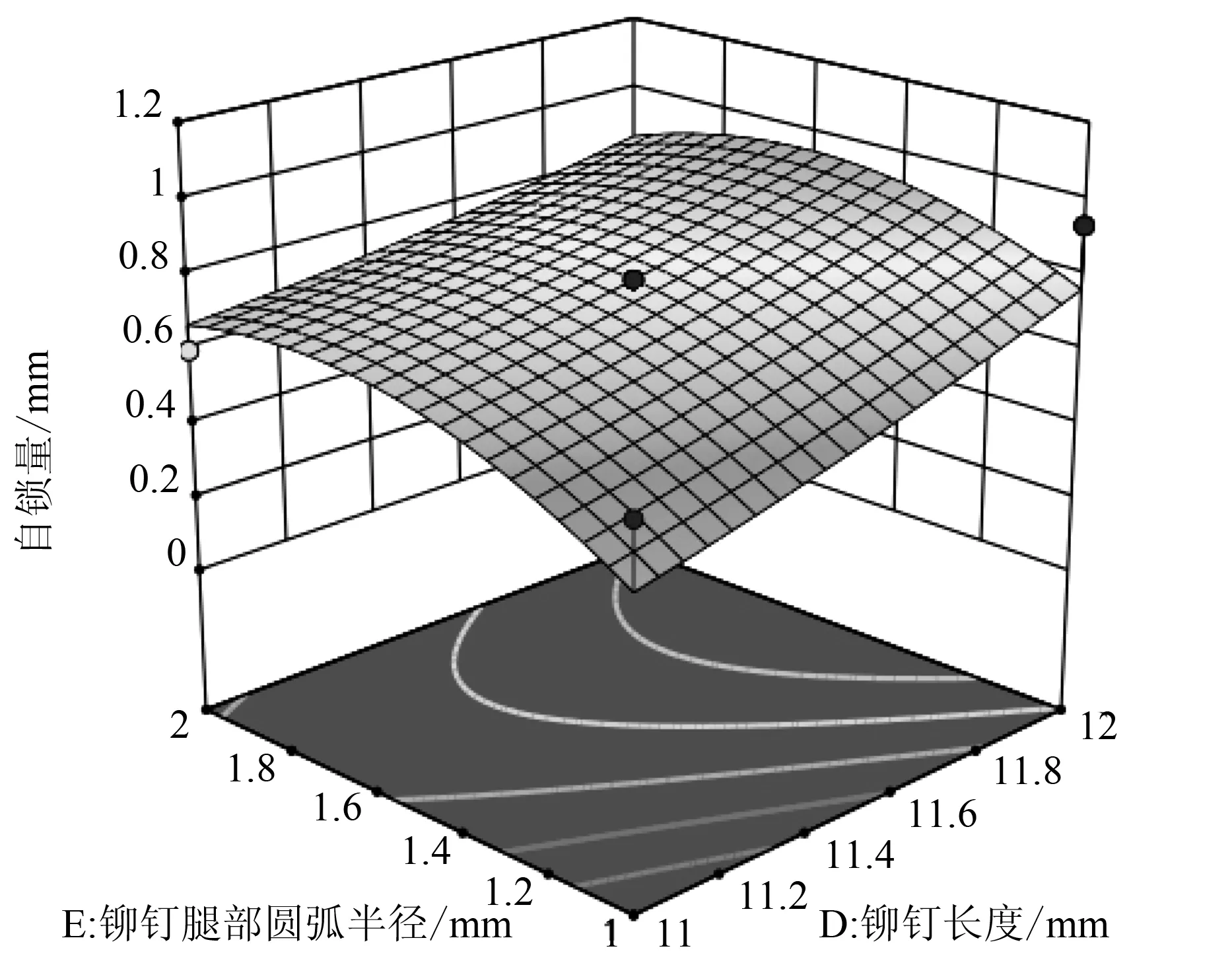
图10 铆钉腿部圆弧半径和铆钉长度对自锁量的交互作用
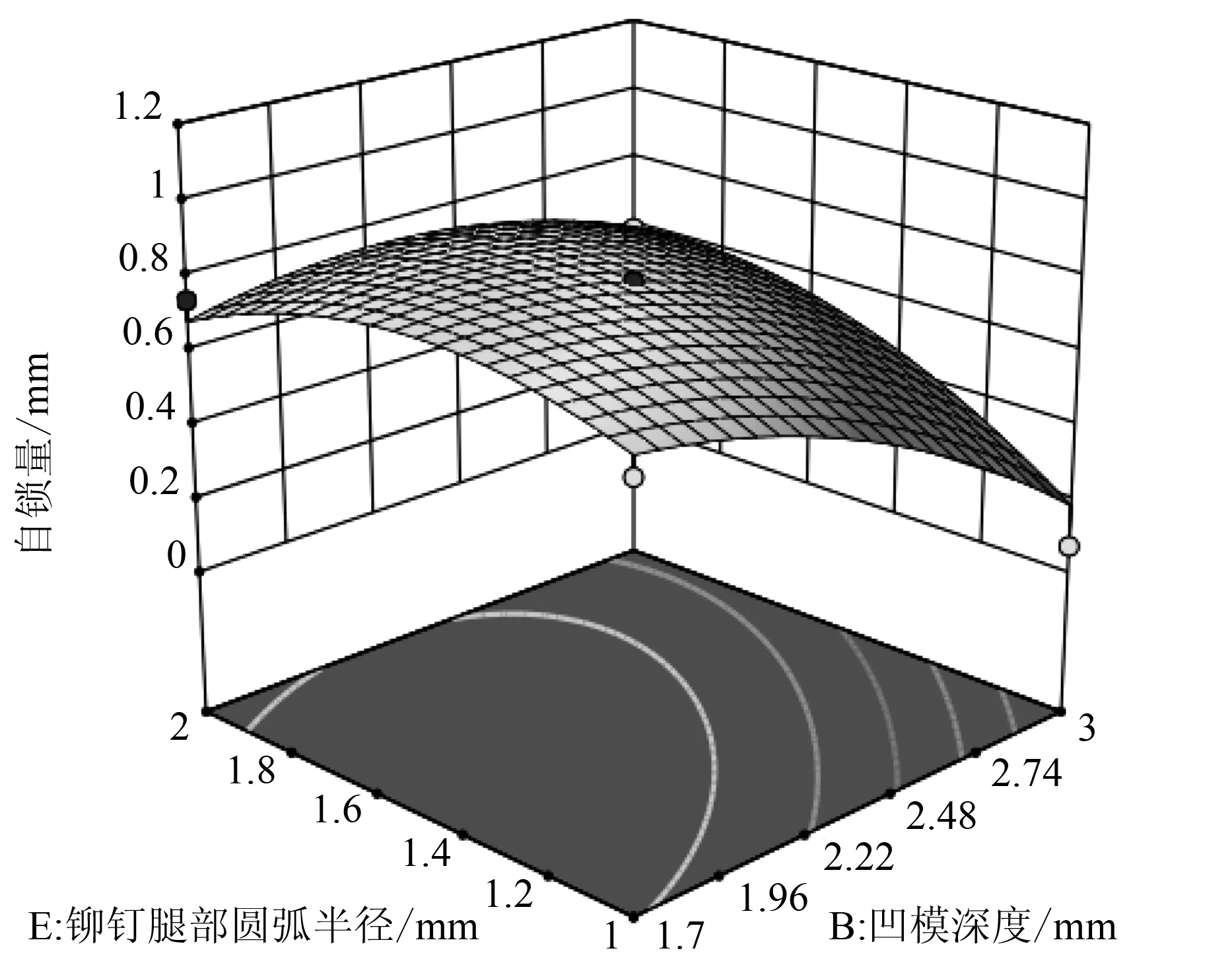
图11 铆钉腿部圆弧半径和凹模深度对自锁量的交互作用

图12 铆钉长度和凹模深度对自锁量的交互作用
综上所述,选择大半径、低深度的凹模,11.8 mm以上且铆钉腿部半径为1.6~1.8 mm的铆钉能够获得更大的自锁量。
5 结语
本文利用响应曲面分析中的BBD试验设计原理共设计了46组自冲铆接和拉伸破坏试验,对凹模半径、凹模深度、铆接速度、铆钉长度、铆钉腿部圆弧半径共5个工艺参数进行优化分析,优化指标为自锁量、最小底部厚度和拉伸力。建立了自锁量的二次非线性回归方程,最小底部厚度和拉伸力的线性回归方程。并分析了单因素及交互因素对三层板优化指标的影响,为后续的参数优化打下了试验基础。
