优化Huber选权迭代法的墙面平整度分析

李 杨

(江苏省基础地理信息中心，江苏 南京 210009)

1 概述

在现实世界中,许多物体的形状是规则的平面,如建筑物的墙面、路面、幕墙玻璃面等[1]。建筑墙面平整度是指墙体表面凹凸不平及厚薄不均的程度，在建筑物施工、验收和变形观测等方面常常需要确定墙面平整度[2]。针对建筑物墙面平整度的检测，传统的方法是利用2 m靠尺和楔形塞尺相结合进行检测，但是随着建筑行业的发展，这种方法已经不适应新形势下对墙面平整度的检测要求。现阶段通常利用免棱镜全站仪，通过工程实例，对建筑物主体外墙墙面平整度进行了观测，并应用平面拟合的方法对建筑物墙面平整度进行了拟合运算，最终推算出墙面整体的平整度。在本文中，利用三维激光扫描仪对墙体进行三维激光扫描，相对于传统测量工具，其速度快，不需要接触被检测物体。它可以快速获取大量的墙面点云数据，节约现场作业时间[3-6]。针对墙体的点云数据，提出一种优化的Huber选权迭代方法，利用该方法对点云数据进行最小二乘拟合，使得墙面拟合多项式更优化，获得精确的墙面拟合多项式，进而得到墙面整体的平整度。该方法相对于传统的墙面平整度的测量方法，更具有整体性，同时在原有的基础上能够有效的抵抗粗差的影响，极大程度的提高墙面平整度测量的精度[7-9]。

2 引入RANSAC算法思想的Huber选权迭代法

由于三维激光扫描过程中，存在粗差，会影响墙面拟合的精度，从而影响墙面平整度的检测可靠性[10-11]，所以在墙面拟合时，需要对粗差进行改正，本文提出了一种Huber选权迭代的优化方法，在Huber选权迭代的基础上引入RANSAC算法思想，利用该方法对预处理后的点云数据进行处理，剔除粗差超过一定范围的点数据，优化拟合平面。RANSAC算法(Random Sample Consensus)即随机抽样一致性算法。该算法通过迭代的计算方式，可以从包含“局外点”的数据中，通过设定阈值筛除一些误差较大的点，从而估计出正确的模型参数。加入RANSAC算法思想后的优化权函数形式如下：

其中,Pii为权阵对角线元素；V(i)为第i个观测值残差；c为常数项(本研究中c取0.1)；当残差的绝对值小于2δ时，Huber即为最小二乘估计，当残差的绝对值大于2δ且小于3δ时，权与残差成反比，残差越大，其权越小，影响也越小，此法是属于有淘汰区的M法，以3δ为极限误差，当残差的绝对值大于3δ时，将其理解为超限值，并将相应的点云数据进行删除。利用此函数进行迭代计算，使粗差的权越来越低，从而减轻粗差对实验的影响。

3 基于优化Huber加权迭代法的平整度计算过程

将三维激光扫描仪安置在房间的中心位置处，对整个墙体进行扫描得到点云数据，扫描得到的点云数据如图1所示。

由于平整度的研究不需要绝对定位，所以就不需要与国家控制点进行联测。将扫描得到的点云数据导入仪器配套的点云处理软件中，对点云数据进行预处理(点云去噪、过滤)，进而将点云数据格式转换为.xyz坐标文件，将.xyz文件更改为MATLAB可识别文本格式，然后利用MATLAB软件对坐标文件进行平面模拟，最终计算得到墙面平整度数值，并对每个点到拟合墙面的距离进行统计分析。具体计算步骤如下：

从坐标文件中任选三个不共线的点P1(x1,y1,z1),P2(x2,y2,z2),P3(x3,y3,z3)，根据这三个点可求出一个初始墙面方程为：a0x+b0y+c0z+1=0，假设真实墙面的平面方程为：ax+by+cz+1=0。根据测量平差中的间接平差原理，每个点云数据的误差方程为：

4 墙面平整度分析

本文中扫描墙体为抹灰墙面，使用的仪器为：HS650扫描仪。采集到的点经过去噪处理后共有4 092个点，在HD_3LS_SCENE软件中将点云数据进行格式转换，转换为.xyz坐标文件，再利用MATLAB软件对坐标文件读取，将上述的Huber选权迭代优化权函数利用MATLAB编写为相应的程序，代码如下：

fori=1∶n

if abs(V(i))≤2*sigma

P(i,i)=1;

elseif 3*sigma≥abs(V(i))>2*sigma

P(i,i)=0.1/abs(V(i));

else

P(i,i)=0;

end

end

P;

利用上述函数，在迭代过程中将部分粗差(即改正值大于三倍中误差的值)较大的点云数据删除，优化了点云数据的质量，处理后点云数据还剩下3 829个点，再利用MATLAB进行墙面拟合，拟合的多项式为：0.225 7x-0.093 2y+0.079 9z+1=0。计算每个点到墙面拟合式的距离并绘制成图，图2，图3分别为改进前后墙面点到拟合平面的距离。

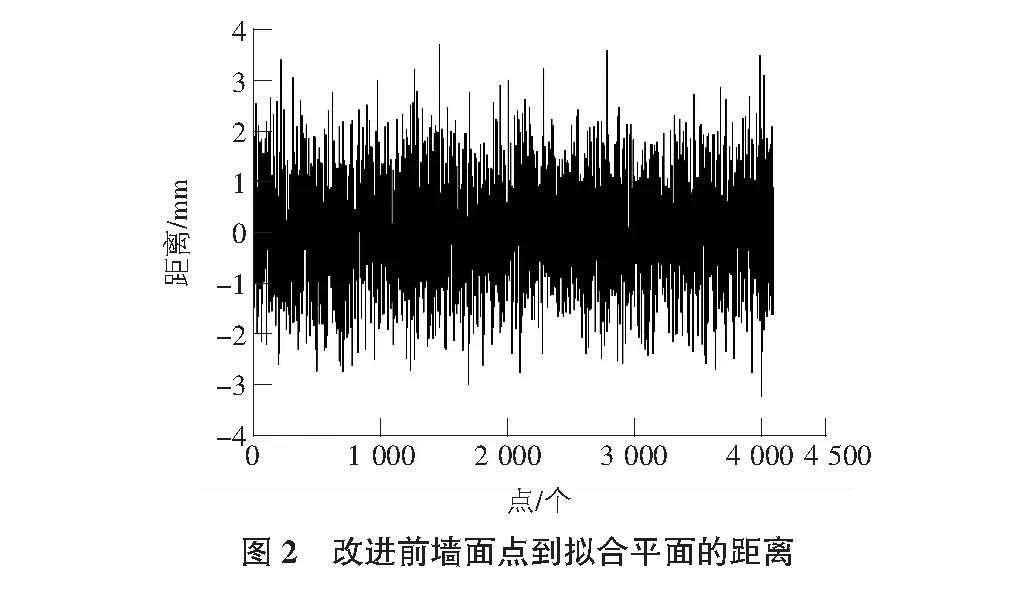
利用MATLAB软件处理后，数据显示，改进后点到拟合平面最大的距离是3.632 mm，最小的距离是-3.367 mm，整体分布情况大致符合正态分布。经计算得到优化权函数后墙面平整度为1.722 8，满足墙面平整度的精度要求，并且较改进前1.732 0有显著性提高，说明方法有效可行。

5 结语

通过以上实验及分析，利用三维激光扫描技术对房屋监测中墙面平整度的检测方法可靠精确，在Huber选权迭代法中引入RANSAC算法思想能够有效减小粗差的影响，提高墙体点云数据的精度，优化墙面拟合平面多项式，对于墙面平整度的计算有积极的作用。但在选权迭代算法中仍有很大的改进空间，例如选权迭代算法中c值的选取也会对墙面平整度的检测有很大的影响。