中法海洋卫星微波散射计风场反演残差特性研究

王冰花，董晓龙*，林文明，郎姝燕，朱迪，云日升

( 1. 中国科学院大学，北京 100049；2. 中国科学院国家空间科学中心 微波遥感技术重点实验室，北京 100190；3. 南京信息工程大学 海洋科学学院，江苏 南京 210044；4. 国家卫星海洋应用中心，北京 100081)

1 引言

海面风场是海洋和大气科学研究与应用中的重要物理参数。星载微波散射计作为当前获取全球海面风场信息最主要的遥感仪器，其观测结果在数值天气预报、海洋灾害监测、海洋环境数值预报、气象预报和气候研究等方面发挥了重要的作用[1-2]。

散射计观测风场质量对数值天气预报的精度有着重要影响。因此，在海面风场的诸多应用中，对风场质量的定量化描述尤为重要，通常用风场质量敏感因子来实现，其中最常用的一种质量敏感因子是风场反演代价函数的残差[3]。卫星散射计海面风场反演最常用的算法是最大似然估计法（Maximum Likelihood Estimation, MLE），风场反演的残差也称作MLE值，表示一组测量的后向散射系数（ σ0）与地球物理模型函数（Geophysical Model Function, GMF）构成多维参考面之间的距离[4]。通常情况下，散射计测量的海面 σ0与GMF模拟的 σ0最为接近，反演的风场质量高、MLE值小。然而，当风单元（Wind Vector Cell, WVC）中的雷达后向散射信号主要受到除风以外的其他地球物理条件的影响时，实际测量的 σ0和GMF仿真得到的σ0值会有较大的差异，导致MLE值偏大[5]，由此可见，MLE是一个很好的风场质量指示标志。另一方面，在风场去模糊处理过程中，MLE值越大，相应的模糊解被选中为“真实解”的可能性的就越小，反之亦然。因此，MLE值还包含模糊解为真实解的概率，广泛用于数据同化和二维变分分析模糊去除（2D_Var）[6]。

图1为中法海洋卫星散射计(CSCAT)风场反演流程图，图1中输入的L1B级数据包括条带后向散射系数及其辅助数据，其中条带后向散射系数要经过面元匹配、外定标等过程变换成网格后向散射系数才能进行风场反演。面元匹配是将按时序存储的后向散射数据以及后向散射系数对应的观测几何信息等参数，重采样到风矢量单元。外定标的目的是校正内定标环路之外的仪器不确定因素引起的后向散射系数偏差，对每个独立的测量都要进行外定标，外定标的精度会影响残差的数值结果，外定标精度越低，风单元多次观测之间的不一致性越大，残差值就越大，风场反演的质量越低。通过面元匹配和外定标处理生成的L2A级网格后向散射系数，为后续风矢量反演提供输入参数。

图1 CSCAT风场反演流程图Fig. 1 Wind retrieval flow chart of CSCAT

L2A级后向散射系数通过最大似然估计得到风场模糊解。风场模糊解在模糊去除之前需通过模糊解似然概率模型函数将反演的MLE值转换为真实解的概率。概率模型函数的参数与MLE值特性有关，目前CSCAT标准的风场反演流程采用的是笔形波束旋转扫描散射计的经验概率模型函数。由于CSCAT散射计采用了新的观测几何（图2），这种观测几何大大增加了对风单元的观测次数。以往的散射计对同一海面风矢量单元的观测次数一般为2～4次，CSCAT对刈幅内每一个风单元的观测次数高达4～16次，每个观测视数包含25～50个观测条带后向散射信息，提供了远比其他微波散射计更多的后向散射信息。由于CSCAT的观测几何与以往散射计的都不相同，其反演残差特性也会有所不同，因此本文对CSCAT反演残差特性进行了详细的研究并建立了与风单元位置相关的似然概率模型函数。

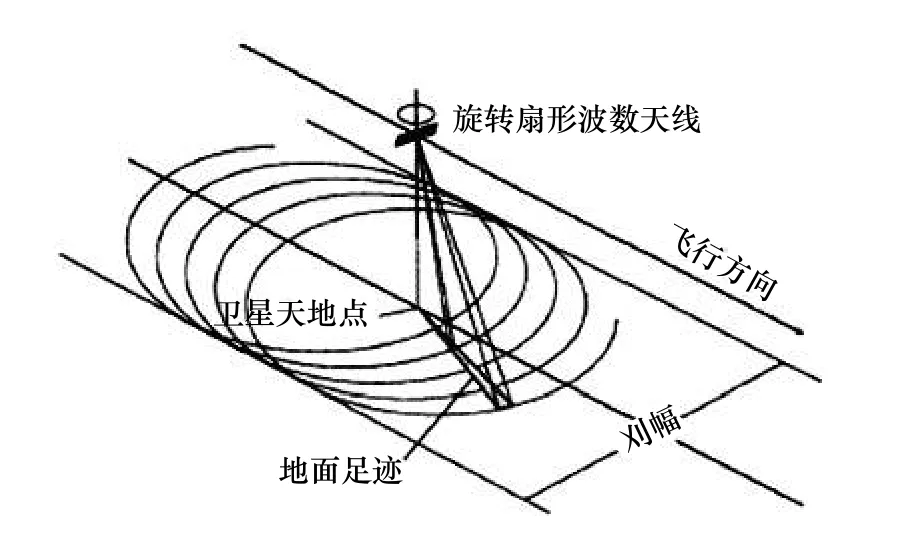
图2 CSCAT观测几何示意图Fig. 2 Schematic diagram of observation geometry of CSCAT

CSCAT在数据处理中采用二维变分分析法进行模糊解去除[7]，二维变分分析是将数据同化到数值天气预报（Numerical Weather Prediction, NWP）模型中常用的方法[6]。由于降雨、海冰、未知海况等会影响后向散射系数从而降低风场反演质量[8-9]，所以要对模糊去除之后的风场进行质量控制以检测和剔除不合格的风矢量单元，最终获得L2B级风场产品。

本文基于最大似然估计风场反演算法，研究CSCAT观测几何下风场反演代价函数的残差特性。

2 数据与模型

2.1 数据

CSCAT是国际上第一个在轨运行的扇形波束旋转扫描微波散射计，与固定扇形波束和旋转笔形波束散射计相比，CSCAT可以进行大入射角范围、多方位向、覆盖范围广的后向散射系数观测[10]。这种新的观测机制为海面风场反演提供了比以往散射计更多的观测信息，在提高风场反演质量的同时，也给风场反演代价函数的构建和求解带来新的挑战。Liu等[7]研究发现，CSCAT在2019年期间的数据都比较稳定，所以我们采用CSCAT 2019年3月和5月3.0版本L2B级风场数据研究CSCAT风场反演代价函数的残差特性。

CSCAT的刈幅在沿轨方向划分成一系列行，每一行包括42个分辨率为25 km的风单元，风单元编号从最左端开始向最右端（以卫星前进方向为参考）依次递增，如图3所示。其中，1～5列和38～42列为刈幅远端，6～17列和26～37列为刈幅中间部分，18～25列为星下点区域。

图3 CSCAT地面风单元划分Fig. 3 CSCAT ground wind vector cell meshing

风场数据的辅助数据主要有海冰、海陆及欧洲中期天气预报中心（European Centre for Medium Range Weather Forecasts，ECMWF）数据。海陆、海冰数据用于地面类型识别，以海陆分布图和海冰分布图作为基本判断标准，结合每个风矢量单位（Wind Vector Cell,WVC）中心的地理位置，对WVC所对应的地面类型进行判断。其中，海陆分布图使用的是ECMWF提供的高分辨率海陆掩膜。海冰掩膜是由欧洲气象卫星组织海洋海冰应用中心提供的每日南北半球的海冰边缘线融合产品。参考风场采用了相应时间范围的ECMWF预报风场，ECMWF每天在0点和12点发布预报风场，预报风场时间间隔为3 h，空间网格分辨率为0.125°，通过空间双线性插值和时间样条插值获取散射计观测位置和时间的匹配风场，进行时间插值时应有两个背景风场数据在散射计测量时间点之前，一个背景风场数据在散射计测量点之后。考虑到ECMWF预报数据获取的时效性，本研究使用的预报时间在3～18 h之间。

2.2 CSCAT风场反演模型

随着散射计技术的不断发展和完善，形成了多种风场反演方法，其中最常用的是最大似然估计[11]，CSCAT最大似然估计的代价函数定义为[12]

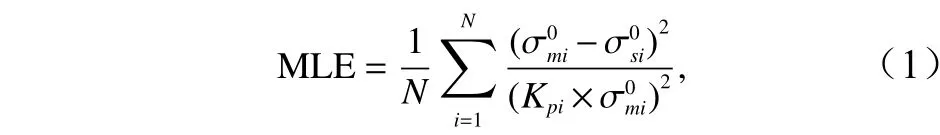
式中，N是独立观测的次数；i是独立观测的序号；和分 别表示第i个视图观测的后向散射系数和仿真的后向散射系数；Kpi是后向散射测量的归一化标准差，可以根据下式进行估计[13]：

式中，M(通常为20～30)是分到第i个视图的条带总数；是第j个条带的后向散射值。

每个风矢量单元在反演时都可以得到一个代价函数，MLE代价函数曲线的形状很大程度上决定了反演风矢量的准确性，图4为CSCAT第39列某一风单元的MLE代价函数与风向风速曲线关系的示例。MLE与风向曲线关系中存在4个极小值点，由此可以确定，在MLE反演过程检索到对应的4个模糊解，代价函数曲线取得极小值时附近的曲线形状和模糊解的真实性有关。第1个与第3个极小值附近的曲线比较宽，这时反演得到的风矢量偏差较大。因为此时极小值附近的风矢量是真实风矢量的概率和极小值对应的概率相当，但是这些概率相当的MLE中只有一个被选中。

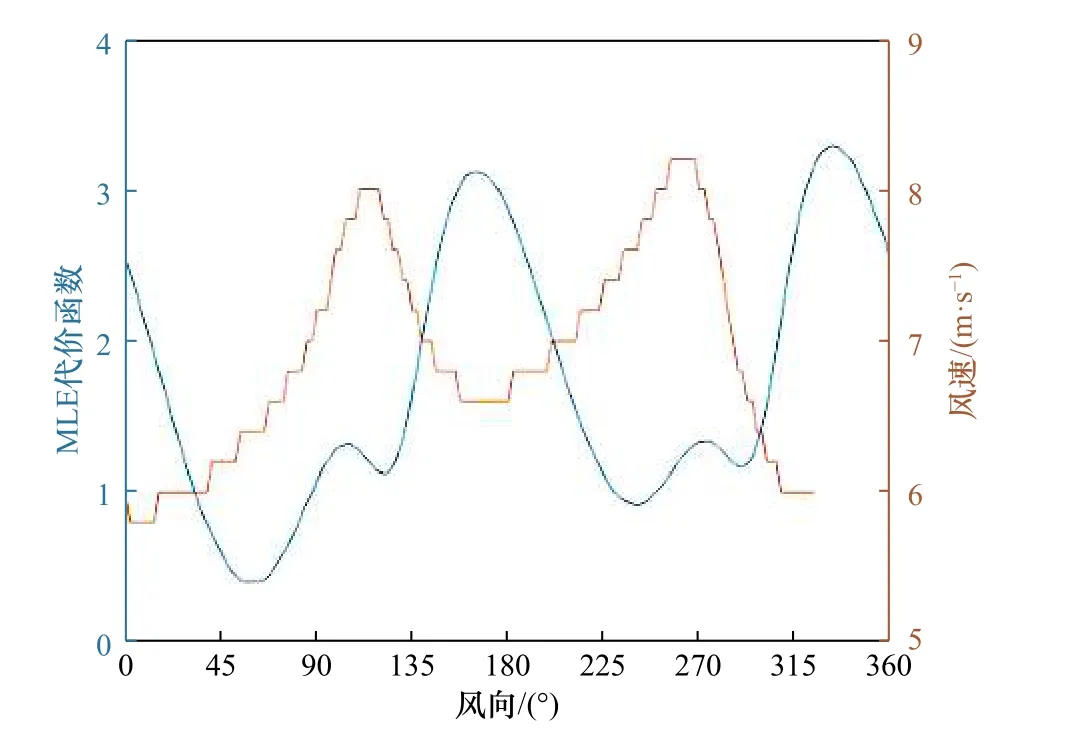
图4 MLE风场反演曲线Fig. 4 Curve of MLE wind inversion

为了避免代价函数曲线极小值点较宽导致的风场反演偏差较大的情况，CSCAT结合多解方案(Multiple Solution Scheme, MSS)[14]进行风场反演，MSS反演中通常将风向从0°到360°每隔2.5°进行划分，对于每个风向，通过对代价函数求极小值计算得到与之相对应的风矢量。每一个风单元可以得到144个风矢量解，其中只有一个是真实解，其余的称为模糊解。为了得到真实解还要进行风向的模糊去除。

3 残差特性分析

3.1 CSCAT的残差分布特性

为了分析CSCAT的MLE残差分布特性，本文研究了MLE平均值及标准差随风速和WVC列数的变化，并根据卫星数据产品的质量标识符，剔除了陆地、海冰区域以及其他质量不合格的风矢量单元数据。然后计算相同节点相同风速下所有被选中MLE值的平均值和标准差（图5），通过风场反演会得到4个模糊风矢量及其对应的MLE值，通过模糊去除选择真实风矢量的模糊解对应的MLE值，即被选中的MLE值。从图中可以明显看出MLE的分布与风速有很强的相关性。随着风速的减小，MLE均值和标准差均呈上升趋势；由于CSCAT的观测几何随着节点数变化较快，不同列的风单元之间也存在明显差异，在刈幅远端的风速偏差和标准差都较大，因为刈幅远端为大入射角观测，σ0的精度降低[7]，导致观测的 σ0和GMF得到的仿真值差别较大。星下点区域在中等风速时偏差和标准差明显增大是因为该区域观测入射角信息丰富，观测方位角集中在180°左右，由于非风场因素的地球物理噪声的影响及质量控制的效果在中等风速出现的概率最大，质量控制虽然能剔除一部分海冰、降雨等因素引起的质量较差的观测，但无法完全识别和剔除，所以在中等风速时偏差和标准差明显增大。

图5 平均MLE随风速和WVC列数的变化（a）及MLE标准差随风速和WVC列数的变化（b）Fig. 5 Mean MLE versus wind speed and WVC number (a) and MLE standard deriation versus wind speed and WVC number (b)

图6、图7是同一时间内不同节点下CSCAT风速、风向相对于ECMWF风速、风向的偏差和标准差随平均MLE变化的曲线。对比偏差和标准差可以明显看出不同节点的风速、风向偏差存在明显差异，MLE值较大时，不同节点的风速差异可达到0.2 m/s。风速、风向的标准差随MLE的增大呈上升趋势，不同节点之间略有不同，所以要区分不同的节点研究反演的残差特性。

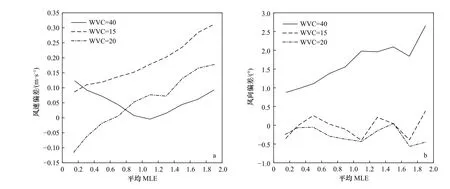
图6 CSCAT风速、风向相对于ECMWF风速、风向的偏差随平均MLE变化的曲线Fig. 6 The variation curve of CSCAT wind speed and direction bias relative to ECMWF wind speed and direction with mean MLEa. 风速偏差；b. 风向偏差；不同线型的曲线表示不同的WVC列数a. Biases of wind speed; b. biases of wind direction; lines in different styles are for different WVC number

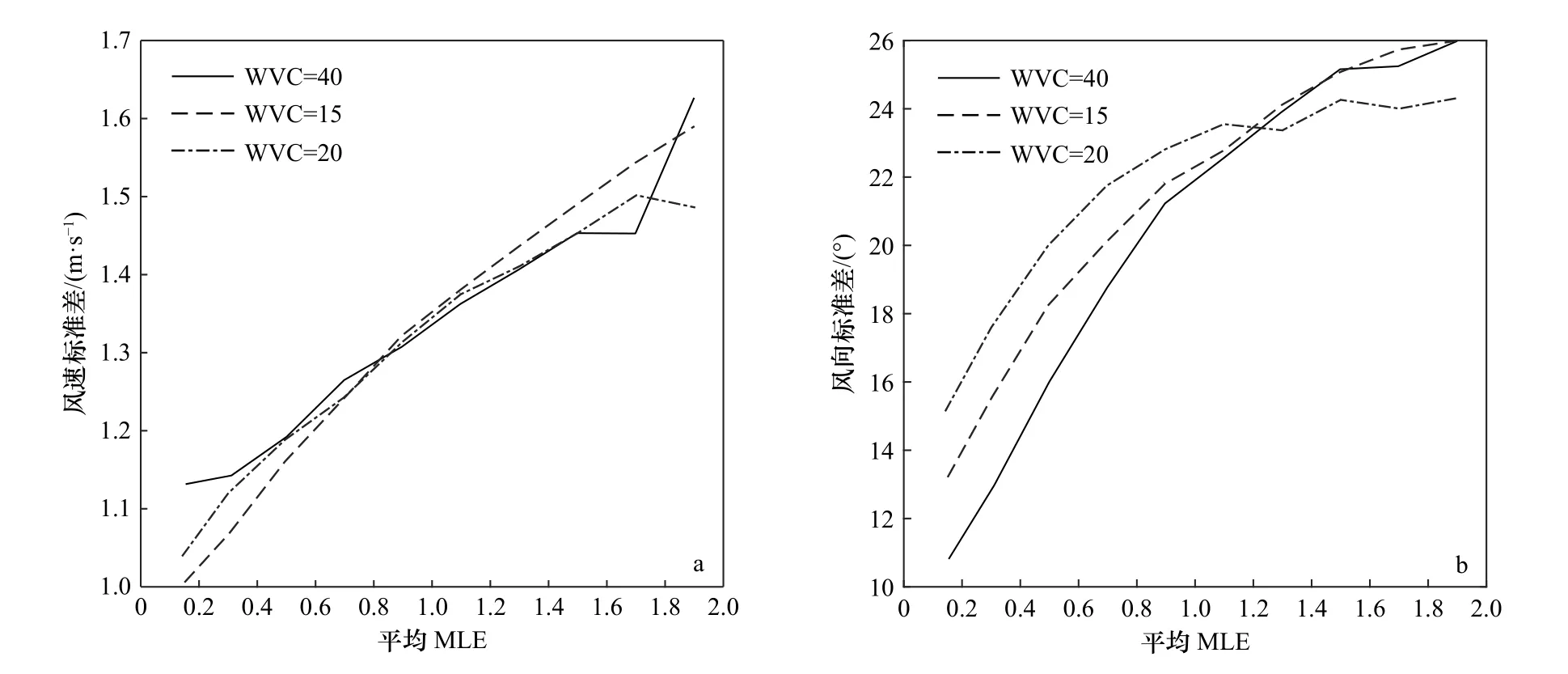
图7 CSCAT风速、风向相对于ECMWF风速、风向的标准差随平均MLE变化的曲线Fig. 7 The variation curve of CSCAT wind speed and direction standard deviation relative to ECMWF wind speed and direction with mean MLEa. 风速标准差；b. 风向标准差；不同线型的曲线表示不同的WVC列数a. Standard deviation of wind speed differences; b. standard deviation of wind direction differences; lines in different styles are for different WVC number

3.2 似然概率模型函数

反演得到的模糊解要通过模糊去除选择一个模糊解作为真实解，模糊解被选为真实解的概率即模糊解似然概率，根据贝叶斯理论[15]和公式（1），散射计反演的模糊风矢量是真实风矢量的概率可以表示为与MLE有关的函数：

式中，v表示“真实”风速； σ0表示一系列散射计后向散射系数测量值；k是标准化比例因子。因此，该概率函数理论上是一个和MLE相关的指数函数关系。从上式可以看出MLE值越小，模糊解成为真实解的概率越大。模糊风矢量越接近真实风矢量，MLE值越小，由公式(3)得到的概率值就越大。概率值较大的模糊风矢量也越接近真实风矢量，因此概率函数模型与MLE值的含义是一致的。在实际应用中，由于存在一些观测误差，指数函数的形状可能与理论值不同。

Portabella和Stoffelen[16]首先提出在QuickSCAT质量控制中采用归一化的MLE值或归一化的残差替代MLE，目的是解决MLE反演方法过程中存在的问题和噪声估计，Portabella和Stoffelen[16]通过统计分析得出QuikSCAT的概率模型函数表达式为

式中，x代表归一化残差。

本研究中，设CSCAT的概率模型函数表达式为

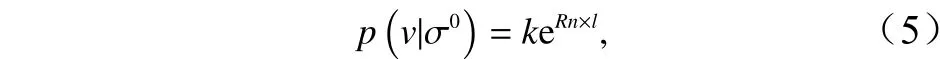
式中，k为归一化因子；l为要根据经验推导的参数；Rn是归一化的残差。为了获得经验公式(5)的具体形式，可以忽略先验知识对指数关系的影响，并假设存在一个函数关系ps(x)，对于某一风矢量单元，如果有N个模糊风矢量vi和相应的归一化最大似然值Rnj，则其中第j个风矢量最接近真实风矢量的概率可以表示为

为了得到ps(x)函数的具体形式，本文对CSCAT L2B级数据进行了分析，研究只有两个模糊解的风矢量单元。选择与ECMWF风场最接近的模糊解作为选择解。统计每一阶的模糊解作为选择解的个数，可以得到每阶模糊解为真实风解的概率。在公式中令N为2，可以的到第一阶模糊解成为真实解的概率是：

通过公式(7)的运算可以得到每阶统计概率，进而得到ps(Rn2)/ps(Rn1) 的估计值。图8是Rn1为0.1时概率函数曲线随节点位置的变化情况，可以看出星下点下降速率最慢，刈幅远端下降速率最快，表明随着MLE的增大，模糊解成为真实解的概率急剧减小，说明较小的MLE值对应的解成为真实解的概率更大，有更多的风单元选择一阶模糊解作为真实风矢量解。

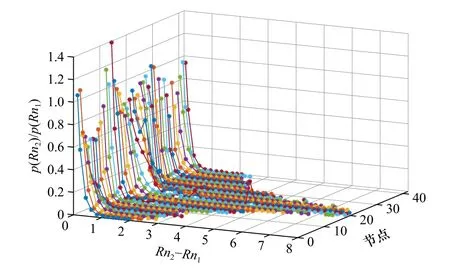
图8 不同节点下（ Rn2−Rn1 ） 值与 p(Rn2)/p(Rn1) 函数关系的指数拟合（ R n1=0.1）Fig. 8 The exponential fit to ratio R n2 and R n1 as a founction of (R n2−Rn1) value for different WVC number（ Rn1=0.1）

图9为通过实验数据确定的第8列所有风单元的Rn1和Rn2组合的比率函数关系。尽管曲线较为离散，但是总体明确表明当Rn1小 于2时，P(Rn2)/P(Rn1)比值是关于Rn1和Rn2不变的指数关系函数，符合公式(5)假设的曲线关系。当Rn1是 一个常数时，ps(Rn1)也是常数，图9表现了ps(x)的曲线形状。

从图9中可以看出，指数函数的下降速率与Rn1的取值有关，当Rn1较大时不再符合指数关系，为了找出原因对Rn1的 分布特性进行了统计（图10），从Rn1分布直方图可以看出Rn1的绝大多数值分布集中在0～1之间，Rn1较 大时，由于在此范围的风单元数量很少，ps(x)不 符合指数函数关系。

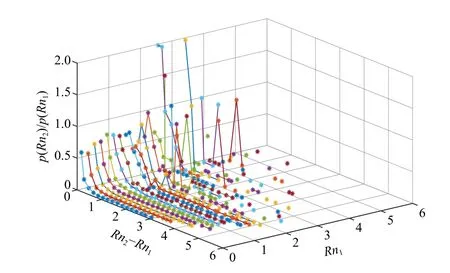
图9 不同 R n1取 值下 p(Rn2)/p(Rn1)与 （ R n2−Rn1）值函数关系的指数拟合（第8列WVC）Fig. 9 The exponential fit to ratio of R n2 and R n1 as a founction of (R n2−Rn1 ) value for different R n1 (WVC number 8)

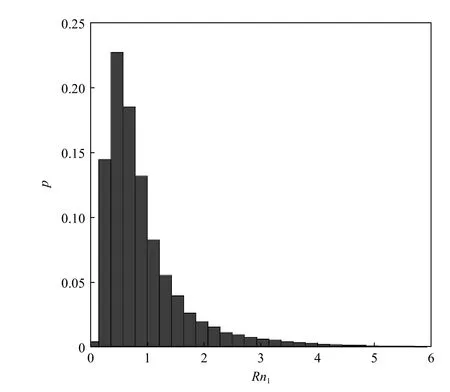
图10 R n1分布直方图（节点数为8）Fig. 10 The distribution histogram of R n1 (the number of node is 8)

3.3 结果与检验

通过以上分析可知，概率函数的指数是与风单元列数有关的，由于不同位置的风单元观测数量不一样，MLE代价函数的维度也不一样，所以不同位置的风单元概率函数的指数也不一样。根据刈幅不同区域位置和Rn值的不同分布情况，可以得到每一列指数拟合的系数和指数，结果如图11所示。刈幅不同区域的概率函数差别较大，整体呈现一定的对称性，指数l分布在−0.4～−1.8，与笔形波束散射计的指数不同，概率函数的系数分布在1左右。

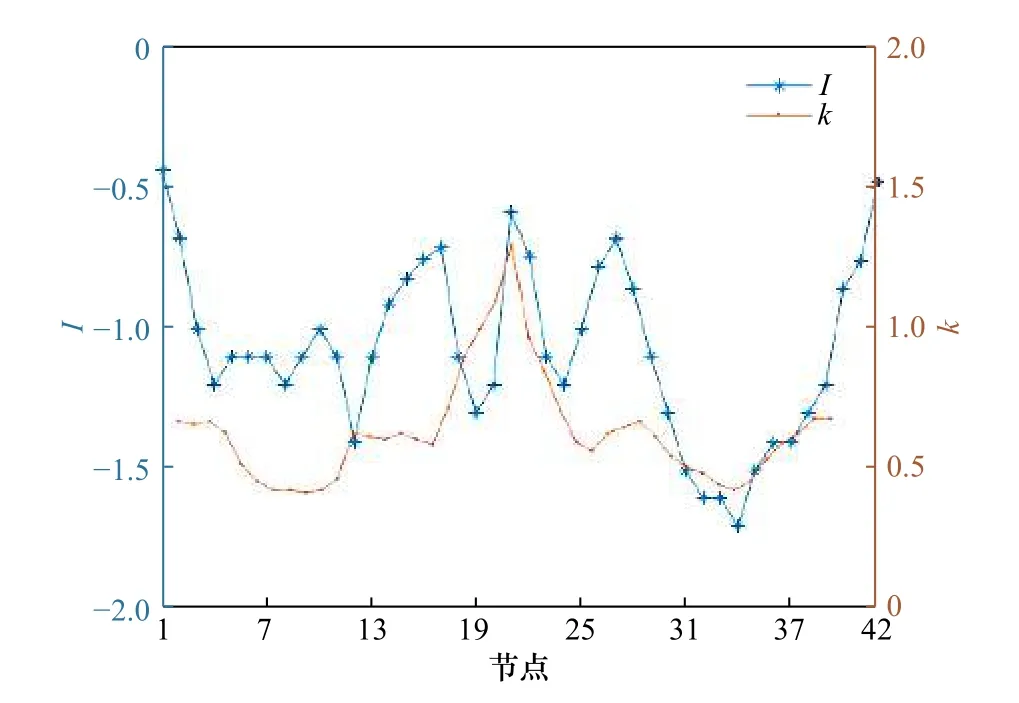
图11 概率模型函数的指数及系数随节点的变化Fig. 11 The exponents and coefficients of the probabilistic model versus node number

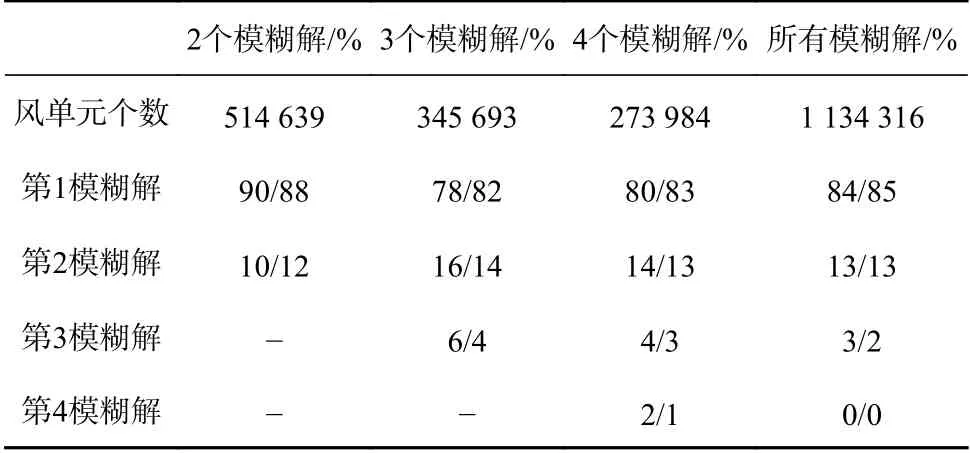
表2 预测概率/观测概率的分布对比(刈幅中间)Table 2 Distribution comparision of predicted probability/observed probability (sweet swath)

为了验证之前的假设是否正确，能否推广到有多个解的情况，本文对2019年5月份的150轨CSCAT散射计L2B级数据进行了分析，并推广到有多个解的情况，统计每一级模糊解成为真解的预测概率。表1至表3分别对不同区域每一级模糊解的预测概率和观测概率进行的对比。表中第一行表示在所有研究数据中风矢量单元模糊解个数为2、3、4的风矢量单元的总数。第2行至第5行中左侧数据表示每一阶的所有模糊解概率值的平均值，即预测概率，右侧数据表示统计每一阶模糊解是真解(最接近ECMWF风场)的个数占所有模糊解个数的百分比，即实际观测概率。通过对比每一列的预测概率和观测概率可以看出明显的相关性，刈幅远端和中间区域存在微小差别，这是因为前文拟合曲线时，曲线本身是有波动的，但是总体对比表明一致性很显著。星下点差别较大，这是因为星下点进行拟合时不是标准的指数关系。因此，可以证明之前的假设是正确的，拟合的与风单元位置相关的概率模型函数可以用来计算某一模糊解为真实风矢量的概率。

表1 预测概率/观测概率的分布对比(刈幅远端)Table 1 Distribution comparision of predicted probability/observed probability (far swath)

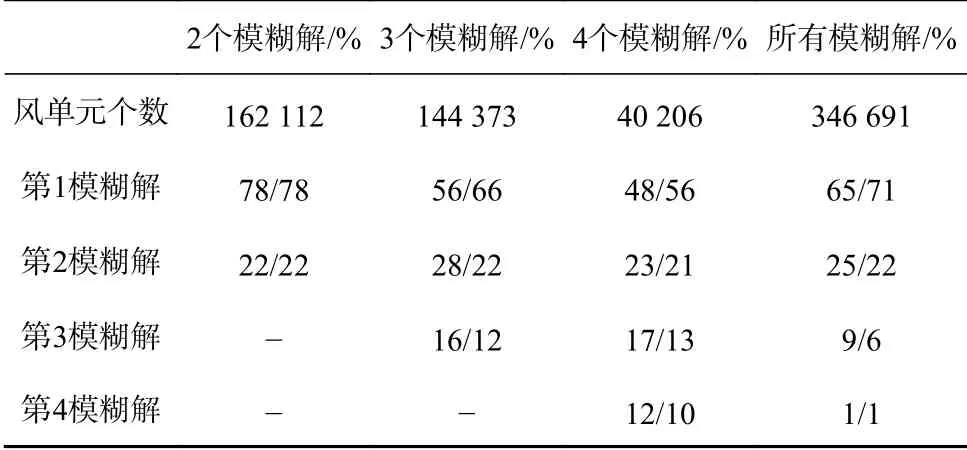
表3 预测概率/观测概率的分布对比 (星下点区域)Table 3 Distribution comparision of predicted probability/observed probability (nadir swath)

为了检验上文拟合得到的似然概率模型函数反演风场的效果，分别采用与风单元位置相关的概率模型函数与标准反演过程中的概率模型函数进行风场反演，得到相应的风产品，并收集美国浮标数据中心的浮标数据与反演风场进行对比。图12和图13是两种方法反演的风场与浮标风场的散点图对比结果。可以看出采用与列数相关的概率模型函数反演的风场偏差减小了0.03 m/s，而标准差未发生变化，表明风速的离散度未发生变化，而风速的准确性有提高。对比风向变化可以发现风向偏差未发生变化但风向偏差减小了0.2°，风向标准差减小了0.5°，表明改进的概率模型函数反演的风场精度有明显的提高。

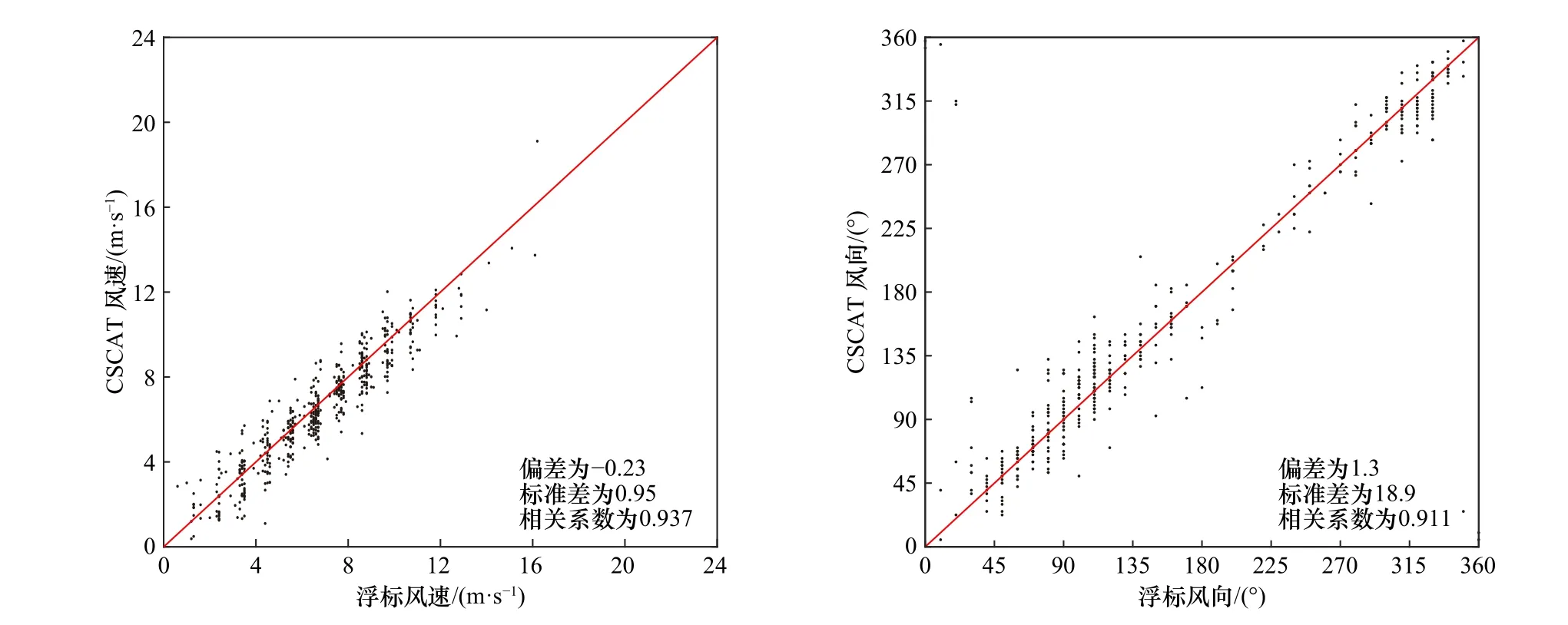
图12 改进前概率模型函数反演的CSCAT风场与浮标测量风场Fig. 12 CSCAT wind filed and buoy wind filed retrieved by the likelihood probability model before improvement

图13 改进的概率模型函数反演的CSCAT风场与浮标测量风场Fig. 13 CSCAT wind filed and buoy wind filed retrieved by the improved likelihood probability model

4 总结与展望

本文基于最大似然估计风场反演算法，探讨了CSCAT新的观测体制下反演残差分布特性。在理论推导的基础上，利用CSCAT观测数据，定量拟合了似然概率模型函数与WVC列数的关系。

CSCAT反演残差与风速和WVC列数有关，MLE平均值、标准差随风速和列数有较为明显的变化，反映了CSCAT数据用于风场反演时自身的一些特点。不同WVC列数的CSCAT风速风向与ECMWF风速风向差别较大，并且风速风向标准差变化趋势比较一致，偏差变化明显不同。

在风场反演时，MLE代价函数被转化成似然概率代价函数用于风场的模糊去除，在第3节本文研究了模糊解是真实解的概率问题，并根据不同区域的残差对所有节点进行指数拟合，发现不同区域的概率模型函数参数有明显的差别。为了对本文拟合结果进行验证，本文利用2019年5月份的数据对实际观测概率与通过本文的概率模型函数得到的预测概率进行对比。结果表明，本文提出的概率模型函数能够有效预测模糊解成为真实解的概率。最后对改进的概率模型函数反演的风场进行检验，可以发现风场反演的质量有明显的改进。

分析结果为后续CSCAT风场质量控制和2D_Var算法的精细化调整提供了重要的参考。CFOSAT从2018年发射以来，已经获取了大量宝贵的海面风场观测数据，随着数据的积累和算法的改进，CFOSAT微波散射计必将为海洋观测和应用做出更大的贡献。