不同补沙方案对海滩剖面影响的数值模拟对比分析

梁丙臣，朱梅溪，屈智鹏*，王聪，李东永,3

( 1. 中国海洋大学 工程学院，山东 青岛 266100；2. 海南省环境科学研究院，海南 海口 571126；3. 韩国海洋科学技术研究院，韩国 釜山 49111)

1 引言

沿海地区被认为是世界上人口最稠密、发达程度最高的区域之一，而这些地区取得的发展对海岸带资源有着极大的依赖性。其中砂质海滩蕴含着丰富的资源，对于人类社会具有至关重要的经济功能和生态功能，同时，对于沿海地区也具有一定的防护作用。在风、潮汐、洋流和波浪等作用下，海滩处于不断变化的状态，而砂质海滩由于其自身的组成成分及地理位置特点，对外部环境变化有着高度敏感性[1]。由于气候变化以及人类在海岸带的建设活动等因素，砂质海岸的侵蚀后退愈发严重。1984−2016年，世界上24%的沙滩正在以超过0.5 m/a的速率受到侵蚀[2]；到21世纪末，35.7%～49.5%的沙滩将面临严重的侵蚀问题[3]。许多学者提出，人工补沙是当前解决海岸侵蚀最自然有效的办法[4-5]。人工补沙又称“海滩养护”，通过规划设计向海滩抛置大量泥沙，以达到扩宽和稳定沙滩的目的[6]。这种方法在有效缓解侵蚀状况的同时，对生态环境的影响也大大降低[7]。美国早在1922年就提出了人工沙滩的概念并加以实践，采用人工填沙的方法造就新的沙滩，优点在于对上下游的影响较小，但投资较大，且需定期维护[8]。20世纪70年代以来，欧洲沿海各国普遍采用抛沙养滩为主、硬工程为辅的护岸措施，并广泛用于海岸防护工程[9]。随着生活水平的提高，人们对滨海旅游的需求日益提高，对优质海岸资源也就有了更高的要求。因此，我国近些年来人工补沙工程发展迅速，海滩养护的规模也在不断扩大。三亚三美湾沙滩的沉积物粒径较大，导致沙滩利用价值低，通过人工沙滩和修建潜堤改善了沙滩情况[10]；海南省桂林洋海滨旅游区海滩进行人工海滩补沙和离岸堤布置，改善沙子的质量、扩宽沙滩宽度[11]；厦门岛砂质海岸存在不同程度的侵蚀后退，沙滩形态遭到破坏，于是在原有沙滩的基础上通过填沙来修建人工沙滩[12]。

在人工沙滩建设及养护设计过程中，海滩平衡剖面理论是主要依据。海滩平衡剖面，是在一定条件下，海滩上任一点泥沙均没有净位移，剖面形状维持不变的海滩形态。在天然海滩上，动力条件变化复杂，海滩地形也在随时发生变化，海滩剖面形状的变化可以看作是随着动力条件的变化，从一种平衡状态到另一种平衡状态的调整[13]。由于海滩上动力因素和泥沙运动的复杂性，精确预测海滩平衡剖面难度大，因此目前提出的海滩平衡剖面公式多以半经验公式为主。Dean[14]通过分析美国大西洋海岸和墨西哥海岸的500多个实测海滩剖面形状提出了指数型海滩平衡剖面曲线（以下简称Dean曲线）。目前，Dean曲线是判定海滩剖面是否达到平衡的一种较为客观的判别依据[15]。本文通过对比海滩剖面模拟值与Dean曲线之间的差距来估计海滩是否到达平衡剖面。

我国的海滩养护研究起步较晚，但发展迅速，截至2019年，我国修复岸线总长度超过120 km，总投资超过2.0×109元[16]。而由于实际条件的限制，海滩养护后剖面在波浪作用下的演变难以观测，对于补沙后剖面上的泥沙重新分布过程的认识并不清晰。因此，需要大量的物理模型试验和数值模拟试验来研究补沙后沙滩剖面的演变情况，以此来评估工程的有效性。本文建立实验室尺度下XBeach一维海滩剖面演变数值模型（以下简称XBeach模型），并将该模型与物理模型实测数据进行对比验证；设计补沙方案进行数值模拟计算；比较在常浪下不同补沙位置、不同补沙量时海滩达到平衡剖面的速率，通过对比补沙工况与未补沙工况的风暴后剖面，分析风暴作用下的补沙效果。本文对不同补沙方案的时间效率和防护效果综合评价，从而为提高补沙效率、节约施工成本、维持沙滩养护工程稳定性等实际工程的技术提供参考。

2 模型验证

本文采用XBeach模型进行数值模拟分析。XBeach模型[17-18]是基于过程的二维平面海岸动力学数值模型，用于模拟潮波、海啸波、风暴潮以及相应的海岸线演变、海床演变和泥沙输运等海岸动力学过程。XBeach模型主要有3种模式[19]：（1）“Stationary”模式，这种模式可以高效地解决波浪平均方程，但是未考虑次重力波；（2）“Surf-beat”模式，以相位平均的方式处理短波运动，可以解决短波在波群尺度上的变化以及与之相关的次重力波运动；（3）“Non-hydrostatic”模式，又称相位解析模式或非静压模式，可以解析所有波浪运动，相比之下在非静压模式下需要模型具有更高分辨率和更小的时间步长。

XBeach模型通过规则波作用下人工沙滩稳定性试验数据进行验证。物理模型试验在中国海洋大学工程水动力实验室的窄断面水槽中进行。水槽长为30 m，宽为0.6 m，深为0.8 m，实际岸滩布置如图1所示。试验采用天然沙，密度为2650 kg/m3，天然沙的平均中值粒径为0.1877 mm，波浪条件为规则波。该试验并不针对某一具体地区或某一工程项目原型，而是根据剖面类型判别公式来给出试验和原型海岸之间的相关性。剖面形态通过灰点（PointGrey）高速相机进行侧向观测，并结合图像处理技术实现岸滩剖面实时动态提取。人工沙滩稳定性试验得到不同工况下岸线沙坝演变情况以及达到稳定时的平衡剖面（图1）。

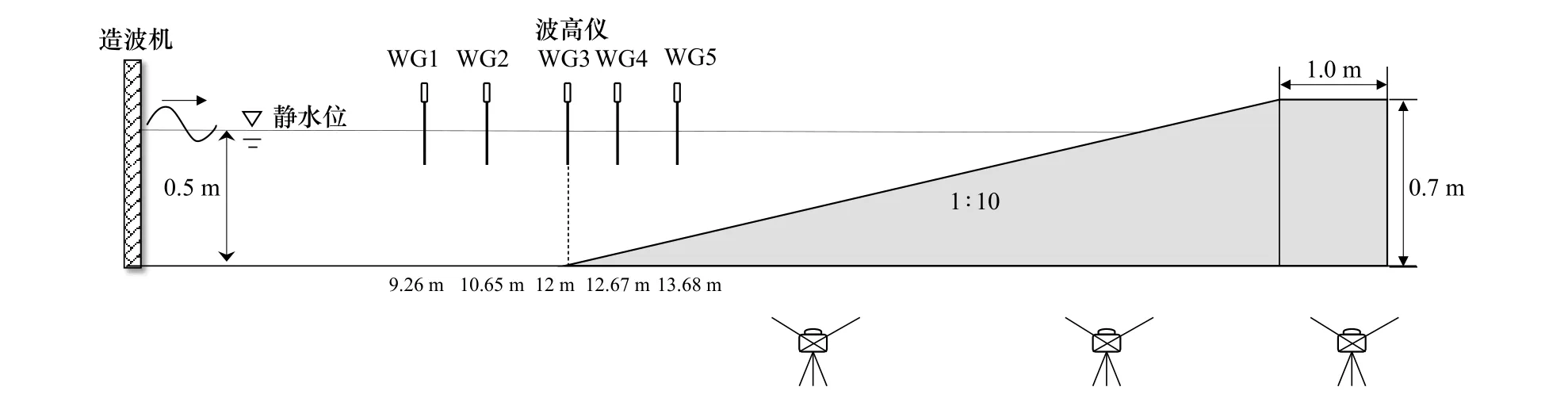
图1 人工沙滩稳定性试验布置示意图Fig. 1 Diagrammatic sketch of artificial beach stability test

由于试验尺度较小，经过模拟试验比较后，本文数值模拟选择在非静压模式下进行，可较好地模拟实验室尺度下的结果。模型范围为0～20 m，剖面位于12～20 m，采用均匀网格，网格数为300，网格大小为0.067 m×0.067 m。本次数值模型选取0.14 m、0.17 m两种波高，1.5 s、1.8 s两种周期进行验证，具体工况见表1。验证数据包括试验8 h后海滩剖面高程、波面时程数据以及沿程平均波高。

表1 人工沙滩稳定性试验验证工况Table 1 Validation cases of artificial beach stability test

波面时程变化如图2所示，选取距离造波机9.26 m和13.68 m处的两个波高仪实测数据进行验证；沿程平均波高验证结果如图3所示，其中蓝色标记点分别为5个波高仪的测量结果。通过观察图2和图3发现，实测数据和计算结果十分吻合，因此确定该数值模型可以用于模拟物理模型试验中的波浪条件。为判断模型对剖面高程模拟的准确性，将模拟8 h后的床面高程计算值与试验8 h后得到的测量值进行对比，结果如图4所示；同时，进行了相对于床面高程测量值的误差统计，计算结果如表2所示。其中，Brier技巧评分（Brier Skill Score, BSS）为经验系数，该参数将实测数据和模型结果之间差异的方差与数据的方差相关联。BSS等于1表示模型的模拟性能良好，BSS等于0表示拟合结果差，模型无法用于计算。决定系数R2，用来描述实测结果和模型结果之间的相关关系，评价拟合优度，R2越接近1，模型结果和实测数据的拟合程度就越大。分散指数（Scatter Index, SCI）则对误差进行规范化，避免了平均值小、变异性大的数据出现的异常结果，SCI值越小，模型性能越好。

图2 波面高程验证Fig. 2 Verification of wave surface elevation

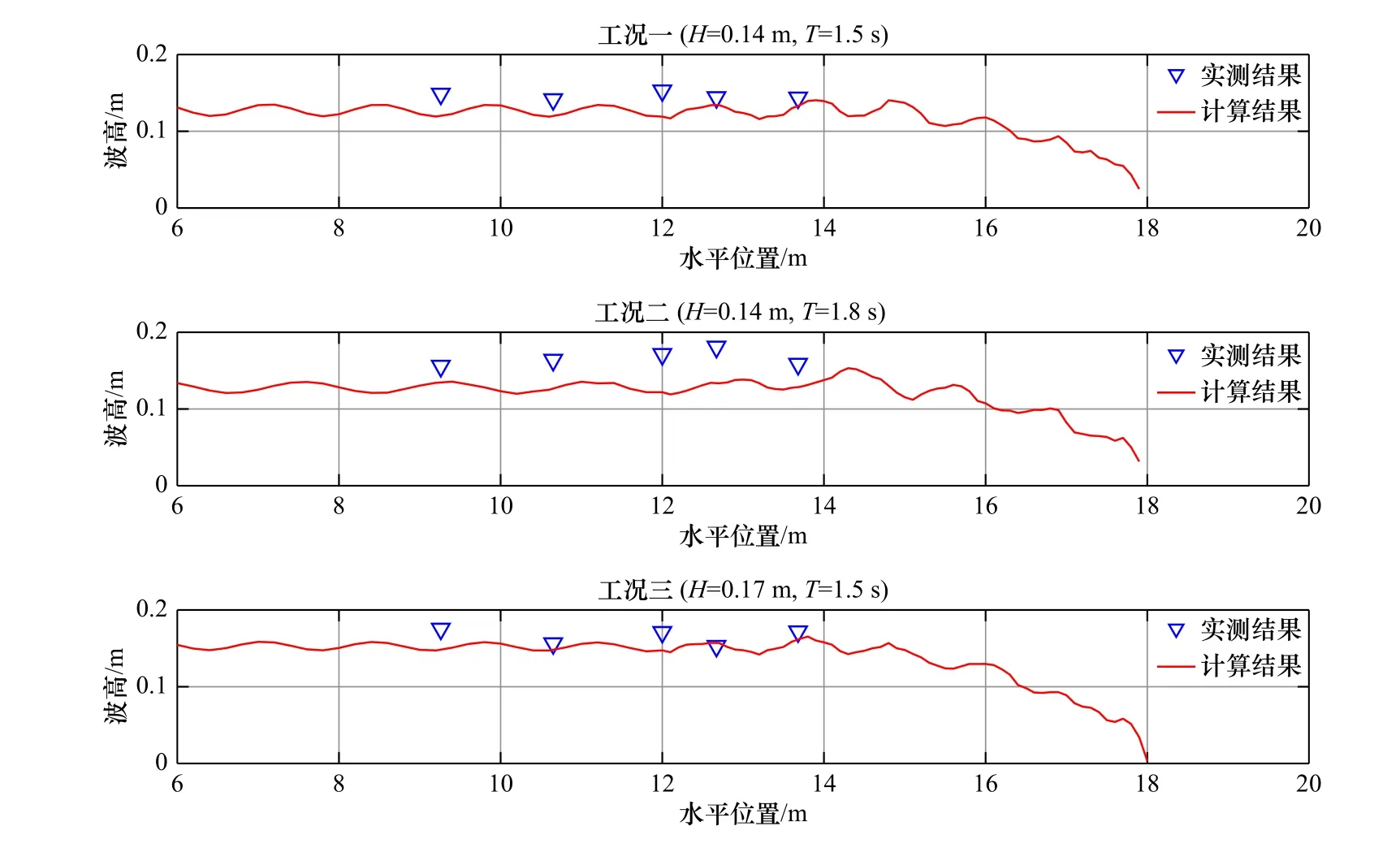
图3 沿程波高验证Fig. 3 Variation of wave height along the flume

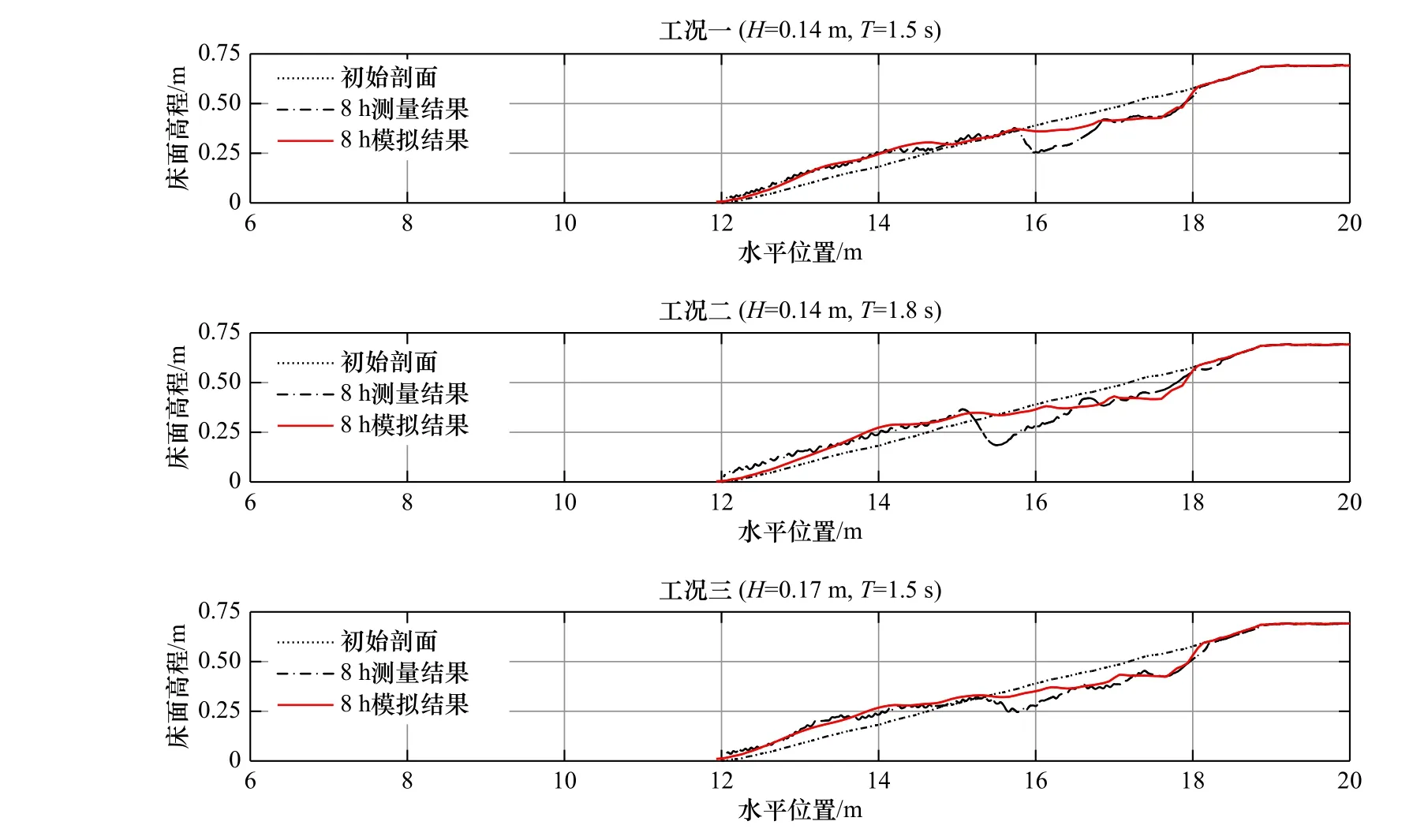
图4 床面高程验证Fig. 4 Verification of bed elevation

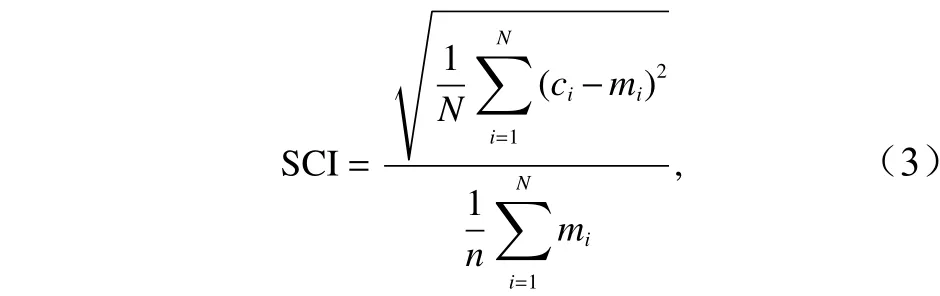
式中，m为测量值；c为模型计算值； σm为测量值的标准差； σc为模型计算值的标准差。

由表2中的误差分析结果可知，模型计算结果较好，可较为准确地模拟小尺度海滩剖面演变情况。通过图4可以看出，滩肩部分以及沙坝向海侧的剖面形态拟合较好，但计算得到的冲刷凹槽深度小于试验得到的结果，这与波浪在附近急剧破碎有关，在今后的研究中，将对模型采用的计算公式进行进一步的修正，并通过原型尺度下的物理模型试验进行进一步的探究。本文关注不同补沙方案恢复平衡剖面或者剖面达到平衡的速率，由误差分析可知，模型具有较高的可信度，能够用于整体沙量再分配时空演变模拟分析。

表2 数值模型误差统计Table 2 Error statistics of the numerical model

3 不同补沙方案的数值模拟

目前工程中使用的人工补沙位置主要分为4种：（1）沙丘补沙，将泥沙放置在平均高潮位以上，不增加干滩宽度，通过加固沙丘抵御风暴侵袭；（2）滩肩补沙，主要在平均水位以上填沙，可直接增加干滩宽度；（3）剖面补沙，将泥沙直接吹填在剖面上，短期效果明显；（4）近岸（沙坝）向海侧补沙，将补给泥沙抛置在近岸水下破碎区附近，能够起到削减波能和向岸供沙的作用[20]，是一种更为主动且环境友好的人工养滩方式[21]。相比较而言，滩肩补沙由于其施工难度较低，能够直接增加滩肩宽度且效果显著，是目前较常采用的海滩养护方案；而近岸（沙坝）补沙对环境影响较小，也是当前海滩养护研究中的重点问题之一。因此，本文选取滩肩和沙坝向海侧两处位置补沙进行常浪及风暴工况的数值模拟试验，探究两种位置的补沙效率、防护效果以及补沙量对养护后海滩剖面的影响。本次数值模拟试验所需常浪条件以及风暴条件根据剖面型式转变判数计算得到。Sunamura和Horikawa[22]基于水槽试验结果，根据泥沙运动方向将初始坡度均匀的海滩剖面分成3种类型。第I类：泥沙离岸方向运动，岸线后退，泥沙在离岸区堆积，属于侵蚀型海滩剖面；第II类：泥沙从破波点存在向岸和离岸两个方向的运动，滩面侵蚀下凹，岸线堆积同时形成沙坝，属于过渡类型；第III类：泥沙向岸方向运动，岸线前进，离岸区无泥沙堆积而有冲刷，属于堆积型海滩剖面，划分岸滩剖面类型的公式分别为

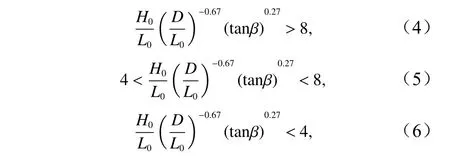
式中，H0/L0为深水波陡；D为泥沙粒径；L0为深水波长；tanβ为海滩初始坡度。

建立XBeach模型，该模型与验证模型对应相同尺度下的海滩剖面，且模型参数设置与第2节相同。根据海滩剖面判数计算结果，采用平均波高为0.08 m，周期为2 s的规则波作为常浪条件；将有效波高为0.15 m，周期为1.5 s的不规则波作为为风暴条件。

将1∶10均匀斜坡在风暴条件作用30 min后形成的风暴剖面作为补沙工况初始剖面，并进行后续补沙方案。模拟试验选择3种补沙量分别为0.1 m3/m、0.2 m3/m、0.3 m3/m，分别补在滩肩位置和沙坝向海侧位置，探究在常浪下两种补沙位置在不同补沙量下的补沙效率以及风暴下两种补沙位置不同补沙量的防护效果。补沙工况模型设置的初始剖面见图5，试验工况见表3。

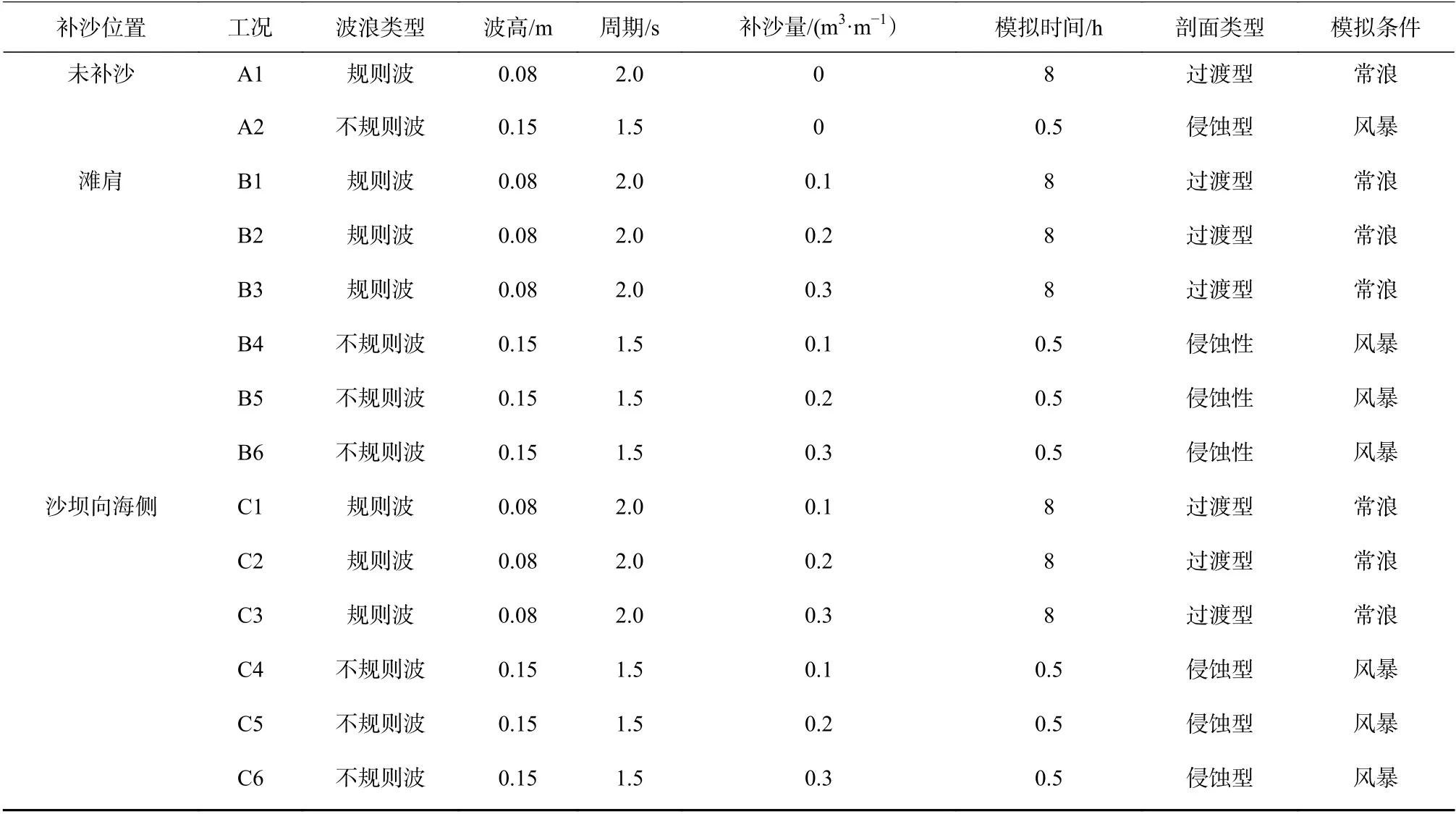
表3 数值模拟工况Table 3 Numerical simulation cases

图5 补沙工况初始地形Fig. 5 Initial terrain of nourishment casesa. 滩肩补沙；b. 沙坝向海侧补沙a. Berm nourishment; b. bar nourishment to the seaward

4 模拟结果分析

由于Dean模型能够反映海滩平衡剖面形态的平均形式，因此本文选择以Dean平衡剖面作为常浪工况下不同补沙方案海滩剖面到达平衡的参考剖面。本文采用RMSE值代表剖面高程模拟值与Dean曲线计算值之间的差异，通过RMSE值的变化反映人工补沙后在常浪条件下海滩到达平衡状态的快慢。将床面高程模型计算值与该海滩的平衡剖面曲线进行比较（图6），计算每个时刻补沙工况的海滩剖面高程模拟值与对应的Dean曲线之间的RMSE值，分析在不同补沙位置、不同补沙量时海滩趋向平衡剖面的速率。图7a、图7b分别对应滩肩补沙和沙坝向海侧位置补沙方案下不同补沙量工况之间的对比，并在表4中给出各补沙工况每小时的RMSE值变化率的计算结果。

图6 XBeach模型模拟8 h后对应的Dean曲线计算值（以补沙量0.3 m3/m为例）Fig. 6 The dean curve and XBeach model simulation after 8 hours (taking 0.3 m3/m sediment volume as an example)a. 滩肩补沙；b. 沙坝向海侧补沙a. Berm nourishment; b. bar nourishment to the seaward

式中，y为海滩剖面高程模拟值；h为Dean曲线计算值。

通过图7和表4可以看出，随着时间的推移，RMSE值的下降速率逐渐减小并接近零，说明海滩剖面趋近于Dean曲线的过程由快变缓并逐渐稳定下来，海滩剖面最终将到达平衡状态。通过对比图7a和图7b中补沙量相同时不同位置的RMSE值变化曲线可以看出，当补沙量较小（0.1 m3/m）时，滩肩补沙相对于沙坝向海侧补沙可以使海滩较快地到达平衡剖面。这是由于滩肩补沙体一部分位于水位变动区，波浪作用剧烈，直接将补充泥沙向海搬运与堆积，海滩快速趋向平衡。由图7a和图7b可以看出，随着补沙量的增多，滩肩补沙和沙坝向海侧补沙工况海滩趋向平衡剖面的速率均有加快，尤其是沙坝向海侧补沙时海滩趋向平衡剖面的速率明显增大，并超过滩肩补沙工况。这是因为在沙坝向海侧补沙时，补沙体充当了水下沙坝的作用，在消波减能的同时，全部补给量又作为沙源向海滩持续补沙。而滩肩补沙的大部分补沙体用于直接扩宽或加高干滩，在此常浪条件下，无法直接快速地作为沙源进入水下部分，因此增加平均水位上方的补沙量对加快海滩平衡过程作用不大，而增加沙坝向海侧补沙量，有利于加快平衡过程。

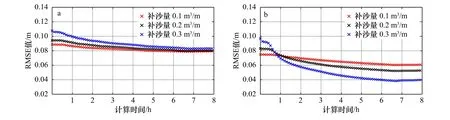
图7 剖面计算值与对应的Dean曲线之间的RMSE值随时间的变化Fig. 7 Comparison of root mean square error (RMSE) between calculated values and corresponding Dean curvesa. 滩肩补沙；b. 沙坝向海侧补沙a. Berm nourishment; b. bar nourishment to the seaward

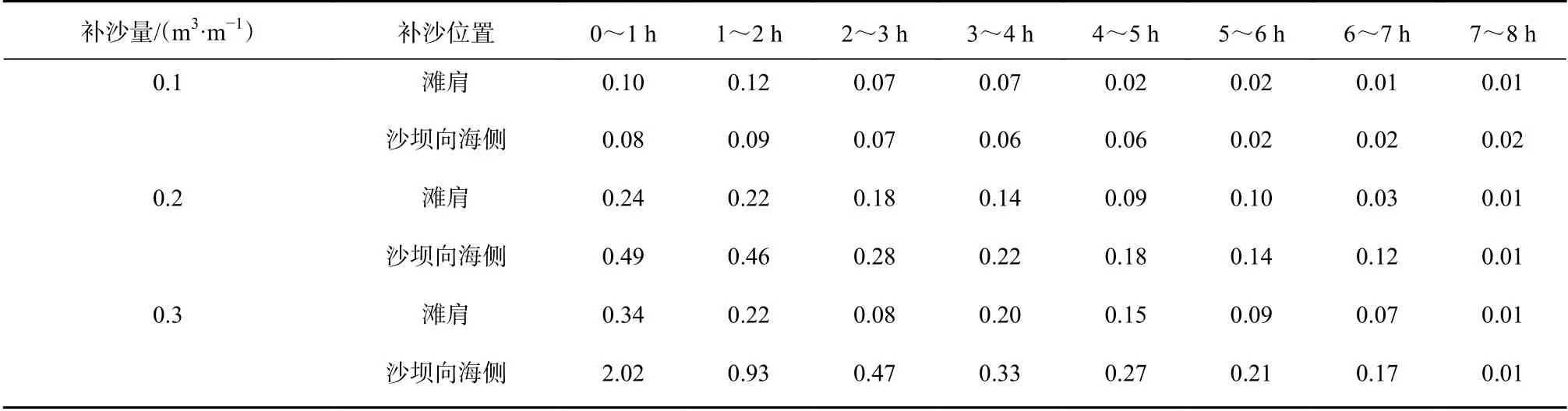
表4 模拟工况0～8 h内RMSE值变化率（单位：10−2 m/h）Table 4 The change rate of RMSE value within 8 hours of simulation cases (unit: 10−2 m/h)

根据工程经验总结，人工补沙的基本功能有：提高海岸稳定性、增强海岸防护以及增宽海滩宽度[23]。一般来说，可以通过长时间波浪作用下的海滩剖面变化来评价人工补沙的长期效果。除此之外，在工程实际中存在遇到强风暴的可能性，应在短期且迅速的风暴过程中评估人工补沙抵御风暴的能力。因此，本文分别模拟了未补沙剖面和补沙剖面在一次风暴后的床面高程变化，补沙工况为B4至B6，C4至C6，波浪条件见表3；并分别对比了不同补沙量下两种补沙位置在风暴前后的剖面变化，图8a、图8c、图8e为滩肩补沙3种工况，图8b、图8d、图8f为沙坝向海测补沙工况。表5中列出平均水位以下Y为0.43～0.50 m范围内海滩向海边缘水平方向淤积/蚀退距离，表6列出X为15.5～16.4 m范围内的水下凹槽位置的高程变化。

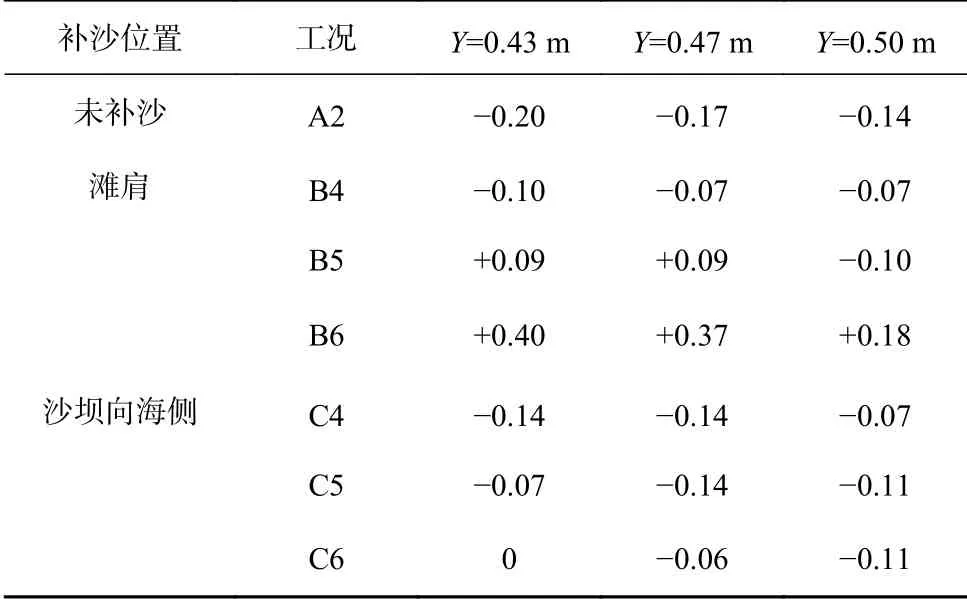
表5 风暴后海滩边缘水平位置变化（单位：m）Table 5 Changes of horizontal position of beach edge after storm (unit: m)

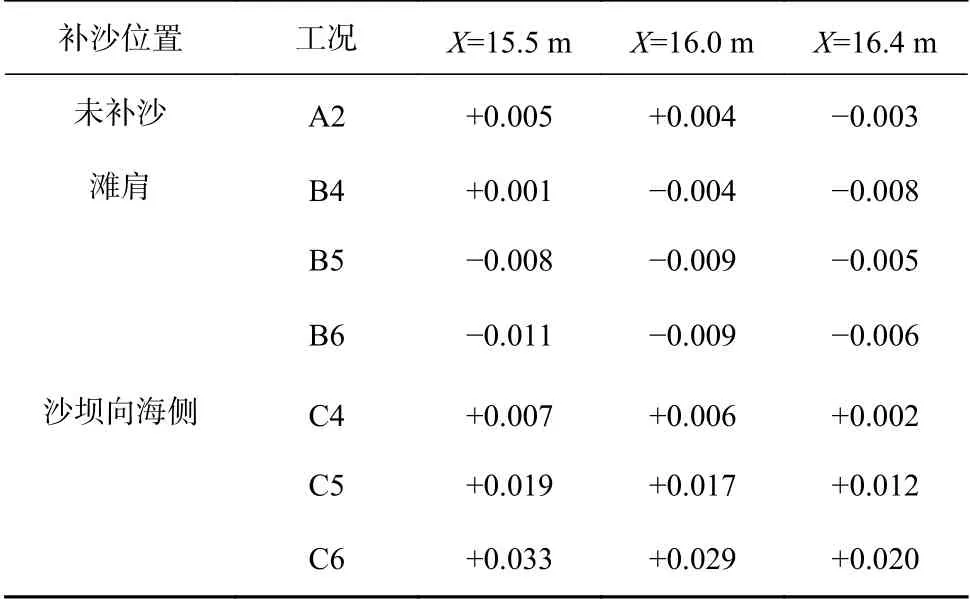
表6 风暴后水下凹槽处床面高程变化（单位：m）Table 6 Changes of bed elevation at underwater trough after storm (unit: m)

将补沙工况与未补沙工况经过风暴30 min后的剖面形态进行对比可看出，滩肩补沙和沙坝向海侧补沙均可减轻滩肩部分侵蚀后退情况，海滩平均水位附近宽度得以维持。根据Collins和Weir[24]得到的经验公式（8）和公式（9）计算可得破碎点位置为0.12 m水深处，如图8中蓝色符号标记点所示。

图8 风暴作用下人工补沙剖面变化Fig. 8 Changes of artificial beach profile under storma. 滩肩补沙（0.1 m3/m）；b. 沙坝向海侧补沙（0.1 m3/m）；c. 滩肩补沙（0.2 m3/m）；d. 沙坝向海侧补沙（0.2 m3/m）；e. 滩肩补沙（0.3 m3/m）；f. 沙坝向海侧补沙（0.3 m3/m）a. Berm nourishment (0.1 m3/m); b. bar nourishment to the seaward (0.1 m3/m); c. berm nourishment (0.2 m3/m); d. berm nourishment to the seaward(0.2 m3/m); e. berm nourishment (0.3 m3/m); f. bar nourishment to the seaward (0.3 m3/m)

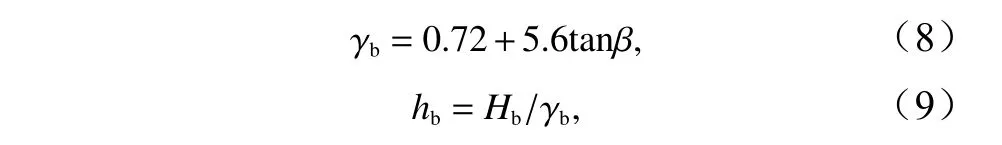
式中，γb为浅水区波浪破碎时的指标；Hb为破碎波高；hb为破碎水深。

由模拟结果可见，滩肩位置补沙对于减轻强浪条件对平均水位附近滩肩部分的侵蚀作用显著，水下岸坡略有堆积；在破碎点以内至平均水位与岸滩交界处的海滩宽度增加。3种滩肩补沙工况水下剖面形状未改变，破碎点位置均位于14.4 m处。当补沙量为0.1 m3/m时，全部补沙体位于平均水位以上，水下坡度为原剖面坡度，因此波浪破碎位置同未补沙工况相同，所形成的水下剖面形状也相同，平均水位附近的滩面侵蚀程度较未补沙工况有所减轻。随着滩肩补沙量增加，补沙体向海延伸，而由于波浪破碎位置未发生变化，波浪破碎点与补沙体向海侧的距离减小，但到达补沙体的波浪能量仍较大，因此受到的侵蚀作用较强，补沙体被侵蚀的泥沙量增加；在平均水位附近，波浪破碎后引起强烈紊动，波浪上爬直接冲刷补沙体向海侧，在上冲水流和下冲水流作用下部分泥沙被侵蚀，其中推移质在破碎点以内至平均水位与岸滩交界处堆积，滩面向海淤进，悬移质被带到破碎点之外堆积。

沙坝向海侧补沙同样也可减轻滩肩部分的侵蚀程度，但效果不及滩肩补沙显著。由于在原剖面的沙坝向海侧补沙，形成的新的水下沙坝位置较未补沙工况更远，波浪破碎点提前，因此对后方剖面有一定的掩护作用。由于水下补沙体的存在使得补沙处的水深变浅，波能损耗，作用在滩面上的波浪能量减弱，被波浪破碎扰动的泥沙中推移质向岸移动，增加水下凹槽处的高程以及减小滩肩部分的蚀退宽度，一部分泥沙被带到沙坝向海侧堆积，进一步削减波能，并且随着补沙量的增多，水下补沙体高度增加，消能作用增强。两种位置比较而言，滩肩补沙对于平均水位以上部分海滩防护效果显著，对于水下部分作用较小；沙坝向海侧补沙对于水下部分海滩剖面的作用效果更为明显。

5 结论与展望

本文通过建立XBeach一维海滩剖面演变模型进行数值模拟，对不同补沙方案在常浪下的补沙效率和风暴作用下的防护效果进行对比分析，以综合评价不同补沙方案对海滩剖面的影响。分析发现，补沙量较少时，滩肩补沙使得海滩较快到达平衡剖面，补沙效率高于沙坝向海侧补沙工况，对于滩肩的防护和恢复效果较好，可以直接地扩宽或加高海滩，但对于水下形成的侵蚀凹槽补充效果缓慢。当补沙量较多时，选择在沙坝向海侧补沙能够促进海滩更快地接近平衡剖面，缩短到达平衡的时间，其补沙效率优于滩肩补沙工况。同时，水下补沙体可充当水下沙坝，从而起到削弱波浪能量、减小波高的作用，在风暴下对海滩整个剖面的防护较好，有利于水下剖面的恢复。

本文采用Dean平衡剖面作为补沙后剖面到达平衡的判断依据，并未充分考虑复杂多变的海洋环境条件。因此，在后续的研究中将对实测海滩平衡剖面进行更多的探讨。同时，本文的数值模拟是对小尺度物理模型试验进行工况的补充完善，进而对泥沙重新分布规律进行探讨。但由于海洋环境条件的复杂多变以及泥沙运动规律的复杂性，对于实际尺度的海滩演变仍需进行大量现场实测以及大型物理模型试验，结合数值模拟，对海滩养护后泥沙运动规律进行更加深入的研究，使实际海滩养护工程达到最佳效果，提高工程效率，为实际补沙工程提供理论依据和技术支撑。