波浪作用下海床孔压累积过程离散元数值模拟

2021-12-13王岳刘春刘晓磊刘辉李亚沙

海洋学报 2021年11期

王岳，刘春*，刘晓磊，刘辉，李亚沙

( 1. 南京大学地球科学与工程学院，江苏南京 210023；2. 中国海洋大学环境科学与工程学院，山东青岛 266100)

1 引言

黄河口海床沉积物工程地质特性复杂，土体以粉质土为主，易液化。在风暴潮期间，波浪对土体施加巨大的循环荷载作用，造成海床土体孔压累积，并发生一定程度的液化，进而诱发海床表层出现滑坡、塌陷凹坑等灾害，直接威胁到海上工程如石油平台、海底管线等构筑物的安全稳定，最终造成巨大的经济损失[1]。

黄河口海床沉积物孔压累积问题已成为国内外海洋工程及地质工程领域研究的热点问题。已有大量学者对波浪作用下海床孔压响应机制进行了研究，Anderson等[2]基于波浪水槽实验对冲浪带沙洲上波浪引起的孔压梯度和床位响应进行了观测研究；Niu等[3]在宽波浪水槽中进行了一系列实验，研究了随机波浪作用下粉质海底的孔压响应；常方强和贾永刚[1]在黄河口海床若干深度处埋设孔压探头，研究黄河口原状和重塑粉质土在波浪循环荷载作用下的液化特征；刘晓磊等[4]在现代黄河水下三角洲潮间带岸滩进行现场试验，测定黄河口原状海床沉积物在循环荷载作用不同阶段的孔压响应与强度变化；张少同等[5]研究了黄河现代三角洲沉积物的堆积、固结、液化、侵蚀再悬浮、海床变形滑动及后期改造等一系列动态变化过程；吕豪杰等[6]基于改造的圆筒试验设备，通过加载装置控制模型土体上方的波压力，实现了波浪荷载作用下的桩周土体孔压响应模拟；宋玉鹏等[7]在黄河口使用自行研发的孔压监测设备对海底粉土孔压力进行了有效监测。

在试验研究的基础上，数值模拟是探究海床孔压响应机理的重要方法。例如，吴雷晔等[8]通过与离心模型试验数据的对比，验证了基于Biot固结理论及“交变移动”土体本构模型的数值分析方法对波浪作用下海床液化问题模拟的有效性；潘冬子等[9]结合波浪槽模型试验研究的结果，提出了一种粉质海床在波浪作用下超静孔压增长的有限差分数值分析方法，并揭示了粉质海床孔压发展的机理；刘涛等[10]采用有限差分法，对波浪作用下孔压响应进行了数值计算，发现海床中由波浪引起的超孔压随深度分布不均匀，存在极值点，并且孔压响应存在滞后效应；周援衡等[11]采用Biot固结理论分析了海床沙层对波浪荷载的响应，用有限元数值模拟法得到沙床中孔压分布，数值计算结果与实测结果吻合良好。

前人对波浪作用下海床沉积物孔压响应问题开展了大量的试验研究，并采用有限差分法、有限元法等数值方法，较好地模拟了孔压的累积过程。但是这些方法难以模拟岩土体的离散性以及孔压累积造成的土体破坏和灾害效应。本文基于非连续的离散元法和多孔介质孔隙网络模型，提出离散元孔隙密度流方法，实现渗流和流固耦合模拟。基于现场试验装置和数据，建立了相应的离散元数值模型，对波浪作用下海床孔压累积过程进行了模拟分析，探究了孔压累积规律和机理。并进一步模拟了周期性波浪荷载作用下土颗粒液化悬浮过程。

2 离散元法基本原理

在离散元法中，岩土体模型由一系列遵循牛顿运动定律的颗粒堆积组成（图1）。颗粒间通过弹簧力相互作用，两颗粒间的法向力（Fn）由下式给出[12]：

图1 离散颗粒堆积模型（a）、颗粒间法向弹簧力（b）和颗粒间切向弹簧力（c）Fig. 1 Packing model of discrete element (a), normal spring force between particles (b), and shear spring force between particles (c)

式中，Kn为法向刚度；Xn为法向相对位移；Xb为断裂位移。初始时，颗粒与其相邻颗粒相互连接，受拉力或压力作用（式（1a），拉力为正）。当两颗粒之间的Xn超过断裂位移时，弹簧断裂，颗粒间拉力消失（式（1c）），仅存在压力作用（式（1b））。

颗粒间通过切向弹簧来模拟剪切变形和切向力，剪切弹簧的切向力（Fs）通过下式决定：

式中，Ks为切向刚度；Xs为切向相对位移。对于完整的颗粒连接，其最大切向力（Fsmax）由摩尔库伦准则确定：

式中，Fs0为颗粒内部的抗剪力；μp为摩擦系数。当颗粒受切向外力超过式（3）中的Fsmax时，颗粒间连接断裂，单元连接允许的最大切向力F'smax为

当外力超过最大摩擦力时，两相邻颗粒开始滑移，滑动摩擦力等于F'smax。

在数值模拟中，单元所受合力为弹簧力、阻尼力和重力等的矢量和。假定在非常小的时间步内，单元的速度和加速度不变，基于时间步迭代算法和牛顿运动方程实现离散单元的动态模拟[12]。

3 离散元孔隙密度流法

基于传统的岩体孔隙网络模型[13]，本文提出了离散元孔隙密度流法来实现岩土体流固耦合的高效计算，这种方法的基本步骤为：（1）利用离散元堆积颗粒建立孔隙流体域（图2b）；（2）通过孔隙流体密度和温度来确定孔压，在孔隙间采用类似于达西定律的方法计算渗流；（3）将孔压作用于固体颗粒，实现流固耦合模拟。

如图2a所示，经过离散元计算获得离散元堆积颗粒后，根据颗粒间的接触关系，通过连接相邻颗粒的中心点，在堆积模型中剖分出一系列相互连通的流体域。建立以孔隙流体域单元为节点，孔喉通道相连接的孔隙流体域（图2b），最后得到颗粒−孔隙系数（图2c）。

图2 离散元堆积颗粒（a）、孔隙流体域（b）和颗粒−孔隙系统（c）Fig. 2 Discrete element stacked particles (a), pore fluid domain (b), and particle and pore system (c)

数值模拟假定孔隙均为饱和状态，孔隙流体压力ρ可以由孔隙流体密度ρ和温度T来确定[14]：

根据已知的饱和水蒸气压、温度、密度数据拟合得到水温为20℃时，孔隙流体压力与孔隙流体密度的关系[15]为

如图3所示，当两相邻孔隙间存在压力差时，流体将通过二者间的孔喉通道发生渗流，其渗流量可通过类似达西定律的方法来计算。本文中，在单位时间内通过孔喉的流量（q）定义为

图3 颗粒微观渗流示意图Fig. 3 Schematic diagram of particle microscopic seepage

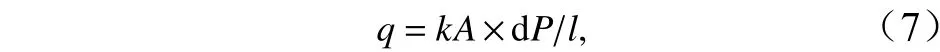
式中，k为孔喉的渗透系数；A为孔喉通道面积；dP为孔喉间压力差；l为孔喉长度。两颗粒半径分别为R1、R2；两颗粒中心的距离为L；孔喉长度l定义为

对于二维问题，单位宽度孔喉通道面积可用孔喉的直径（dw）表示。由于二维颗粒堆积通常会封闭孔喉，从而使孔喉直径为0，导致无法发生渗流。因此，在进行二维模型渗流计算时，需要给每个单元定义较小的渗流作用半径（Rw），默认取单元半径的0.975倍，从而保证一定的孔喉直径，并使流体能够通过孔喉运移。孔喉直径（dw）定义为

式中，Rw1和Rw2分别为单元1和单元2的渗流作用半径。

以上计算中，流体在孔隙间压差驱动下运移，实现了渗流模拟，进一步实现流固耦合作用，将流体压力作用在单元上，并获得流体对单元的合力。通过常规离散元法计算单元运动，实现流体对固体的作用。同时，当单元运动后，孔隙的体积变化，需计算孔隙密度，并根据公式（5）获得孔隙新的压力，从而实现固体对流体的作用。最后，根据单元坐标划分新的网格，并更新网格中的流体属性，再返回到渗流计算。

4 离散元建模与数值模拟

4.1 建模与赋材料

本文依据常方强和贾永刚[1]在黄河三角洲现行的清水沟流路南部的潮间带上开展的现场试验，实现了波浪作用下海床孔压累积过程的离散元建模与数值模拟。现场试验装置主要包括加载系统和孔压监测系统，加载系统采用自制活塞式压水方式，主要由圆柱形铁桶、活塞和手柄组成；孔压监测系统由孔压探头、多通道数据采集系统、通讯电缆和计算机组成。

根据现场试验装置，利用MatDEM进行建模[16]。第一步先建立长、高为0.5 m×1 m的模型箱，向模型箱内随机添加平均半径为0.005 m的颗粒，总颗粒数为5629，颗粒经过重力沉积和压实作用，最终形成颗粒堆积模型（图4）。

图4 颗粒堆积模型Fig. 4 Particle accumulation model

第二步再给模型赋材料，根据现场试验[1]及经验得到海洋土体宏观力学性质（表1），基于宏微观转换公式[12]和MatDEM自动训练模块，软件自动训练得到符合宏观要求的离散元材料，具体离散元微观力学参数见表2。

表1 海洋土体宏观力学性质Table 1 Macro mechanical properties of ocean soil

表2 离散元微观力学参数Table 2 Micro mechanical parameters of the discrete element

第三步将模型箱上部0.2 m范围内的颗粒筛选出并删除，建立海床表面的流体域。根据土体渗透率确定微观渗透系数，并计算出模拟海床沉积物渗透系数K为1.32×10−5cm/s，数值在现场试验测得的数据范围内。

4.2 数值模拟计算

现场试验利用人工操作活塞施加水压循环荷载以模拟波浪荷载，循环荷载控制在0～4 kPa，加载周期为6.67 s，循环加载40次，观察孔压累积规律。同样地，在数值模拟中，对海床流体域施加0～4 kPa循环荷载，模拟波峰、波谷的作用。模拟设定时间步为6.67×10−4s，每个周期迭代计算10000次，实现加载周期6.67 s。循环加载40次，模拟现实时间266.8 s，其时间段与现场试验分析时间段一致。

现场试验分别将孔压探头埋设在深度为5 cm、8 cm、12 cm、20 cm和30 cm处，因此在离散元模型内选取土体深度为0.05 m、0.08 m、0.12 m、0.20 m、0.30 m、0.40 m和0.5 m的位置，对应于现场试验，记录不同深度土体孔隙水压力，并进一步用于绘制孔压分布图和孔压累积过程图。

5 模拟结果与分析

5.1 单周期波浪荷载下的孔压变化特征

图5显示了施加荷载1个周期内，不同深度土体孔隙水压力随时间变化曲线。图中黑色实线代表数值模拟时，施加于海床表面流体域上即深度为0处用来模拟波浪作用的荷载，增加循环次数可模拟正弦荷载作用。

图5 单周期荷载下孔隙水压力变化趋势Fig. 5 Trend of pore water pressure under single-cycle loading

前T/2时间内施加最大荷载4 kPa，在荷载作用下，各深度土体颗粒间逐渐产生孔隙水压力。深度为0.05 m时土体最先产生孔压，由于波浪直接作用于表层土体，而水下土体处于完全饱和状态，当受到荷载作用时，表层土颗粒间的水最先受到挤压，并且不能及时排出，从而导致表层土体最先产生孔压。在渗流作用下，孔压逐渐向深层传递，由于渗流需要一定的时间，因此土体深度越大，渗流时间所需越长，所以，土体孔压增大速率随深度增加而降低。

后T/2时间内施加最小荷载0 kPa，观察到深度为0.05 m时土体颗粒间孔压急剧减小，紧接着深度为0.08 m、0.12 m的土体颗粒间孔压开始陆续减小，且深度越大，减小越缓慢。施加荷载1个周期内，深度大于0.2 m的土体，孔压一直缓慢上升，因为土体深度越大，颗粒间孔压受荷载变化影响需要的时间越长，在6.67 s周期内表现不明显。

施加荷载1个周期后，观察到深度为0.12 m的土体颗粒间孔压最大，表层土体颗粒与波浪直接接触，受荷载作用最明显，在0 kPa荷载作用时孔压减小速率快；荷载减小对深层土体产生影响所需的时间更长，并且上层土体颗粒间孔压减小过程中仍然发生渗流作用，因此深层土体颗粒间孔压减小速率相对较慢。

5.2 循环波浪荷载下的孔压累积过程

为了解周期循环波浪荷载的作用，将施加荷载次数设为40次。图6显示了施加荷载第1个、第10个、第20个和第40个周期后，数值模型中的孔压分布情况，其分别对应于6.67 s、66.7 s、133.4 s和266.8 s 4个时刻。从图中可以看出，随着荷载循环次数增加，孔压累积范围逐渐变宽，孔压最大区域稳定在土体深度0.20 m上下。加载40个周期后，深度大于0.30 m土体孔压基本稳定在1.5 kPa。

图6 荷载循环1次（a）、10次（b）、20次（c）、40次（d）孔压分布Fig. 6 Pore pressure distribution of load cycle 1 (a), 10 (b), 20 (c), 40 (d) times

图7为不同深度土体在荷载循环40个周期内，孔压随时间的累积曲线。从图中可以看出，深度从0.05 m到0.30 m处的孔压均呈现出“边振荡，边累积”的趋势，振荡幅值随着深度的增加而减小。随着孔压累积时间延长，各个深度土体孔压都累积增加[17]，增加速率逐渐降低。

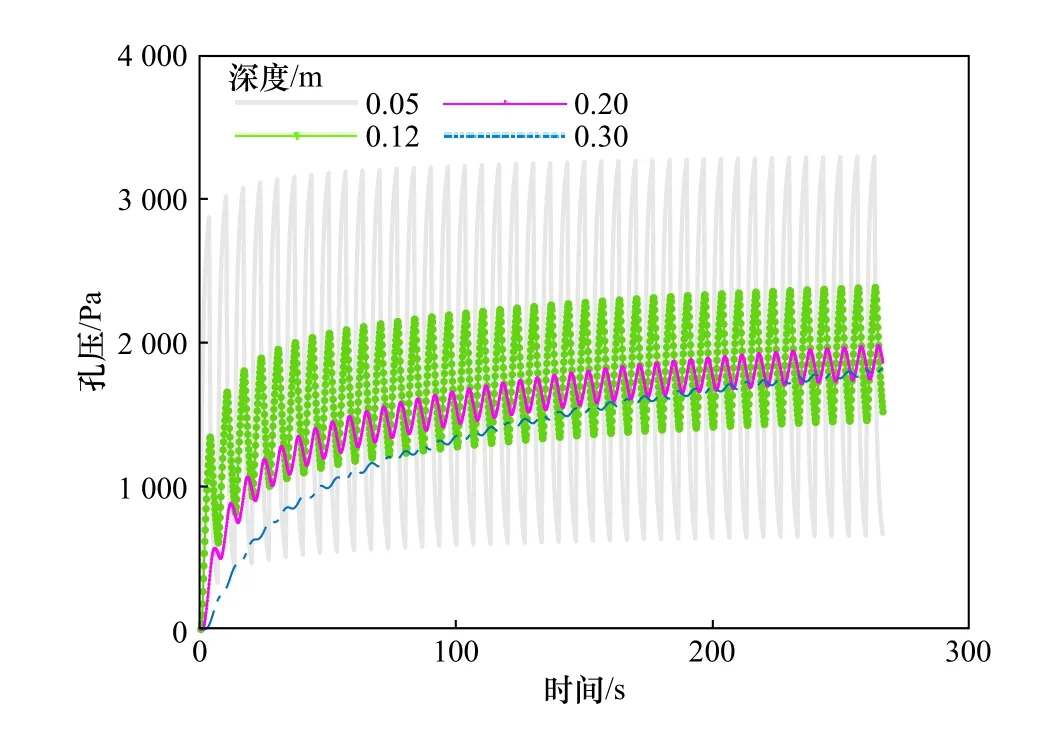
图7 循环荷载40次孔压累积Fig. 7 Pore water pressure accumulation process under cyclic loading 40 times

将孔压累积过程曲线进行拟合，可得到不同土体深度处孔压P与时间t之间的函数关系。土体深度为0.05 m时：

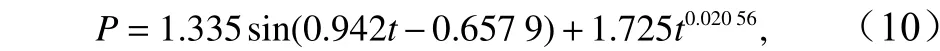
土体深度为0.12 m时：

土体深度为0.2 m时：

土体深度为0.3 m时：

以上公式可归纳为

式中，A为振幅；w为角速度；φ为初相；B为系数；α为指数。

可以看到，孔压累积过程曲线为正弦函数与幂函数的叠加。正弦波的周期与加载周期基本吻合，正弦波振幅A、系数B和土体深度呈负相关，幂函数指数α和土体深度呈正相关。

表3显示了采用数值模拟与现场试验两种方法得到不同深度土体孔压累积266.7 s时的数据对比，此时孔压数据都基本达到稳定。结果显示，数值模拟与现场试验孔压数据接近；累积时间266.7 s后，两者孔压都缓慢上升，呈现出良好的相关性。分析存在细小误差的原因为：数值模拟基于平面应变假设，建立的离散元模型相对均质，而现场试验海床土体较为复杂，可能存在分层，并且其渗透性、密实度等会随深度和孔压的变化而发生变化，因此孔压向深层传递过程会有所差异。导致0.12 m深度误差较大的原因可能是现场试验数据采用人工加载、人工读数，存在偶然误差。

表3 数值模拟与现场试验孔压数据对比Table 3 Data comparison of pore pressure between numerical simulation and field test

继续增加施加荷载次数，当孔压累积时间足够长时（500 s以上）可以发现0.20 m深度的土体孔压最终收敛于所施加最大荷载与最小荷载的平均值（2 kPa）。现场试验测得土体重度为19.8 kN/m3，则土体浮重度r'为10 kN/m3，当施加荷载为0 kPa时，0.20 m深度土体的初始有效应力σ'=r'×h，结果为2 kN/m2。传统土体力学以初始有效应力作为判断海床液化的临界值[18]，在离散元法中同样适用，此时土体孔压将达到初始有效应力，土体开始发生液化，液化一方面会降低海床表层沉积物的抗侵蚀性；另一方面，在海床内部垂向渗流的驱动下，内部部分细粒沉积物会被“泵送”输运至海床表面，进而进入上覆水体成为再悬浮沉积物[5]。

6 海床沉积物液化悬浮模拟

张少同等[5]分析了黄河三角洲沉积物的侵蚀再悬浮过程，波浪循环荷载作用不仅可以导致海床沉积物发生孔压累积、液化破坏、强度弱化甚至丧失，还为沉积物再悬浮提供剪切力，微弱的近底剪切力就能够将强度弱化或完全液化的海底沉积物侵蚀再悬浮。

以上数值模拟研究表明，在波浪循环荷载作用下，海床沉积物内部孔隙水压力发生累积，并逐渐达到液化标准，进而土体颗粒发生液化悬浮。为了进一步分析土体发生液化后的情况，开展了波浪周期性荷载作用下，海床沉积物液化悬浮过程的模拟。

6.1 建模与加载

模拟过程中离散元建模方法同4.1节，为了更接近海海床实际情况，设置模型箱长、高为1 m×0.5 m，随机添加平均半径为0.01 m的颗粒，总颗粒数为1579。加载方式与之前不同，在海床流体域左侧施加4 kPa荷载，相当于实际波高0.80 m的作用效果[4]，线性递减到0 kPa模拟波浪剪切作用。根据5.2节模拟结果，在土体0.20 m深度处施加2 kPa荷载，用来模拟已累积孔压对后续土体孔压累积以及颗粒移动的影响。模拟设定时间步为1×10−3s，每个周期迭代计算10000次，模拟真实世界10 s，得到土体孔压分布和颗粒位移场。

6.2 模拟结果分析

从图8中可以看出，在波浪剪切作用和已累积孔压共同作用下左侧表层土体内积累的孔压较大，为3.5 kPa左右，右侧较小，为0.5 kPa左右，深层土体内孔压累积大小介于两者之间。

图9为数值模拟10 s后土体颗粒位移场，可以观察到深度在0～0.30 m范围内土体颗粒发生剪切位移，结合图8孔压分布可以发现，0～0.30 m土体内孔压累积超过2 kPa，达到液化标准，土体发生液化，在波浪剪切力的作用下，土颗粒悬浮，浅层土体由于直接受到波浪剪切作用，位移量更大，随着土体深度增大，位移量逐渐减小。

图8 孔压分布Fig. 8 Distribution of pore pressure

图9 模拟10 s位移场Fig. 9 Simulation of 10 s displacement field

观察整个模型箱内土体颗粒位移情况，发现海床整体呈现圆弧形移动（图10）。土体液化后土体颗粒间的黏聚力丧失，进而造成海床抗剪性降低，在波浪荷载作用下海床发生圆弧形振荡剪切。由于波浪荷载是循环荷载，呈周期性变化，波峰和波谷交替出现，在海床内引起的循环应力呈现相反的方向变化，为振荡剪切破坏创造了条件。随着波浪周期性荷载的持续作用，土体液化深度增大，振荡面向更深层延展，最终破坏稳定在一定深度[15]。