采用多层卷积稀疏表示的红外与可见光图像融合
2021-12-13张洲宇曹云峰
张洲宇,曹云峰,丁 萌,陶 江
(1.南京航空航天大学 航天学院,南京 210016;2.南京航空航天大学 民航学院,南京 211106)
由于传感器成像特性的差异,红外传感器与可见光传感器拍摄的图像往往具有较强的互补性[1]。红外图像在低能见度条件下依然可以清晰的捕获目标,但是图像的边缘、纹理等细节不够丰富。可见光图像具有较强的细节保存能力,但是成像质量极易受到光照变化的影响。为了最大程度地结合两种图像类型的优点,将红外图像与可见光图像进行融合从而弥补传感器的固有缺陷成为了一条行之有效的思路。红外图像与可见光图像融合目前已广泛地应用于智能监控、目标监视、视频分析等领域[2]。
现有的图像融合算法根据所选取的融合信息可分为像素级、特征级、决策级3个层级,其中像素级图像融合直接对源图像进行融合,所保存的细节信息最为完备,因此在过去数十年中得到了广泛的关注[3]。像素级图像融合又可以进一步分为空间域融合与变换域融合两类,空间域融合无需对图像进行任何变换操作,因此实现较为简单,但是易于导致融合图像低对比度及块状分布等缺陷。为了克服上述不足,变换域图像融合采取的方案是对源图像进行适当的图像变换,并对转换后的图像信息进行融合。变换域图像融合的基本流程分为:1)图像变换,将源图像由空间域映射到变换域;2)活性度衡量,衡量变换后向量的重要程度;3)融合规则设计,采取恰当的融合规则完成活性层的筛选。显然,变换域图像融合的核心在于由空间域到变换域的变换方式[4]。
早期的变换域图像融合所采取的变换方法包括小波变换、金字塔变换等,通过人工构建的小波基与金字塔基实现源图像的变换。由于人工构建的图像变换的图像表示能力始终有限,该类方法始终难以获取图像中所有隐藏的信息。为克服早期图像变换的局限性,压缩感知(compressive sensing,CS)理论通过预训练的过完备字典实现源图像的变换,由于过完备字典是从大量的训练样本中学习得到的,CS理论的图像表示能力具有显著的优势,在过去10年中受到了广泛的研究[5]。基于CS理论的图像融合方法可分为3个步骤:首先将源图像分解为若干均等大小的图像块,对每一个图像块利用预训练的过完备字典计算与其对应的稀疏向量;其次,对同一位置对应的稀疏向量进行融合,获取融合后的向量;最后,利用融合后的向量结合过完备字典完成融合图像的重建。CS理论应用于图像融合最大的不足在于:1)基于图像块的建模方式破坏了源图像的语义结构,难以有效提取源图像中包含的空间上下文信息。2)基于图像块的建模、融合与重建对于两幅图像的匹配关系提出了严苛的要求,因此对于误匹配的容忍度较低[6]。为克服上述不足,近年来的相关研究工作开始尝试使用全局建模的方式对源图像进行变换,其中最为有效的变换方式为卷积神经网络(convolutional neural network,CNN)与卷积稀疏表示(convolutional sparse representation,CSR)。
CNN根据所需解决任务属性的不同可以分为分类式CNN与回归式CNN两类[7]。分类式CNN目前已在视觉目标检测、识别与分类等任务中得到了广泛应用,传统的视觉识别流程总体上可分为3个步骤,即特征表示、特征选取与特征分类,分类式CNN最大的优势在于通过多层卷积神经网络将上述3个步骤联合实现[8-12]。Liu等[4]指出,早期的变换域图像融合方法所包含的3个步骤与传统视觉识别的3个步骤具有极大的相似性,因此将分类式CNN应用于图像融合成为了一条可行的思路。回归式CNN又称为全卷积神经网络(fully convolutional neural network,FCN),一般采用端对端的方式实现视觉信息的分析与处理。回归式CNN目前已在低级视觉任务中得到了大量应用,例如图像分割、超分辨率重建等。因此,如果给定融合图像的真值图,即可训练回归式CNN通过端对端的方式获取融合结果。然而,无论是分类式CNN还是回归式CNN,其共性不足在于难以获取大量带标签的训练样本用于网络训练[13]。
CSR的基本思路源于Zeiler等[14]所设计的反卷积网络,其目的在于通过非监督的方式从自然图像中提取中级与高级特征。CSR的基本原理是通过一组预先训练的卷积字典滤波器将源图像分解为一系列卷积稀疏响应图,每一张卷积稀疏响应图都包含了目标不同层级的信息。作为一种非监督机器学习方法,CSR已被成功地用于解决许多视觉处理任务,例如目标跟踪、背景建模以及图像去噪等。在图像融合领域,CSR可以视为一种有效的图像变换方法[15]。由于CSR的图像建模方式无需对源图像进行分解,避免了基于稀疏表示(sparse representation,SR)的图像融合算法[3]的局部建模所带来的语义信息缺失与对误匹配的低容忍度两大缺陷,因此CSR已在图像融合领域得到了成功的应用。Zeiler等[14]指出,当基于CSR的反卷积网络的层数加深时,网络学习得到的图像特征将由边缘向整个目标转移,考虑到红外与可见光图像融合的初衷在于凸显源图像中的目标,为此本文设计了一种面向红外与可见光图像融合的多层卷积稀疏表示网络。
1 面向红外与可见光图像融合的多层卷积稀疏网络结构
本文所设计的面向红外与可见光图像融合的多层卷积稀疏网络如图1所示,该网络共包含5层,采用前馈的方式实现红外与可见光源图像的融合。

图1 基于多层卷积稀疏表示的红外与可见光图像融合网络
网络的第1、2层为卷积稀疏层,通过预先训练的多层字典滤波器将源图像变换为一组卷积稀疏响应图。网络的第3层为融合层,通过对活性度衡量以获得卷积稀疏响应图的融合结果。网络的第4、5层为重建层,通过融合后的卷积稀疏响应图结合预先训练的多层字典滤波器实现融合图像的重建。
相比于SR、CSR、CNN等现有图像融合方法,本文所设计的图像融合网络具有以下优势:
1)与SR的局部变换方式不同,本文所设计的图像融合网络采用全局变换的方式,有效抑制了SR应用于图像融合所导致的语义信息损失以及对细节信息的低容忍度两大缺陷。
2)相比于基于CSR的图像融合方法,本文借鉴了卷积神经网络的设计思路。Papyan等[16]通过理论分析已经证明了多层卷积稀疏表示网络与CNN的结构存在着紧密的联系,多层卷积稀疏表示可以实现更有效的图像变换。
3)区别于CNN的监督学习特性,本文所设计的多层卷积稀疏网络采取的学习方式是非监督的,无需大量带有标签的训练样本完成网络的训练,在实现上更为简单。
4)本文算法的计算复杂度相比于SR具有明显的优势,相比于CSR不会明显上升。假设SR与CSR所使用的字典维度均为k,输入图像的大小均为D×D,基于SR的图像融合方法计算复杂度为O(D2×k2);基于CSR的图像融合方法计算复杂度为O(k×D×log(D)),明显低于SR的计算复杂度[17];本文算法共包含两层卷积稀疏层,因此计算复杂度为O(2k×D×log(D)),较CSR更高,但依然低于SR。
2 基于多层卷积稀疏表示的红外与可见光图像融合算法
2.1 多层卷积稀疏表示理论
给定输入图像I∈RA×B,以及一组相同大小的图像滤波器fi∈Ra×b,i=1,2,…,m,这样一组滤波器被定义为卷积字典滤波器。CSR的基本思想在于任意一幅输入图像I都可以表示为卷积字典滤波器以及与之对应的卷积稀疏响应图si∈RA×B,i=1,2,…,m乘积的和。CSR的目标函数如下式所示:
(1)
式中λ为稀疏正则项。
由于卷积稀疏响应S可被视为m张大小为A×B的图像集合,S中的每一张卷积稀疏响应图可以进一步地被另一个卷积字典滤波器F′∈Ra′×b′×m′和与之对应的卷积稀疏响应图表示,以此类推,可获得K层的卷积稀疏响应图。如定义1所示,这种类型的CSR被称为多层CSR。压缩感知理论的基本思想可视为通过对过完备字典D中原子的组合来表示输入信号,多层CSR的基本思想与压缩感知理论相似,但是区别于压缩感知理论所用到的字典原子,多层CSR用于表征信号的是采用多层字典的复杂组合Dl1Dl2…DlK,与压缩感知理论中的字典原子对应,这一类的字典组合被称为“分子”[16]。

……

(2)
式(2)可视为经典的基追踪问题的卷积形式,可通过交替方向乘子算法(Alternating direction method of multipliers,ADMM)有效求解。
为了引入ADMM求解式(2)的优化问题,将式(2)转换为如式(3)所示的交替形式,对式(3)的优化过程通过迭代的方式进行,从第t步至第t+1步的迭代如式(4)~式(6)所示:
(3)
(4)

(5)
(6)
式中u为引入的辅助变量。

(7)
(8)

(9)
(10)
(11)
2.2 多层卷积字典学习

(12)

(13)
(14)
(15)
C={x∈RA×B:(I-PPT)x=0,‖x‖2=1}
(16)

(17)
通过引入辅助变量h以及参数ρ,式(15)可以改写为式(18)的形式从而采用ADMM求解,从第t步至第t+1步的迭代过程如式(19)~式(21)所示。
(18)

(19)

(20)
(21)


(22)

(23)


(24)
(25)
(26)
至此,多层卷积字典学习的定义归纳如下。

……

2.3 红外与可见光图像融合算法
如图1所示,给定一组配准后的红外图像IIN与可见光图像IVI,本文所设计的图像融合网络共包含5层,以前馈的方式实现。

(27)
(28)

(29)
最终,第4、5层的重建层利用预先训练的卷积字典逐层地重建恢复融合图像,第4层的重建过程如式(30)所示,第5层的重建过程如式(31)所示。
(30)
(31)
至此,基于多层卷积稀疏网络的红外与可见光图像融合算法归纳如下。

3 实验分析与验证
3.1 实验设置
如图2所示,3组配准后的红外图像与可见光图像被选为实验用源图像。为了衡量图像融合的实验结果,本文采用主观评价与客观评价相结合的方式来评判融合结果的优劣。主观评价单纯依靠人眼衡量融合结果,而客观评价通过一系列图像质量的评价指标来衡量融合结果。本文所选取的图像质量评价指标包括空间频率(spatial frequency,SF),熵(Entropy,EN),互信息(mutual information,MI)以及梯度评价指标QAB/F,各项评价指标的含义如下:
1)SF代表融合结果的清晰度与纹理丰富度,SF越高,融合效果越好。
2)EN代表融合结果包含的信息量与纹理,EN越高,融合效果越好。
3)MI代表融合结果的互信息,MI越高,融合效果越好。
4)QAB/F代表融合结果的梯度信息,QAB/F越高,融合效果越好。

图2 实验图像
3.2 参数学习与分析
对于本文所设计的多层卷积稀疏表示网络而言,预训练的卷积稀疏字典对于网络的融合效果有着至关重要的影响,因此有必要针对字典的选取对网络融合效果的影响展开分析。由上一节的理论分析可知,给定训练样本,学习参数λ,迭代次数t,卷积字典的长度与卷积字典的大小对于卷积字典的学习有重要的影响。本文用于第1卷积稀疏层的训练样本为200幅自然图像,用于第2卷积稀疏层的训练样本为200幅卷积稀疏响应图,学习参数λ,迭代次数t设置为500。
3.2.1 卷积字典的尺寸对融合效果的影响
如表1所示,当第1、2卷积稀疏层的卷积字典长度固定为32时,卷积字典的大小取值为8×8,16×16,32×32和64×64。由于第2卷积稀疏层的卷积字典训练样本为卷积稀疏响应图而非自然图像,因此可以直观地看出Dl2比Dl1更稀疏。

表1 不同尺寸的卷积字典
源图像1,2,3在不同尺寸字典下的图像融合客观评价指标如图3~5所示。由图中结果可知,Dl1中字典尺寸变化带来的影响较Dl2更大,导致该现象的原因是:1)在字典训练的迭代次数一致的前提下,当字典的尺寸增大时,对于源图像变换的重建误差将随之上升,从而影响最终图像融合的效果;2)与卷积神经网络类似,浅层的网络对于提取图像的边缘信息更有效,且底层网络所提取的边缘信息是后续网络提取语义信息的基础,因此第1层的重建误差将传播至第2层,影响最终的图像融合结果。

图3 源图像1在不同字典尺寸下融合结果的客观评价指标

图4 源图像2在不同字典尺寸下融合结果的客观评价指标
3.2.2 卷积字典的长度对融合效果的影响
如表2所示,当第1、2卷积稀疏层的卷积字典尺寸固定为16×16,卷积字典的长度为16,32,64和128。源图像1,2,3在不同尺寸字典下的图像融合客观评价指标如图6~8所示。由图中结果可知,相比于卷积字典的尺寸,卷积字典的长度对融合结果的影响较小。当卷积字典的长度增加时,图像融合的效果会有微弱的改善,且Dl2对融合结果的影响较Dl1更大。上述现场产生的原因为:1)图像变换对于信息的表示能力极大地取决于特征的维度,而多层CSR的特征维度与字典的长度紧密相关,因此当字典长度增加时,融合效果会有相应的改善;2)与CNN的结构类似,从网络深层提取的信息相较于浅层信息的表示能力更强,因此Dl2对融合结果有更大的影响。
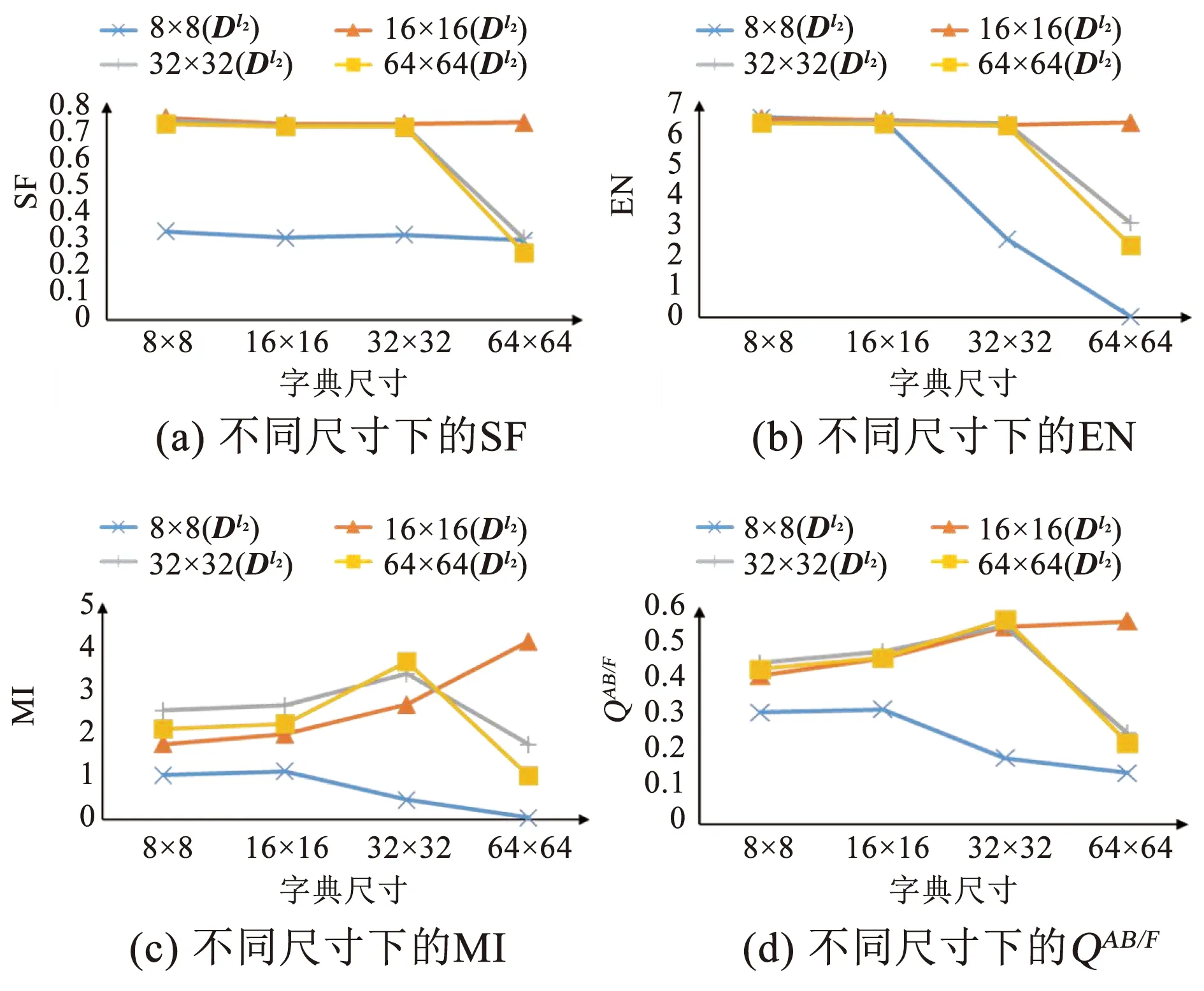
图5 源图像3在不同字典尺寸下融合结果的客观评价指标

表2 不同长度的卷积字典
3.3 对比实验分析
本文采用了3种经典的图像融合算法与本文设计的算法进行对比,3种对比算法分别是:基于稀疏表示(SR)的图像融合算法[3],基于卷积稀疏表示(CSR)的图像融合算法[15],基于卷积神经网络(CNN)的图像融合算法[9]。每一种融合算法所对应的融合结果刚见表3,根据融合结果采用主观评价可知,本文所设计图像融合算法获得的结果在保留细节(例如可见光图像中的植被、建筑等)的同时显著增强了图像中的目标。

图6 源图像1在不同字典长度下融合结果的客观评价指标

图7 源图像2在不同字典长度下融合结果的客观评价指标

图8 源图像3在不同字典长度下融合结果的客观评价指标

表3 融合结果对比
进一步对本文所设计的算法进行客观评价,客观评价指标对比结果如图9所示。由客观评价指标的计算结果分析可知,本文所提出的图像融合算法相比于同类算法具有一定的优势。

图9 不同方法的融合结果客观评价指标对比
针对3组实验图像,对4种算法的实时性进一步进行验证分析。本文的算法实现平台为Matlab 2016b,计算机主频为3.4 GHz,内存为8 GB,采用Matlab的tic toc命令,对于4种算法的运行时间进行统计,统计结果见表4。由表4可知,本文算法相比于SR和CNN在计算时间方面具有明显的优势;相比于CSR,由于前馈式的网络结构导致需要进行两次卷积稀疏运算,因此计算时间略有增长。

表4 融合计算时间对比
4 结 论
1)本文设计了一种多层卷积稀疏表示网络,且给出了针对该网络的卷积稀疏字典训练方法与卷积稀疏响应图求解方法,作为一种有效的图像变换方法,该网络不仅可用于红外与可见光图像融合,同样可被扩展于目标检测、跟踪等领域。
2)与基于稀疏表示的图像融合方法对比,本文所设计的多层卷积稀疏表示网络所具备的全局建模能力在误匹配条件下具有明显的优势。
3)作为一种基于非监督学习的融合网络,本文所设计的图像融合方法无需大量带有标签的训练样本即可完成参数的学习,因此该网络同样可被用于解决其他类型的图像融合问题,例如多焦点图像融合、医学图像融合等。
