基于随机森林的基坑监测数据填补对比研究

程 亮

（北京市地质勘察技术院，北京 100143）

基坑监测作为保证基坑工程安全、深入研究基坑结构动态的重要方法，贯穿于整个基坑工程全寿命周期。基坑监测工作过程中收集了大量数据，但受多方面因素影响，基坑监测数据集经常会发生不同程度数据缺失的情况（张军舰等，2020）。开展数据缺失的识别及填补方法的研究，对于完善监测数据集具有显著意义。

缺失数据填充方法较多，可基于回归分析法、聚类分析法及神经网络算法等多种方式进行填补。雷峰津等（2020）基于电网电能质量监测分析系统提出了一种基于相关分析的缺失数据填充方法，通过分析找到与采样周期一致的强相关性指标，然后使用分段回归的方法建立回归模型。林枫等（2020）基于布谷鸟算法，研究提出了优化的K_means 聚类填充算法。王磊等（2020）采用基于图像数据结构可视化的相关技术，应用小波变换与快速行进算法进行电成像数据空白带填充和响应畸变修复，也取得了良好效果。分段回归的方法准确度较高，但是运行效率相对较低。布谷鸟算法优化的K_means聚类算法是对传统聚类算法的优化改进，一定程度上解决了聚类算法无法度量缺失数据间的相似性问题。小波变换与快速行进算法主要应用于电成像测井数据处理，取得了不错的效果。

针对基坑监测数据的差异化特点和缺失值产生原因，应结合工程实际情况进行针对性的分析，进而从数据自身出发，选择最为恰当的填充方法，并对采用的数据填充方法给出适用性的解释（施虹等，2020）。随机森林方法作为一种集成学习方法，有学者将其利用在结构损伤识别方面，可高准确率识别多种脱空工况（谢坤明，2020），在我国陕北黄土高原典型黄土地貌区域的地貌分类中也取得了较好的结果（曹泽涛等，2020）。本文主要研究应用随机森林模型进行数据填充的方法，探讨了方法的适用性，并与其他填充方法进行对比分析，以期达到合理、高效地填充基坑监测缺失值的目的。

1 工程概况

某基坑工程基坑面积约54000 m2。其中包含8栋主楼及其裙楼，地下车库、人防车库及配套用房。拟建建筑物±0.000 m的绝对标高为18.6/18.5 m（主楼/地下车库）；现自然地面标高为17.50～18.00 m，地形较为平坦。槽底绝对标高为8.04～15.44 m，基坑开挖深度为2.56～9.96 m。

基坑侧壁安全等级为二级和三级，基坑支护方案采用桩锚支护和挂网放坡支护型式。

已进行的主要监测项目：1）支护结构顶部水平位移、沉降；2）基坑周边地表竖向位移；3）地下水位观测；4）锚杆轴力监测；5）周边建筑物沉降监测；6）安全巡视。

监测频率：基坑开挖深度≤5 m，1次/2 d；基坑开挖深度5～10 m，1次/d。底板浇筑后时间，≤7 d，1次/2 d；7～14 d，1次/3 d；14～28 d，1次/5 d；＞28 d，1次/10 d。

监测点分布见图1。

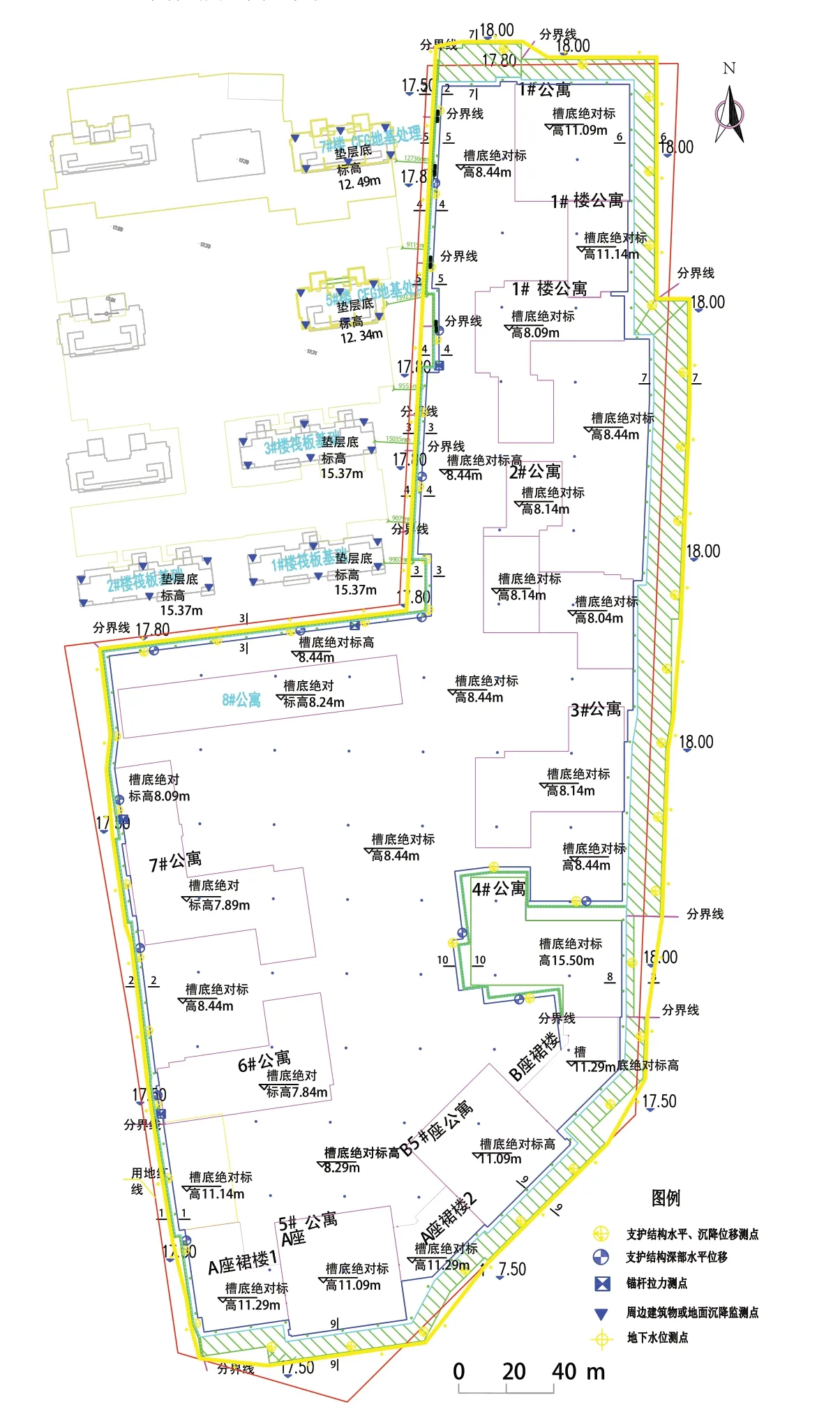
图1 监测点平面布置图Fig. 1 Location of monitoring points

2 基坑监测数据

2.1 原始监测数据的基本情况

对于已经取得的原始数据，应该从服务项目分析的角度出发，从数据的使用目的、数据的可用性、数据充足程度（是否满足分析的需要）以及数据的可靠度、数据质量的好坏做出整体的判断和评估。

就本项目而言，数据主要用于评估基坑的变形动态，基坑监测与工程施工的进度一致，数据整体的连续性、可靠性都能够得到保障，数据的精度严格按照既定的监测方案及相关规范要求执行，能够满足评估基坑安全及进行项目分析的需要。

2.2 原始监测数据产生缺失值的原因

（1）产生缺失值的原因

缺失值是指在原始数据集中，因为各种原因产生的数据空缺或丢失。数据缺失在原始监测数据集里较为常见，是在采集监测类成果或进行相关监测任务时经常遇到的问题。

监测数据缺失值的发生有很多原因，对于基坑工程，比较常见的有：1）基坑监测工作是随着作业面观测条件的完备而逐渐展开的，尤其是项目初期，存在部分点位无法监测或者暂时不具备监测条件的情况；2）实施监测任务时场地条件受限。施工现场是动态变化的，个别点位在观测时出现影响正常监测的观测障碍较为普遍；3）仪器动态监测或人工监测时出现的偶发采样数据缺失。

（2）监测数据的基础特征

监测数据的基础特征是指监测数据的一般性分类特性，数据是属于数值型变量还是离散变量，应根据数据的特点进行初步划分。

（3）与异常值的区别

异常值一般是指偏离正常值较多，且利用现有的理论或者观测状况不能给出合理解释的一类数值或某些数据。统计意义上认为良好的数据集应该是符合正态分布规律的，偏离过大的数据就存在异常的可能。

异常值是客观存在于所取得的数据集中的实际量，与缺失值有本质区别。本文主要讨论监测数据缺失值的填补，暂不对异常值的辨识和处理进行探讨。

2.3 监测数据缺失值处理的一般流程

原始监测数据缺失值处理所面临的首要问题是缺失值的识别和分类。

主要包括识别不同字段的缺失值分布状态，比如缺失值的占比、缺失值出现位置等基本情况，然后根据初判结果分别进行处理。

如果缺失值较多，单一分类内缺失值占比较高，且对整体的数据分布不产生显著的影响，考虑直接删除。但此类情况需要谨慎使用，有条件的需要做多模型对比试验分析，以确定缺失值直接删除的合理区间（陈志江等，2021）。

如果缺失值较少，单一分类内缺失值占比较低，对整体数据的影响不能忽略，则需要进行填补，可以考虑采用均值、插值等多种方式进行操作。

3 随机森林算法填充数据缺失值

3.1 算法概述

随机森林也被称作随机决策森林，它是用于分类、回归和其他类似任务的集成学习方法。它经常被用作“黑盒子”模型，因为它们可以在广泛的数据范围内生成合理的预测，而只需要很少的配置（马源等，2017）。

该算法是通过在模型训练时构造多个决策树，并输出分类结果，即单个树的分类或均值预测（回归模式下）。它的基本单元是决策树，而它的本质属于机器学习的集成学习分支。随机决策可以纠正普通决策树过度拟合的训练集合，且性能通常优于普通决策树（石礼娟等，2017）。

3.2 算法流程

以分类问题为例，首先根据分析数据集，使用自助法进行采样，生成n个训练集。n个训练集可以训练n个决策树，故决策树不必进行修剪，可以保留全部数据集特征进行训练。

每个训练集具有独立分类器（即单独的分类树），利用其进行分类。每个独立分类器根据不同的分类指标进行分类决策，决策的形式是分类器内部进行投票。最终的结果汇总成为随机森林的输入结果，要依据各分类器投票情况来确定，获得票数最多的类别就是森林的分类结果。由于每个分类器都是独立的，99.9%不相关的分类器做出的预测结果涵盖所有的情况，且互斥的分类结果会彼此抵消。将若干个弱分类器的分类结果进行投票选择，从而组成一个强分类器，少数优秀的分类器的预测结果将会做出一个好的预测。

对于数据预测，一般是根据分类过程中构造的回归树进行决策的同时，采用待填充数据集的均值或者中位值作为预设值，使用全部数据构建模型，构建过程中记录每组数据在决策树中每一分支的分类路径，搜索出与缺失值最为接近的路径。路径的长短表征了已知数据与待预测数据之间的相似程度，再根据相似度和权重大小进行填补。

3.3 待填充数据基本情况

以基坑（H7—H58）号点桩顶竖向位移变化量为例，选取的监测周期为2019年6月11日—2020年2月18日。

从H7—H58号点缺失值基本情况统计表（表1）和分布图（图 2）上看，H30—H32点缺失值的分布不集中，但占比高（27%～43.2%），这些样本在数据分析时会被直接忽略，本次填充不涉及。其他数据列存在的缺失值均小于2.7%。缺失值占比略高，不影响整体数据分布，均可以进行填充处理。H50—H58号点数据完整，无缺失。

图2 H7-H58号点桩顶竖向位移缺失值可视化Fig.2 Missing value of vertical displacement visualization at h7-h58

表1 H7—H58号点桩顶竖向位移数据缺失情况统计表Tab. 1 Missing data of vertical top displacement of pile for H7-H58

从H7、H8、H9、H49点桩顶竖向位移监测数据（图3）可见，H7、H8、H9、H49点曲线上都存在间断。

图3 H7、H8、H9、H49点桩顶竖向位移原始数据散点图Fig. 3 Basic vertical displacement data of H7, H8, H9 and H49

H7间断（空缺）最为明显，产生原因就是缺失值的存在（表2）

表2 H7、H8、H9、H49点存在缺失值的行统计表Tab. 2 Lines with missing values at H7, H8, H9 and H49

H7、H8、H9、H49点的数据统计分析结果见表3。

表3 H7、 H8、H9、H49号点桩顶竖向位移数据统计表Tab. 3 Statistics of vertical displacement of pile for H7, H8, H9, H49

3.4 填充结果

R语言的MICE包提供了多种缺失值填充的方法，并对填充模式及方法做了封装，便于实际工程调用。其可选模块中可添加RandomForest包，利用随机森林算法解决分类和回归问题（米霖，2020），直接利用前处理后数据对该模型进行缺失值填补。

根据填充结果（图 4）可见，边界处的数据填除H8号点外基本符合基坑变形的实际状态，且对边界处的填补效果较好。数据列内的填补结果除个别点位突出后，与周边数据相关性较强。在填充后的曲线图形上，还可以看到填补后数据分类性质明显，具有明显的归类特征，符合决策树算法的归类决策特点。

图4 H7、H8、H9、H49点桩顶竖向位移缺失值随机森林填充Fig. 4 Filling vertical displacement for missing values by random forest at H7, H8, H9 and H49

4 与其他填充方法的对比

缺失值数据集通常也可以采用均值、插值、回归等多种方式进行填充（王爱国等，2016）。

4.1 均值、中位数填充

以H7、H8、H9、H49点为例，桩顶竖向位移监测数据填充结果见图5。

均值填充是以控制所在列的空值以外数据的平均值进行填充，以平均值填充后结果见图5a。可以看到，对缺失值用平均值进行了填充，但对于H7、H8、H9号点2019年6月11日监测数据的填充，初始值为0的情况下，0值之前点位填充平均值不符合实际。在中部连续出现的缺失，直接利用平均值填充，未考虑数据变化趋势，其点位偏离较为明显，也不尽合理。

同理，采用中位数填充（图5b）结果与采用平均值填充情况类似。

4.2 KNN填充

KNN法（K- Nearest Neighbor法，即K最邻近法）是以待求测点周围若干已知测点值c1,c2, ...,ci为基准，来估计某其他时刻目标点测量值cx的填充方法，本质上也是一种考虑权重的插值填充方法。

其中，权重ω与距离d（邻点与目标点）成反比，即ω=1/d，n为已知测点的个数。

从填充结果（图5c）看，待填充值在两侧的数据取值区间以内，与均值法相比，填充后曲线较为平滑，没有出现明显的数据偏离，与基坑变形动态情况基本相符。

图5 H7、H8、H9、H49点桩顶竖向位移监测数据填充结果Fig.5 vertical displacement 7 filled curves of H7, H8, H9 and H49

4.3 回归分析结果填充

回归分析假定目标（待预测值作为因变量）和预测依据（已知观测数据作为自变量）之间存在一定的因果关系，利用该假设进行结果预测。一般适用于待预测值和已知观测数据存在显著关系的情况。回归分析也能够显示出待预测值和已知观测数据之间的关联强度。

利用本次选取的数据集，缺失值列作为因变量，选取了多列不包含缺失值的列作为已知观测数据，进行回归分析，选取H11—H44号点中的完整数据集作为模型输入，相关性分析结果见表4。

表4 H11—H44号点桩顶竖向位移数据相关性分析表Tab. 4 Correlation analysis of vertical displacement data of pile

通过分析结果可见，假定值出现的概率均大于0.05，说明采用回归分析的已知数据集与待填补值之间的关联程度低，不能支持数据间具有因果关系的假设，不适用于已知数据集与待填补值之间回归模型的建立。

验证该结果进行缺失值填补（图5d）可见，边界处填充值为负值，小于初始值，与实际变形情况不符。中间缺失数据填充主要依据缺失值出现区间两侧的数值，不能够很好反映整体的变形规律，在曲线上显示局部偏离严重，后期分析使用时可能会造成局部误差过大。填补结果都不理想，回归分析填充方式不适用于本数据集。

5 结论

（1）基于随机森林算法的填充方式能够判断各分类的重要程度，优选出强影响因素，结合权重进行填充，填充结果较为理想。

（2）随机森林没有对数据集各特征参数进行降维或压缩，可以适应大数据集、多特征的要求，最终采用投票的结果，可以最大限度地体现关键特征对模型的影响。

（3）随机森林作为一种集成算法，不用单独构造测试集，可以依托数据集自动提取测试集，极大地简化工作量，且能够内部进行对比、评估。

（4）为了达到合理的填充结果，在填充操作前需要进行必要的填充方式判断，确定填充范围后，还需要了解数据的基本统计特征。

监测数据的处理作为基坑变形位移规律分析的重要前置环节，不容忽视。应该根据基坑工程的实际变形特征或趋势，根据分析处理阶段的不同，合理优选适宜的数据处理方式，才能够更好地利用现场实测数据，让数据更为全面、完整地提供给模型分析，更有助于实现科学、有效的分析判断。