L波段雷达高度差报警阈值的研究与建议

沈 晔，徐志刚，马玮骏

(1.95871部队探空教研室，衡阳 421001；2.南京金水尚阳信息技术有限公司，南京 210046)

0 引言

高空气象探测雷达在探测过程中，可以得到探空仪上升过程中的实时高度，该高度一方面代表气象要素值所在高度，另一方面作为气球升速、风向风速、气球下沉段、球炸时间等的计算参数或参考指标，因此高空气象探测雷达所探测高度的准确性直接影响高空气象探测资料的质量[1，2]。

就L波段雷达综合探测而言，每秒可以得到两个高度值：一是利用探空仪所采集的温度、气压、湿度数据，通过压高公式计算出高度值，简称气压高度；二是基于雷达所测仰角和距离数据，通过三角函数计算1个高度值，简称雷达高度[3，4]。气压高度与雷达高度本质上都是指探空仪所在高度，然而由于机械误差、传感器误差、计算公式误差等的存在，这两个高度与探空仪所在高度的真值存在误差。业务探测过程中，为了评价这两个高度与探空仪高度真值的逼近程度，引入了高度差值的概念[5，6]。

当前高空气象探测业务中，理论上在雷达出现大仰角时，会出现高度差报警阈值过大，失去报警意义；实际探测中，高度差报警阈值在探测中期会出现极大值，即高度差报警阈值并不随探测高度而单调变化。针对该问题，文章分析了高空气象探测中雷达高度、气压高度以及两者之间的异同，其次说明了雷达高度差值的来源，并深入探讨了高度差值报警的原理，结合实际探测业务分析了高度差报警阈值的应用案例，最后给出了L波段雷达高度差值报警的改进建议。

1 相关定义

1.1 雷达高度

已知地面雷达海拔高度、探空仪与地面雷达的距离(又称斜距)以及探空仪相对于地面雷达的仰角，通过三角函数可以计算出探空仪距地面雷达所在平面的垂直高度，从而得到探空仪的海拔高度，即通过雷达测量探空仪的海拔高度，简称雷达高度。

取极坐标系，如图1所示，O表示雷达天线(即测站)所在位置，A为探空仪在某一时刻的空间位置，C为探空仪所在空中位置P的水平投影点，δ为OA与OC的夹角，R为探空仪所在空中位置A距测站O的直线距离(即斜距)，ON为正北方向，那么探空仪距测站的垂直高度Z表示为：

Z=R·sinδ

(1)

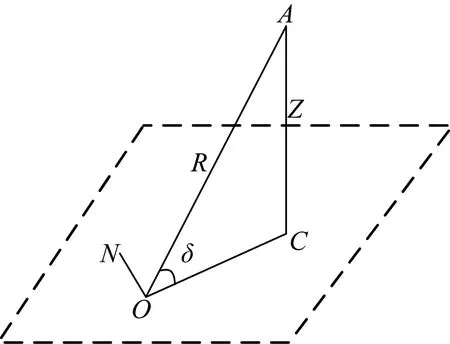
图1 雷达高度示意图

假设测站海拔高度为Ho，那么探空仪的海拔高度HA表示为：

HA=Ho+Z=Ho+R·sinδ

(2)

由公式(2)可知，探空仪的海拔高度HA是通过雷达所测得仰角δ、斜距R、测站的海拔高度Ho计算得到，因此HA也称为探空仪的雷达高度。

公式(2)仅是计算雷达高度的核心公式，在实际应用过程中，需要注意的是：

1)由于大气折射率的存在，公式(2)中的雷达所测仰角δ与斜距R，均应该进行大气折射修正；

2)雷达所测斜距R，其量值是几何长度的“米”，在提供给天气学和气候学时，需要转换为与测站重力加速度相关的位势高度；

3)探空仪雷达高度是基于雷达天线旋转中心所在站心坐标平面的，在计算探空仪位势高度时，需要将其转换成地心坐标上。

1.2 气压高度

根据《常规高空气象观测业务规范》中计算位势高度的公式(即“气压-高度公式”，也简称“压高公式”)，可以计算出各相邻两气压层之间的厚度，将逐层厚度累计，得到的累计厚度，即气压高度，计算公式如式(3)所示：

(3)

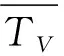
由公式(3)可知，探空仪的气压高度是通过计算逐层厚度(通常前后两组探空数据的厚度为一层)，然后将逐层厚度累加而得，因此在使用过程中需要注意以下几点：

1)同一位置探空仪，由于探空数据异常、删除等原因，其气压高度可能存在较小偏差；

2)探空仪测得的温度、湿度也是计算气压高度的因子，但对气压高度的数值影响较小。

1.3 雷达高度与气压高度的异同

1)相同点

①雷达高度和气压高度均可以表征探空仪与地面之间的距离；

②雷达高度和气压高度均是通过公式间接计算而来，不是直接测量值；

③雷达高度和气压高度不一定等于探空仪高度的真值。

2)差异点

①雷达高度是通过几何公式计算得出，单位：m；而气压高度是基于大气静力学方程推导而来，其单位是位势米，因此两者需要统一量纲后才能对比。

②雷达高度的准确度取决于雷达所测探空仪的方位角、仰角以及雷达与探空仪之间斜距是否准确；而气压高度的准确度取决于探空仪所测得的气压、温度和湿度是否准确。

2 高度差值

2.1 高度差值定义

如图2所示，假设O为雷达天线所在位置，其海平面高度为Ho，某一时刻，雷达所测探空仪的雷达高度的位置为A，气压高度位置为B，A、B在水平面上的投影均为C(实际上，空间位置B在水平面上的投影不一定是C，为了便于描述，在保持B高度不变的情况下，将B水平位移到C的垂直上方)，此时斜距|AO|为R(R≥0)，雷达仰角∠AOC为α(0≤α≤90°)，气压高度位置的仰角∠BOC为β(0≤β≤90°)，两者之间的角度差∠BOA的值为γ，其计算公式如下：

(4)

而高度差值的计算公式为：

(5)

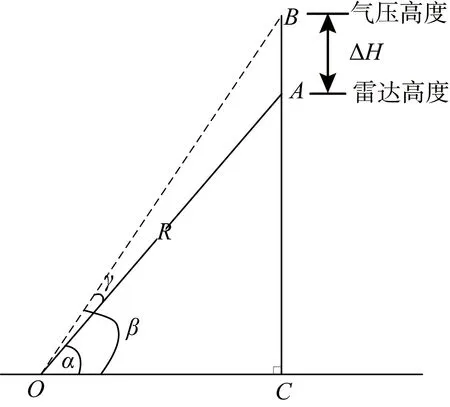
图2 雷达高度差值示意图

2.2 高度差报警原理

高空气象探测业务所述雷达高度差大，即公式(5)中ΔH的绝对值大于阈值ΔHmax(ΔHmax>0)，导致放球软件高度差报警[7]。然而，目前高空气象探测雷达终端软件判断雷达高度差大小是根据夹角γ来判断的：当|γ|≤1°时，判断为雷达高度差值正常，终端软件显示雷达高度差不报警，而当|γ|>1°时，则认为雷达高度差过大，终端软件显示雷达高度差报警。

然而实际工作中，探测人员对γ的阈值并不敏感，也不直观，因此文章对公式(5)做进一步推导：

(6)

分析公式(6)可知，在高度差值不报警的前提下，当γ取极值-1°或1°时，雷达高度差值ΔH的绝对值也取极值ΔHmax，ΔHmax只与斜距L、仰角α有关，换而言之，报警阈值ΔHmax是一个变量。

为了直观表示ΔHmax的变化情况，分别给出γ=1°和γ=-1°时，报警阈值ΔHmax随斜距L、仰角α的变化关系如下：

1)当γ=1°，高度差值ΔH的极值随着仰角α的增大而增大；

2)当γ=-1°，高度差值ΔH的极值随着仰角α的增大而减小；

3)随着仰角α的增大，高度差值ΔH极值增大或减小的幅度越来越大。

特别地，当仰角α≥70°时，报警阈值ΔHmax变化特别大，甚至达到了2000 m以上，报警阈值ΔHmax越大表明高度差值报警条件越宽松，就实际工作而言，以该报警阈值(如大于2000 m)作为判断雷达高差过大的标准，若ΔHmax过大，则失去了高度差报警的目的。

3 报警阈值应用分析

3.1 资料来源

文章选取邵东气象台不同季节的4份探空资料球坐标数据，分析报警阈值在实际应用过程中的变化规律，所选取的探空资料已经通过了质量控制，且终止原因均为球体破裂，4份资料的具体信息如表1所示。

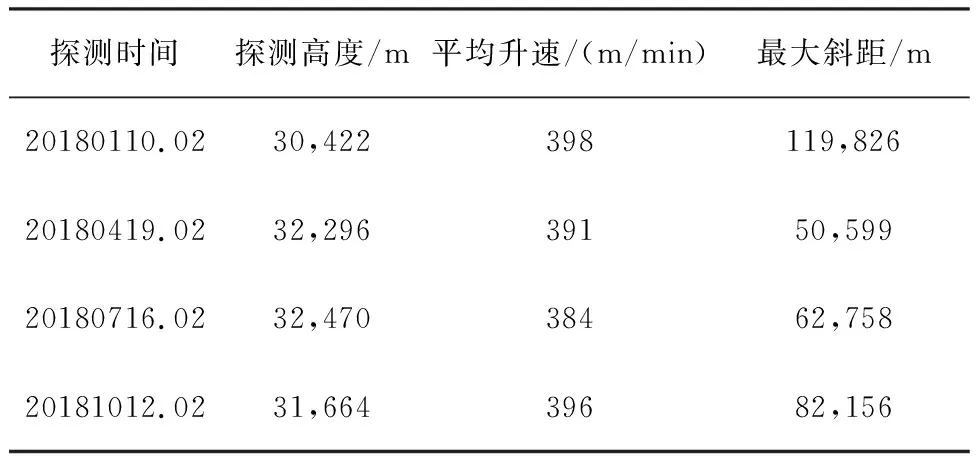
表1 邵东气象台所选资料信息

3.2 应用分析

基于表1的4份探测资料，分别计算在探空仪上升过程中的实际仰角、斜距，绘制出高度差报警阈值的变化情况。

通过分析4份资料的报警阈值可知：

1)在整个探测过程中，报警阈值总体呈倒三角形。

2)施放时间越长，探空仪高度越高，报警阈值也越大。这主要是由于高空雷达保持了一个较小的仰角，报警阈值主要随斜距的增大而逐渐增大。

3)在斜距变化不是特别大的时候，随着仰角出现先增大后减小的变化趋势，报警阈值也出现先增大后减小的变化趋势。

综上，具体探测业务中，在探空仪上升过程中目前L波段雷达终端软件的报警阈值并不是单调变化的，而是与实际的仰角和斜距有关。

4 结束语

4.1 报警阈值存在的问题

在高空气象探测业务中引入高度差，其目的是通过计算两个高度的非真值(即雷达高度和气压高度)之间的逼近度，间接证明雷达高度和气压高度的可信度，以确保探空仪高度测量的准确性，然而由于间接计算高度无法避免测量误差，且当前气象资料使用者(气象预报员或保障决策者等)只需要得到符合气象保障任务的高度准确度值即可，是允许高度存在一定程度的误差，因此如何将“一定程度的误差”进行量化，需要进一步探讨。

当前L波段雷达终端软件是通过约束公式(4)中夹角γ的范围来确保高度测量的准确性，这种方法存在以下3方面问题：

1)理论上，高仰角(如大于70°)时的高度差报警阈值会很大(如大于2000 m)，从而失去报警意义；

2)在实际探测业务中，报警阈值在探测中期会出现极大值，并不随探空仪高度增大而单调变化；

3)当前高度差报警阈值的设置依据是基于气压敏感元件和雷达装备自身的测量误差而得，不是根据气象资料使用者的允许误差而得，因此这种方法得出的高度差报警阈值与气象资料使用者能接受的高度差允许阈值不同，从资料应用角度而言，也就不具备参考性。

4.2 建议

《常规高空气象观测业务规范》中明确“0～20 min，每1 min为1个计算层风，20～40 min，每隔2 min为1个计算层风，40 min以上，每隔4 min为1个计算层风”，可得出不同施放时间段内计算层风的厚度是不相同的；进一步，在相同的可信度下，计算层风的厚度愈大，表明其可“容忍”的高度偏差也愈大。因此，下一步可以根据不同施放时间段，设置不同的报警阈值，这样从高度差值的应用角度而言更符合实际需求[8]。