基于滑模控制的PMSM直接转矩控制研究＊

林立，刘凡

（1.多电源地区电网运行与控制湖南省重点实验室，湖南 邵阳 422000；2.邵阳学院电气工程学院，湖南 邵阳 422000）

永磁同步电机（PMSM）为一种高性能的伺服控制电机，其特征表现为适用性强、结构简单、损耗小。近年来在市场需求的推动下，永磁同步电机的性能水平日益提升，且在智能控制、航空领域都获得了应用［1-2］。但是这种电机在控制时涉及到多变量、变参数，因而控制难度较高。

在传统的DTC过程中，关键的控制对象是磁链和转矩，其优势表现为实时性高，可高效地抵抗环境干扰［3］。直接转矩控制过程中，先确定出定子电压和电流的相关参数，然后在电压矢量基础上实现直接控制目的。但受到开关频率因素的影响，其电压矢量的有效值和期望值存在较大偏差，导致DTC中磁链和转矩出现明显的波动，影响了总体性能［4］。

在研究过程中为提高开关频率稳定性，对这种电机进行控制时，引入SVPWM调制技术［5-6］。进行简化后应用滑模控制(sliding mode control，SMC)算法，对此算法的性能进行仿真研究，结果发现其控制精度高，有较高的抗噪性，表现出良好的应用价值。控制算法决定了控制器的性能，为验证永磁同步电机控制策略的有效性，必须进行实验验证［7］。

1 PMSM数学模型

在研究PMSM时，考虑到数学分析要求，进行了下面假设：a.该电流是对称的三相正弦波电流；b.涡流和磁滞损耗可以忽略不计；c.不包括铁芯的饱和效应。

根据理论分析可知，在旋转d-q系下，PMSM电机的控制模型表达式为：

公式里：ud、uq、id、iq、ψd、ψq、Ld、Lq依次对应定子电压、电流、磁链及电感的d-q轴分量；R是定子电阻；ωe是电角速度；ψf对应永磁体磁链。

上述表达式表示内置式三相PMSM电机的数学模型，对于表贴式三相PMSM，可令Ld-Lq=0。

2 直接转矩控制器的设计

同步旋转坐标系d-q下，通过表面安装三相PMSM求解电磁转矩Te的公式如下：

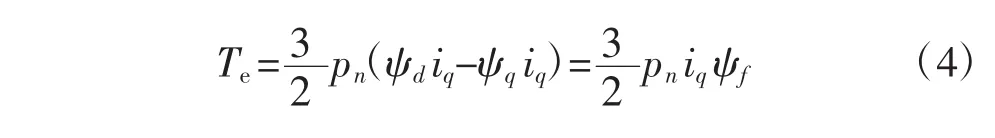
定子磁链矢量的方向与d轴方向相同时，ψr=ψd，定子磁链幅值可表示为

在滑模控制算法中，对动态系统而言，其数学模型可描述为：

式中：n表示输入变量；a（x，t）、b（x，t）、g（x，t）对应于未知函数。

以下表达式对应于模型中的滑动变量函数与导函数：

式中ST对应转矩的滑模面函数。

令r=0.5，下图1具体表示这种优化的DTC控制模型框图。

图1 基于滑模控制的DTC框图

3 系统建模仿真与结果分析

3.1 仿真模型的搭建

该控制模型建立后，该滑模控制系统的性能通过Matlab仿真分析得到验证，为实际应用提供支持。其系统框图如图2所示。

图2 基于滑模控制的永磁同步电机DTC框图

下图3显示出这种系统的模型，表1为电机的参数，进行仿真时根据实验相关要求，而设置开关频率为5kHz，持续0.4s。

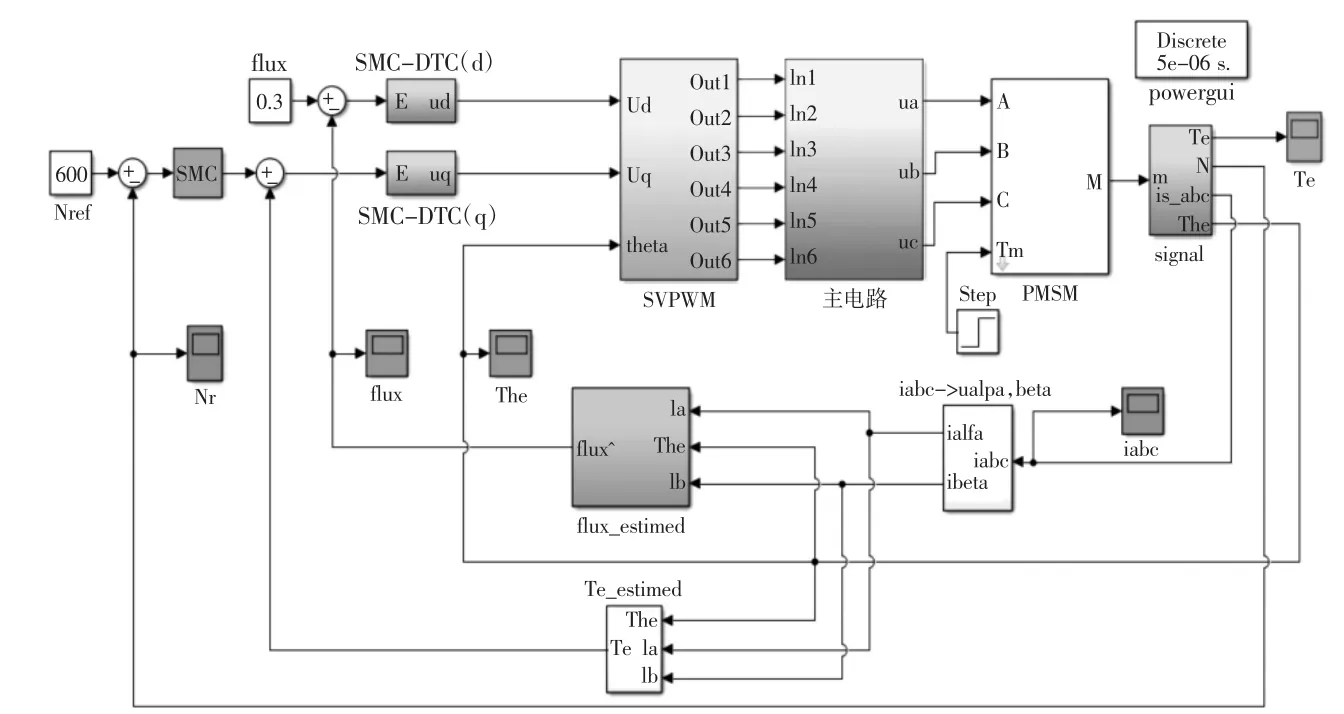
图3 基于滑模控制的永磁同步电机DTC系统仿真模型

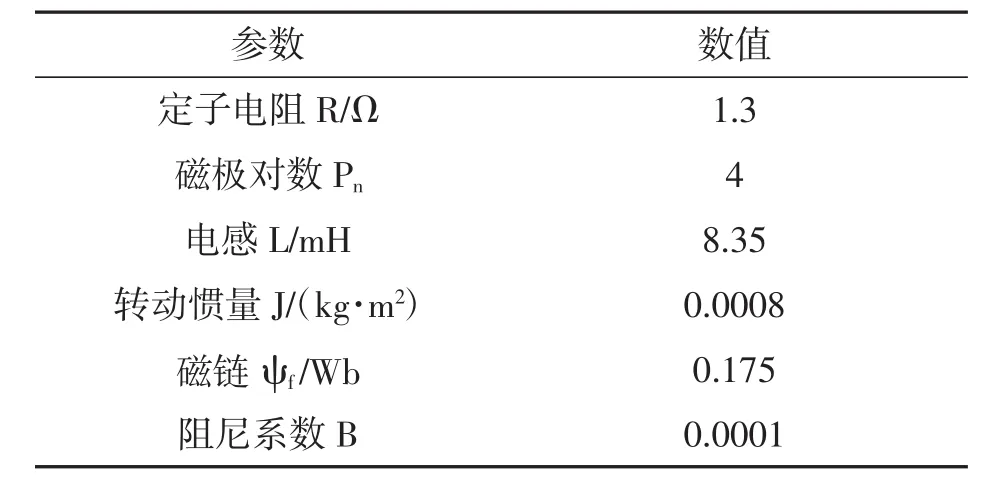
表1 PMSM的参数

3.2 仿真结果与分析

对比分析是在PMSM控制过程中，对传统DTC和基于滑模控制的DTC算法的性能，在以上参数条件下进行仿真，所得结果如图4～6。在定子磁链为0.3Wb恒定，参考转速给定Nr=600r/min，0.2s时突加加载1.5N·m的情况下，根据图4(a)和(b)我们可知，对比传统直接转矩控制系统的速度波形和优化控制系统的速度波形，与传统直接转矩控制系统的速度波形相比，控制系统的优化最初看起来仍是有超调的，但其动态响应速度高，转速观测值更稳定。传统的直接转矩控制的调整时间为0.016s，而优化的控制系统的调整时间为0.005385s。如果0.2s突然加载，传统的DTC算法不能还原到期望的转速，而基于滑模控制的DTC控制系统能快速恢复到给定参考值，表明系统的抗干扰性有所增强。

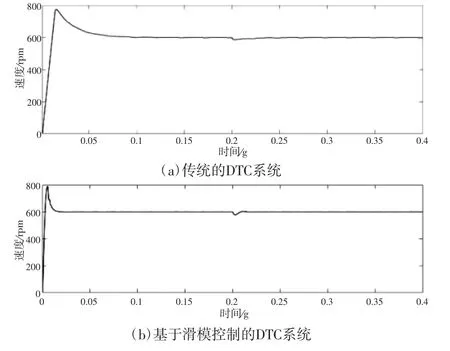
图4 系统转速波形

根据图5我们可知，选择“［0.25s，0.27s］”进行观测的时候，传统的直接转矩变动范围为0.508N·m至2.216N·m，转矩变动范围为1.708N·m，优化后的系统转矩变动范围为1.050N·m至2.150N·m，转矩变动范围为1.1N·m，转矩变动区间显著减小，因而改善了输入性能。

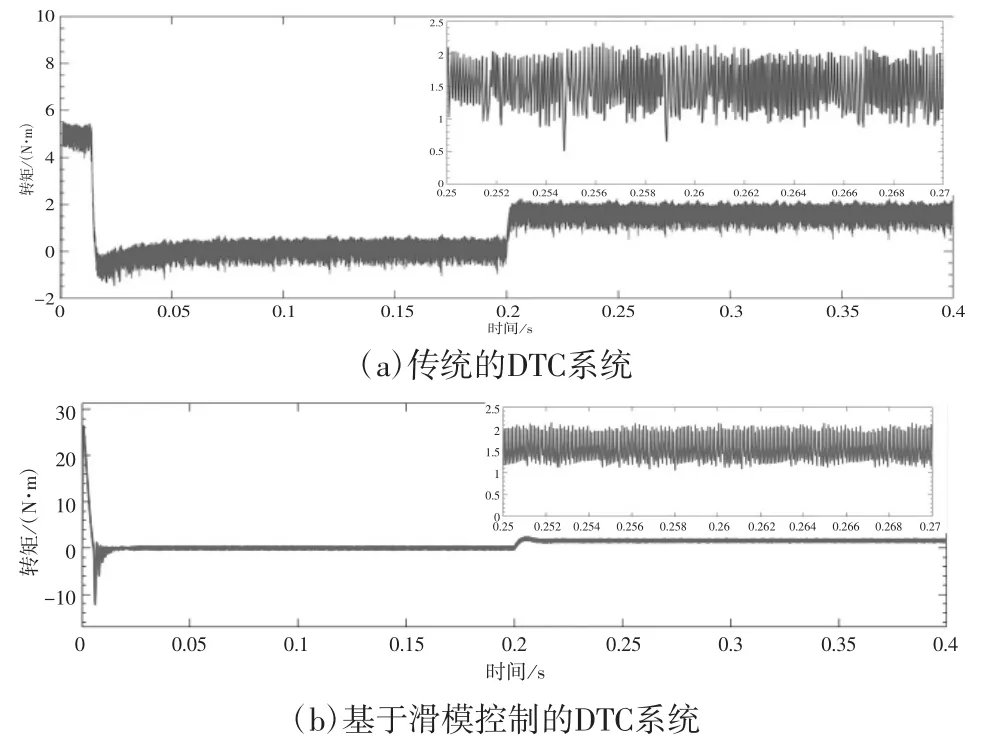
图5 系统电磁转矩波形

根据图6我们可知，传统DTC系统的磁链波动范围为0.2922Wb至0.3054Wb，磁链脉动为0.0132Wb，而优化后系统的磁链波动范围为0.2954Wb至0.3066Wb，磁链脉动为0.0112Wb，可以看出，磁链的波动区间显著缩小，从而明显减少电机抖动噪声。

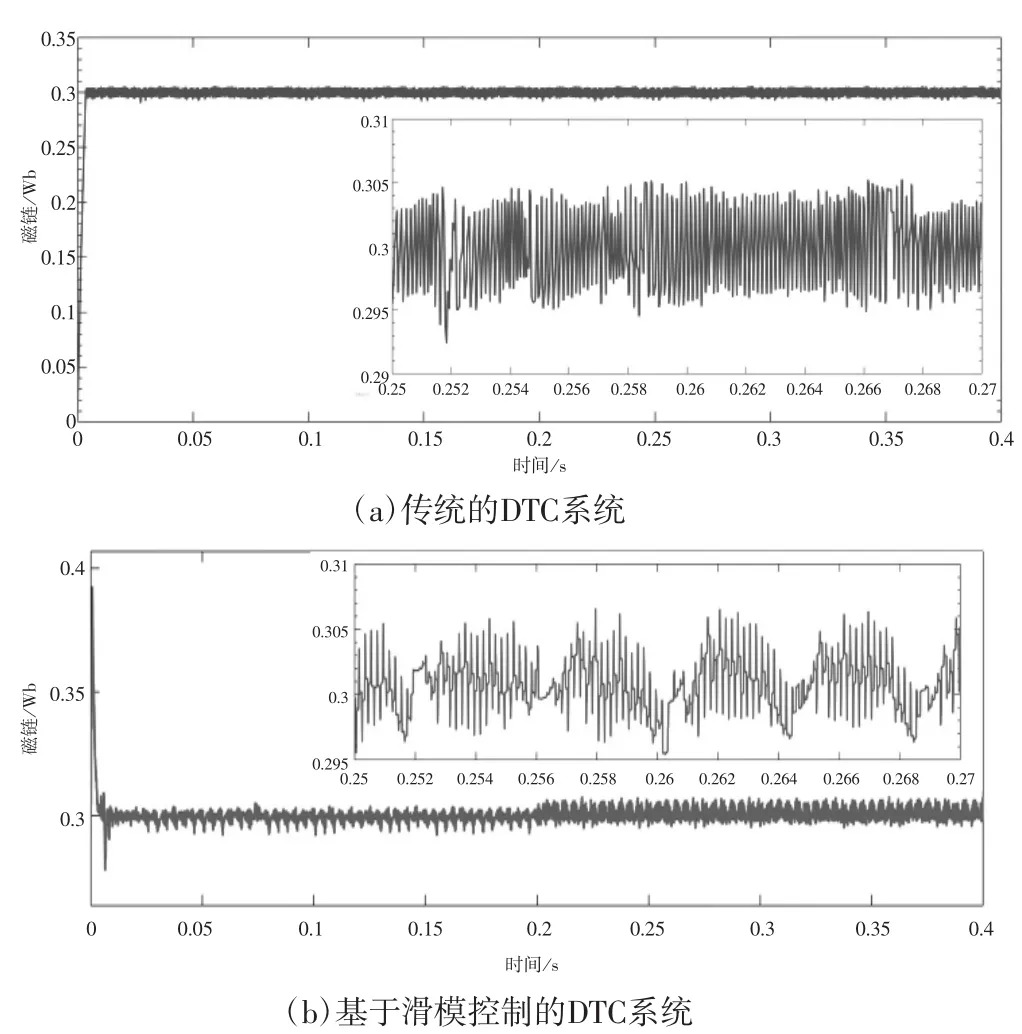
图6 系统磁链波形

对比分析以上的仿真曲线结果可知，和优化的控制模型相比，传统控制模型的响应时间长，且出现明显的抖振；而优化模型的响应时间短，出现的抖振不明显，抗噪性强，系统的鲁棒性能也明显提高。

4 实验验证

4.1 实验平台设计

在构建实验平台时，选用TMS 3200 F 28335芯片作为处理器。实验结构由控制电路、电源和PMSM组成。其中，控制电路的组成单元为此芯片和相应外围电路。电力电路包括驱动放大电路、IGBT功率开关管以及其他检测电路。可参照图7。

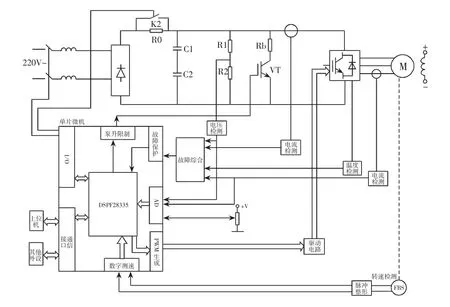
图7 PMSM的DTC系统实验平台整体结构示意图

其中功率模块实验板为自主研制，在Altium Designer模块中进行绘图，建立起PCB图，经制板、焊接、调试而成。下图8显示出对应的实物图。图中1-220V开关电源；2-15V开关电源；3-空气开关；4-DSP;5-仿真器；6-功率模块实验板；7-保险丝。

图8 PMSM的DTC系统实验平台实物图

4.2 试验结果与分析

对本文研究的基于滑模控制的直接转矩控制系统进行试验验证，试验条件和参数设置情况都和仿真保持一致。图9所示为基于滑模控制的直接转矩控制系统的稳态实验结果。试验中系统初始启动实际上有摩擦力，故初始转矩有0.5N·m左右的大小。

图9 基于滑模控制的DTC系统的稳态试验结果

如表2所示，显示出稳态情况下各参数的波动大小。以更直观地表现基于滑模控制的DTC系统控制电磁转矩、转速及定子磁链的稳定性及准确性。

表2 参数的波动大小

表2中数据说明，定子磁链在两种工况下其波动值均为±0.01Wb，转速波动值最大为±27r/min，电磁转矩的波动值最大为±0.2N·m，。其结果表明基于滑模控制的直接转矩控制系统鲁棒性好，响应速度快。根据以上实验结果可知，该控制系统具有转速和转矩小的振动和高的响应速度，且表现出良好的稳定性，突变负载对其不会产生明显影响，因而其总体控制性能良好，可满足实际应用要求。

5 结论

本文针对基于滑模控制的直接转矩控制系统进行研究，在控制过程中利用SVPWM技术替代滞环控制，从而得到稳定性高的电压矢量信号，以便提高开关频率稳定性。在磁链和转矩控制中，此种模型的鲁棒性好，可预防环境因素的干扰，稳定性高。仿真研究表明，传统DTC系统的调节时间、转矩和磁链脉动都逊色于基于滑模的DTC系统，后者能够更好地消除抖动，系统的抗干扰性能明显提高。试验结果表明：基于滑模控制的直接转矩控制系统能保持良好的稳态性能和快速的动态响应。