耦合失稳模式与控制策略综合验证技术

石 伟, 张 静, 郑宏涛, 蔡巧言, 李贵成

(中国运载火箭技术研究院, 北京 100076)

引 言

随着航天技术的发展, 航天飞行器逐渐从以运载火箭、 载人飞船等为代表的轴对称布局向以航天飞机为代表的面对称布局演变. 采用面对称布局的航天飞行器升阻比更大, 可实现更宽速域、 更大空域的飞行, 是目前航天领域的研究热点. 然而, 此类航天飞行器面临着复杂的耦合稳定性[1]和可控性问题[2], 与传统轴对称布局飞行器和低空低速飞行器相比, 易出现偏离、 振荡和发散等失稳现象. 美国X-2、 X-15等面对称飞行器发生的飞行事故也表明, 耦合特性对飞行器总体性能的影响不可忽略, 而对这些现象及其背后机理认识的欠缺严重阻碍了飞行器性能的提升.

鉴于此, 在新型航天飞行器的研发过程中, 飞行器耦合特性研究、 飞行性能及品质的预示评估成为非常重要的一个环节. 传统的飞行性能预示方法主要是基于小攻角、 小扰动线性假设, 根据飞行器的各气动系数和气动导数进行飞行力学仿真和分析, 获取飞行稳定性与可控性. 传统方法局限于线性范围内, 对大攻角等非线性情况不再适用, 同时设计中所涉及的一些基本导数也较难确定, 不具有对非线性范围内飞行性能和品质的预示能力.

为适应新型航天飞行器的研制需求, 应探索新技术, 如数值虚拟飞行、 风洞虚拟飞行等, 挖掘飞行器非线性范围内的稳定性和可控性, 给出飞行器的飞行动力学和控制系统的综合品质, 支撑飞行性能评估. 通过综合传统研究手段和新技术, 研究新型航天飞行器的运动稳定性及可控性, 将加深对耦合效应的认识, 验证耦合特性和利用耦合的正确性和有效性, 进而指导先进飞行器设计.

1 航天飞行器横航向耦合问题

新型航天飞行器以面对称布局为特征, 飞行速域宽、 空域大, 典型飞行剖面如图1所示， 图中横轴为飞行速度， 纵轴为飞行高度.

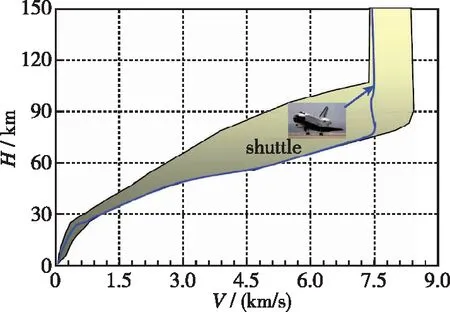
图1 新型航天飞行器飞行剖面Fig. 1 Flight profile of new aerospace vehicle

图2 典型面对称航天飞行器航向稳定性Fig. 2 Directional stability of typical planesymmetric aerospace vehicle

(a) Axis-symmetric vehicle

由于复杂的多源耦合, 飞行器偏航、 滚转通道产生强烈相互作用, 如图3所示， 纵坐标k表示其他通道产生的偏航干扰力矩与偏航通道的偏航控制力矩之比， 可见， 面对称飞行器耦合影响比类轴对称飞行器大至少一个数量级， 通道间耦合影响远大于偏航通道控制能力， 这将对飞行稳定性造成严重影响.

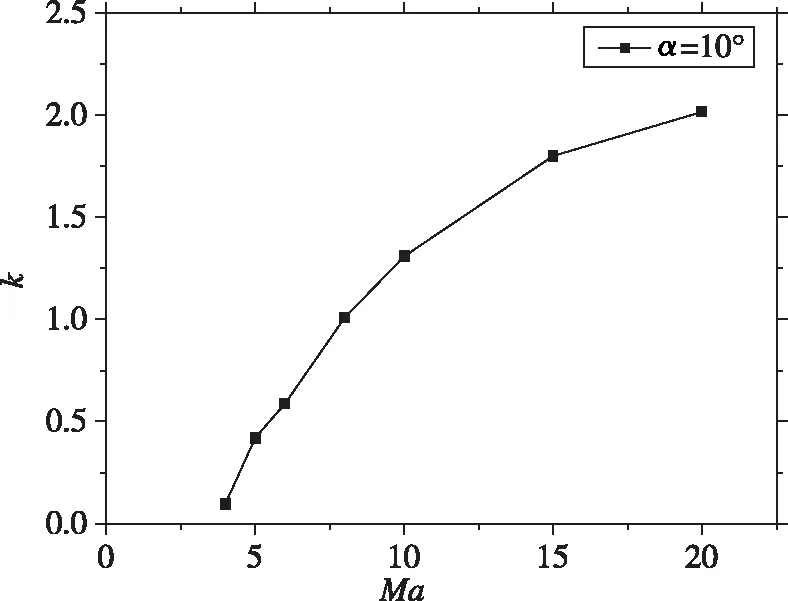
(b) Plane-symmetric vehicle图3 其他通道耦合作用与偏航通道控制能力对比Fig. 3 Comparison between coupling effect of other channels and controll ability of yaw channel

此外, 偏航通道转动惯量比滚转通道转动惯量至少大1个数量级, 偏航通道的小量控制会激发滚转通道的较大响应, 容易使飞行器快速发散. 复杂的绕流流场、 大跨度的速域空域环境使得面对称航天飞行器的稳定性和可控性恶化, 气动、 运动、 惯性等多种耦合同时出现, 导致横航向耦合效应更加严重.

传统轴对称飞行器的流场结构相对简单, 耦合特性对于飞行器总体性能的影响处于可忽略的量级, 通常采用解耦设计即可满足总体性能指标要求. 而对于面对称航天飞行器, 气动设计追求高升阻比, 气动外形趋于扁平化; 若按照解耦设计理念, 需要适当增加静稳定度以确保整个飞行区间的稳定性, 这势必造成升阻比、 机动能力的大幅下降; 加之飞行器的流场结构更复杂, 通道间耦合更严重, 各种干扰和不确定性影响不能简单地忽略, 传统设计方法难以满足设计需求.

新型航天飞行器复杂的横航向耦合问题严重影响了飞行器总体性能的提高, 为此需深入研究流场结构和耦合效应, 揭示耦合机理, 发展新型考虑耦合效应的控制方法.

2 耦合失稳模式与控制策略综合验证技术

耦合机理的揭示有助于加深对耦合问题的认识, 可指导新型控制策略研究, 但耦合失稳模式和新型控制策略的正确性只有经过全面的验证, 才能加快向工程应用推广. 基于目前的技术水平, 主要的验证手段包括仿真分析、 地面试验和飞行试验.

仿真分析包括动力学仿真分析和CFD-RBD仿真分析等. 动力学仿真主要是通过求解刚体动力学方程获得自由飞行轨迹和姿态时间历程, 仿真使用的气动力和力矩是基于CFD定常计算结果插值得到的, 此种方法得到的气动力没有考虑速度、 姿态角等因素变化引起的非定常效应. CFD-RBD是一种通过耦合求解非定常N-S方程和刚体动力学方程进行自由飞行轨迹和姿态仿真的方法, 该方法可用于预测飞行器运动过程中的非定常气动特性和飞行力学特性[3-8].

主要借助风洞和动态试验装置来实现地面试验. 风洞用于提供稳定的来流条件, 模拟飞行器飞行过程中受到的气动作用; 动态试验装置提供转动自由度或模拟飞行过程中的机动动作[9]. 风洞虚拟飞行试验进一步引入控制律, 实现飞行过程控制响应的地面模拟, 评估飞行器飞行动力学和控制系统的综合品质. 针对风洞虚拟飞行试验技术, 国内外开展了相关研究[10-16], 但主要针对轴对称导弹和航空飞行器, 试验模拟速度也以低速和亚声速为主, 缺乏针对面对称航天飞行器的高速风洞虚拟飞行试验技术的研究.

飞行试验是验证飞行器综合性能最直接、 最有效的方式, 但试验周期长、 经费需求大, 适宜在充分进行仿真分析和地面试验的基础上开展.

结合各种验证技术的优缺点和技术水平, 设计了针对耦合失稳模式和新型控制策略的综合验证方案. 动力学仿真手段灵活, 具备初始扰动下开环运动特性和引入控制策略后闭环运动特性的仿真能力, 可实现对耦合失稳模式和新型控制策略验证需求的全面覆盖. 在动力学仿真基础上, 筛选发生耦合失稳的典型状态点, 针对荷兰滚失稳模式和副翼操纵耦合失稳模式, 开展CFD-RBD仿真验证; 针对高空俯仰机动诱导滚转失稳模式, 开展强迫拉起条件下的自由滚转运动特性风洞试验验证. 对于新型控制策略, 在发展高速风洞虚拟飞行试验技术的基础上, 开展风洞虚拟飞行试验验证, 实现对耦合特性和控制策略的综合验证.

3 综合验证研究结果

通过论证综合验证方案, 对耦合失稳模式和控制策略开展了全面验证. 本文重点给出了CFD-RBD仿真验证和高速风洞虚拟飞行试验验证结果.

3.1 CFD-RBD仿真验证

以面对称外形飞行器为研究对象, 通过CFD-RBD方法验证了荷兰滚失稳和副翼操纵耦合失稳两种典型耦合失稳模式. 仿真采用给定初始扰动的开环方式, 未加入控制律, 满足受扰后无控条件下飞行姿态演化过程的研究需求, 可验证失稳模式. 气动控制方程采用可压缩RANS方程, 飞行力学控制方程采用6自由度运动方程. 气动和飞行力学的耦合求解采用了一种改进的松耦合方法, 该格式在选择合适的气动和飞行力学求解器情况下, 可达到2阶时间精度, 且计算量与松耦合格式相同.

根据耦合失稳模式验证需求, 选取的典型飞行状态为高度H=33 km, 马赫数Ma=5, 攻角α=24°.

首先对飞行器基本气动特性及失稳判据参数进行了分析. 图4给出了俯仰通道舵偏δe为5°, 10°, 15°时, 相对飞行器质心的俯仰力矩系数Cmz.由图可见, 飞行器纵向处于静不稳定状态.β=0°时, 俯仰配平舵偏约为δe=10.17°.

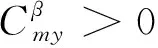
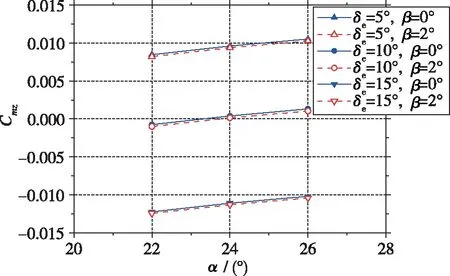
图4 不同俯仰舵偏下的俯仰力矩系数(Ma=5)Fig. 4 Pitch moment coefficient at different elevator angles(Ma=5)

图5 稳定性参数(Ma=5)Fig. 5 Stability parameters

横向操纵偏离参数LCDP主要取决于飞行器的横航向静稳定性参数和操纵导数. 对于此类飞行器, 副翼操纵一般会导致不利偏航力矩, 加之大攻角状态下飞行器航向静不稳定, 最终导致了操纵反效, 即LCDP>0.

基于以上分析, 典型飞行状态下, 飞行器航向动稳定但横向操纵反效, 即与失稳判据对应的荷兰滚失稳模式是稳定的, 而副翼操纵耦合失稳模式是不稳定的.

荷兰滚失稳模式仿真初始状态为高度H=33 km, 马赫数Ma=5, 攻角α=24°, 侧滑角β=0.1°, 俯仰通道舵偏δe=10.17°, 滚转通道舵偏δa=0°, 偏航通道舵偏δr=0°. 图6给出了通过动力学线性仿真得到的侧滑角变化历程. 由于该状态下飞行器航向动稳定, 在β=0.1°初始扰动下, 飞行器侧滑角在 -0.1°～0.1° 范围等幅振荡, 仿真结果与判据判别情况一致.

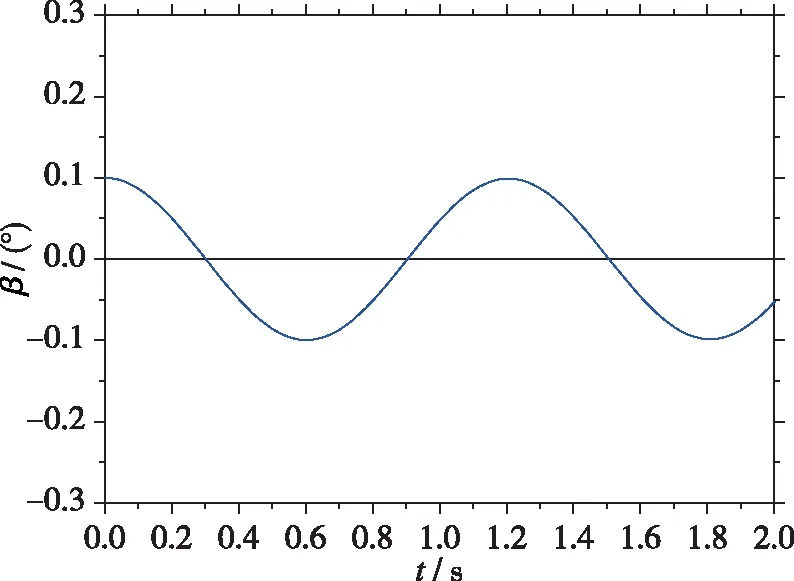
图6 荷兰滚失稳模式侧滑角动力学线性仿真结果Fig. 6 Linear dynamics analysis of sideslip angle for Dutch roll instability

图7给出了CFD-RBD仿真结果, 此时飞行器绕流流场与刚体运动耦合求解, 反映了飞行过程中飞行器在非定常气动作用下的运动特性. 图中Mx为相对飞行器质心的滚转力矩，My为相对飞行器质心的偏航力矩. 由图可见, 初始正侧滑状态下, 飞行器受到正偏航力矩和负滚转力矩的作用, 正偏航力矩将使飞行器侧滑角增大, 负滚转力矩将使飞行器侧滑角减小. 由于起稳定作用的滚转力矩比起不稳定作用的偏航力矩大, 飞行器侧滑角开始减小. 随侧滑角变化, 滚转力矩和偏航力矩也随之交替变化, 之后侧滑角逐渐衰减, 表明飞行器航向是动稳定的, CFD-RBD仿真结果与判据判别情况一致. 由于初始状态下, CFD计算得到的俯仰力矩不为0, 为较小的负值, 俯仰静不稳定导致飞行攻角不断减小, 但不影响航向动稳定.

副翼操纵耦合失稳模式仿真初始状态为高度H=33 km, 马赫数Ma=5, 攻角α=24°, 侧滑角β=0°, 俯仰通道舵偏δe=10.17°, 滚转通道舵偏δa=0.5°, 偏航通道舵偏δr=0°, 初始状态无侧滑但滚转通道舵偏 0.5°. 图8给出了滚转角γ的动力学线性仿真结果. 在初始正滚转通道舵偏作用下, 飞行器开始负向滚转, 约0.45 s时滚转角达到负向最大, 之后飞行器开始正向滚转, 约0.72 s后滚转角变正, 并持续正向增大, 飞行器出现操纵反效, 仿真结果与判据判别情况一致.

图7 荷兰滚失稳模式CFD-RBD仿真结果Fig. 7 Results of CFD-RBD for Dutch roll instability

图8 副翼操纵耦合失稳模式滚转角动力学线性仿真结果Fig. 8 Linear dynamics analysis of roll angle for lateral control instability

图9给出了CFD-RBD仿真结果. 初始正滚转舵偏产生了负滚转力矩, 使模型负向滚转, 同时导致负侧滑且幅值不断增大, 在滚转稳定性作用下, 滚转力矩开始减小并逐渐变正, 负向滚转速度逐渐减小, 滚转方向也由负向滚转逐渐变为正向滚转. 初始正滚转舵偏同时也产生了负偏航力矩, 带来不利偏航影响, 加剧了初始阶段侧滑角的负向增大. 两方面原因共同作用下, 约0.72 s后滚转角变正, 飞行器出现操纵反效, CFD-RBD仿真结果与判据判别情况一致. 由于初始状态下, CFD计算得到的俯仰力矩不为0, 为较小的负值, 俯仰静不稳定导致飞行攻角不断减小, 仿真1 s时间内, 攻角从24°减小到22.4°, 但不影响操纵反效现象.

经以上分析对比, 采用CFD-RBD方法得到的飞行器运动特性与耦合失稳判据、 动力学线性仿真结果一致, 验证了荷兰滚失稳、 副翼操纵耦合失稳两种典型失稳模式及判据的正确性.

图9 副翼操纵耦合失稳模式CFD-RBD仿真结果Fig. 9 Results of CFD-RBD for lateral control instability

3.2 高速风洞虚拟飞行试验验证

以面对称外形飞行器为研究对象, 设计并开展了高速风洞虚拟飞行试验, 验证了新型控制策略的正确性和有效性.

试验在中国航天空气动力技术研究院FD-16风洞中开展, 试验状态为Ma=5, 飞行攻角α=25°.

针对横航向耦合特性验证需求, 设计了偏航滚转两自由度支撑机构, 如图10所示, 该机构可提供偏航-滚转两通道自由度. 根据试验状态, 设计模型初始安装状态下具有25°攻角, 即模型轴线与滚转轴夹角为25°. 滚转轴始终与风洞来流方向平行, 偏航轴始终与滚转轴垂直, 模型转动中心与质心重合. 基于此两自由度支撑机构, 模型可绕滚转轴、 偏航轴自由转动, 转动过程中, 模型攻角始终保持不变, 速度滚转角、 侧滑角随模型转动而变化.

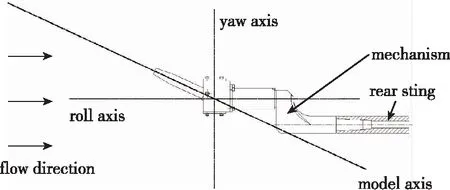
图10 支撑机构及转动轴线示意图Fig. 10 Sketch of supporting mechanism and rotation axises

基于该两自由度支撑机构, 完成了动力学建模、 飞控律开发、 飞控系统集成试验及试验系统联调测试等工作, 具备开展风洞试验的条件.

针对常规控制策略和新型控制策略, 分别开展了横航向姿态保持试验和横航向机动控制试验, 姿态保持试验的滚转角指令一直保持在0°, 机动控制试验的滚转角指令变化过程为0°→-5°→0°.

对于姿态保持试验, 在基本相同的初始条件下, 3种策略下滚转角均能稳定在0°附近逐渐收敛, 舵面偏转量如表1所示, 新型控制策略的舵偏需求较常规控制策略降低50%以上.

在姿态保持基础上, 成功实现了滚转机动控制, 常规控制策略整体跟踪效果良好, 新型控制策略存在超调/振荡, 但用舵量更小. 机动控制模式试验的舵面偏转量如表2所示, 在滚转角跟踪激励下, 新型控制策略的舵偏需求较常规控制策略降低45%以上.

表1 姿态保持模式各策略舵面偏转量对比Table 1 Comparison of deflection angles between different control strategies under attitude hold mode

表2 机动控制模式各策略舵面偏转量对比Table 2 Comparison of deflection angles between different control strategies under maneuver control mode

4 结论

围绕新型航天飞行器横航向耦合问题, 针对耦合失稳模式和新型控制策略, 开展了综合验证技术研究.

结合仿真分析和地面试验的特点, 制定了以动力学仿真为主、 CFD-RBD仿真和风洞虚拟飞行试验为辅的综合验证方案, 并重点给出了CFD-RBD仿真验证和高速风洞虚拟飞行试验验证结果.

采用CFD-RBD方法得到的飞行器运动特性与耦合失稳判据、 动力学线性仿真结果一致, 验证了荷兰滚失稳、 副翼操纵耦合失稳两种典型失稳模式及判据的正确性.

针对新型控制策略验证需求, 发展了高速风洞虚拟飞行试验技术, 成功开展了横航向姿态保持试验和横航向机动控制试验, 试验结果表明, 新型控制策略的舵偏需求较常规控制策略的舵偏需求降低45%以上.