潮汐调和分析方法的回顾与展望
2021-12-09吕咸青潘海东王雨哲
吕咸青, 潘海东, 王雨哲
潮汐调和分析方法的回顾与展望
吕咸青1, 2, 潘海东1, 2, 王雨哲1, 2
(1. 中国海洋大学物理海洋实验室, 山东 青岛 266100; 2. 青岛海洋科学与技术试点国家实验室, 山东 青岛 266237)
潮汐作为海洋中最普遍的运动过程, 与国民经济建设密切相关。潮汐调和分析作为使用最广泛的潮汐数据分析方法, 从1921年至今, 已历经100年的发展历程。本文对潮汐调和分析方法100年来的研究与发展进行总结与回顾, 并对其未来进行了展望, 致敬在潮汐调和分析方法发展及应用历程中有所建树的先贤和前辈。
潮汐; 调和分析; 振幅; 非平稳潮
海洋占据了地球表面71%, 与我们人类的生存发展密切相关。潮汐作为海洋中最普遍的运动过程之一, 是海水在天体引潮力作用下形成的某些特定频率上的周期性波动现象, 在垂直方向上表现为潮位的周期性升降, 而在水平方向上则表现为潮流的周期性运动[1]。潮汐的主要成因是地球表面上各点离月球和太阳的相对位置不同, 各点所受到的引潮力有所差异, 从而导致地球上的海水的相对运动[2]。潮汐的原动力——引潮力, 可分解为一系列频率(周期)的分力, 而每一个频率对应一个简谐振动, 称之为分潮[3]。对实际观测的水位资料进行经典潮汐调和分析可以求出各个主要分潮的振幅和迟角(称之为调和常数), 结合天文参数(交点因子和交点订正角)可以推算未来时刻的潮汐, 进行潮汐预报。潮汐与国民经济建设密切相关, 潮汐、潮流的准确预报在国防建设、航运交通、水产养殖、海洋资源开发、能源利用、环境保护、近海和远海工程建设以及海岸防护等各方面起着至关重要的作用[1]。
潮汐可以直接影响海洋内波、海洋环流、风暴潮、海气相互作用、海洋生态系统等。潮致混合可以将次表层冷水带到海洋表面, 进而使海表面温度降低[4]。一般认为潮致混合的强度与潮流流速的平方成正比[5-6], 而潮流流速存在周期约半月的大小潮循环和18.61 a循环, 这导致潮汐混合强度也存在半月和18.61 a循环, 最终海表面温度也存在相应的周期[7-11]。海面温度直接影响海表大气温度以及海洋生态系统[6, 9, 12]。Royer[13]指出在美国阿拉斯加锡特卡气温的30%的低频变化与18.61 a循环有关。Souza等[14]指出南加利福利亚海域海表面温度和硅藻丰度变化的半月周期与潮致混合有关。Tanaka等[15]发现在海气耦合模式里考虑潮汐混合的18.61 a循环可以提高年代际气候预报的准确性。
在层结的海洋中, 当正压潮流流经陆架、陆坡、海山、海洋中脊、岛弧等变化的海底地形时会产生与天文潮频率一致的海洋内波, 称为内潮[16-18]。地形变化越剧烈的海域, 往往会产生越显著的海洋内潮。海洋内潮可以引起海洋内部等密度面上百米的起伏[19-21], 在水平方向上可以传播1 000 km以上[22-24], 同时也会在深海产生强烈的剪切与混合[19, 21, 25-26]。海洋内潮作为从天文潮到混合过程的一个重要中间环节[19], 是连接不同尺度海洋动力过程的重要桥梁[27]。海洋内潮也是全球深海混合过程的主要能量来源。根据Munk等[28]的估算, 维持全球海洋的层结需要约2.1 TW的能量, 而其中约一半的能量来自深海潮汐。海洋内潮及其引起的海水混合会影响局地环流流场, 进而影响海域内的物质输运和生态系统[27, 29-30]。同时海洋内潮也是海洋内孤立波产生的一个重要因素[31], 而且内潮还能与其他频率的海洋波动(比如近惯性内波)和中尺度涡等发生相互作用[27, 32-36]。另外, 深海潮汐也是海洋物质输运的动力源泉, 特别是潮汐在海洋近底层可产生较强的剪切应力, 导致海底沉积物再悬浮和物质输运[37-41]。总之, 潮汐学的研究不仅具有重要的实际应用价值, 还具有重要的学术价值[1, 42-44]。
1 潮汐数据分析方法
经典潮汐调和分析是使用最广泛的潮汐数据分析方法。在经典潮汐调和分析方法中, 各个分潮的振幅和迟角都是常数, 这种假设对于平稳潮是合理的。但是对于河流潮汐、内潮等非平稳潮, 这种假设是不合理的。河流潮汐是天文潮与地形、底摩擦和河流径流非线性相互作用的结果。潮波在沿河传播的过程中会逐渐被扭曲和衰减[45-51]。对于这些高度非平稳潮汐时间序列, 经典潮汐调和分析方法只能得到各主要分潮的振幅和迟角的时间平均值。为了能够更好地理解潮与非潮过程的相互作用, 国内外学者开展了大量的相关研究。Jay等[52]首次将小波分析引入河流潮汐水位资料的分析, 小波分析相对于傅里叶分析和经典调和分析的优势在于它能得到某些频率振幅的时间变化, 因此被广泛用于包括河流潮汐在内的非平稳潮的分析[52-57]。然而, 小波分析虽然能反映信号时域和频域振幅的变化, 但是却丢失了潮频段分潮的分辨能力[58]。
Pan等[59]首次将经验模态分解(empirical mode decomposition, 简称EMD)引入河流潮汐的分析。经验模态分解[60]是依据数据自身的时间尺度特征来进行信号分解, 无须预先设定基函数。这一点与建立在先验性的谐波基函数(小波基函数)上的傅里叶分析(小波分析)方法具有实质性的差别。正是由于这样的特点, EMD方法在理论上可以应用于任何类型的信号的分解, 因而在处理非平稳及非线性数据上, 具有很高的信噪比, 有明显的优势。因此EMD方法一经提出就在不同的工程领域得到了广泛的应用, 例如在海洋、大气、天体观测资料与地震记录分析、机械故障诊断、密频动力系统的阻尼识别以及大型土木工程结构的模态参数识别方面[59, 61-65]。EMD方法能使复杂信号分解为有限个本征模函数(intrinsic mode function, 简称IMF), 所分解出来的各IMF分量包含了原信号的不同时间尺度的局部特征信号。Flandrin等[66]研究表明EMD是一个二分滤波器(每个EMD模态的周期都近似是前面的2倍)。对于河流潮汐数据进行EMD分解得到的第一模态代表半日潮, 第二模态代表全日潮, 剩余模态的叠加是平均海平面(mean water level, MWL)。EMD成功捕捉到了全日分潮, 半日分潮以及平均海平面的由径流引起的非平稳变化特征。和小波分析一样, EMD同样丢失了潮频段分潮的分辨能力[58-59]。张亮等[67]使用了改进的集合经验模态分解(MEEMD)对海洋潮汐进行分析, 该方法解决了EMD的模态混淆问题, 但是仍然不具备潮频段分潮的分辨能力。
Matte等[58]首次尝试改进经典潮汐调和分析模型,使之能应用于河流潮汐。Matte等[58]基于Kukulka等[68-69]的潮汐-径流相互作用的理论框架, 将非平稳的外力强迫直接引入到调和分析基础函数中, 开发了专门用于河流潮汐分析的工具包NS_TIDE。Matte等[58]将NS_TIDE用于分析美国哥伦比亚河的Vancouver验潮站的水位数据, Gan等[70]和Yu等[71]将NS_TIDE应用于中国长江口水位数据分析, 他们的结果均表明NS_TIDE在河流潮汐数据分析中的表现远远优于经典调和分析工具包T_TIDE[72]。
Jin等[73]提出了非平稳潮汐调和分析方法(enhanced harmonic analysis, EHA), 并首次应用于内潮流速资料的分析, 理念上将经典调和分析理论中的振幅和迟角由常数改进为随时间变化的函数, 将独立点方案[44, 74-76]和三次样条插值方法引入调和分析方法中, 利用最小二乘方法对随时间变化的振幅和迟角进行求解。Pan等[77]基于广泛使用的T_TIDE工具包为EHA开发了S_TIDE工具包, 并首次使用S_TIDE研究了美国哥伦比亚河口的潮汐-径流相互作用。相比NS_TIDE只能应用于河流潮汐, S_TIDE理论上可以应用于所有类型的潮汐。
NS_TIDE和S_TIDE作为潮汐调和分析模型的最新进展, 引起了大家的兴趣和关注。本文首先回顾经典潮汐调和分析模型的原理, 然后重点介绍NS_ TIDE和S_TIDE模型的原理, 指出它们的优缺点, 并探讨未来潮汐调和分析模型的发展方向。
2 经典潮汐调和分析模型
在经典潮汐调和分析模型中[如式(1)所示], 水位被认为是一系列三角函数线性叠加的结果[78-81], 每一个三角函数都代表了一个分潮:
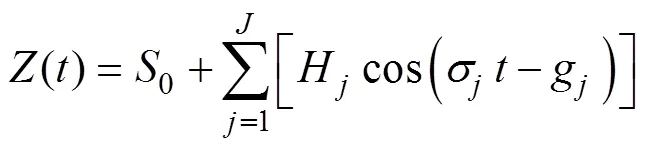
()是时刻观测到的水位,σ、H以及g是第个分潮对应的角速度、振幅和迟角。是分辨的分潮的个数。0是平均海平面。式(1)可以使用变量a和b线性化表达并改写为式(2):
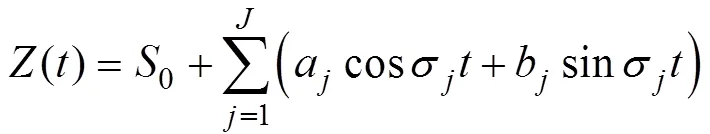
式(1)中
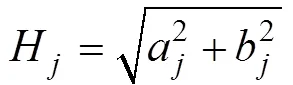
在做线性回归时, 根据式(2)用矩阵的形式表示, 即式(4):
=, (4)
其中,是观测水位矩阵,是已知的系数矩阵,是待求解的未知参数矩阵, 具体表达如式(5)和(6)所示:

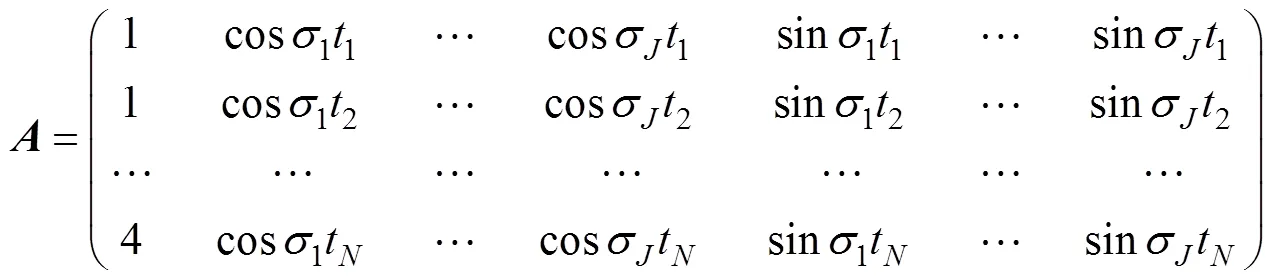
根据最小二乘法,的解为:
s=(T)–1T. (7)
为了减小潮汐调和分析所求得的分潮振幅和迟角的置信区间, Godin[82]提出了瑞利准则来限制调和分析里使用的分潮的个数[式(8)]:
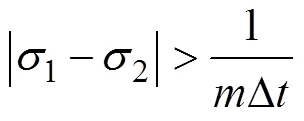
对美国哥伦比亚河5个验潮站观测的水位数据应用经典潮汐调和分析(借助于T_TIDE工具包), 结果如表1所示。Astoria是离海洋最近的站点, 河流径流影响较小, 经典潮汐调和分析回报水位解释了原信号96.7%的变化, 均方根误差0.15 m, 最大绝对误差1.18 m。潮波在沿河道向内陆传播的过程中, 受河流径流的影响越来越大, 而经典潮汐调和分析并没有考虑潮汐-径流的非线性相互作用, 导致离海洋越远的站点, T_TIDE的表现就越差(表1)。Vancouver是离海洋最远的站, 也是T_TIDE表现最差的, 其回报的水位只能解释原信号的52.4%, 均方根误差是1.60 m, 最大绝对误差是4.16 m。
3 非平稳潮汐调和分析模型NS_TIDE
3.1 NS_TIDE模型介绍
经典潮汐调和分析模型认为每一个分潮都是完美的三角函数, 即分潮的振幅和迟角都是不随时间变化的常数。在感潮河段, 由于潮汐-径流非线性相互作用, 导致主要分潮的振幅和迟角不再是常数, 而是河流径流的非线性函数。由于不合理的平稳性假设, 经典潮汐调和分析方法在河口地区表现不尽人意。基于Kukulka 等[68-69]的潮汐-径流相互作用的理论模型, Matte等[58, 83]在T_TIDE的基础上开发了专门用于河流潮汐数据分析的工具包NS_TIDE。NS_TIDE认为分潮的振幅和迟角都是随时间变化的[式(9)], 并将非平稳的外力强迫(河流径流和外海潮汐)直接引入到调和分析基础函数中[式(10)]。
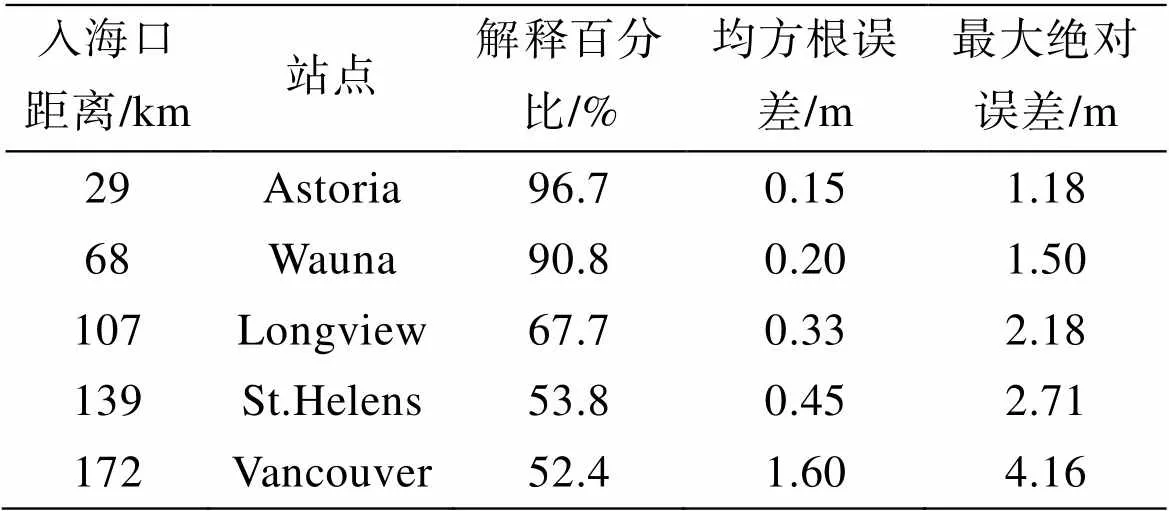
表1 T_TIDE在哥伦比亚河下游站点的表现

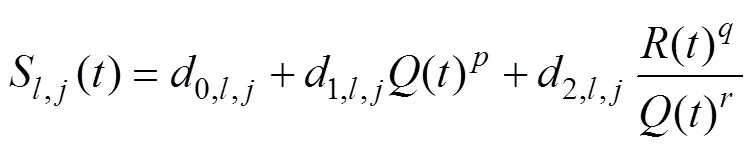
其中,代表河流径流,代表外海参考站的全日潮差。代表分析的分潮总个数。是模型系数(=0代表亚潮模型系数,=1, 2代表潮汐-径流模型系数)。、以及是待定的常数, 其理论值由Kukulka 等[68-69]给出。如果知道、、, 通过最小二乘的方法就能求出未知的模型系数, 进而量化非平稳外力对于潮汐振幅和迟角的影响。在NS_TIDE中, 为了减少离群值对于调和分析结果的影响, NS_TIDE 使用了迭代权重最小二乘法(the iteratively reweighted least squares, IRLS)[84-85]。
对于河口潮等非平稳潮, 瑞利准则[式(8)]是不适用的。Munk等[86]指出潮汐谱线周围形成的尖点宽度与非线性强迫的低频谱有关。从这一事实出发, NS_TIDE定义了适用于非平稳潮的瑞利准则, 它主要考虑到主要分潮附近的小分潮对于主要分潮能谱的扭曲:
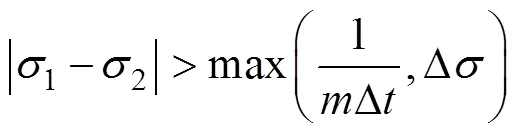
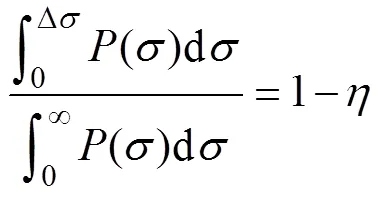
3.2 NS_TIDE模型优缺点
NS_TIDE不仅保持了潮频段分潮的分辨能力, 而且还可以量化非平稳外力(河流径流)对于潮汐非平稳变化的贡献。因此, NS_TID在美国哥伦比亚河[58-59, 77]、加拿大圣劳仑斯河[58, 87-88]、中国长江[70-71, 89]和珠江[90]等全球各大河口都得到了广泛应用。但是NS_TIDE也存在一些不足[59, 77]。第一, 河流高频径流数据的缺乏会限制NS_TIDE的使用。第二, NS_TIDE基于潮汐-径流相互作用模型, 这也就导致了NS_TIDE不能用于其他的非平稳潮(比如内潮)。第三, NS_TIDE需要河流参考站的逐时水位数据。而且, NS_TIDE只考虑了潮汐-径流的相互作用, 忽略了其他的重要物理过程比如沿岸上升流[91]对于水位变化的影响。第四, NS_TIDE的待定指数需要进行迭代计算和优化, 导致计算效率降低。
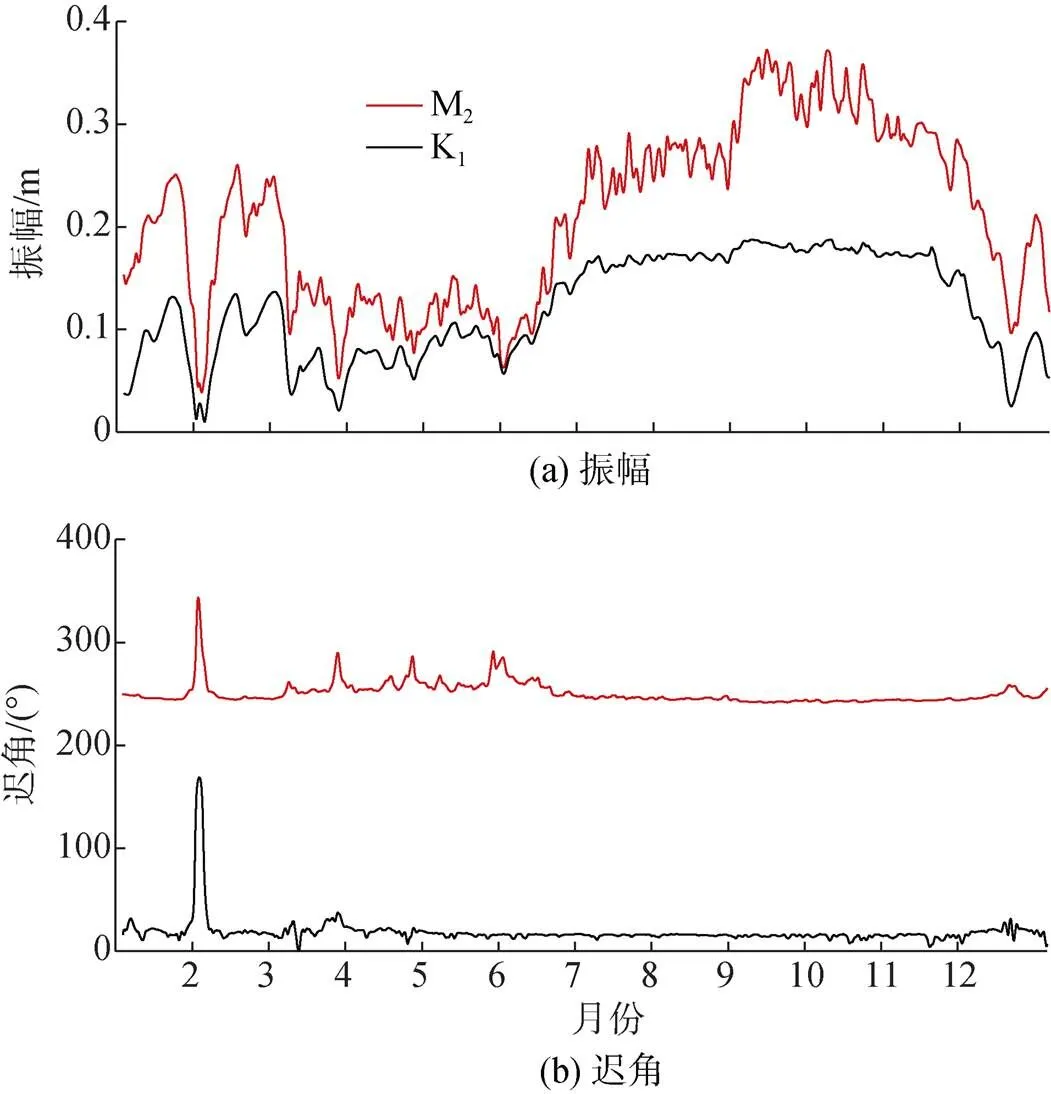
图1 NS_TIDE得到的2003年Vancouver处的M2和K1的振幅(a)和迟角(b)
4 非平稳潮汐调和分析模型S_TIDE
4.1 S_TIDE模型介绍
与NS_TIDE类似, 如式(13)所示, S_TIDE同样认为分潮的振幅和迟角是随时间变化的:
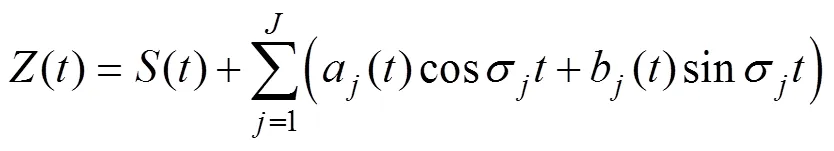
但是不同于NS_TIDE, 在S_TIDE中, 式(13)的求解使用了独立点方案[44, 73, 92-95]。独立点方案的基本思想是基于样条函数方法。如图2所示, 假定调和变量(比如振幅)是随时间变化的(图2中黑色实线), X={x1, x2, x3,…, x9} 是不同的时刻。首先, 选择= {x1, x3, x5, x7, x9}作为独立点(independent points, IPs)代表整个变量空间。然后, 独立点处的调和变量的值(图2中的红色圆圈)通过特定的算法可以求解(细节稍后给出)。最后, 调和变量在非独立点处(x2, x4, x6, x8)的值可以通过独立点处的插值得到。
注: 红色的点为独立点, 黑色的点为非独立点
S_TIDE的求解过程可以表示为如下步骤。对于平均海平面和第个分潮潮汐调和变量(a和b), 在时间域上均匀选取一系列点作为独立点(标记为S,a和b), 而非独立点处的值可以通过独立点处的插值得到。因此, 随时间变化的MWL和调和变量可以用独立点来表达S、a和b:
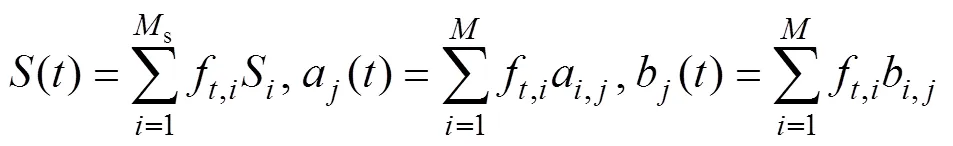
其中,f是第个独立点在时刻的插值权重, 只与选用的插值方法有关。s和分别是MWL和分潮使用的独立点个数。要注意的是, 目前S、a和b还是待定的, 但是基于独立点方案, 随时间变化的()a()和b()被表达成了独立点(S,a,b)处值的线性叠加[式(14)]。将式(13)和(14)组合得到式(15):
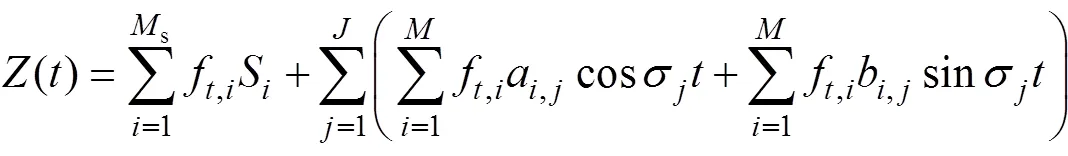
三次样条插值由于其稳定、收敛和光滑的性质在数据处理中得到了广泛使用[44, 60, 96-97]。因此, S_TIDE选择了三次样条插值连接独立点和非独立点。关于三次样条插值权重的具体计算公式可以参考Pan等[77], 这里不再赘述。
党的十九大提出乡村振兴战略并写入党章,把“三农”工作的重要性提升到前所未有的高度。作为当前农村工作的重中之中,精准扶贫对乡村发展具有重大意义,同时与乡村振兴具有内在统一性和显在的自洽性。探讨二者深层的逻辑关系和内在机理,思考以精准扶贫推进乡村振兴的现实路径,有助于进一步理解和领悟习近平关于“三农”工作的重要论述和更好地推进乡村振兴的伟大事业,因而具有深刻的理论意义和重要的现实意义。
如果有个时刻的水位观测值, 即=1,2,…,Z, 在=1,2,…,t,时刻, 可以得到下面的方程组:
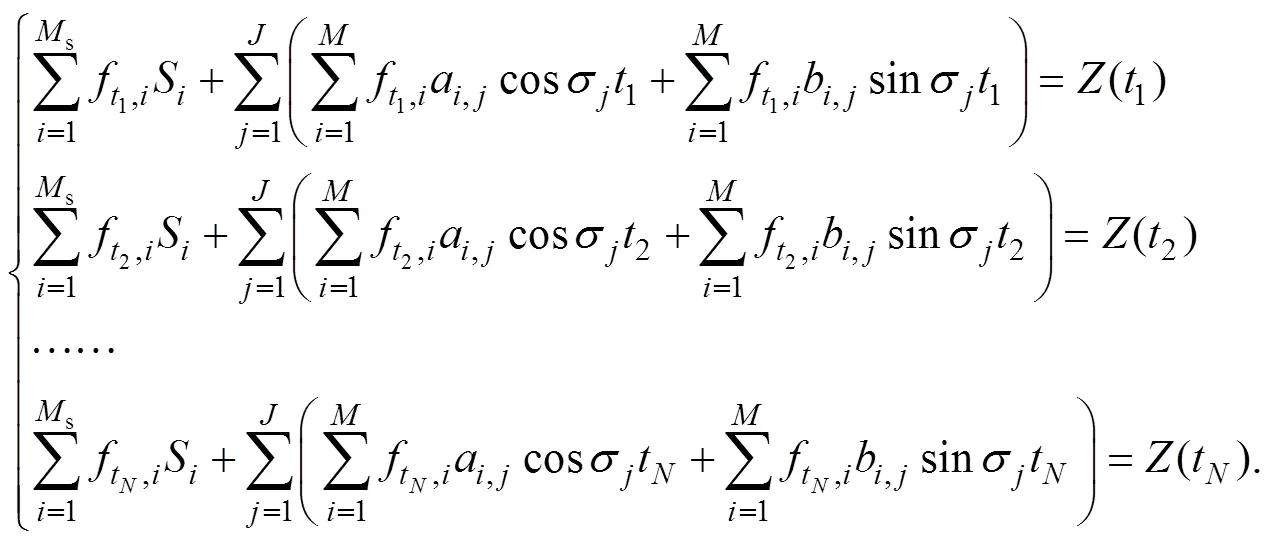
方程组(16)里有(2∙s)个未知参数, 当观测数远远大于(2∙s)时可以通过最小二乘法来求解这些未知参数(S,a和b)。一旦独立点处的值确定, 就可以三次样条插值得到时间变化的MWL、分潮振幅和迟角。
在做线性回归时, 与经典潮汐调和分析类似, 式(16)也可以写成矩阵的形式, 即式(17):
=, (17)
其中是观测水位矩阵,是已知的系数矩阵,是待求解的未知参数矩阵, 具体表达如式(18)、(19)和(20)所示:
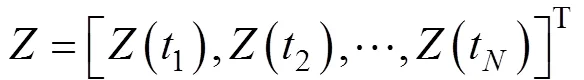
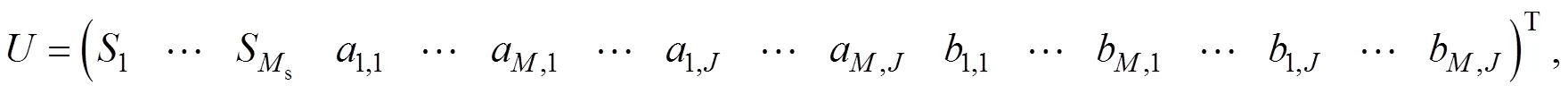
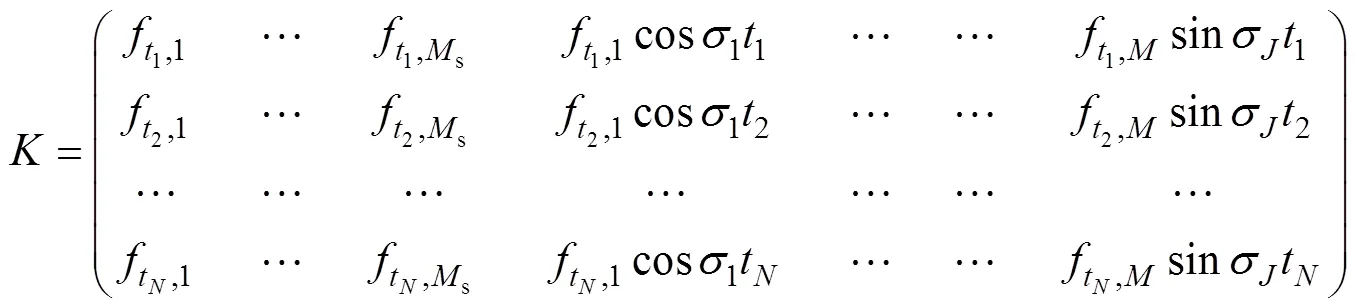
根据最小二乘法,的最优解为:
s=(T)–1T. (21)
独立点个数和使用的分潮是S_TIDE最核心的两个输入参数, 如果这两个参数取值不合适, S_TIDE输出结果可能是没有物理意义的。根据目前的研究[77, 98], 独立点个数越多, S_TIDE得到的分潮振幅和迟角的变化就越复杂; 独立点越少, 得到的振幅和迟角的变化就越简单。当独立点个数为2时, S_TIDE得到的分潮振幅和迟角的变化是线性的; 当独立点个数为1时, S_TIDE得到的分潮振幅和迟角都是不随时间变化的, 与经典调和分析结果是完全一致的。从某种意义上来说, 经典潮汐调和分析模型可以看成是S_TIDE在独立点为1时的一个特例。独立点个数和分潮的个数是相互制约的。使用的独立点越多, S_TIDE得到的分潮振幅和迟角的变化就越复杂, 能分辨的分潮就越少, 计算得到的分潮振幅里来自邻近的未分辨的分潮的贡献就越大, 反之亦然。
以下以M2分潮振幅的年循环为例, 介绍为什么在S_TIDE模型里独立点个数和分潮的个数是相互制约的。如式(22)所示,σ、h以及g是M2分潮振幅年循环的频率、振幅和迟角,M2、M2以及M2是M2分潮振幅的频率、振幅和迟角,是时间。对式(22)做积化和差展开, 得到式(23)。虽然式(22)与(23)在数学上是完全等价的, 但是它们却代表了对同一信号的两种完全不同的解读方式。式(22)认为信号里只存在一个频率, 那就是M2分潮的频率, 但是M2分潮振幅是存在年变化的。式(23)中出现3个分潮的频率, 分别是M2、H1和H2这3个分潮的频率, 而且这3个分潮振幅都是不随时间变化的常数。式(22)代表了S_TIDE理解信号的方式, 即分潮的振幅和迟角是时间变化的; 而式(3)—(10)则代表了T_TIDE理解信号的方式, 即分潮的振幅和迟角都是常数。如果要用S_TIDE提取M2分潮振幅的年变化, 那么在S_TIDE模型里, H1和H2分潮不能区分, 因为H1和H2分潮是由于M2分潮的年循环产生的。
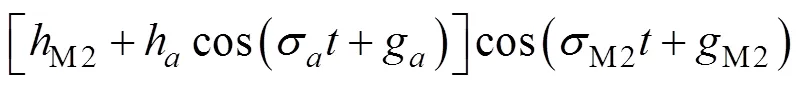
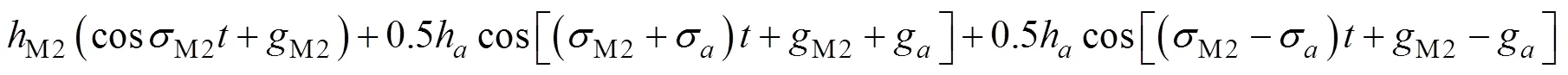
S_TIDE在哥伦比亚河的表现要略优于NS_ TIDE。以Vancouver验潮站为例: S_TIDE回报的水位解释了原始观测99.1%的方差变化, 均方根误差为0.075 m, 最大绝对误差为0.48 m。图3展示了S_TIDE回报水位, 几乎与观测水位一致, 回报的残差非常小。相比之下, T_TIDE的回报误差非常大。
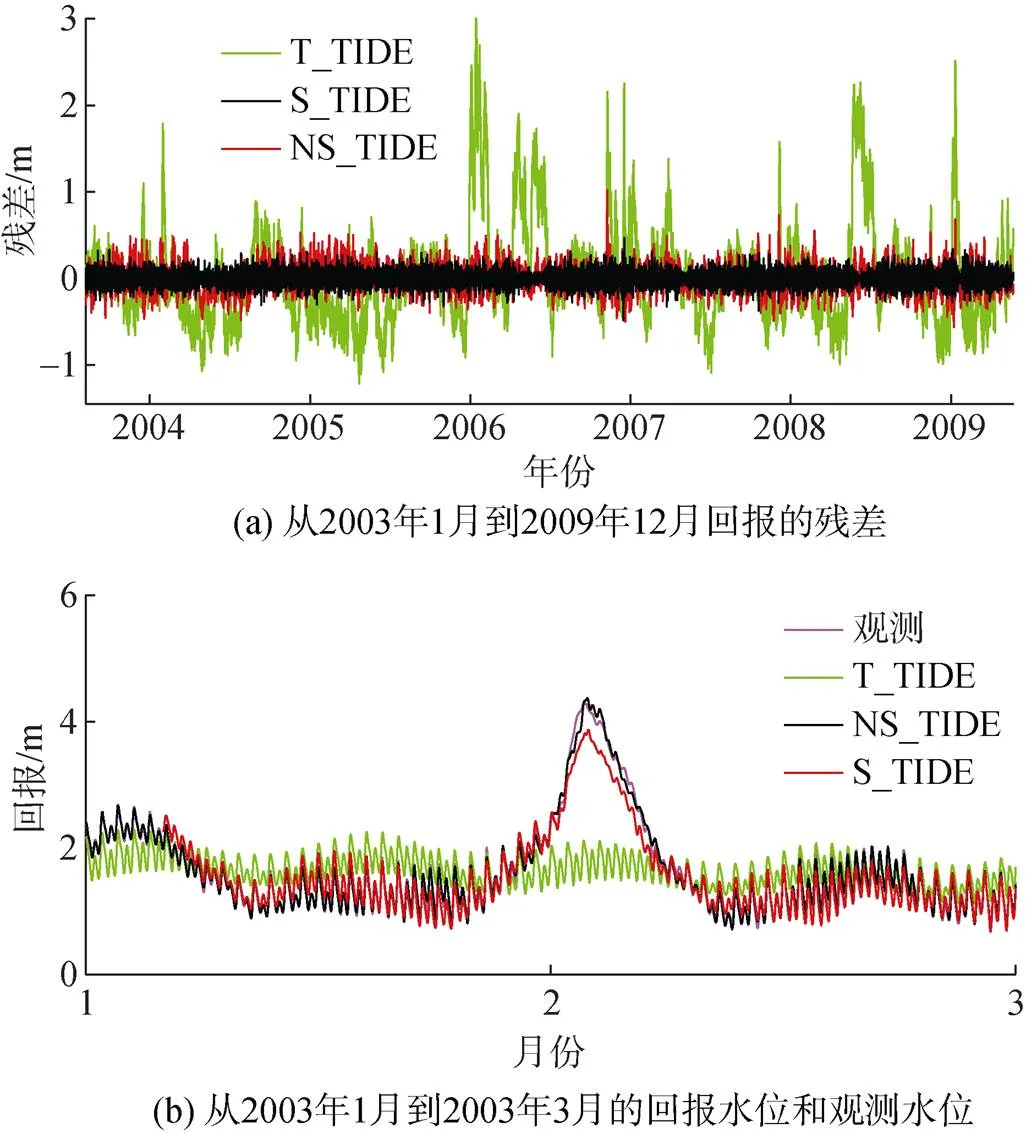
图3 (a)在Vanvouver, T_TIDE, NS_TIDE和S_TIDE结果比较
4.2 S_TIDE模型优点
1) 相比小波分析和NS_TIDE, S_TIDE更加简单易懂, 更容易实现。由S_TIDE得到的结果与经验模态分解, 小波分析还有NS_TIDE高度一致, 也符合河口潮解析理论。但是相比NS_TIDE, S_TIDE回报更加准确。
2) 与经典潮汐调和分析类似, S_TIDE只假定预先知道潮汐频率,无需知道其他的动力过程。也就是说S_TIDE不像NS_TIDE那样依赖于河流径流数据或者其他外界强迫数据, 这使得S_TIDE可以广泛应用于其他非平稳潮汐过程(比如内潮)。不仅如此, 尽管S_TIDE是为非平稳潮设计的, 但是其实它也可以用于平稳潮, 可以用来分析振幅和水位的长期变化和季节变化等。
3) 可以使用S_TIDE来准确分离水位里的潮汐和亚潮波动。也可以通过调整独立点的个数来提取MWL、分潮振幅和迟角在不同时间尺度上的波动。
4.3 S_TIDE模型的不足
1) S_TIDE是处理非平稳非线性数据的有力工具。NS_TIDE可以用于预报; 而S_TIDE目前还未实现, 尚需深化研究。
2) 当独立点个数较大时, 相比其他的方法, S_ TIDE需要更多的计算资源和时间。另外, 太多的独立点可能会导致计算机内存的溢出和不符合实际的结果。例如, 对于哥伦比亚河Vancouver验潮站7年的水位数据, 当分潮的独立点超过了500个时, 反演得到的振幅的大小潮变化由于过度拟合被明显夸大了。因此, 在使用S_TIDE时要非常谨慎选择独立点个数和使用的分潮。
5 结论
经典潮汐调和分析作为使用最广泛的潮汐数据分析方法, 从1921年至今, 已历经100年的发展历程。Doodson[78-80]发展并完善了经典的潮汐调和分析理论。方国洪于1960年发展了Doodson短期观测的分析方法, 对引潮势进行了准调和展开, 提出了潮汐分析和预报的准调和分析方法[99-101], 为我国的潮汐、潮流分析预报工作做出了重要贡献。当代我国的潮汐潮流研究, 陈宗镛[102]的《潮汐学》, 方国洪等[1]的《潮汐和潮流的分析和预报》, 黄祖珂等[103]的《潮汐原理与计算》等专著发挥了重要作用。
经典调和分析方法理论上没有考虑季节变化, 而主要分潮的季节变化是客观存在的, 亟待准确的刻画和提取。尽管在经典调和分析的框架下, 能够获取主要分潮的季节变化, 但在具体求解过程中必须假定某个时间段内各分潮的调和常数是不变的, 而这个时间段长度如何确定是个无法解决的问题: 这个时间段长度过短则无法准确分离不同分潮, 过长则无法准确提取出各个分潮随时间变化; 需要特别指出的是上述的求解过程不可避免地会弱化振幅(迟角)的变化幅度。根据调和分析理论和方法的发展趋势和现实需求, 潮汐调和分析模型研究未来可能的发展方向之一是改进经典的调和分析方法, 把经典调和分析方法中主要分潮的调和常数(振幅和迟角)推广位变化的振幅(迟角), 开展变化振幅(迟角)获取的理论和方法研究。
致谢: 谨以此文致敬在潮汐调和分析模型发展及应用历程中有所建树的先贤和前辈们, 特别感谢引领我入门物理海洋学研究的授业恩师方国洪先生。本文使用的S_TIDE工具包可以从如下网址获取: https://www.researchgate.net/project/ A-non-stationary-tidal-analysis-toolbox-S-TIDE。
[1] 方国洪, 郑文振, 陈宗镛, 等. 潮汐和潮流的分析和预报[M]. 北京: 海洋出版社, 1986.
FANG Guohong, ZHENG Wenzhen, CHEN Zongyong, et al. Analysis and prediction of tides and tidal currents[M]. Beijing: Ocean Press, 1986.
[2] 叶安乐, 李凤岐. 物理海洋学[M]. 青岛: 青岛海洋大学出版社, 1992.
YE Anle, LI Fengqi. Physical oceanography[M]. Qingdao: Qingdao Ocean University Press, 1992.
[3] 冯士筰, 李凤岐, 李少菁. 海洋科学导论[M]. 北京: 高等教育出版社, 1999.
FENG Shizuo, LI Fengqi, LI Shaojing. Introduction to ocean science[M]. Beijing: Higher Education Press, 1999.
[4] SUSANTO R D, PAN J, DEVLIN A T. Tidal mixing signatures in the Hong Kong coastal waters from satellite-derived sea surface temperature[J]. Remote Sensing, 2019, 11(1): 5.
[5] FFIELD A, GORDON A L. Tidal mixing signatures in the Indonesian seas[J]. Journal of Physical Oceanography, 1996, 26(9): 1924-1937.
[6] RAY R D, SUSANTO R D. Tidal mixing signatures in the Indonesian seas from high-resolution sea surface temperature data[J]. Geophysical Research Letters, 2016, 43(15): 8115-8123.
[7] LODER J W, GARRETT C. The 18.6-year cycle of sea surface temperature in shallow seas due to variations in tidal mixing[J]. Journal of Geophysical Research: Oceans, 1978, 83(C4): 1967-1970.
[8] PINEDA J. An internal tidal bore regime at nearshore stations along western U.S.A.: Predictable upwelling within the lunar cycle[J]. Continental Shelf Research, 1995, 15(8): 1023-1041.
[9] OSAFUNE S, YASUDA I. Bidecadal variability in the intermediate waters of the northwestern subarctic Pacific and the Okhotsk Sea in relation to 18.6-year period nodal tidal cycle[J]. Journal of Geophysical Research: Oceans, 2006, 111(5): C05007
[10] YASUDA I, OSAFUNE S, TATEBE H. Possible explanation linking 18.6-year period nodal tidal cycle with bi-decadal variations of ocean and climate in the North Pacific[J]. Geophysical Research Letters, 2006, 33(8): 153-172.
[11] YNDESTAD H, TURRELL W R, OZHIGIN V. Lunar nodal tide effects on variability of sea level, temperature, and salinity in the Faroe-Shetland Channel and the Barents Sea[J]. Deep-Sea Research Part I: Oceanographic Research Papers, 2008, 55(10): 1201-1217.
[12] YNDESTAD H. The influence of the lunar nodal cycle on Arctic climate[J]. ICES Journal of Marine Science, 2006, 63(3): 401-420.
[13] ROYER T C. High-latitude oceanic variability associated with the 18.6-year nodal tide[J]. Journal of Geophysical Research: Oceans, 1993, 98(C3): 4639-4644.
[14] SOUZA A J, PINEDA J. Tidal mixing modulation of sea-surface temperature and diatom abundance in Southern California[J]. Continental Shelf Research, 2001, 21(6/7): 651-666.
[15] TANAKA Y, YASUDA I, HASUMI H, et al. Effects of the 18.6-yr modulation of tidal mixing on the north pacific bidecadal climate variability in a coupled climate model[J]. Journal of Climate, 2012, 25(21): 7625-7642.
[16] 戴德君. 若干地形下内波传播及内潮生成问题的理论解[D]. 青岛: 中国海洋大学, 2003.
DAI Dejun. Theoretical solutions of propagation of internal waves and generation of internal tides over some kinds of topographies[D]. Qingdao: Ocean University of China, 2003.
[17] 邬丽丹. 内潮生成机制以及吕宋海峡周边海域内潮的季节变化研究[D]. 青岛: 中国海洋大学, 2013.
WU Lidan. Mechanism of internal tide generation and seasonal variation of internal tides around the Luzon Strait[D]. Qingdao: Ocean University of China, 2013.
[18] CAO A, GUO Z, LV X, et al. Coherent and incoherent features, seasonal behaviors and spatial variations of internal tides in the northern South China Sea[J]. Journal of Marine Systems, 2017, 172: 75-83.
[19] RUDNICK D L, BOYD T J, BRAINARD R E, et al. From tides to mixing along the Hawaiian Ridge[J]. Science, 2003, 301(5631): 355-357.
[20] ALFORD M H, MACKINNON J A, NASH J D, et al. Energy flux and dissipation in luzon strait: Two tales of two ridges[J]. Journal of Physical Oceanography, 2011, 41(11): 2211-2222.
[21] ALFORD M H, PEACOCK T, MACKINNON J A, et al. The formation and fate of internal waves in the South China Sea[J]. Nature, 2015, 521(7550): 65-69.
[22] RAY R D, MITCHUM G T. Surface manifestation of internal tides generated near Hawaii[J]. Geophysical Research Letters, 1996, 23(16): 2101-2104.
[23] ZHAO Z, ALFORD M H, MACKINNON J A, et al. Long-range propagation of the semidiurnal internal tide from the Hawaiian Ridge[J]. Journal of Physical Oceanography, 2010, 40(4): 713-736.
[24] ZHAO Z. Internal tide radiation from the Luzon Strait[J]. Journal of Geophysical Research: Oceans, 2014, 119(8): 5434-5448.
[25] TIAN J, YANG Q, ZHAO W. Enhanced diapycnal mixing in the South China Sea[J]. Journal of Physical Oceanography, 2009, 39(12): 3191-3203.
[26] TIAN J, ZHOU L, ZHANG X. Latitudinal distribution of mixing rate caused by the M2 internal tide[J]. Journal of Physical Oceanography, 2006, 36(1): 35-42.
[27] 曹安州. 南海北部内潮生成机制和传播特征研究[D]. 青岛: 中国海洋大学, 2016.
CAO Anzhou. On the generation and propagation of internal tides in the northern South China Sea[D]. Qingdao: Ocean University of China, 2016.
[28] MUNK W, WUNSCH C. Abyssal recipes II: Energetics of tidal and wind mixing[J]. Deep-Sea Research Part I: Oceanographic Research Papers, 1998, 45(12): 1977- 2010.
[29] 陈海波. 一个等密度坐标内潮伴随同化模型的数值建模及其应用研究[D]. 青岛: 中国海洋大学, 2012.
CHEN Haibo. Development and application of an isopycnic-coordinate numerical model for simulation of internal tides with adjoint assimilation method[D]. Qingdao: Ocean University of China, 2012.
[30] 苗春葆. 三维等密度坐标数值模型的建立以及南海内潮的数值模拟. 青岛: 中国海洋大学, 2012.
MIAO Chunbao. Development of an isopycnic-coordinate numerical model and the simulation of internal tides in the South China Sea[D]. Qingdao: Ocean University of China, 2012.
[31] CHAO S Y, KO D S, LIEN R C, et al. Assessing the west ridge of Luzon Strait as an internal wave mediator[J]. Journal of Oceanography, 2007, 63(6): 897-911.
[32] XIE X H, CHEN G Y, SHANG X , et al. Evolution of the semidiurnal (M2) internal tide on the continental slope of the northern South China Sea[J]. Geophysical Research Letters, 2008, 35(13): L13604.
[33] XIE X H, SHANG X D, CHEN G Y, et al. Variations of diurnal and inertial spectral peaks near the bi-diurnal critical latitude[J]. Geophysical Research Letters, 2009, 36(2): 349-363.
[34] XIE X H, SHANG X D, VAN HAREN H, et al. Observations of parametric subharmonic instability-induced near-inertial waves equatorward of the critical diurnal latitude[J]. Geophysical Research Letters, 2011, 38(5): L05603
[35] GUAN S, ZHAO W, HUTHNANCE J, et al. Observed upper ocean response to typhoon Megi (2010) in the Northern South China Sea[J]. Journal of Geophysical Research: Oceans, 2014, 119(5): 3134-3157.
[36] DUNPHY M, LAMB K G. Focusing and vertical mode scattering of the first mode internal tide by mesoscale eddy interaction[J]. Journal of Geophysical Research: Oceans, 2014, 119(1): 523-536.
[37] FRIEDRICHS C T, WRIGHT L D. Resonant internal waves and their role in transport and accumulation of fine sediment in Eckernförde Bay, Baltic Sea[J]. Continental Shelf Research, 1995, 15(13): 1697-1721.
[38] RIBBE J, HOLLOWAY P E. A model of suspended sediment transport by internal tides[J]. Continental Shelf Research, 2001, 21(4): 395-422.
[39] TURNEWITSCH R, REYSS J L, NYCANDER J, et al. Internal tides and sediment dynamics in the deep sea-Evidence from radioactive 234Th/238U disequilibria[J]. Deep-Sea Research Part I: Oceanographic Research Papers, 2008, 55(12): 1727-1747.
[40] PEINE F, TURNEWITSCH R, MOHN C, et al. The importance of tides for sediment dynamics in the deep sea-Evidence from the particulate-matter tracer 234Th in deep-sea environments with different tidal forcing[J]. Deep-Sea Research Part I: Oceanographic Research Papers, 2009, 56(7): 1182-1202.
[41] 赵玖强, 张艳伟, 刘志飞, 等. 南海北部深海潮汐的季节性变化特征[J]. 中国科学: 地球科学, 2019, 49: 717-730.
ZHAO Jiuqiang, ZHANG Yanwei, LIU Zhifei, et al. Seasonal variation characteristics of deep-sea tides in the northern South China Sea[J]. Scientia Sinica (Terrae), 2019, 49: 717-730.
[42] LU X, ZHANG J. Numerical study on spatially varying bottom friction coefficient of a 2D tidal model with adjoint method[J]. Continental Shelf Research, 2006, 26(16): 1905-1923.
[43] 张继才. 三维正压潮汐潮流伴随同化模型数值建模及应用研究[D]. 青岛: 中国海洋大学, 2008.
ZHANG Jicai. Development and application of a three- dimensional numerical barotropic adjoint assimilation tidal model[D]. Qingdao: Ocean University of China, 2008.
[44] PAN H, GUO Z, LV X. Inversion of tidal open boundary conditions of the M2 constituent in the bohai and yellow seas[J]. Journal of Atmospheric and Oceanic Technology, 2017, 34(8): 1661-1672.
[45] JAY D A. Green’s law revisited: Tidal long-wave propagation in channels with strong topography[J]. Journal of Geophysical Research, 1991, 96(C11): 20585.
[46] GODIN G. Modification of river tides by the discharge[J]. Journal of Waterway, Port, Coastal and Ocean Engineering, 1985, 111(2): 257-274.
[47] GODIN G. The propagation of tides up rivers with special considerations on the upper Saint Lawrence river[J]. Estuarine, Coastal and Shelf Science, 1999, 48(3): 307- 324.
[48] CAI H, SAVENIJE H H G, JIANG C. Analytical approach for predicting fresh water discharge in an estuary based on tidal water level observations[J]. Hydrology and Earth System Sciences, 2014, 18(10): 4153- 4168.
[49] GUO L, VAN DER WEGEN M, ROELVIN J A, et al. The role of river flow and tidal asymmetry on 1-D estuarine morphodynamics[J]. Journal of Geophysical Research F: Earth Surface, 2014, 119(11): 2315-2334.
[50] GUO L, VAN DER WEGEN M, WANG Z B, et al. Exploring the impacts of multiple tidal constituents and varying river flow on long-term, large-scale estuarine morphodynamics by means of a 1-D model[J]. Journal of Geophysical Research F: Earth Surface, 2016, 121(5): 1000-1022.
[51] LU SHENG, CHAOFENG T, LEE DONG YOUNG, et al. Propagation of tidal waves up in Yangtze Estuary during the dry season[J]. Journal of Geophysical Research: Oceans, 2015, 120(9): 6445-6473.
[52] JAY D A, FLINCHEM E P. A comparison of methods for analysis of tidal records containing multi-scale non-tidal background energy[J]. Continental Shelf Research, 1999, 19(13): 1695-1732.
[53] JAY D A, KUKULKA T. Revising the paradigm of tidal analysis - The uses of non-stationary data[J]. Ocean Dynamics, 2003, 53(3): 110-125.
[54] SASSI M G, HOITINK A J F. River flow controls on tides and tide-mean water level profiles in a tidal freshwater river[J]. Journal of Geophysical Research: Oceans, 2013, 118(9): 4139-4151.
[55] GUO L, VAN DER WEGEN M, JAY D A, et al. River- tide dynamics: Exploration of nonstationary and nonlinear tidal behavior in the Yangtze River estuary[J]. Journal of Geophysical Research: Oceans, 2015, 120(5): 3499- 3521.
[56] HOITINK A J F, JAY D A. Tidal river dynamics: Implications for deltas[J]. Reviews of Geophysics, 2016, 54(1): 240-272.
[57] LOSADA M A, DÍEZ-MINGUITO M, REYES-MERLO M. Tidal-fluvial interaction in the Guadalquivir River Estuary: Spatial and frequency-dependent response of currents and water levels[J]. Journal of Geophysical Research: Oceans, 2017, 122(2): 847-865.
[58] MATTE P, JAY D A, ZARON E D. Adaptation of classical tidal harmonic analysis to nonstationary tides, with application to river tides[J]. Journal of Atmospheric and Oceanic Technology, 2013, 30(3): 569-589.
[59] PAN H, GUO Z, WANG Y, et al. Application of the EMD method to river tides[J]. Journal of Atmospheric and Oceanic Technology, 2018, 35(4): 809-819.
[60] HUANG N E, SHEN Z, LONG S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the Royal Society A, 1996, 454(1971): 903-995.
[61] EZER T. Sea level rise, spatially uneven and temporally unsteady: Why the U.S. East Coast, the global tide gauge record, and the global altimeter data show different trends[J]. Geophysical Research Letters, 2013, 40(20): 5439-5444.
[62] EZER T, CORLETT W B. Is sea level rise accelerating in the Chesapeake Bay? A demonstration of a novel new approach for analyzing sea level data[J]. Geophysical Research Letters, 2012, 39(19): L19605.
[63] EZER T, HAIGH I D, WOODWORTH P L. Nonlinear Sea-Level Trends and Long-Term Variability on Western European Coasts[J]. Journal of Coastal Research, 2016, 32(4): 744-755.
[64] CHENG Y, EZER T, ATKINSON L P, et al. Analysis of tidal amplitude changes using the EMD method[J]. Continental Shelf Research, 2017, 148: 44-52.
[65] CHENG Y, EZER T, HAMLINGTON B D. Sea level acceleration in the china seas[J]. Water (Switzerland), 2016, 8(7): 293.
[66] FLANDRIN P, RILLING G, GONÇALVÉS P. Empirical mode decomposition as a filter bank[J]. IEEE Signal Processing Letters, 2004, 11(2 PART I): 112- 114.
[67] 张亮, 张佳丽, 张学峰, 等. 基于希尔伯特-黄变换的潮汐分析方法研究[J]. 天津大学学报: 自然科学与工程技术版, 2020(7): 725-735.
ZHANG Liang, ZHANG Jiali, ZHANG Xuefeng, et al. Study of the analysis of tides based on the HHT method[J]. Journal of Tianjin University (Science and Technology), 2020(7): 725-735.
[68] KUKULKA T, JAY D A. Impacts of Columbia River discharge on salmonid habitat: 1. A nonstationary fluvial tide model[J]. Journal of Geophysical Research: Oceans, 2003, 108(9): 3293.
[69] KUKULKA T, JAY D A. Impacts of Columbia River discharge on salmonid habitat: 2. Changes in shallow-water habitat[J]. Journal of Geophysical Research: Oceans, 2003, 108(9): 3294.
[70] GAN M, CHEN Y, PAN S, et al. A modified nonstationary tidal harmonic analysis model for the Yangtze estuarine tides[J]. Journal of Atmospheric and Oceanic Technology, 2019, 36(4): 513-525.
[71] YU X, ZHANG W, HOITINK A J F. Impact of river discharge seasonality change on tidal duration asymmetry in the Yangtze River Estuary[J/OL]. Scientific Reports, 2020, 10(1): 6304[2020-09-09]. DOI: 10.1038/ s41598-020-62432-x.
[72] PAWLOWICZ R, BEARDSLEY B, LENTZ S. Classical tidal harmonic analysis including error estimates in MATLAB using TDE[J]. Computers and Geosciences, 2002, 28(8): 929-937.
[73] JIN G, PAN H, ZHANG Q, et al. Determination of harmonic parameters with temporal variations: An enhanced harmonic analysis algorithm and application to internal tidal currents in the South China Sea[J]. Journal of Atmospheric and Oceanic Technology, 2018, 35(7): 1375-1398.
[74] 樊伟. 海洋生态系统动力学数值模拟与同化研究[D]. 青岛: 中国海洋大学, 2009.
FAN Wei. Data assimilation and numerical study on a marine ecosystem model[D]. Qingdao: Ocean University of China, 2009.
[75] 李晓燕. 海洋生态系统动力学模型中控制参数时空分布的反演研究[D]. 青岛: 中国海洋大学, 2013.
LI Xiaoyan. Optimization of the spatio-temporal parameters in a dynamical marine ecosystem model based on the adjoint assimilation[D]. Qingdao: Ocean University of China, 2013.
[76] 王春晖. 海洋生态系统动力学模型伴随同化研究及应用[D]. 青岛: 中国海洋大学, 2013.
WANG Chunhui. Numerical study and application of a marine ecosystem dynamical model with adjoint assimilation method[D]. Qingdao: Ocean University of China, 2013.
[77] PAN H, LV X, WANG Y, et al. Exploration of tidal- fluvial interaction in the Columbia River Estuary using S_TIDE[J]. Journal of Geophysical Research: Oceans, 2018, 123(9): 6598-6619.
[78] DOODSON A T. The harmonic development of the tide-generating potential[J]. Proceedings of the Royal Society of London Series A, Containing Papers of a Mathematical and Physical Character, 1921, 100(704): 305-329.
[79] DOODSON A T. Perturbations of harmonic tidal constants[J]. Proceedings of the Royal Society of London Series A, Containing Papers of a Mathematical and Physical Character, 1924, 106(739): 513-526.
[80] DOODSON A T. VI. The analysis of tidal observations[J]. Philosophical Transactions of the Royal Society of London Series A, Containing Papers of a Mathematical or Physical Character, 1928, 227(647/658): 223-279.
[81] FOREMAN M G G, HENRY R F. The harmonic analysis of tidal model time series[J]. Advances in Water Resources, 1989, 12(3): 109-120.
[82] GODIN G. The analysis of tides[M]. Toronto: University of Toronto Press, 1972.
[83] MATTE P, SECRETAN Y, MORIN J. Temporal and spatial variability of tidal-fluvial dynamics in the St. Lawrence fluvial estuary: An application of nonstationary tidal harmonic analysis[J]. Journal of Geophysical Research C: Oceans, 2014, 119(9): 5724-5744.
[84] LEFFLER K E, JAY D A. Enhancing tidal harmonic analysis: Robust (hybrid L1 / L2) solutions[J]. Continental Shelf Research, 2009, 29(1): 78-88.
[85] MOFTAKHARI H R, JAY D A, TALKE S A, et al. A novel approach to flow estimation in tidal rivers[J]. Water Resources Research, 2013, 49(8): 4817-4832.
[86] MUNK W H, ZETLER B, GROVES G W. Tidal cusps[J]. Geophysical Journal of the Royal Astronomical Society, 1965, 10(2): 211-219.
[87] MATTE P, SECRETAN Y, MORIN J. Reconstruction of tidal discharges in the St. Lawrence Fluvial Estuary: the method of cubature revisited[J]. Journal of Geophysical Research: Oceans, 2018, 123(8): 5500-5524.
[88] MATTE P, SECRETAN Y, MORIN J. Drivers of residual and tidal flow variability in the St. Lawrence fluvial estuary: Influence on tidal wave propagation[J]. Continental Shelf Research, 2019, 174: 158-173.
[89] ZHANG F, SUN J, LIN B, et al. Seasonal hydrodynamic interactions between tidal waves and river flows in the Yangtze Estuary[J]. Journal of Marine Systems, 2018, 186: 17-28.
[90] CAI H, YANG Q, ZHANG Z, et al. Impact of river-tide dynamics on the temporal-spatial distribution of residual water level in the Pearl River channel networks[J]. Estuaries and Coasts, 2018, 41(7): 1885-1903.
[91] JAY D A, BORDE A B, DIEFENDERFER H L. Tidal-Fluvial and estuarine processes in the lower Columbia River: II. water level models, floodplain wetland inundation, and system zones[J]. Estuaries and Coasts, 2016, 39(5): 1299-1324.
[92] LU X, ZHANG J. Numerical study on spatially varying bottom friction coefficient of a 2D tidal model with adjoint method[J]. Continental Shelf Research, 2006, 26(16): 1905-1923.
[93] ZHANG J, LU X, WANG P, et al. Study on linear and nonlinear bottom friction parameterizations for regional tidal models using data assimilation[J]. Continental Shelf Research, 2011, 31(6): 555-573.
[94] GUO Z, PAN H, FAN W, et al. Application of surface spline interpolation in inversion of bottom friction coefficients[J]. Journal of Atmospheric and Oceanic Technology, 2017, 34(9): 2021-2028.
[95] GUO Z, PAN H, CAO A, et al. A harmonic analysis method adapted to capturing slow variations of tidal amplitudes and phases[J]. Continental Shelf Research, 2018, 164: 37-44.
[96] MALIK R, ZHOU F, CEDER G. Kinetics of non-equilibrium lithium incorporation in LiFePO4[J]. Nature Materials, 2011, 10(8): 587-590.
[97] ZONG X, PAN H, LIU Y, et al. Improved estimation of pollutant emission rate in an ocean pollutant diffusion model by the application of spline interpolation with the adjoint method[J]. Journal of Atmospheric and Oceanic Technology, 2018, 35(10): 1961-1975.
[98] PAN H, ZHENG Q, LV X. Temporal changes in the response of the nodal modulation of the M2 tide in the Gulf of Maine[J]. Continental Shelf Research, 2019, 186: 13-20.
[99] 方国洪, 潮汐分析和预报的准调和分潮方法, I. 准调和分潮[J]. 海洋科学集刊, 1974, 9: 1-15.
FANG Guohong. Quasi-harmonic constituent method for analysis and prediction of tides, I. Quasi-harmonic constituent[J]. Studia Marina Sinica, 1974, 9: 1-15.
[100] 方国洪, 潮汐分析和预报的准调和分潮方法, II. 短期观测的方法[J]. 海洋科学集刊, 1976, 11: 33-56.
FANG Guohong, Quasi-harmonic constituent method for analysis and prediction of tides, II. Methods for short-term observation[J]. Studia Marina Sinica, 1976, 11: 33-56.
[101] 方国洪. 潮汐分析和预报的准调和分潮方法, III. 潮汐和潮流分析的一个实际计算过程[J]. 海洋科学集刊, 1981, 18: 19-39.
FANG Guohong. Quasi-harmonic constituent method for analysis and prediction of tides, III. A practical calculation process for tidal and tidal current analysis[J]. Studia Marina Sinica, 1981, 18: 19-39.
[102] 陈宗镛. 潮汐学[M]. 北京: 科学出版社, 1980.
CHEN Zongyong. Tidal science[M]. Beijing: Science Press, 1980.
[103] 黄祖珂, 黄磊. 潮汐原理与计算[M]. 青岛: 中国海洋大学出版社, 2005.
HUANG Zuke, HUANG Lei. Tidal principle and calculation[M]. Qingdao: China Ocean University Press, 2005.
Review and prospect of tidal harmonic analysis method
LV Xian-qing1, 2, PAN Hai-dong1, 2, WANG Yu-zhe1, 2
(1. Physical Oceanography Laboratory, Ocean University of China, Qingdao 266100, China; 2. Pilot National Laboratory for Marine Science and Technology (Qingdao), Qingdao 266237, China)
As the most common physical process in the ocean, tides are closely related to economic development. Tidal harmonic analysis is the most widely used method for the analysis of tidal data. Since 1921, the tidal harmonic analysis model has gone through 100 years of development. This paper summarizes and reviews the research and development of tidal harmonic analysis in the past 100 years and forecasts its future development. It pays tribute to those who made achievements in the development and application of tidal harmonic analysis.
tide; harmonic analysis; amplitude; nonstationary tides
Sep. 10, 2020
P717
A
1000-3096(2021)11-0132-12
10.11759/hykx20200910003
2020-09-10;
2020-11-10
国家自然科学基金项目(42076011, U1806214); 国家科技计划项目(2019YFC1408405)
[National Natural Science Foundation of China, No. 42076011, No. U1806214; National Key Research and Development Plan of China, No. 2019YFC1408405]
吕咸青(1963—), 男, 山东青岛人, 教授, 主要从事物理海洋学研究, E-mail: xqinglv@ouc.edu.cn
(本文编辑: 丛培秀)
