基于势能信息熵的黄土小流域沟谷网络演化特征研究
2021-12-08赵卫东,周文怡,马雷,田剑,王淑琴
赵 卫 东,周 文 怡,马 雷,田 剑,王 淑 琴
(合肥工业大学资源与环境工程学院,安徽 合肥 230009)
0 引言
受内外应力等因素的长期作用,黄土高原地貌演化过程非常复杂[1-3]。沟谷网络是黄土高原流域地貌的主要侵蚀产沙区[4]和最主要的产沙运移通道,也是黄土小流域地貌系统研究中重要的地形因子,沟谷网络的演化过程很大程度上能反映其所属流域的地貌演化特征,因此,沟谷网络演化过程研究对探索流域地貌演化特征具有重要意义。以往沟谷网络研究多以黄土高原小流域为基本单元,借助室内模拟实验[5-8]、野外实际测量等数据,采用D8算法、多流向算法等提取沟谷网络[9-11],通过特征指标[12-15]对小流域地貌系统内部的沟谷网络形态等演化特征进行研究[16,17],流域内部沟谷网络的演化过程与整个流域系统地貌演化过程的相互作用机制未得到有效揭示,有待深入研究。
在一般系统论中,通常用有序和无序描述系统及系统内部各要素之间的状态和关系[18,19]。其中,有序在自然界和人类社会中存在静态有序(平衡结构)和动态有序(非平衡结构)[20]两种形式,现有研究表明,一个开放系统(如生物有机体等开放系统[21])可成为不断趋于有序化的系统。龚俊豪利用定量与定性相结合的方法,研究黄土高原小流域地貌系统的有序化演化机理,发现在以侵蚀为主的流域地貌系统的演化过程中,流域内部坡向和河网呈有序演化状态,初步阐明了以侵蚀为主的小流域地貌系统的演化过程是一个不断趋于有序化的过程[20]。然而,该研究仅从总体上对系统的河网有序性演化过程进行定性描述,未定量揭示河网具体的有序演化过程和有序程度。
熵能在一定程度上反映系统内部分子运动及能量的变化。近年来,部分学者在前人关于地貌熵研究成果[22-25]的基础上提出了新的地貌熵概念及计算方法。例如:Zhao等提出流域地貌熵的概念及计算方法,认为其与地貌的侵蚀发育紧密相关,并将流域地貌熵成功应用于黄土高原人工降雨小流域模拟试验中[26];姜琼在流域地貌系统和信息熵概念的基础上提出流域地貌系统势能信息熵的概念及计算方法,用于反映流域地貌系统内部势能分布的混乱程度,并对其蕴含的地貌演化意义进行初步研究,证明利用势能信息熵对流域地貌系统的地貌演化过程进行研究切实可行[27]。流域地貌系统作为开放的自然系统,其在演化过程中不断与外界产生物质交换和能量转换。例如,降雨通过入渗或地表径流进入流域地貌系统,降雨侵蚀会导致地表高程发生变化,从而使系统内部势能发生相应变化,因此,势能信息熵反映的系统内部势能在空间分布上的混乱程度可在一定程度上有效反映流域地貌系统内部的地貌侵蚀和演化发育特征。为此,本文拟以小流域地貌系统及其沟谷网络为研究对象,从势能信息熵角度定量研究流域地貌系统内部沟谷网络的有序演化过程。
1 数据与研究方法
1.1 研究数据
本文DEM数据来自人工模拟降雨条件下室内黄土侵蚀试验,模拟的黄土小流域长9.1 m,宽5.8 m,周长23.3 m,平均高差2.57 m,平均坡度15°;试验用土为陕西省咸阳市杨凌区附近的黑塿土,建模时分层填土,层层夯实,实测土体平均密度为1.39 g/cm3。利用近景数字摄影测量方法,获得该人工小流域地貌系统9期DEM数据(图1),相邻两期DEM的拍摄时间间隔为一星期左右,其中第1期为首次人工降雨前的初始地形,数据栅格单元大小为10 mm。该试验共经历23场不同强度、历时的降雨,总历时两个多月,9个侵蚀演变阶段的降雨参数如表1所示。
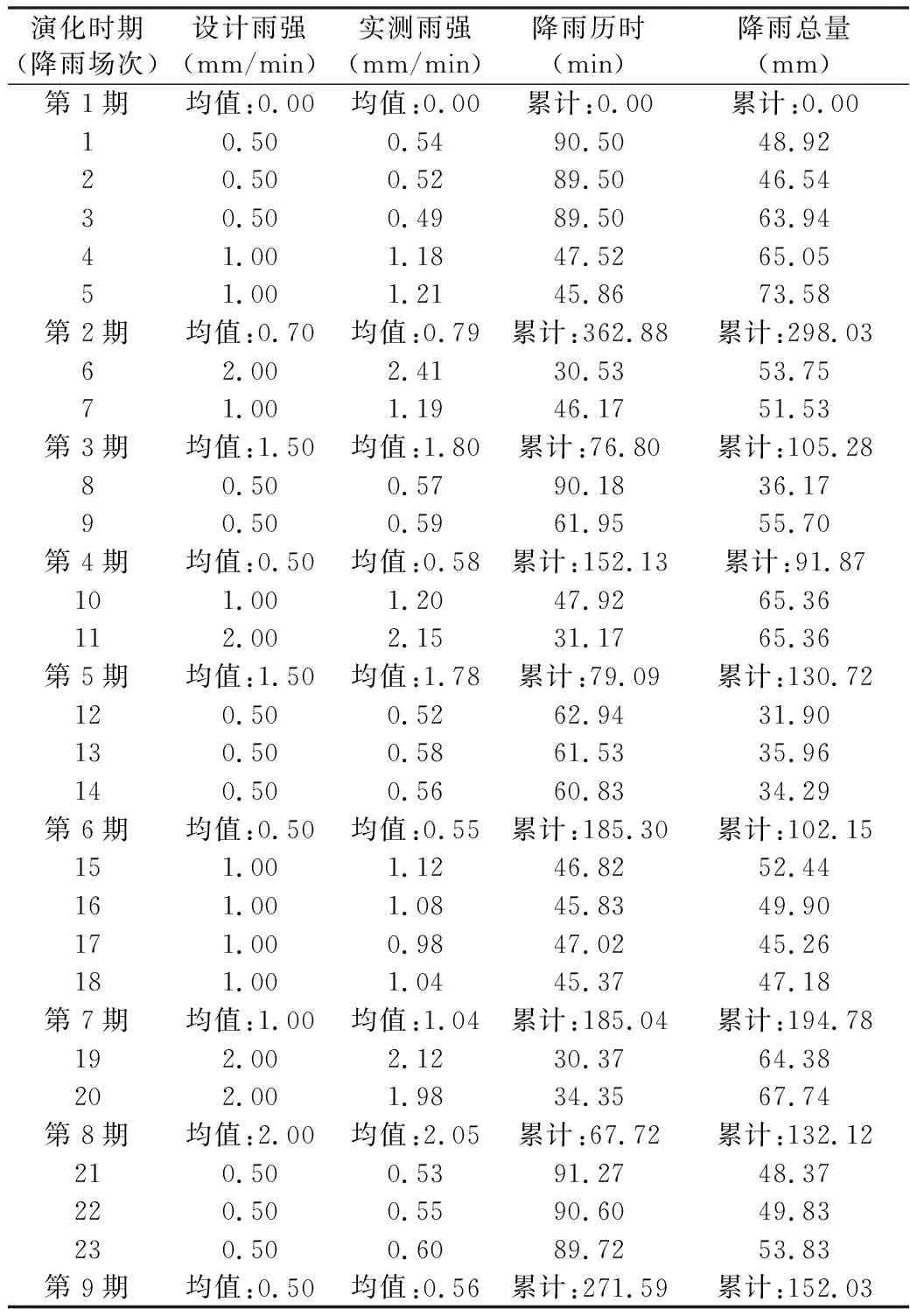
表1 室内人工降雨试验的降雨参数(根据文献[28]修改)Table 1 Parameters of indoor artificial simulated rainfall test (modified according to literature [28])
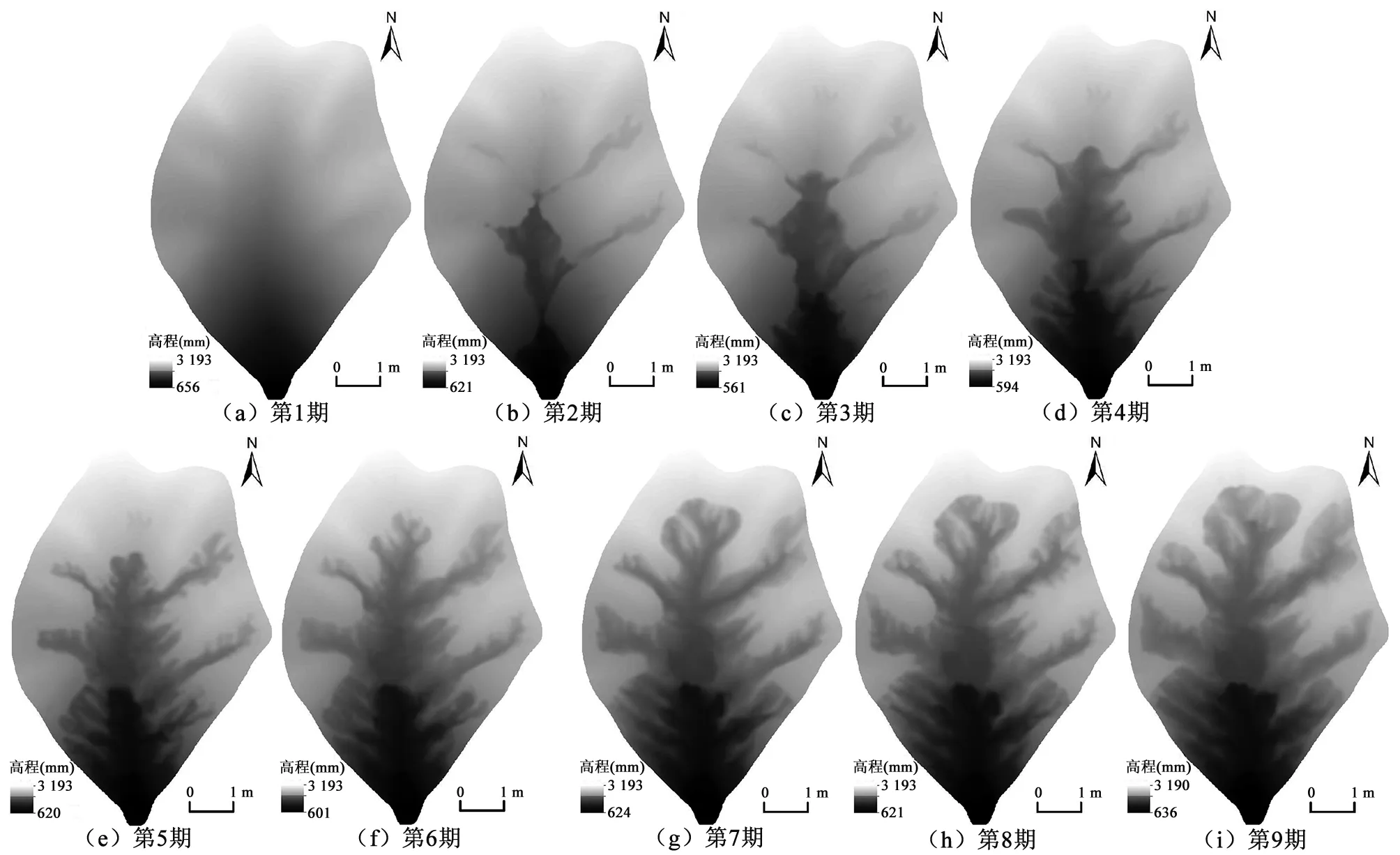
图1 室内人工降雨模拟的9期DEMFig.1 9-phase DEM of indoor artificial rainfall simulation
1.2 沟谷网络及子流域提取方法
首先,对9期DEM进行填洼处理,得到无洼地DEM;然后,利用D8算法计算水流方向,并根据水流方向数据得到每个单元格的汇流累积量;当该汇流累积量大于地表产生汇流所需汇流累积量的临界值时,该单元格就被识别为潜在水流路径,这些水流路径相互连接即构成整个沟谷网络。因此,合理确定地表产生汇流所需汇流累积量的临界值是准确提取沟谷网络的关键。本文采用南学良等[29]提出的沟谷网络密度二阶导函数参数确定汇流累积量的临界值,通过沟谷网络密度与阈值之间的关系得到其幂函数拟合方程,进一步得到其二阶导函数,能较好地排除阈值选取的主观性。本文9期小流域沟谷网络密度二阶导函数曲线如图2所示,可以看出,当汇流累积量阈值为8 000时,沟谷网络密度二阶导函数值趋近于0[30]。因此,本文取8 000为汇流累积量阈值,并在此基础上对提取的沟谷网络进行Shreve分级。
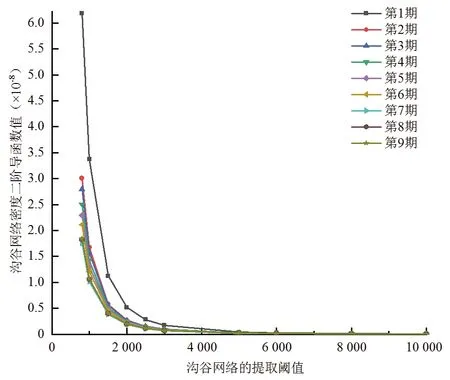
图2 沟谷网络密度二阶导函数曲线Fig.2 Curves for second order derivative of valley network density
1.3 势能信息熵计算方法
由于整个流域地貌系统的势能难以直接计算,因此,基于DEM格网剖分技术将流域划分为多个正方格网单元,后续流域地貌系统内部的势能及势能信息熵均基于上述剖分单元进行计算。由于本文流域地貌系统为室内人工模拟地貌系统,系统内部黄土密度均匀,因此不进行土层垂直方向上的剖分。流域地貌系统内部第i行和第j列剖分单元的势能Epi,j计算公式为[27]:
(1)
式中:ρ为黄土密度(1.39 g/cm3);g为重力加速度(10 N/kg);d为格网单元尺寸(10 mm);Hi,j为第i行第j列剖分单元相对于流域地貌系统出口最低点的高度(mm)。
假设某流域地貌系统内部共剖分出n个计算单元,利用式(1)可计算出每个单元的势能,从而得到该流域地貌系统的最大和最小势能,进而将系统势能等间距划分成N个势能等级,则该流域地貌系统的势能信息熵Hg计算公式为[27]:
(2)
式中:p(i)为单元i所属的势能等级在该流域中所有势能等级中出现的概率。
由式(2)可知,流域地貌系统的势能信息熵值与势能等级的划分紧密相关,势能信息熵总体上随势能分级数的增加不断减小,当势能分级数达到足够大时才能得到一个稳定势能信息熵[27]。只有在最佳势能分级数下,才能准确计算出流域地貌系统的唯一势能信息熵。因此,本文取势能信息熵的变化率为负万分之一时对应的分级数为最佳分级数(4 915级),由此计算势能信息熵作为该流域地貌系统的唯一势能信息熵,后续势能信息熵均采用该分级数进行计算。
2 结果分析
2.1 基于Shreve分级的沟谷网络演化特征
利用前述沟谷网络提取方法提取9期DEM的沟谷网络如图3(彩图见封2)所示,每条沟谷旁标注的数字为该沟谷所属的Shreve级别。可以看出,9期DEM小流域沟谷网络均具有典型的树状结构。为定量描述树状结构的有序性,本文提出以下沟谷网络有序性程度判定规则:当沟谷网络中存在的Shreve级别最多且主沟谷上各沟谷级别之间连续分布,即中间沟谷级别没有缺失时,判定此时的沟谷网络有序性最强;反之,如果沟谷级别有缺失,则判定其有序性较弱,沟谷级别缺失越多,有序性越差;当沟谷网络的有序性达到最强后,如果其主沟谷的最大沟谷级别不断减小,也判定其有序性受到破坏,有序性变弱。
从图3可以看出,第1期DEM最大沟谷级别为第12级(沟谷总数为8个),缺失级数为第4、第6、第7和第10级。由于该初始地形为尚未进行人工降雨的人工构筑地形,与自然条件下形成的沟谷网络有明显差异,根据前述沟谷网络有序性强弱的判定规则,此时的沟谷网络有序性最差。第2期DEM最大沟谷级别为第10级(沟谷总数为9个),缺失第6级。经过第一次人工降雨后,人工构筑的沟谷网络受降雨冲刷后逐步合并演化,使缺失的沟谷级别大幅减小,沟谷有序性大幅增强,初步具备自然形成的沟谷网络形态。到第6期时,最大沟谷级别为第13级,与沟谷总数(13个)均达到最大值,且沟谷级别完整、连续,此时沟谷系统的有序性最强。
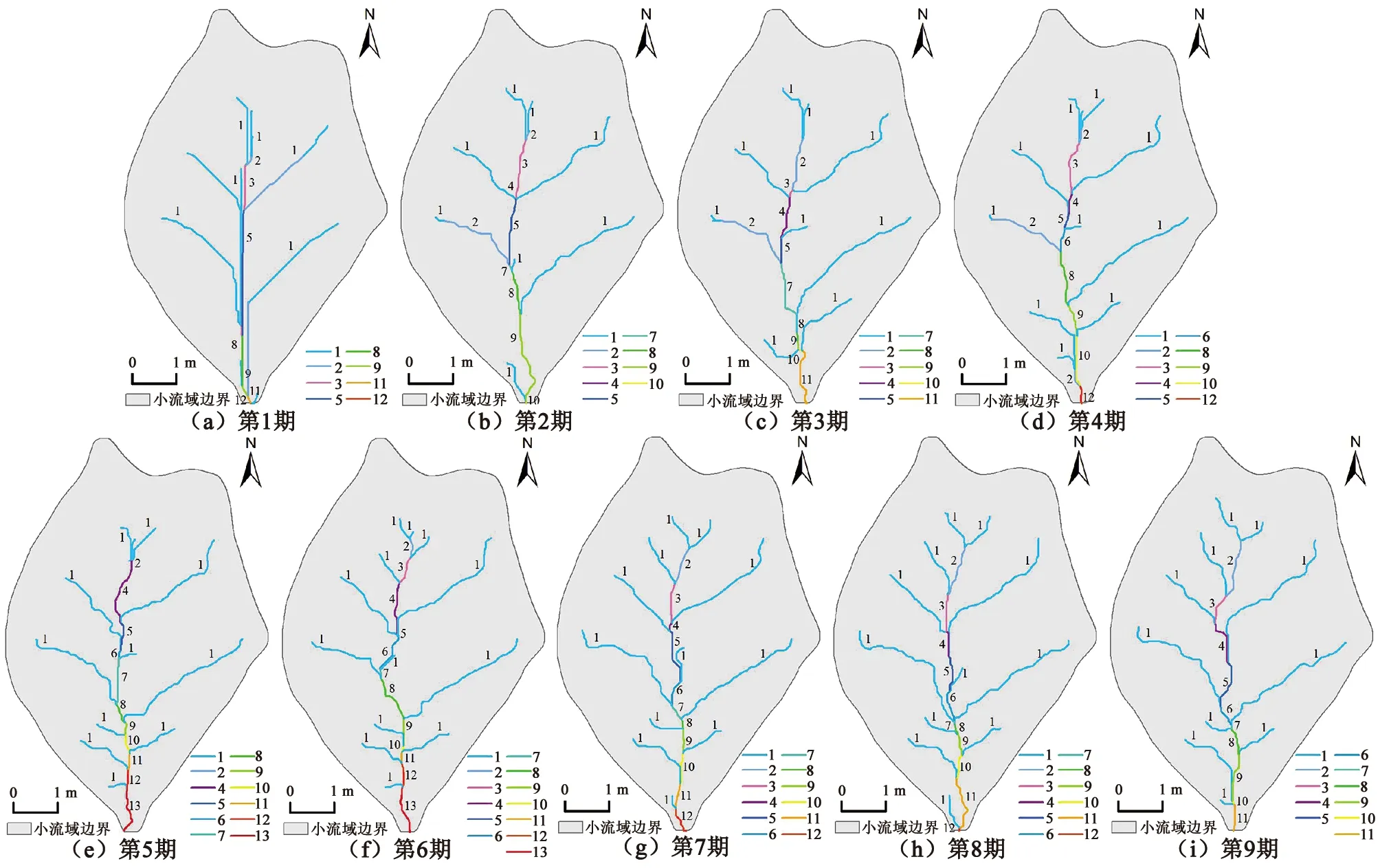
图3 提取的沟谷网络Fig.3 Extracted valley network
为进一步深入研究沟谷有序化演化过程,对9期DEM的沟谷级别总数和缺失数据进行统计(图4)可知,从第1期到第6期沟谷级别总数总体不断增加,主沟谷中缺失的沟谷级别整体不断减少,沟谷网络的有序化程度总体不断增强。其中,在从第3期到第4期的演化过程中,沟谷级别总数没变(均为10级),而缺失沟谷的级别却从1个增加到2个,表明该过程中沟谷网络的有序性遭到破坏,可能是由于第4期的降雨历时较长(是第3期的两倍多),导致流域出水口左侧的黄土出现塌陷和沟谷深切形成新支沟,从而破坏了沟谷网络的有序性。
从图4可知,第1期到第6期曲线总体从左上角向右下角延伸,将该阶段命名为第一阶段;第6期到第9期曲线从右向左延伸,将该阶段命名为第二阶段。在沟谷网络演化的第一阶段,虽然在不同程度上存在沟谷级别缺失的情况,但沟谷网络的最大级别数、级别总数不断增加,缺失的沟谷级别逐渐被补满,至第6期时沟谷级别总数达到最大(13级),且中间无缺失的沟谷级别,因此,总体上看,在沟谷网络演化的第一阶段,整个沟谷网络的有序演化程度不断加强。在沟谷网络演化的第二阶段,除主沟谷外,其他沟谷均无支流汇入,整个沟谷网络的沟谷级别完整,但主沟谷的最大沟谷级别数开始逐步减小,导致沟谷级别总数也同步减小,致使沟谷网络的有序性被破坏,沟谷网络的有序演化程度有所减弱。
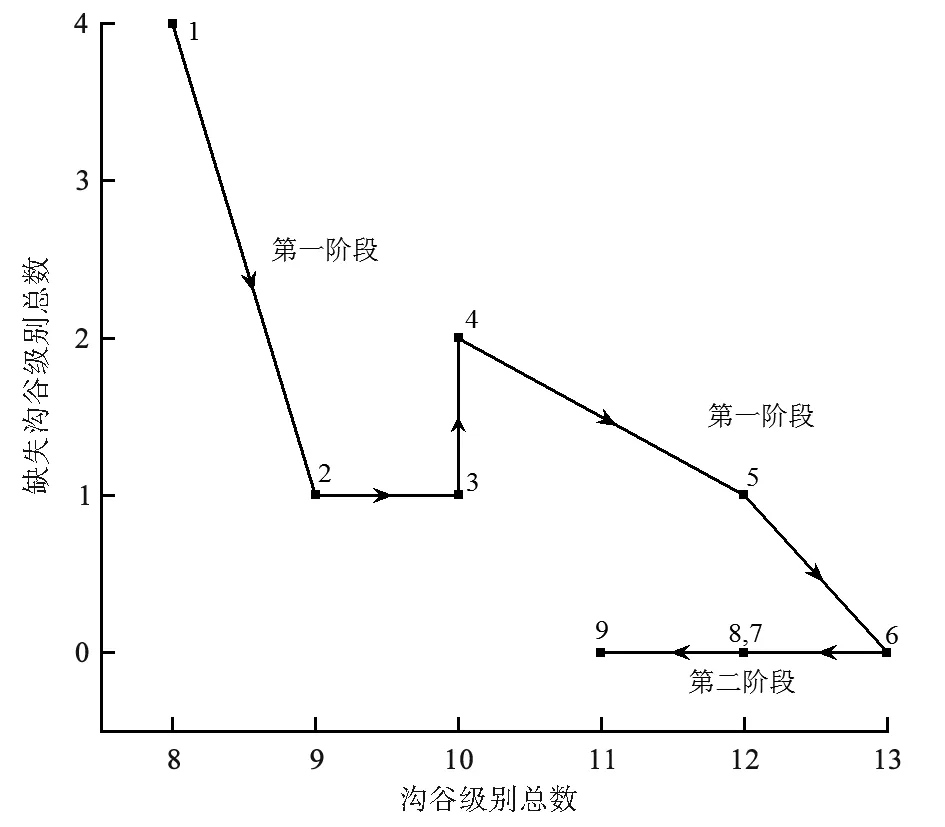
图4 沟谷级别总数与缺失沟谷级别总数的变化关系Fig.4 Relationship between the total number of valley levels and the total number of missing valley levels
2.2 基于势能信息熵的沟谷网络演化特征
由整个流域地貌系统的势能信息熵计算结果(图5)可知,9期DEM的势能信息熵均为负熵,且总体呈先递减后小幅增加的态势。根据文献[27],第1期到第6期为该小流域地貌演化的幼年期,流域地貌系统的势能信息熵从最大值-7.993逐步减小到第6期时的最小值-8.194,为势能信息熵的熵减过程;第6期到第9期为壮年期,势能信息熵从最小值-8.194小幅增至-8.147,为势能信息熵的熵增过程。根据一般系统论和熵变理论,开放系统的熵减过程为该系统有序化演化过程,熵越小,表明该系统的有序性越强,反之亦然。流域地貌系统是典型的开放系统,该系统在幼年期的地貌演化过程中有序化程度不断增强,但壮年期的地貌演化过程中有序化程度有所减弱,该结论与2.1节中流域地貌系统的沟谷网络有序演化过程完全一致。这表明,在以侵蚀为主的均质黄土流域地貌系统的演化过程中,地貌演化的幼年期是一个势能信息熵的熵减过程,同时也是该系统内部沟谷网络有序化程度不断增强的过程;壮年期则是一个势能信息熵的熵增过程,同时也是该系统内部沟谷网络有序化程度不断减弱的过程。在本文实验条件下,流域地貌系统势能信息熵的熵变规律及其内部沟谷网络的有序化程度均对流域地貌系统的地貌发育阶段具有良好的指示作用。
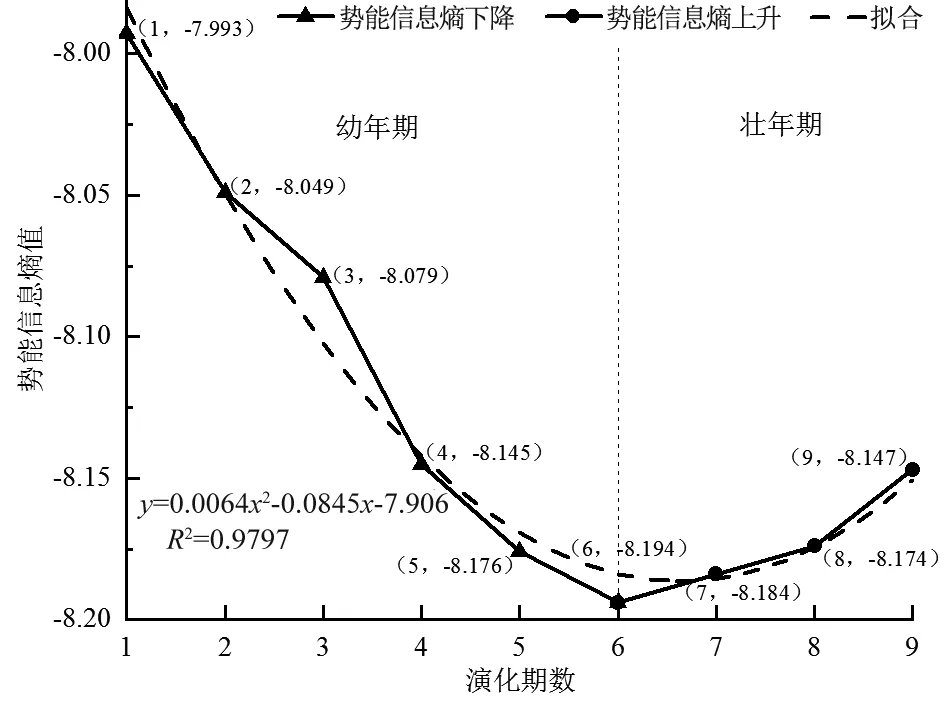
图5 9期黄土小流域总的势能信息熵值变化过程Fig.5 Changes of total PEIE values of small loess watershed in the 9 phases
3 结论与讨论
本文基于室内模拟人工降雨试验获取的均质黄土小流域地貌演化过程中的9期DEM数据,探讨了黄土小流域地貌系统内部的沟谷网络和势能信息熵的演化特征。首先,提出一种判别流域地貌系统内部沟谷网络有序程度的新规则,该规则能对沟谷网络的有序程度进行有效的定量表达。然后,计算整个流域系统的势能信息熵,结果表明:以侵蚀为主的均质黄土流域地貌系统在地貌演化的幼年期是一个势能信息熵的熵减过程,同时也是该系统内部沟谷网络有序化程度不断增强的过程;在地貌演化的壮年期则是一个势能信息熵的熵增过程,同时也是该系统内部沟谷网络有序化程度不断减弱的过程。势能信息熵的增减、沟谷网络有序化程度的强弱均与流域地貌的发育阶段相对应,因此,流域地貌系统势能信息熵的熵变规律及其内部沟谷网络的有序化程度均对流域地貌系统的地貌发育阶段具有良好的指示作用。
本文仅探讨了黄土小流域地貌系统演化过程中幼年期和壮年期早期的势能信息熵和沟谷网络的演化特征,之后的演化过程特征有待进一步深入研究。此外,后续室内模拟实验中应充分考虑土层的非均质性、植被等对流域系统地貌演化过程的影响。
