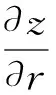磁流变抛光曲率效应的量化评价方法

杨 航,赵 功,贾 阳,何建国,黄 文

(1.遵义师范学院工学院,贵州 遵义 563006；2.中国工程物理研究院 机械制造工艺研究所,四川 绵阳 621900；3.华中光电技术研究所 武汉光电国家实验室,湖北 武汉 430073)

1 引 言

磁流变抛光技术作为具有革命性的超精密光学元件加工技术,被广泛应用于强激光系统光学元件最终修形[1-2],其工具特性使其能够有效控制低频、中频、高频面形,并能够对光学元件的亚表面损伤层进行有效的去除而不留下新的残余损伤[3-4]。磁流变抛光作为一种确定性抛光技术,其抛光过程的收敛效率和所能达到的极限修整精度依赖于工艺过程的确定性,如去除函数的确定性[5]、轨迹实现的确定性[6]、面形误差测量的确定性[7]、机床后置处理实现的确定性[8]等多方面的因素。

对于平面类光学元件的修整,不论光学晶体还是光学玻璃,磁流变抛光在各工艺环节已可以获得较好的确定性,达到可观的收敛效率和修整精度。然而,对于球面、非球面、自由曲面、柱面等具有曲率的光学元件,由于加工、测量等技术问题,其各工艺环节的确定性难以达到要求[9-12]。由于曲率的存在,其对磁流变抛光各工艺环节的影响机制不明确,也阻碍了收敛效率和极限精度的进一步提高。

张峰、Kordonski等人建立了光学元件曲率特征与去除函数形成的流动动力学模型[13-14]；Schinhaerl等人提出了抛光非球面镜面时缎带与光学元件的几何关系分析方法[15],可以用于分析不同曲率光学元件对浸入深度的影响规律；Seok等人研究了使用磁流变抛光在硅基微结构上制造曲面的方法,他们分析了不同曲率条件对磁流变抛光边缘效应的影响机制[16]；Guan等人基于lap-MRF研究了抛光区域缎带形成几何条件改变时材料去除率的理论模型[17]；Alam等人为克服凸和凹样品曲率的影响设计了特制的抛光工具实现了铜基曲面的加工[18-19]；宋辞等人建立了非球面抛光多轴联动、工件表面坐标系、机床坐标系的几何关系,为分析不同曲率光学元件加工运动量提供了理论方法[20]。王嘉琪、杨航等人从磁流变抛光液流场特性出发对抛光工具的不确定性对于抛光工艺参数集的依赖关系进行了理论分析与实验验证[21-23]。

在工程实践中,常把非平面类零件特性对抛光引入的不确定性称为“曲率效应”。然而,曲率效应的影响机制尚未得到有效的研究。本文将深入研究光学元件的曲率对磁流变抛光质量的影响规律。

2 曲面光学元件磁流变抛光工艺

2.1 曲面光学元件

光学元件种类繁杂,按照其几何外形可以分为平面类光学元件和非平面类光学元件。平面类光学元件可以认为是加工面曲率半径无穷大的面形,相应地非平面类光学元件则为加工面曲率半径为有限值。广义地,我们将所有具有有限曲率半径加工面的光学元件称为曲面光学元件。如图1所示。

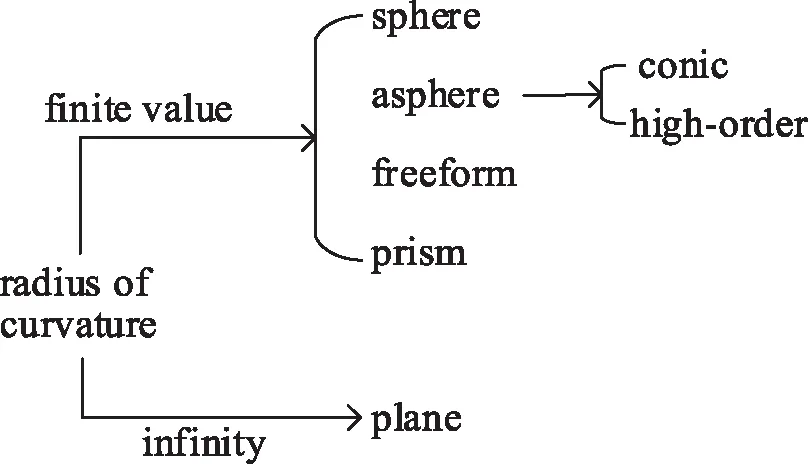
图1 曲面光学元件的分类Fig.1 Classification of curved optics

现有磁流变抛光工艺对于无穷大曲率光学元件具有较好的收敛效率和极限精度,然而当曲率半径具有有限值,特别是曲率半径较小时,磁流变抛光工艺的工艺受到不可预知的影响。本文将光学面形曲率对磁流变抛光工艺不确定性的影响称为曲率效应。

2.2 磁流变抛光原理

磁流变抛光利用磁流变抛光液(由基载液、羰基铁粉、氧化铈/金刚石粉颗粒以及其他添加剂组成)在梯度磁场下形成缎带实现对光学材料的微量去除,通常去除速率为～4λ/min。在抛光液流动方向,梯度磁场均匀分布；在缎带横断面方向,磁场具有类高斯分布；在光学元件法向,磁场以高梯度进行衰减。使得抛光液能够紧贴在抛光轮表面并随之旋转,在光学元件表面形成D形抛光斑。如图2所示。

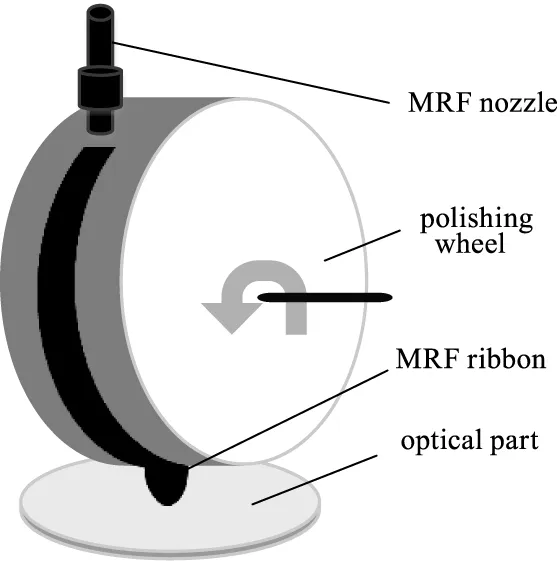
图2 磁流变抛光示意图Fig.2 Schematic diagram of magnetorheological finishing

对抛光斑进行干涉测量获得去除函数,去除函数即为对磁流变抛光工具影响的定量评价。抛光斑的大小与缎带和光学表面的几何关系密切相关,其深度(即去除量)与缎带在光学元件表面的驻留时间密切相关。单位时间内的去除量通常在同一工艺条件下保持稳定,这也是磁流变抛光实现确定性加工的基础。

3 曲率效应分析

3.1 磁流变抛光确定性对曲率效应的依赖关系

磁流变抛光抛光头在形成稳定缎带以后,对光学元件表面的误差去除量等于去除函数与驻留时间的卷积。因此,给定初始面形和去除函数,便可以确定获得最终面形。对光学面形的确定去除过程如图3所示。

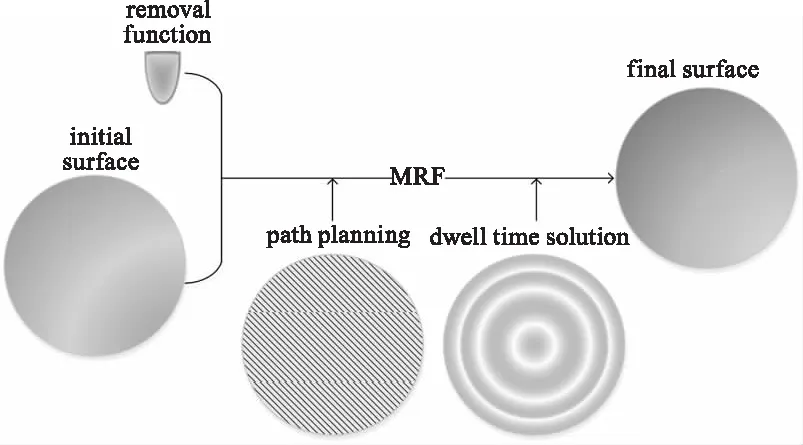
图3 磁流变抛光面形确定性控制过程Fig.3 Magnetorheological finishing surface shape deterministic control process

在对光学面形的确定性控制过程中,每一个环节引入的不确定性(或误差)均会使实际修形结果偏离预期修形结果,降低了面形控制过程的确定性。由光学面形曲率在各工艺环节引入的不确定性即曲率效应对抛光过程的影响。在面形测量环节、轨迹规划、去除函数获取、驻留时间求解、机床定位加工等环节均会引入由曲率效应导致的不确定性,这些不确定量均会使实际加工结果偏离预期加工结果。

3.2 曲面误差展开的曲率效应

由激光干涉仪测量获得的光学面形误差是磁流变抛光工艺规划的基础,其决定了元件表面每一点应当施加的去除量。然而激光干涉仪对光学元件表面的测量是离散的,其面形误差数据在垂直于口径方向是均匀分布的。这种测量的固有特性决定了当对平面元件进行干涉测量时,其面形误差也是均匀分布的。然而,当子孔径存在曲率时,垂直于孔径的均匀测量对于面形误差其实是不均匀的。这种情况下,当曲率较大时,实际的面形误差分布稠密程度会在严重降低。如图4所示。

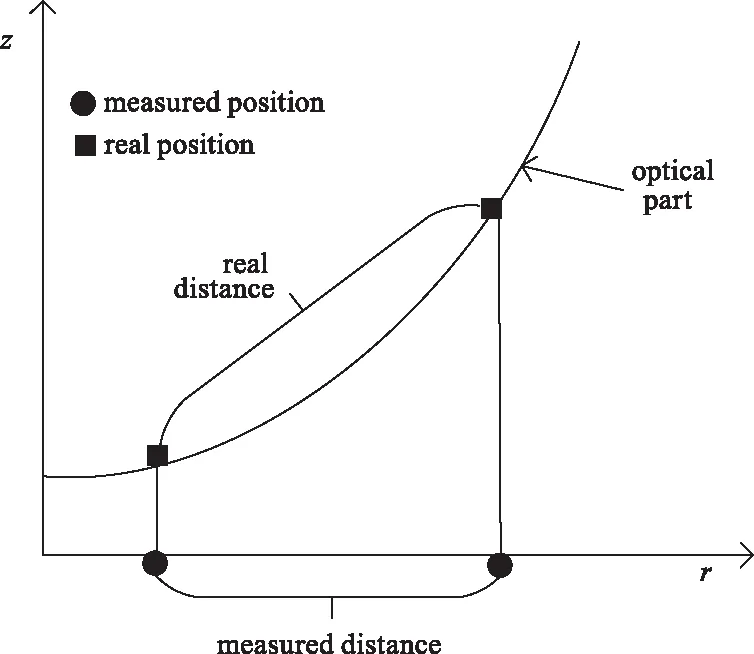
图4 面形误差展开的曲率效应Fig.4 Curvature effect of surface error expansion

光学曲面可以表示为:

不论对于x方向还是y方向,由于曲率效应的存在,两点之间的曲面距离均被拉长。设两点(x1,y1)和(x2,y2),则曲面距离s为:

对于x、y轴,由曲率导致的曲面距离分别为:

设x1、y1均为零,x2、y2为干涉仪测量获得的面形误差控制点的空间位置,则根据式(4)可以得到曲面误差点的实际空间分布。设干涉仪测量获得的面形误差分布为(x,y),则按照曲面展开后为:

(sx|x1=0,x2=x,y1=0,y2=y,sy|x1=0,x2=x,y1=0,y2=y)

3.3 轨迹规划的曲率效应

光学表面磁流变抛光采用的轨迹种类繁多,有光栅线、螺旋线、自适应轨迹、伪随机轨迹等等。对于大部分光学元件,特别是曲面光学元件的磁流变抛光,一般采用光栅线加工。设预设栅距为a、步进间距为b、光栅轨迹起点距离光轴距离为e。如图5所示。

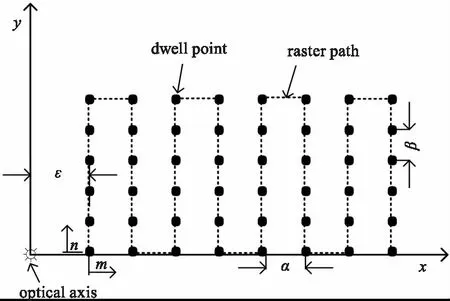
图5 光栅线轨迹加工示意图Fig.5 Schematic diagram of raster line trajectory processing

平面光栅轨迹的栅距和步进距离都是均匀分布的。当在子孔径内规划的光栅轨迹用于曲面加工时,曲面栅距和步进方向驻留点的曲面距离均会因为曲率效应而扭曲,与预设的驻留轨迹出现偏差。对于曲面S(c,k),由曲面效应导致的第m列栅距为:

sα(m)=sx|x1=ε+mα,x2=ε+(m+1)α,y1=y2=0,m=0,1,2,…

曲面效应影响下的第m列、第n个驻留点的步进间距为:

sβ(m,n)=sy|x1=x2=ε+mα,y1=nβ,y2=(n+1)β,m=0,1,2,…,n=0,1,2,…

由于光学曲面沿着光轴具有回转对称性,与坐标轴未对齐的轨迹规划可以等同于图5所示的与坐标对齐的轨迹规划而不会影响轨迹的几何性质。因此,式(5)和式(6)对任意曲面的光栅轨迹均适用。

3.4 去除函数获取的曲率效应

去除函数是磁流变抛光工具对工具表面去除效果的定量评价,需要对每一个驻留点的去除函数进行确定性获取。对于平面光学元件而言,所有驻留点处的几何条件都是一致的,在保证工艺参数稳定的情况下,对一个驻留点进行去除函数获取即可以获得所有驻留点的去除函数。然而,对于曲面,只有与光轴等距的圆周上的驻留点才有相同的几何条件。在子午平面内,任意两个点的几何条件都不会完全一样。

工程上采用具有相同几何性质和理化特性的样件进行采斑,用干涉仪对抛光斑测量进而获得去除函数。对于二次曲面、高次曲面,只能采用最接近球面(bfs)上的去除函数近似曲面各驻留点的去除函数。这种评价驻留点处去除函数的方式对于所有驻留点的去除函数评价都是不准确的,因为bfs与曲面的空间距离存在导致抛光液缎带的浸入深度相对实际减小了,而浸入深度对去除函数的形成至关重要。如图6所示。

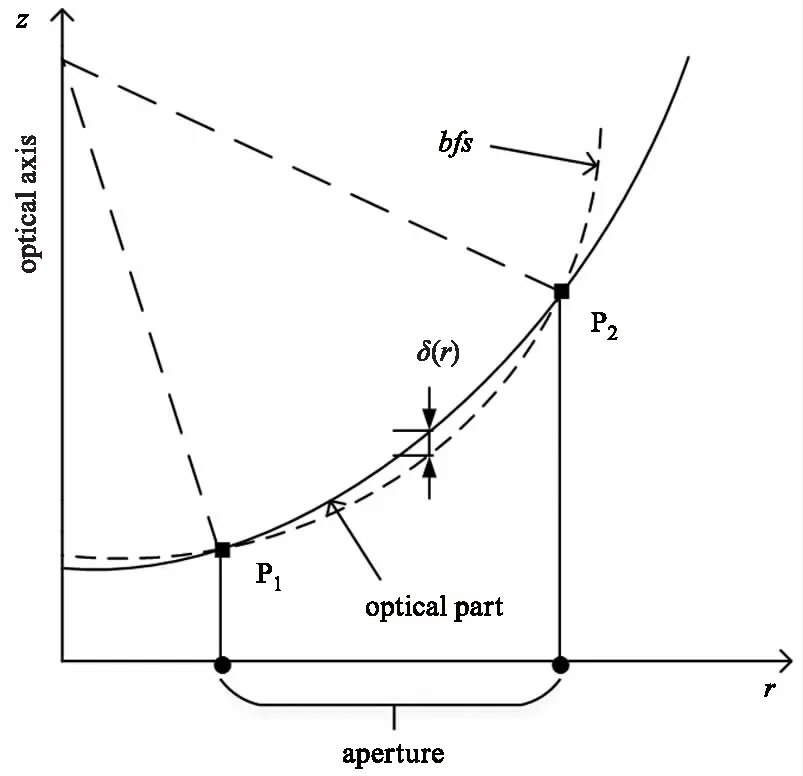
图6 曲面驻留点处去除函数形成的间隙变化情况Fig.6 Change in the gap by the removal function dwelling at the surface

不失一般性,对于二次曲面bfs与镜面的母线两个端点相交,设交点为P1(x1,z1)和P2(x2,z2),bfs的球心位于光轴上。则最接近球面sbfs(r)和曲面sa(r)的浸入深度的差值为:

δ(r)=sbfs(r)-sa(r)

其中,

根据式(7)可以对去除函数在各驻留点的浸入深度偏差进行评估,进而确定曲率效应对去除函数的影响。

3.5 驻留时间求解的曲率效应

作为一种子孔径柔性加工方法,磁流变抛光的抛光工具为D形去除函数。为获得确定的去除函数,需进行法向加工。对于平面光学元件,各驻留点处的法向量一致。对于曲面,各驻留点的法向量均指向光轴,因此,各驻留点法向量都不一样。进而由于曲率的存在,去除函数的分布与平面时也不一样,如图7所示。

图7 曲面与平面驻留点处去除函数分布形态差异Fig.7 Differences in the distribution of the removal function dwelling at the surface and the plane

可以看出,对于在轴曲面,去除函数的分布聚焦于几何中心；离轴曲面去除函数分布聚焦于光学口径外；对于平面,则可以认为聚焦于无穷远处。

磁流变抛光去除量分布函数是去除函数与驻留时间函数的二维卷积,卷积过程可以离散为:

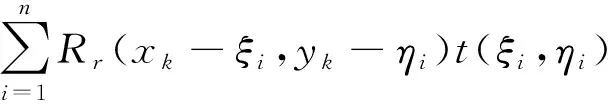
(k=1,2,…,m)

式中,m为面形控制点个数;n为轨迹上驻留点总个数。H(xk,yk)为光学元件(xk,yk)处的去除量；Rr(xk-xi,yk-hi)为去除函数驻留在(ξi,ηi)对点(xk,yk)处的材料去除量；t(ξi,ηi)为去除函数在轨迹点(ξi,ηi)处的驻留时间。表示成矩阵方程为:

Hm×1=Rrm×n×tn×1

其中,

根据式(10)可以采用数值方法求解驻留时间。曲面抛光的驻留时间求解过程与平面抛光不同之处在于计算去除函数影响矩阵Rr时需要加入去除函数聚焦引入旋转量的影响。Rr的各行向量的数值为对于确定的控制点,各轨迹点处去除函数对该控制点的影响。Rr的各列的数值为特定轨迹点去除函数对各控制点的影响。设去除函数的去除效率分布为F(x,y),其坐标系为O′-x′y′z′,如图8所示。

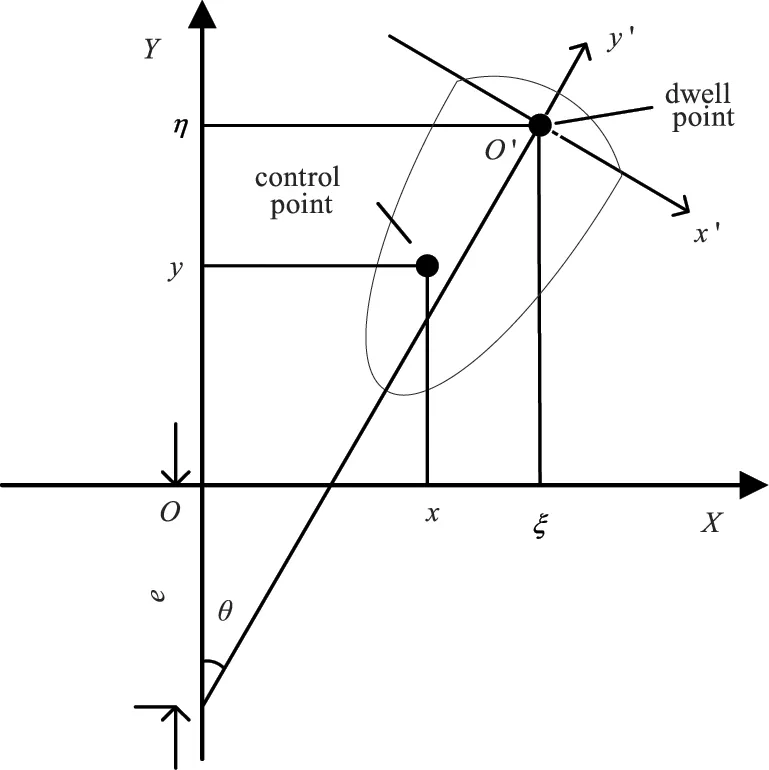
图8 曲率效应对去除函数的分布引入旋转量Fig.8 Curvature effect introduces the amount of rotation on the distribution of the removal function

设光轴中心的离轴量为e。没有旋转量时,位于(ξ,η)处的去除函数对(x,y)处的控制点的去除效率为F(x-ξ,y-η)。当去除函数有一个旋转角θ时,控制点在旋转后的轨迹点处的去除函数中的坐标为:

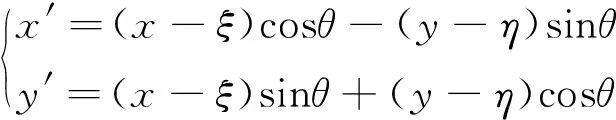
其中,

此时,控制点处的去除效率为F(x′,y′)。利用式可以定量评估曲率效应引入的去除函数分布变化,进而通过修正式中的Rr得到曲率影响条件下的驻留时间求解。

3.6 机床误差容错能力的曲率效应

磁流变抛光采用法向加工的加工模式,即抛光头在任一驻留点均要求与工件表面垂直。这一加工特点决定了法向浸入深度(简称浸深)是决定磁流变抛光精度的重要参数,浸深对磁流变抛光缎带与光学元件间的几何关系有着重要影响,关系到去除函数的可预测性与稳定性。而机床的法向定位精度对浸深的稳定性有着决定性的影响。设抛光头加工参考点坐标为xih=[x,y,z]h,在工件坐标系中对应的坐标为xiw=[x,y,z]w,则为满足法向加工的要求,存在一组机床工作轴运动量φ=(δx,δy,δz,δA,δB,δC)使得如下变换成立:

xiw=T(φ)·xih

可以看出,机床定位精度取决于f实现值的准确程度。当机床运动轴存在定位的静态误差或动态误差时,对浸深的影响可以表示为:

Δxiw=ΔT(φ)·xih

其中:

得到机床定位精度对浸深的影响规律后,可以进一步建立浸深误差对不同曲率光学元件的影响机制。设光学元件曲率半径为R,抛光缎带半径为Rr,抛光轮中心到工件曲率中心的距离为Rp。如图9所示。D为浸入深度,是工艺控制的法向几何参数；a0和b0分别为浸入长度和浸入厚度,表征光学元件切入缎带对去除函数形成的影响。

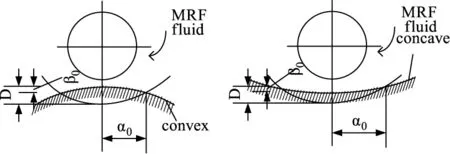
图9 凸面和凹面在磁流变抛光时的几何关系Fig.9 Geometric relationships of convex and concave surfaces during magnetorheological finishing

由几何关系可知,对于凸面:

Rp=R+Rr-D

对于凹面:

Rp=R-Rr+D

由海伦公式可以求得α0:

进一步可以得到b0:

根据式(15)、式(19)、式(20)可以定量评估曲率效应引起的机床误差容错能力的差异。不同曲率的工件在加工时对机床误差的误差容忍能力具有较大的差异。

4 结 论

磁流变抛光曲率光学元件时收敛效率和收敛精度很难达到同类平面光学元件抛光的水平。本文从磁流变抛光工艺过程出发,依据光学元件曲率对磁流变抛光各环节的影响规律建立了磁流变抛光曲率效应定量评价与分析理论。基于所建立的理论可以分析曲面误差展开、轨迹规划、去除函数获取、驻留时间求解以及机床误差容错能力等关键工艺环节的曲率影响机制。基于本文中的几何分析方法,可以进一步对曲率光学元件磁流变抛光工艺中的其他由曲率效应引起的工艺问题进行定量分析与评价。

附录:二次曲面的一阶导数

二次曲面为:

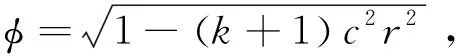
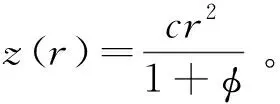
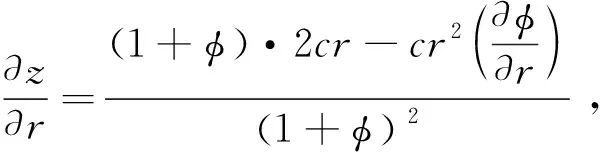
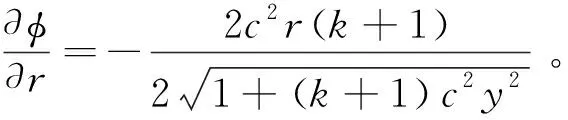
因此,