基于误差模型的结构光条纹周期数选择方法

刘 飞,严 谨,李佳鑫,杨时超,罗惠方,张茵楠

(重庆大学机械工程学院,重庆 400044)

1 引 言

相位测量轮廓术是获取物体形貌的一种重要方法[1]。在相位测量轮廓术测量过程中,首先利用投影仪向被测物体表面主动投影具有一定规律的编码图像,如条纹光栅等。再通过拍摄系统拍摄经物体高度调制后的变形条纹图像,并利用对应的相位展开技术求解物体高度信息。投影编码图像的特性会对相位测量轮廓术精度造成较大影响,其中条纹周期数是重要影响因素之一[2-3]。Huntley[2]通过推导说明条纹周期数的增加可以有效抑制相位误差,但并不能无限增加。基于Huntley等人的研究,杜宪[3]等通过假设法选取十组条纹周期数进行实验,选出其中一组条纹周期数作为最优条纹周期数,但并未系统给出条纹周期数选择方法的公式推导与理论模型。Li[4]等通过理论分析,在基于投影仪的非线性响应以及离焦效应的基础上,推导了相位误差模型以及三步相移法中的最大相位误差计算方法,提高了三维测量精度,但并未考虑条纹周期数对于测量精度的影响。

虽然国内外学者对条纹周期数对于相位测量轮廓术精度的影响进行了各自的研究,但基本上仍是基于经验、试凑等定性的方法,对于定量选择最优条纹周期数的方法仍比较欠缺。为减小三维重建误差,提高测量精度,本文基于上述问题提出一种基于误差模型的相位测量轮廓术条纹周期数定量选择方法。首先考虑影响相位测量轮廓术测量精度的主要因素,建立综合相位误差模型,计算最大相位误差；其次在基于多频外差的相位展开算法中,推导条纹周期数与最大相位误差的约束关系,利用约束方程与最大相位误差的关系,估计出合适的条纹周期数；最后通过仿真以及实验证明了本文提出的相位测量轮廓术条纹周期数定量选择方法能够有效的降低三维重建误差。本文提出的方法能实现相位测量轮廓术最优条纹数的定量选择,将促进相位测量轮廓术的发展与应用。

2 相位误差模型与条纹周期数约束方程

2.1 相位误差模型

相位测量轮廓术采用相移技术,通过一系列有一定相位差的条纹光栅进行相位解调。以条纹光栅横向分辨率W为1024 pixel为例,其中λ为条纹光栅中单个周期所包含的像素点个数,因此条纹周期数K=W/λ,由图1可知,条纹周期数K为6。

图1 条纹光栅Fig.1 Fringe pattern

当投影仪将条纹光栅投影至被测物表面,投射的标准N步相移法灰度分布函数为[5]:

In(x,y)=IA+IBcos[φ(x,y)-δn]

(1)

其中,In(x,y)为编码的理想条纹光栅的灰度分布函数;IA为整幅条纹光栅的平均灰度值;IB为整幅条纹光栅的调制灰度值;φ(x,y)为绝对相位;δn=2π×n/N为第n幅条纹光栅的相移,n=0,1,2,…N-1。

对应的条纹光栅包裹相位φ(x,y)为:

(2)

在相位测量轮廓术中,测量精度受到多方面的影响。通常相位误差主要来源可分为三种:光栅图像A/D转换的离散误差[3,6],投影仪的非线性响应误差[4,7-10],投影仪的离焦效应误差[4,11-13]。采用标准N步相移法时,其相位误差Δφ为[4]:

(3)

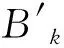
(4)

其中,α∈[0,1]为被测物体表面反射率;Bk为未考虑离焦效应时的k次谐波项系数,可由傅里叶变换求得[4]。T(f)为高斯离焦模型光学传递函数,f=K/W为条纹光栅的频率,K为条纹周期数,W为条纹光栅横向分辨率。

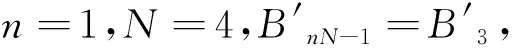
(5)

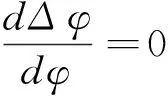
(6)

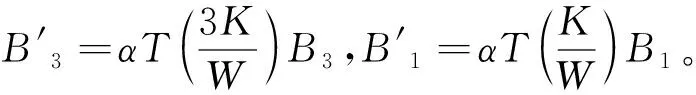
2.2 条纹周期数约束方程

基于多频外差原理的相位解包裹方法因其测量精度较高而应用较广[15-16]。本文在基于多频外差的全频解相方法上推导条纹周期数与相位误差的约束关系。由于使用标准三频四步相移法求解的包裹相位存在四倍频相位误差,因此,为保证绝对相位无跳跃性误差,需要满足如下约束[5]:

(7)

其中,K1、K2、K3为最高频、次高频、最低频的条纹周期数,即:K1>K2>K3。Δφmax为整幅条纹光栅中的最大相位误差,该误差与条纹节距大小无关[5,17]。因此最高频光栅1、次高频光栅2和最低频光栅3的最大相位误差均为Δφmax。

2.3 条纹周期数与相位误差对测量精度的影响

在结构光测量系统中,设某空间三维点的坐标为(Xw,Yw,Zw),则三维坐标计算公式为:

(8)

其中,sc,sp分别是相机和投影仪的比例因子。(uc,vc)和(up,vp)是相机和投影仪的图像坐标,Ac,Ap分别为相机和投影仪的内部参数,Mc,Mp分别为相机和投影仪的外部参数。

该点对应的投影仪图像坐标up可表示为:

(9)

其中,φ(uc,vc)为该点的绝对相位值;K为条纹光栅的条纹周期数;W为条纹光栅横向分辨率。

因此,在其他测量环境不变的情况下,投影仪图像坐标误差Δup可表示为[14]:

(10)

由式(8)可知,三维坐标的计算与投影仪图像坐标up有关,投影仪图像坐标误差Δup将会引起三维重建误差。由式(10)可知,当增加条纹光栅的条纹周期数K或者降低相位误差Δφ时,投影仪图像坐标误差Δup均将减小,因此三维重建误差也将减小。

由式(7)可知,K的选择与Δφmax直接相关,因此综合考虑条纹周期数K与相位误差Δφ对于Δup影响。在K1满足式(7)的约束条件下,K1取得最大值时,投影仪图像坐标误差Δup最小,此时K1的取值即为最优的最高频条纹周期数。

3 仿真与实验

采用标准三频四步相移法,使用MATLAB生成1024 pixel×768 pixel分辨率的条纹光栅进行仿真。基于常用实验环境的基础上,在生成的条纹光栅上添加T(f)值为0.886的离焦效应。选取条纹光栅平均灰度值IA=135,条纹光栅调制灰度值IB=85。在经过γ预畸变校正的基础上,使用MATLAB生成最高频条纹周期数K1从10～200的条纹光栅进行仿真。

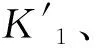
(11)

由式(7)可知,Δφmax与K直接相关。将Δφmax代入式(11),计算得到式(12):

(12)

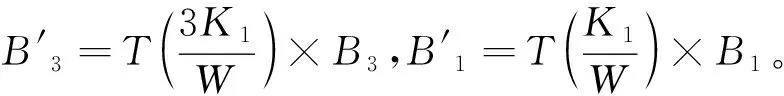
图2 仿真条件下最优条纹周期数计算Fig.2 Calculation of the optimal number of fringe periods under simulation conditions

为更进一步验证本文方法的有效性,使用型号为Acer H7850的投影仪,投影分辨率为1024 pixel×768 pixel的条纹光栅进行实验。使用单个AVT的CCD相机进行拍摄,相机型号为Manta-G505B,相机分辨率为2452 pixel×2056 pixel。采用标准三频四步相移法。调整标准平板与投影仪之间的距离和焦距,离焦效应光学传递函数T(f)最终调整结果的概率最大值为0.886。令条纹光栅平均灰度值IA=135,条纹光栅调制灰度值IB=85,在经过γ预畸变校正的基础上,使用MATLAB生成最高频条纹周期数从100～150的条纹光栅进行实验。

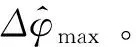
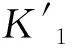
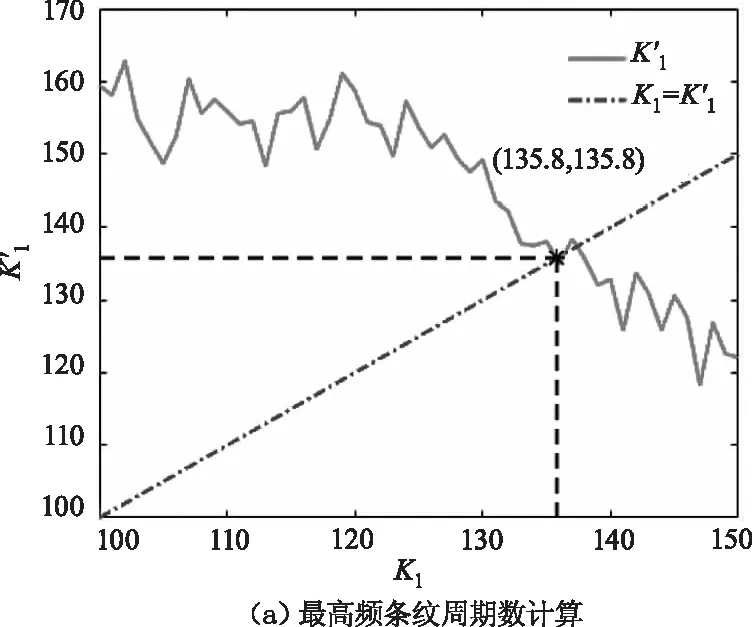
图3 实验条件下最优条纹周期数计算Fig.3 Calculation of the optimal number of fringe periods under experimental conditions

4 分析与讨论

为验证上述选择的条纹周期数是否合理且检测本文方法的测量精度,本文选择四组不同的条纹周期数进行对比实验。第一组为常用的最高频、次高频、最低频分别为70、64、59[14]的条纹周期数；第二组为最高频、次高频、最低频分别为126、120、115的条纹周期数；第三组为经本文方法优化后的最高频、次高频、最低频分别为136、130、125的条纹周期数；第四组为最高频、次高频、最低频分别为146、140、135的条纹周期数。利用标定好的结构光三维测量系统,采用标准三频四步相移法进行测量,根据标定数据解算三维点云。

使用标准平板进行实验,在解算出标准平板的三维点云后,对比分析点云数据封装结果和点云数据最佳平面拟合结果的最大偏差和标准差,其数值如表1所示。

表1 标准平板的重建误差分类Tab.1 Standard plate reconstruction error details

由表1可知,与第一组条纹周期数(传统方法)相比,第二组、第三组(本文优化方法)以及第四组条纹周期数实验结果中的正、负向最大误差以及标准差均低于第一组条纹周期数的正、负向最大误差以及标准差。其中,第三组条纹周期数实验结果中的标准差相较于第一组条纹周期数实验结果中的标准差,降低了44.4 %。

分析第二组、第三组以及第四组实验的条纹周期数可知,三组实验的条纹周期数相近。而应用了本文优化方法之后的第三组条纹周期数,实验结果中的正、负向最大误差以及标准差均为三组条纹周期数实验结果中的最小值。

5 结 论

为了提高相位测量轮廓术的测量精度,本文提出了基于误差模型的相位测量轮廓术条纹周期数优化方法。首先建立相位测量轮廓术误差模型,通过误差模型计算出最大相位误差。其次推导出最大相位误差与条纹周期数之间的约束关系。最后根据最大相位误差与条纹周期数的约束关系,求解最优条纹周期数。实验表明,本文所选取优化后条纹周期数对比传统方法条纹周期数的正、负向最大误差以及标准偏差均有明显下降。且经本文优化后的条纹周期数,在与其相邻的条纹周期数中的正、负向最大误差以及标准偏差均为最小值。因此,本文所提方法能够有效地求解相位测量轮廓术中所投影条纹光栅的最优条纹周期数,并提高相位测量轮廓术的测量精度。