基于k-means分簇和灰狼优化的无线传感网络路由算法

富立琪，王华倩，乔学工

（1.太原理工大学信息与计算机学院，山西晋中 030600；2.国网北京昌平供电公司，北京 102200）

无线传感网络(Wireless Sensor Networks,WSN)集成了传感器技术、计算机技术和无线通信技术等多方面技术，是目前学术界研究的热点之一[1]。由于传感器节点的能量有限且无法更换，因此延长传感器节点和整个网络生存时间成为了当前领域中的一个热门研究课题。

文献[2]中提出的算法由于将监测区域中的节点采用贪心算法形成地理位置上的链，并进行数据融合和传输，因此该算法较为复杂，存在网络负载不均衡的问题。文献[3]采用簇半径动态确定方式，将监测区域划分成不同的簇，该算法并未解决簇首分布不均匀的问题，造成节点过早死亡。文献[4]和文献[5]分别对簇首选择的方式和数据传输路径进行了改进，但都未考虑节点与汇聚节点的距离，导致部分节点过早死亡，网络负载不均衡。文献[6]虽使用了遗传算法选择最优路径进行传输，但该算法计算冗余，计算时延大。文献[7]将监测区域划分为4个象限，将节点能量和与汇聚节点的距离作为在LEACH 协议上改进簇首选择的重要因素。文献[8]采用k-means 算法划分簇，并引入休眠机制。但由于k-means 算法形成的簇分布不均匀，会有节点能量消耗过快的问题产生。文献[9]中采用了聚类评估指标优化簇首数量，该算法在簇首选举时未考虑节点位置，会导致簇首节点由于能量消耗过快而过早死亡。文献[10]中提出了k-means 分簇路由算法（KEAC），但“热区”的问题较为严重。为了改进上述算法的不足，文中提出了一种基于k-means分簇和灰狼优化的无线传感网络路由算法，该算法引入基于节点的位置和分布密度两个因素的竞争半径模型，优化k-means 算法形成的簇，并用改进灰狼优化算法在优化后的簇区域中选取簇首，监测区域内的节点将采用簇内单跳、簇间多跳的传输方式将数据发送给汇聚节点。文中使用Matlab对LEACH协议、KEAC 协议以及提出的算法进行仿真，结果表明，改进后的路由算法在延长网络的生存时间上有明显提高。

1 网络模型

在M×M的监测区域内，m个传感器节点随机分布，且节点部署后不会移动，每个节点具有相同且有限的能量和唯一的ID；汇聚节点在监测区域外，具有固定的位置和无限能量。监测区域内的每个节点具有一样的接收、发送和数据处理能力，可感知自己的位置信息；下一跳节点限定在靠近汇聚节点的区域内。

文中引用经典的一阶无线电模型[11-12]来计算节点的通信能耗，当传输距离为d时，节点发送lbit 数据所要消耗的能量如式（1）所示：

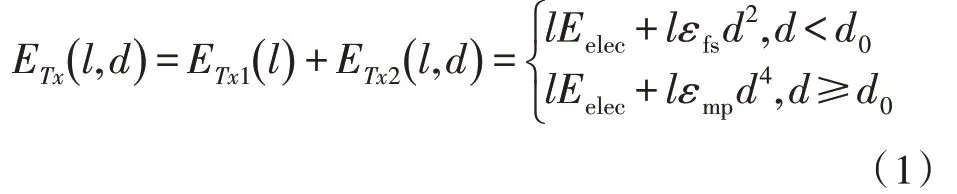
式（1）中，Eelec为发射电路中的能耗，εfs为自由空间模型功率放大能耗，εmp为多径衰减模型功率放大能耗[13]，两个参数的距离转换阈值为

节点接收lbit 数据所要消耗的能量如式（2）所示：

2 改进灰狼优化算法

灰狼优化算法（GWO）具有结构简单、需要调节的参数少、收敛性能较强、容易实现等优势[14]。算法将灰狼社会进行数学建模，最优解定义为α狼，优解定义为β狼，次优解定义为δ狼，其余的解定义为χ狼。狩猎时灰狼群体接近并包围猎物，其表达式为：

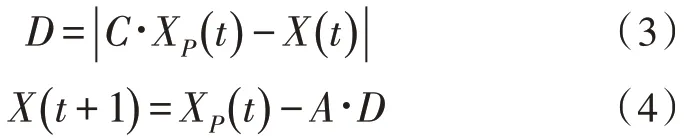
式（3）和式（4）中，t表示当前迭代次数，XP(t)是猎物位置，X(t)是灰狼位置，D表示灰狼与猎物的距离，A和C为系数，分别由式（5）和式（6）计算求出：

r1和r2是[0,1]之间的随机数；收敛因子a随迭代次数从2 减小到0。参数C的随机选取避免了算法陷入局部最优，提高了整个迭代过程中的全局搜索能力。在追捕猎物阶段，算法进行迭代并不断更新α狼、β狼及δ狼的位置，同时强迫其他灰狼个体更新位置，逐渐逼近猎物，因此，χ狼根据α狼的当前位置Xα、β狼的当前位置Xβ、δ狼的当前位置Xδ来更新各自的位置，式（7）表示χ狼朝α、β、δ狼前进的步长和方向，式（8）为χ狼的最终位置：

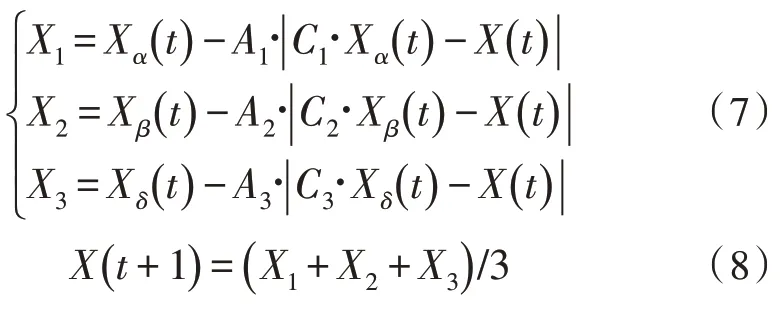
在包围攻击阶段时，灰狼群体逐渐向猎物靠近，随着迭代次数的增大，收敛因子a线性减小，A的值也随着a的减小而减小，当 |A|≤1 时，灰狼群向着猎物攻击，以实现局部搜索，当|A|>1 时，灰狼会进行全局搜索。

由于灰狼优化算法在搜索过程中是非线性变化的，而在迭代过程中收敛因子a是线性递减的，与算法的实际搜索过程不符合，同时文中要求算法在局部开发时能够有较强的收敛精度，所以为了提高算法后期局部的开发能力，并有效提高算法的全局探索和局部开发平衡能力，文中改进了一种基于非线性动态变化收敛因子的更新公式，如式（9）所示：

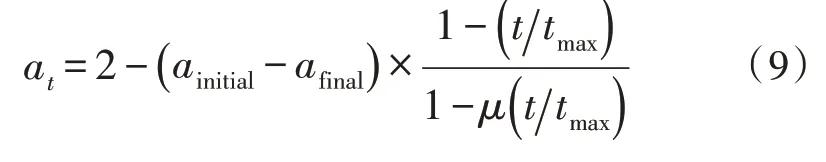
式（9）中，ainitial和afinal分别为a的初始值和终值，t为当前迭代次数，tmax为最大迭代次数，μ为非线性调制指数，文中μ取1.1。在整个迭代过程中，调整参数a的自适应值来平衡灰狼算法的全局探索和局部开发能力，加强后期的局部开发能力。由于改进后的灰狼优化算法提高了局部搜索能力，因此在利用改进后的灰狼优化算法对簇首进行选举时，选举簇首更加准确快速，进而延长了网络的生存周期。

3 基于k-means分簇和灰狼优化的路由算法

文中提出的路由算法主要分为3 个阶段：第一阶段为k-means 分簇优化阶段，根据节点与汇聚节点的距离和节点密度两个因素来优化k-means 聚类后所形成的簇结构，使得靠近汇聚节点的簇区域较小，避免“热区”问题的产生；第二阶段为簇首选举阶段，利用改进灰狼优化算法在各簇区域内进行簇首的选择，均衡网络负载；第三阶段为数据传输阶段，簇内节点以单跳的传输方式向簇首发送数据，簇首以多跳的传输方式汇聚节点发送数据，从而均衡网络能耗。

3.1 k-means分簇

1）k-means 算法分簇时首先给定一个k值，即划分的簇的数量，然后在每个簇中选举一个簇首节点。为了降低整个网络能耗，文中采取文献[15]和文献[16]方法确定最佳簇首数量。假设m个节点随机分布在M×M的监测区域内，监测区域被划分为k个簇，其中一个簇有mi（1 ≤i≤k）个节点，包含一个簇首节点和mi-1 个普通节点，汇聚节点位置距离监测区域较远。根据上述网络能耗模型计算簇首数目的最佳值。簇内节点通过单跳向簇首发送数据所消耗的能量为：

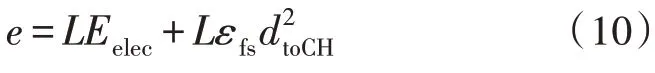
式（10）中，L为数据包大小，dtoCH是簇内节点到簇首节点距离的期望值；

簇首接收簇内节点数据，将数据融合后传输给汇聚节点所消耗的能量为：

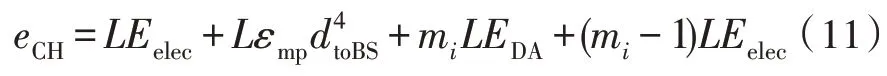
式（11）中，dtoBS是簇首节点到汇聚节点距离的期望值，EDA是节点融合1 bit 数据所消耗的能量，mi是簇内节点数。整个网络节点在一轮中所消耗的总能量为：

式（12）中，N（1 ≤N≤m）为当前轮数的存活节点个数。

对式（12）求解k的偏导数，可以得到最低能耗时的k值，即=0，最佳的簇首数量为：

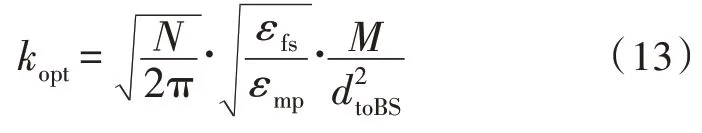
2）根据式（13）求出的最佳簇首数量，令k=kopt，即汇聚节点从m个节点对象中随机选择k个节点作为初始聚类中心，计算其他非聚类中心的节点与每个聚类中心的距离，并将节点分配到距离聚类中心最近的簇中。

3）节点分配完毕后，用式（14）重新计算每个簇中所有节点的质心；第i个簇中的质心表示为centeri(xi,yi)。

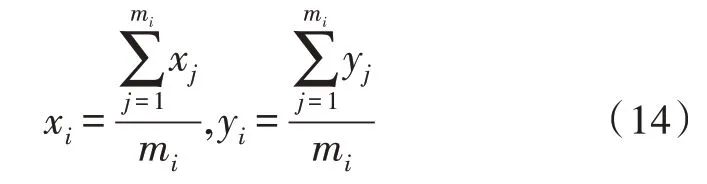
式（14）中的xj、yj分别为节点j的横坐标和纵坐标。

4）重复步骤2）和3），直到每次计算出来的质心与原来质心的距离小于设置的阈值（设为0.01）时算法结束，将此时的簇作为初始形成的簇。

由于k-means 算法形成的簇分布不均匀，而且靠近汇聚节点的簇可能会有“热区”的问题存在，导致簇首节点过早死亡。为了避免这些问题，文中将引入非均匀竞争半径对初始形成的簇进行优化，使得距离汇聚节点近的簇具有的竞争半径较小，距离汇聚节点远的簇具有的竞争半径较大，簇内的节点数也较少，均衡节点能耗，从而延长网络生命周期。第i个簇质心centeri的竞争半径为Ri：

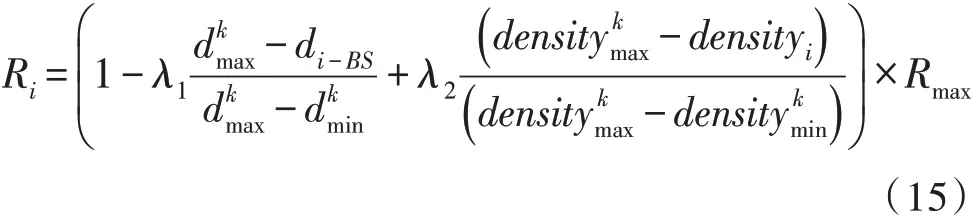
式（15）中的Rmax为最大竞争半径，和为分别为k个簇的质心到汇聚节点距离的最大值和最小值，di-BS为第i个簇的质心到汇聚节点的距离，λ1、λ2为权重，取值在[0,1]之 间。和分别为k个簇内节点密度的最大值和最小值，densityi为第i个簇内密度。

第i个簇内的簇质心竞争半径内的节点数为mRi，竞争半径内节点满足的条件为表示第i个簇中第j个节点到簇质心的距离，当<φ时，该簇存在“热区”问题，对该簇结构进行优化，具体过程如下：

①设第i个簇内节点集合为Wi={wi1,wi2,…,wimi}，簇内距离最远的两个节点为wi1(xi1,yi1)、wi2(xi2,yi2)，簇质心为centeri(xi,yi)；

②根据式（16）、（17）分别计算wavg1和wavg2，分别以wavg1(xavg1,yavg1)，wavg2(xavg2,yavg2)作为新的聚类中心，将节点分配到距离新聚类中心最近的簇中：

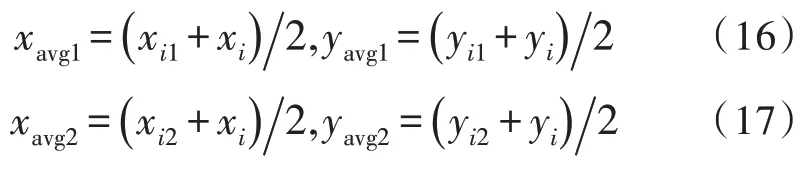
分配完成后，监测区域内的节点最终划分成了k+z个簇，z为优化后所增加簇的个数。

3.2 簇首选举

KEAC 协议在簇首选举时没有考虑节点的能量和位置，部分簇首在数据传输时能量消耗较大，导致簇首节点过早死亡，使得整个网络能量消耗不均衡，因此文中提出的算法将综合考虑节点剩余能量、节点与簇质心的距离和节点密度3 个因素，并采用改进的灰狼优化算法选举簇首，使簇首选择更加合理，从而均衡网络能耗。每个簇内节点的坐标值为改进灰狼优化算法中灰狼个体的初始值，具体过程如下：

步骤1：初始化灰狼种群，t为当前迭代次数，mi为种群大小，即每个簇中的节点数量，每个簇内的节点为灰狼个体，初始化a、A和C；初始化Xα、Xβ和Xδ的值。

步骤2：根据适应度函数计算每只灰狼个体所对应的适应度函数值。适应度函数设置如式（18）所示：

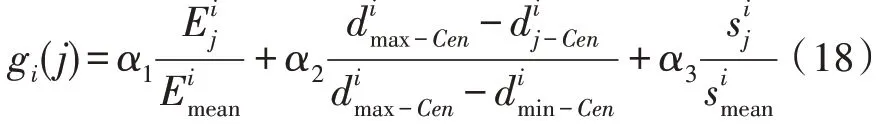
步骤3：比较灰狼个体的适应度函数值，将适应度函数值从大到小排列，排在第一位为最优解Xα，排在第二位为优解Xβ，排在第三位为次优解Xδ。

步骤4：搜索位置更新，根据式（5）～（9）更新当前灰狼个体位置。

步骤5：计算灰狼个体的适应度函数值，更新α、β、δ灰狼个体的位置，令t=t+1。

步骤6：若t>tmax，tmax为最大迭代次数，停止搜索，否则转到步骤2。

步骤7：输出最优解，最优解所对应灰狼个体的节点就是通过选举而得到的簇首。

3.3 数据传输

数据传输阶段分为簇内传输和簇间传输两个部分。簇内的每个普通节点利用单跳传输方式向簇首发送自己采集到的数据，然后簇首将节点发送过来的数据进行融合，在簇间数据传输时，将通信半径范围里与汇聚节点距离最小的节点作为下一跳节点，若簇首到下一跳节点的距离大于簇首到汇聚节点的距离，那么簇首将数据直接发送给汇聚节点，以避免产生多余的能量消耗，从而均衡网络负载，延长网络的生存周期。

4 实验设置与结果分析

为了验证文中提出的基于k-means 分簇和灰狼优化的无线传感网络路由算法的性能，将其与经典的LEACH 协议和KEAC 协议进行对比。文中采用Matlab2016a 作为仿真工具，参数设置如表1 所示，λ1=0.7，λ2=0.3，φ=0.8。

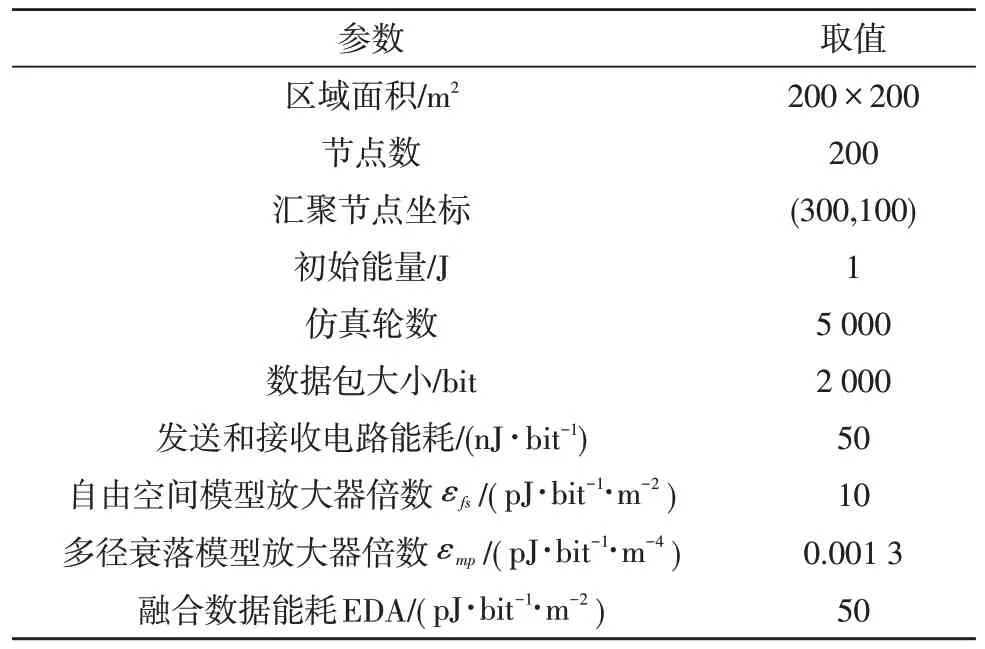
表1 参数设置

1）聚类图比较

图1 是采用k-means 算法形成的分布图，从图中可以看出簇分布不均匀，簇内节点数量分布不合理，造成有些节点能量消耗过大，网络负载不均衡。

图1 k-means算法的聚类

图2 是采用文中算法形成的分布图，从图中可以看出经过优化后的簇分布均匀，靠近汇聚节点的簇较小，有效地解决了节点能量消耗过快的问题。从而延长了网络的生存周期。

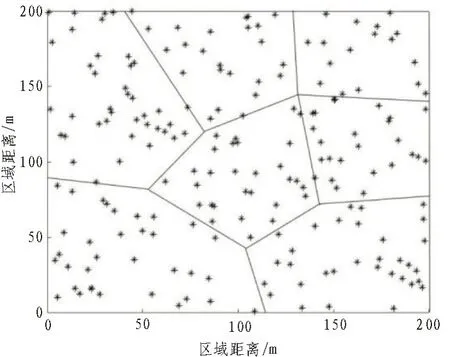
图2 改进后的聚类

2）网络死亡节点个数比较

图3 是网络死亡节点个数与轮次之间的关系，从图中可以看出，文中提出的算法在200 轮时出现了第一个死亡节点，而LEACH 算法和KEAC 算法分别在25 轮和50 轮时出现了第一个死亡节点，文中算法网络生存周期分别比LEACH 算法和KEAC 算法提高了87.5%和75%，可以得出文中算法有效延长了网络的生存时间；当LEACH 算法和KEAC 算法分别运行到2 000 轮和3 500 轮左右时，所有节点全部死亡，而文中提出的算法在3 500 轮时大概还有25 个存活节点，可以看出使用改进灰狼优化算法使簇首选择更合理，均衡了节点的能耗，显著提高了网络的生存周期。

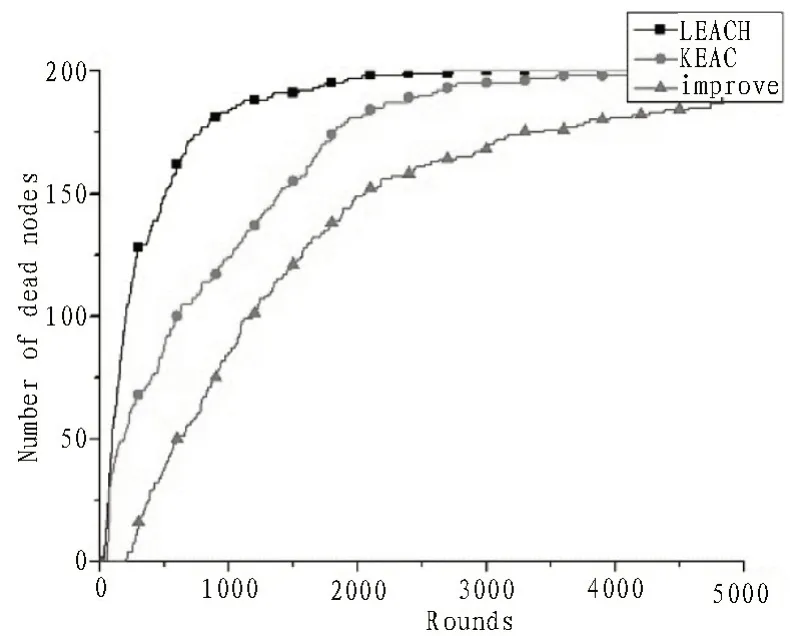
图3 网络死亡节点数与轮次关系

3）网络剩余能量比较

图4 是网络能量随时间变化的关系，在初始能量相同的情况下，LEACH 算法能量消耗显然更快，在2 000 轮时网络总能量就已耗尽，KEAC 算法在接近3 500 轮时网络的总能量耗尽，而文中提出算法的网络能耗速度均小于LEACH 算法和KEAC 算法，能量耗尽的时间较长。综上分析可知，文中提出的算法的生命周期与LEACH 算法和KEAC 算法相比有明显提高，可以看出改进后的算法能有效均衡网络的能耗[17-18]。

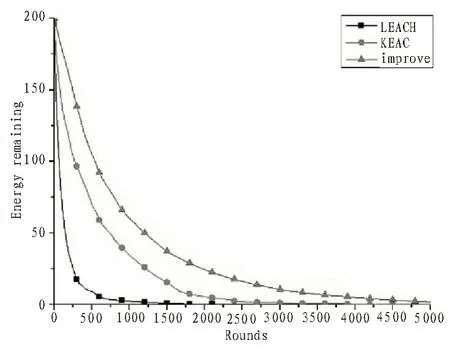
图4 网络剩余能量与轮次关系

5 结束语

文中针对无线传感器网络中簇分布不均匀、簇首选择不合理的问题，提出了基于k-means 分簇和灰狼优化的无线传感网络路由算法。该算法结合节点位置与节点密度两个方面对k-means 算法形成的簇结构进行优化，在优化后的簇中采用改进灰狼优化算法来选择簇首，在数据传输时，采用单跳和多跳相结合的方式将数据传输给汇聚节点。实验结果表明，与LEACH 和KEAC 两种协议比较，文中提出的算法解决了“热区”问题和簇首选择不合理造成的节点能量消耗不均衡的问题，有效地增加了网络的生存周期，降低了能量消耗的同时均衡了网络的能耗。