基于整数规划模型对连铸切割问题的优化

宁楠

摘要：目前，能源供應紧张成为世界各国共同关注的问题。为加快调整能源结构，优化钢坯切割过程，减少资源浪费。当待切割钢坯总长度相对固定，影响切割的主要因素为用户目标范围内的不同切割长度的根数。将切割损失最小设为目标函数，将切割后所有钢坯的长度设为决策变量，将不同切割长度的钢坯段的根数、切割后各段钢坯的和、用户目标钢坯的根数、用户目标值钢坯的根数最多作为约束条件，在整数规划基础上，建立无异常切割优化模型，得到切割余量最小且满足客户目标要求的切割方案。

关键词：连铸切割;优化模型;MATLAB

一、问题分析

连铸生产流程包括：钢水从中间包流入结晶器，按照一定速度从结晶器拉出，进入二冷段阶段，形成钢坯。按照客户要求对钢坯进行切割。在连铸停浇时，会产生尾坯，尾坯的切割也是连铸切割的组成部分。按照相关切割流程，切割机对钢坯进行切割。在切割方案中，要优先考虑切割损失尽量小，其次考虑用户目标，在切割损失相同的情况下，切割出的钢坯要尽量满足用户的目标值。

为达到切割余量最小以及客户目标要求，建立无异常切割优化模型。存在尾坯的前提为二冷段内现有的待切割钢坯，且尾坯长度虽不同，但在尾胚长度确定时待切割钢坯总长度相对固定。优先考虑切割损失最小，其次考虑用户目标需求，影响该目标的主要因素为用户目标范围内的不同切割长度的根数。通过分析，在整数规划[2]基础上，建立无异常切割优化模型，得到满足目标的最优切割方案。

二、模型建立

2.1模型假设与符号说明

1.假设在此期间装置运行不会产生故障。

2.假设不考虑冷却速度不均因素对该问题的影响[1]。

3.假设结晶器出现异常的时刻准确无误。

2.2模型需求及数据

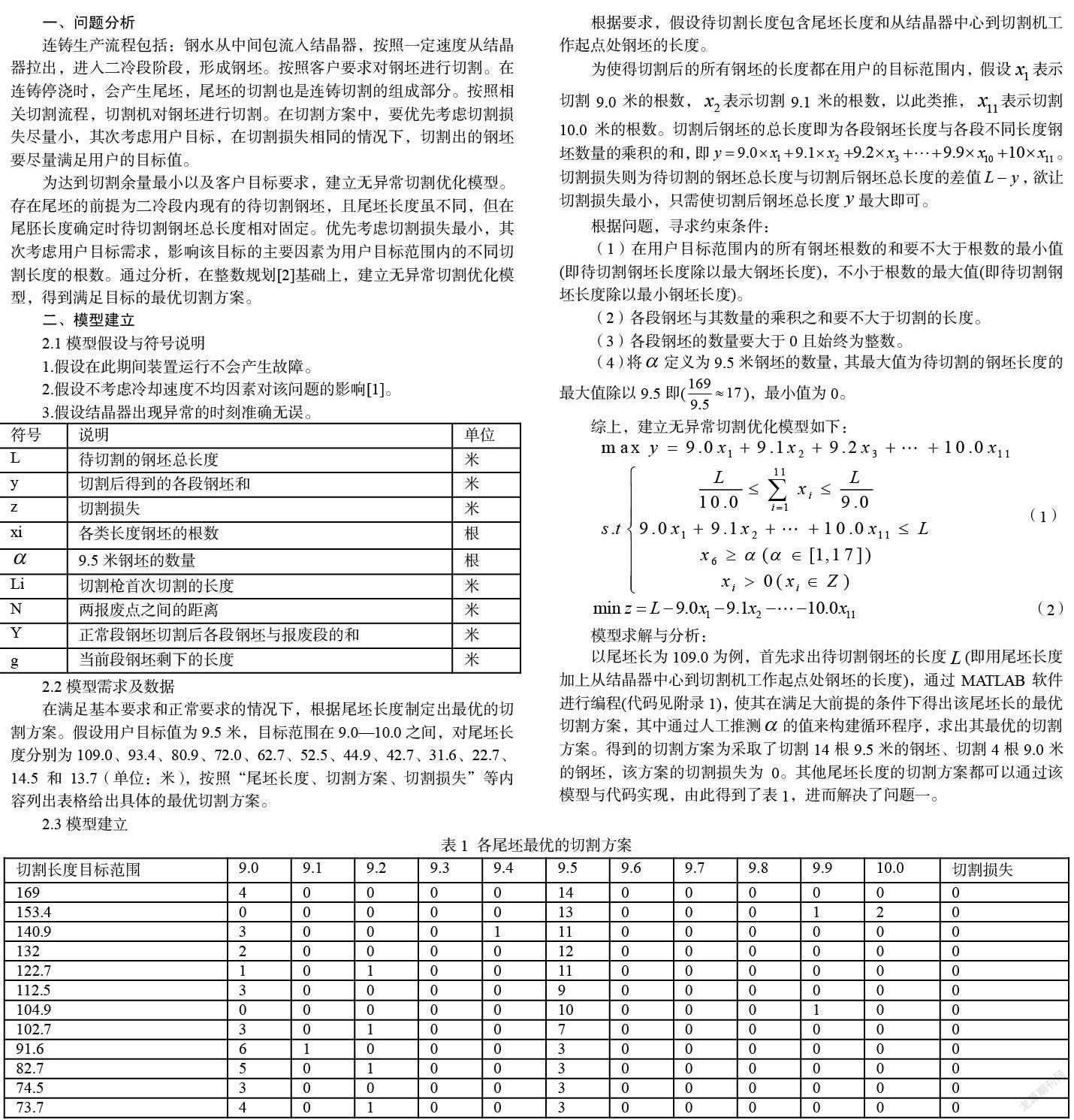
在满足基本要求和正常要求的情况下，根据尾坯长度制定出最优的切割方案。假设用户目标值为9.5米，目标范围在9.0—10.0之间，对尾坯长度分别为109.0、93.4、80.9、72.0、62.7、52.5、44.9、42.7、31.6、22.7、14.5和 13.7（单位：米），按照“尾坯长度、切割方案、切割损失”等内容列出表格给出具体的最优切割方案。

2.3模型建立

根据要求，假设待切割长度包含尾坯长度和从结晶器中心到切割机工作起点处钢坯的长度。

为使得切割后的所有钢坯的长度都在用户的目标范围内，假设 表示切割9.0米的根数， 表示切割9.1米的根数，以此类推， 表示切割10.0米的根数。切割后钢坯的总长度即为各段钢坯长度与各段不同长度钢坯数量的乘积的和，即  。切割损失则为待切割的钢坯总长度与切割后钢坯总长度的差值 ，欲让切割损失最小，只需使切割后钢坯总长度 最大即可。

根据问题，寻求约束条件：

（1）在用户目标范围内的所有钢坯根数的和要不大于根数的最小值（即待切割钢坯长度除以最大钢坯长度），不小于根数的最大值（即待切割钢坯长度除以最小钢坯长度）。

（2）各段钢坯与其数量的乘积之和要不大于切割的长度。

（3）各段钢坯的数量要大于0且始终为整数。

（4）将 定义为9.5米钢坯的数量，其最大值为待切割的钢坯长度的最大值除以9.5即（ ），最小值为0。

综上，建立无异常切割优化模型如下：

三、总结

通过对相应问题进行分析，为达到切割剩余最小的目标，结合工艺参数、基本需求及正常需求模型通过MATLAB对最优方案进行计算，能够建立无异常段切割优化模型及结晶异常切割优化模型，较好的给出了相应条件下钢坯的切割方案，实现了假设条件下的切割剩余最小。模型建立方面，本问题的优化本质上为一个动态实时优化问题，但在求解过程中仍存在人工介入的情况，因此，如何建立一个实时动态切割规划模型是一个重要研究方向。

四、参考文献

[1]张金红，贾俊礼，张淑艳.考虑冷却速度不均因素的冶金连铸二冷配水控制[J].科技通报，2014（11）：63-65+93.

[2]司守奎，孙玺菁.数学建模算法与应用[M].第11页.国防工业出版社，2011.