浅析基于蚁群算法的机器人路径规划

王轶毅 吕行军

摘要：现有大量的针对机器人路径规划的算法，但蚁群算法具有其独特优势。为了探究蚁群算法在机器人路径规划上的应用，对蚁群算法进行了简单研究，总结出其基本原理与蚂蚁选择路径的过程，之后通过设置变量、简列公式，计算出信息素浓度与路径长短的关系，并设计出其算法流程。又对路径规划问题进行了简单分析，发现蚁群算法的应用可以使机器人找到一条到达目的地最短路径，最后通过Matlab仿真确定信息素浓度与路径长短的关系，提高了分析的准确性，使其更有说服力。

关键词：蚁群算法;路径规划;最短路径;信息素浓度

0引言

机器人作为高科技时代的产物，对其路径规划能力的研究是极其重要的一方面。根据已知的环境信息和未知的环境信息，路径规划分为已知环境信息的全局规划和未知环境信息的局部规划两部分。另外，对于机器人路径规划有很多的算法。全局规划方面，如遗传算法[1]、快速随机搜索树算法、人工蜂群算法等等;对于局部规划，有人工势场法[2]、模糊算法、A*算法[3]等等。

本文要讲的蚁群算法具有较强的通用性和鲁棒性，并且适合在图上探索路径问题。蚁群算法通过对蚂蚁寻找食物的抽象化来研究信息素的挥发等因素对路径规划的影响。以此来使用蚁群算法对机器人的路径规划进行进一步探究。

1简述蚁群算法

1.1基本原理

蚂蚁在觅食时，会在经过的路径上释放一种名为信息素的物质，蚂蚁之间通过信息素传递消息，当一条路径上信息素浓度较大时，说明此路径上的蚂蚁个数较多，其它的蚂蚁也就会有更大概率选择这条路径[4]。另外，信息素会随着时间的推移而挥发。刚开始有一部分蚂蚁经过某路径，之后少数蚂蚁经过此路径，最后没有蚂蚁经过此路径，另一条被多数蚂蚁选择的路径的信息素浓度比此路径的信息素浓度高，经过一段时间，所有的蚂蚁都会选择信息素浓度较高的路径，最终形成一条最优路径。

此过程进行以下抽象：蚂蚁的巢穴视为起点，食物视为终点，信息素的浓度越大说明这条路径越短，可以将信息素浓度的大小作为蚂蚁选择路径的依据。蚂蚁在寻找食物时总是会大概率选择信息素浓度较大的一条路径，类似于最短路径的问题。

1.2工作过程

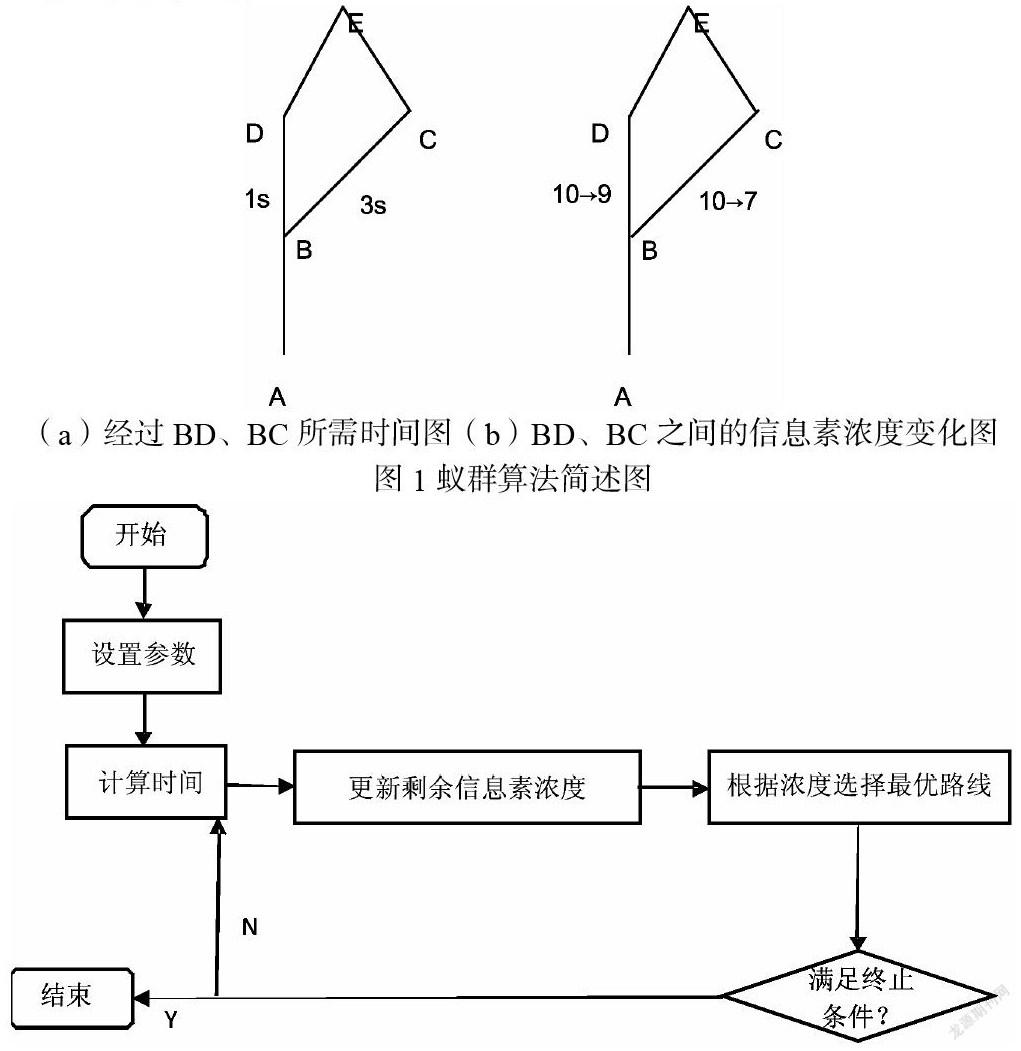
如图1，A为蚂蚁巢穴，E为食物点，可供选择的路径为ABCE或ABDE，假设DE=DC，BC>BD，每只蚂蚁释放的信息素浓度为1，信息素每过1s挥发1，第一次外出觅食的蚂蚁为20只，即AB的初始信息素浓度为20，令20只蚂蚁分为两组，每组10只，分别经过BD和BC，假设BD长度为0.05m，BC长度为0.15m，设蚂蚁行走速率为0.05m/s。由于DE=BC，所以只需在意BD段与BC段之间的差异。

使用（1）求出蚂蚁经过BD、BC的时间，如图1a。由于信息素每过一段时间会挥发，使用（2）求出蚂蚁到达D点和C点后BD和BC的信息素浓度，如图1b。BD浓度大于BC浓度，蚂蚁通过现存信息素浓度得出BD<BC，所以当仍有蚂蚁到达B点后，大概率会选择BD，随着时间的推移，选择BC的蚂蚁将会越来越少，最后蚂蚁不选择BC，而全部选择BD段，ABDE就成为了蚂蚁觅食的最短路径。

t表示时间，s表示两点间距离，v表示蚂蚁的速度，c表示信息素浓度，n表示蚂蚁个数。

1.3算法步骤

步骤1：设置参数。包括蚂蚁数量、蚂蚁行进速率、信息素挥发量、信息素初始值、两点间距离等参数的设置。

步骤2：计算时间。两点距离已知，行进速率已知，可以求出经过某一点到达另一点的时间，为计算剩余信息素浓度做准备。

步骤3：更新剩余信息素浓度。由于信息素的挥发，所以每过一段时间要计算剩余信息素浓度，方便研究蚂蚁所做出的决策。

步骤4：根据浓度选择最优路线。蚂蚁可以通过比较不同路段信息素浓度的大小判断出哪一条路径是到达下一点的最短路径，形成局部最优解。

步骤5：是否满足终止条件。是否到达食物点，当没有到达时，经过下一个不止一条路径的路口时，重复步骤2、步骤3、步骤4。当满足终止条件时，结束此算法。

2简述机器人路径规划问题

机器人路径规划问题是根据某一方面的指标（消耗最少、路径最短、所需时间最短），在规定区域内选择出一条由起点到终点最优的路径，简单来说就是在某些约束条件下得到某个问题所需最优解的问题[5]。根据周围环境的掌握程度，机器人路径规划分为全局路径规划和局部路径规划，前者是一种宏观的规划，主要为机器人在运动中提供核心运动点，保证机器人如期、按要求到达目的地，但是全局路径规划生成的不是一条连续的轨迹，而是一些离散的点，因此又称为离散域路径规划。而为了使机器人的路线更加合理，就产生了局部路径规划，它是在机器人执行任务时，随时根据自身所携带的感应器收集周围环境信息，进行实时的路径规划，在局部路径规划中，机器人由收集的周围环境的信息得出的路径很大概率上只是局部最优而不是全局最优，这便是它的局限性，局部路径规划得到的是一条连续的轨迹，所以也称其为连续域路径规划[6]。

3基于蚁群算法的机器人路径规划分析

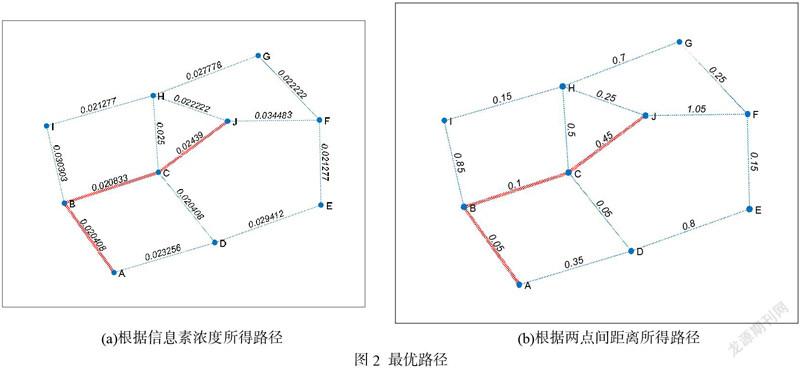
为了进一步分析蚁群算法对于路径规划的影响，使用Matlab将图1复杂化，如图2，其中A点为起点，J点为终点，其中图2a的各路径的权重采用经过一段时间后信息素浓度的倒数，路径权重越小，说明信息素浓度越大。图2b的各路径的权重为两点间的距离，不难发现，两者的解吻合。依据图2，表示机器人可以寻找到一条到达目的地最优的路径，此路径为该算法下的最短路径。

4结论

对基于蚁群算法的路径规划进行了研究，最后得出了剩余信息素的浓度越大，选择此条路径的概率就越大的结论，随着时间的推移，越来越多的蚂蚁会选择信息素浓度大的路径，最终就会形成寻找食物的最优路径。另外，当信息素浓度的挥发程度增大时，原本信息素浓度就小的路径随着时间的推移，信息素浓度会变得更小，这也使得选择这条路径的可能性减小，进而去选择信息素浓度较大的路径。

通过对蚁群算法的研究，发现此算法在机器人的规划路径中具有重大意义，可以使机器人找到一条到达目的地最短的路径。

参考文献

[1]石铁峰，改进遗传算法在移动机器人路径规划中的应用.计算机仿真，2011.28（04）：p.193-195+303.

[2]刘建华，et al.，基于势场蚁群算法的移动机器人全局路径规划方法.农业机械学报，2015.46（09）：p.18-27.

[3]沈显庆，et al.，改进A～*算法的移动机器人的路径规划.黑龙江科技大学学报，2021.31（04）：p.494-499.

[4]史恩秀，et al.，基于蟻群算法的移动机器人全局路径规划方法研究.农业机械学报，2014.45（06）：p.53-57.

[5]霍凤财，et al.，移动机器人路径规划算法综述.吉林大学学报（信息科学版），2018.36（06）：p.639-647.

[6]宋晓茹，et al.，移动机器人路径规划综述.计算机测量与控制，2019. 27（04）：p.1-5+17.