数据融合关键技术在靶场实验系统中的应用

付伟 张常玲 姜春茂 王波

摘要：在军事领域，数据融合是指根据各种信息資源，检测、关联、估计、信息、数据的多层次、多接口的信息处理，以获得准确的状态和属性，实现完整、实时的态势核威胁评估。

关键词：数据融合;滤波器;靶场实验

随着现代军工技术的发展，其先进性及复杂性对水中兵器靶场的实验技术和环境提出了越来越高的要求，以往独立运行的简单实验系统已不能满足要求，使实验系统的设计、研制、生产越来越依赖先进的实验方法。当前，我国的靶场试验体系已逐步从单科性能和指标考核发展到综合性立体化、多科目测试。靶场实验系统包含多层次、多方面数据，按信息融合思想对这些信息进行聚合，将对测量的可靠性及完整性产生积极影响，也是整个实验系统的关键。并且还能为靶场试验数据的下一步数据挖掘提供丰富信息源，从而实现设计和试验的迭代发展。

一、数据融合概述

数据融合也称信息融合，是利用计算机技术对按时序获得的若干传感器观测信息在一定条件准则下予以自动分析、综合完成任务所需决策和评估而进行的信息处理过程。由于数据融合技术在现代军事中起着重要作用，因而被广泛运用于军事领域。

二、时空对准技术

分布在不同平台上的不同类型传感器具有不同位置、不同观测坐标系、不同采样频率。因此，即使观测相同目标，每个传感器获得的目标观测数据也会不同。因此，先要将来自不同平台的多传感器数据在空间与时间上整合，将来自不同传感器获得的目标观测数据转换到统一坐标系中，统一量测单位。

空间对准是选择一个基准坐标系，将来自不同平台的多传感器数据统一到该坐标系中。位于不同平台上的多传感器系统通常采用大地坐标系，用于数据融合的坐标系则采用地理坐标系。转换过程为：

1、地理参考系中，选择一个点作为坐标原点，建立直角坐标系，作为数据融合的基准坐标系。

2、各平台目标的采样数据通过旋转和平移从大地坐标系转换到参心空间直角坐标系，并在参心空间直角坐标系中对齐。

3、各平台目标采样数据从参心空间直角坐标系转换到选定的基准地理坐标系中。

多传感器工作时，时间上不同步，其原因为：每个传感器启动时间不同;不同脉冲重复周期及扫描周期导致不同采样率;扫描时，观测数据存在时间差。这样，这些观测数据必须在融合前同步，或称为时间对准，即统一“时基”。通常，使用一个传感器的时间作为公共处理时间，将其他传感器时间统一到该传感器时间上。当然，卡尔曼滤波器的预测方程与误差协方差也可直接同步到融合中心时间上。另外，还可通过插值将每个传感器测量数据与统一时间轴对齐。

三、快速改进的JPDA算法

JPDA算法是公认的经典数据关联算法，但随着有效回波数与目标数行的增加，可能的联合事件总数急剧增加。因此，在密集多回波环境下跟踪机动多目标时会出现复合爆炸现象，计算量难以承受，所以寻求一种有效快速或简化算法在实际应用中具有重要意义。

基于多目标数据关联算法思想，可设计一种宽度优先搜索算法来生成所需量测关联假设。所有关联假设都可排列成一棵生成树，树的每个节点都是一个联合事件，即关联假设。在多目标跟踪过程中，数据关联问题总有一个解，即最优分配解。由于“最近邻域法”简单且易于工程实现，因此该方法可用于在初始状态下寻找根节点。然后，采用系统化方法依次搜索，展开所有节点。搜索时，除满足联合概率数据关联的两个基本假设外，还有一个条件，即先选择统计距离最小赋值，以便在搜索时始终先获得最可能的赋值。根据时间问题的复杂度及所需跟踪精度，可控制搜索深度，从而有效控制算法复杂度。

此外，根据“最近邻”原则得到初始解，即最优分配解。在联合事件生成树中，树的每个节点都是一个可能事件（FeasibleE-vent），根节点是最佳分配（0ptimal）。第一层节点是近优分配（Near-Optimal），第二层节点是次优分配（Sub-optimal），层数越大，可能概率越小，联合概率计算中影响越小。因此，控制搜索层数能极大地提高关联概率并保持较好的关联精度。

四、推广的卡尔曼滤波（EKF）算法

卡尔曼滤波器在许多领域有着广泛的应用。在通信、雷达、自动控制等领域，卡尔曼滤波器能用来从被噪声污染信号中恢复有用信号的波形，或估计状态。然而，由于使用的动态、观测方程为线性，在许多实际应用中，传感器给出目标的斜距、方位角、高低角，数据与目标又是非线性;要么状态方程是非线性，测量方程是线性。这就是现代跟踪技术中经常使用混合坐标系的原因。扩展卡尔曼滤波器是一种使用混合坐标系进行滤波及残差计算的卡尔曼滤波器。在实际运算中，其动态、测量方程是线性的。扩展卡尔曼滤波器与标准卡尔曼滤波器的区别在于：①采用极坐标系计算残差;②跟踪计算采用直角坐标系;③输出数据为直角坐标系数据;④在两者交界处进行相应坐标变换。

五、靶场数据融合的仿真

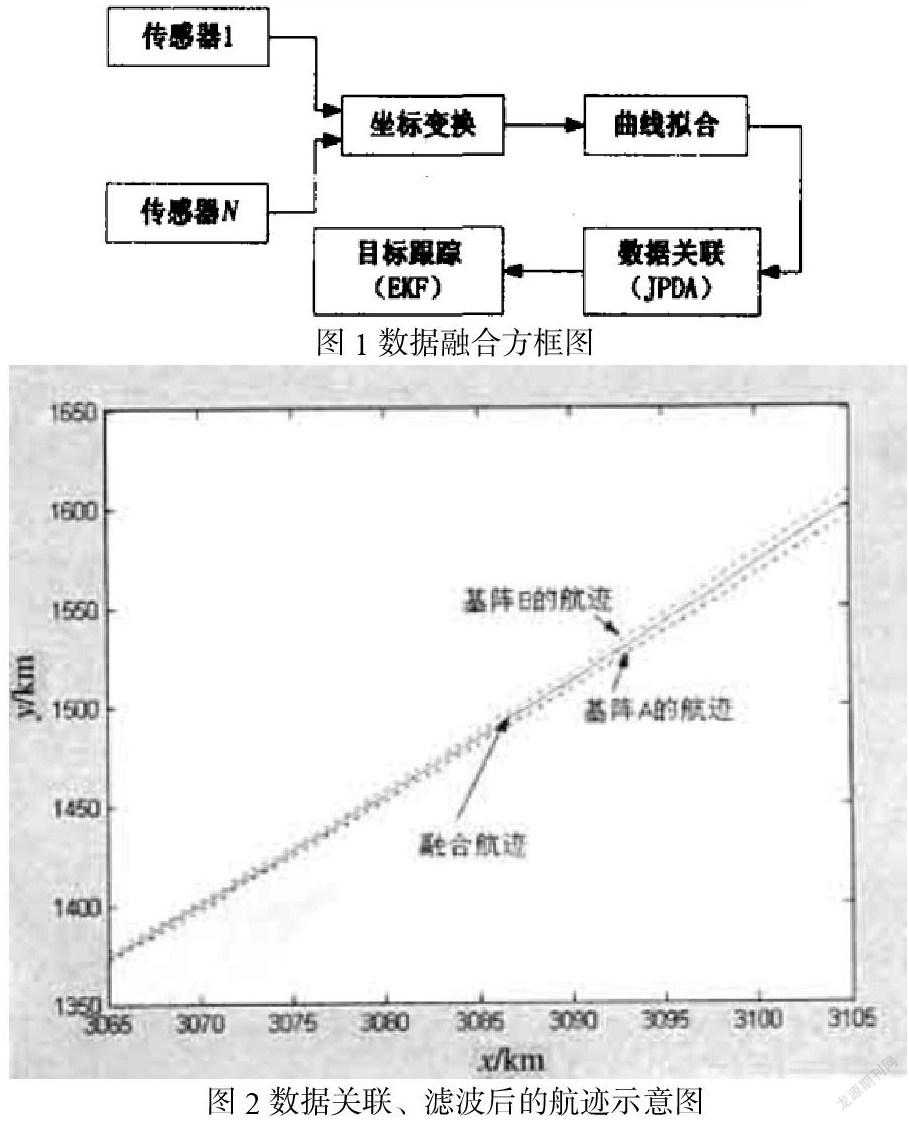
由于靶场测试环境具有以下特点：①单传感器跟踪精度低;②通常，网络环境中目标少，因此数据量小，所以可采用集中式集成。图1为鱼雷靶场测试系统的数据融合方框图。每个传感器先将其对目标的观测数据传输到数据融合中心，融合中心通过时间外推及坐标变换将观测数据转换为同一时间及公共坐标系（以融合中心为坐标原点（，然后采用最小二乘法对两个传感器观测数据进行拟合，然后使用快速JPDA算法关联数据，即确定这些数据是否由同一目标生成。最后，利用EKF算法对相关数据进行滤波，得到目标位置的估计值，从而实现对目标的精确跟踪。

本文涉及的靶场属于固定短基线跟踪靶场，即目前使用的三维跟踪靶场。可确定装有相应声脉冲发射机的航行体轨迹，并记录试验过程中武器系统的动态特性及环境参数，从而确定系统性能限度。

短基线跟踪靶场工作原理要求被跟踪物体周期性地发射声脉冲信号，并根据脉冲信号向传感器的传播时间确定被跟踪物体位置。短基线跟踪靶场内的四个传感器配置在立方体中。

基阵确定用于表示测量值的直角坐标系。当跟踪物体发出的声脉冲到达四个传感器时，通过传播时间获得位置信息，计算机使用这4个时间3次简单计算三个空间坐标。

此外，若不考虑干扰问题，则可在靶场上连续跟踪的目标总数取决于基阵重叠区的重叠程度，这是因在重叠区内，每个基阵将为被跟踪的单个目标生成一个输入，因此计算机将单个目标视为两个目标，所以数据关联工作非常重要。另外，每个基阵坐标系计算的坐标值必须转换为公共坐标系，以便于融合处理及显示。

假设基阵A、B分别位于被跟踪物体两侧，其基阵接收频率为1500kc，计算周期为0.661s，相对精度为±1。基阵A、B分别计算被测物体的三个坐标，并将坐标转换为靶场的统一坐标系。

生成模拟数据时，假设被测物体以5km/h、60km/h的速度通过两基阵的中心线，并与两基阵保持相等距离。以V=5km/h为例，由于目标运动速度较慢，在不同时间同一方位角上会有多个不同距离的点，在获取观测数据时，需判断这些数据是否由同一目标生成，可设置距离阈值（本文中d=40m），设

其中，是k时刻的观测值;是时间k-1在内所有先前观测数据对k时刻信号数值的预测值，当d（k）≤d时认为k时刻观测值属于该目标。通过这种方式，可删除一些虚警或其他目标生成的点。

根据图1所示进行融合处理，两个基阵的观测数据用最小二乘法拟合。图2显示了使用快速JPDA算法进行关联处理及使用EKF滤波算法对关联数据进行估计跟踪后的航迹。

当目标速度较小时，融合后的航迹精度较高。这是因目标运动缓慢，基阵有较多关测点，即获得更多的目标信息。由此可知，图1所示的数据融合过程是有效的，提高了单个基阵的测量精度。

参考文献

[1]杨万海.多传感器数据融合及其应用[M].西安：西安电子科技大学出版社，2015.

[2]彭应宁.多传感器信息融合及应用[M].成都：电子科技大学出版社，2015.

[3]任晓庆.数据融合关键技术在靶场实验系统中的应用[J].计算机测量与控制，2015（10）.