基于GIS和logistic模型的地震滑坡致死人数快速评估方法

白仙富 聂高众 叶燎原 戴雨芡 余庆坤

1)云南师范大学地理学部， 昆明 650500 2)云南省地震局， 昆明 650224 3)中国地震局地质研究所， 北京 100029

0 引言

在高山峡谷地区， 地震通常会引发严重的山体滑坡(Pain， 1972)， 且滑坡体将对下方的居民点造成冲击， 使其成为地震导致人员伤亡的主要因素之一。美国阿拉斯加大地震导致130人死亡， 其中48人死于地震滑坡(Keeper， 1984)。1969—1993年20多a间， 日本M≥6.9地震造成的死亡人数中一半以上源于地震滑坡(Kobayashi， 1994)。1970年的秘鲁钦博特7.6级地震引发了迄今为止国外最大的地震滑坡灾难性事件， 此次地震滑坡至少造成2万人死亡(Plafker， 1971)。地震滑坡在中国也十分常见， 特别是西部山区， 在该区域发生的几乎所有的强烈地震都会引发大量滑坡， 并造成不同程度的人员伤亡， 简要统计结果如表1 所示。

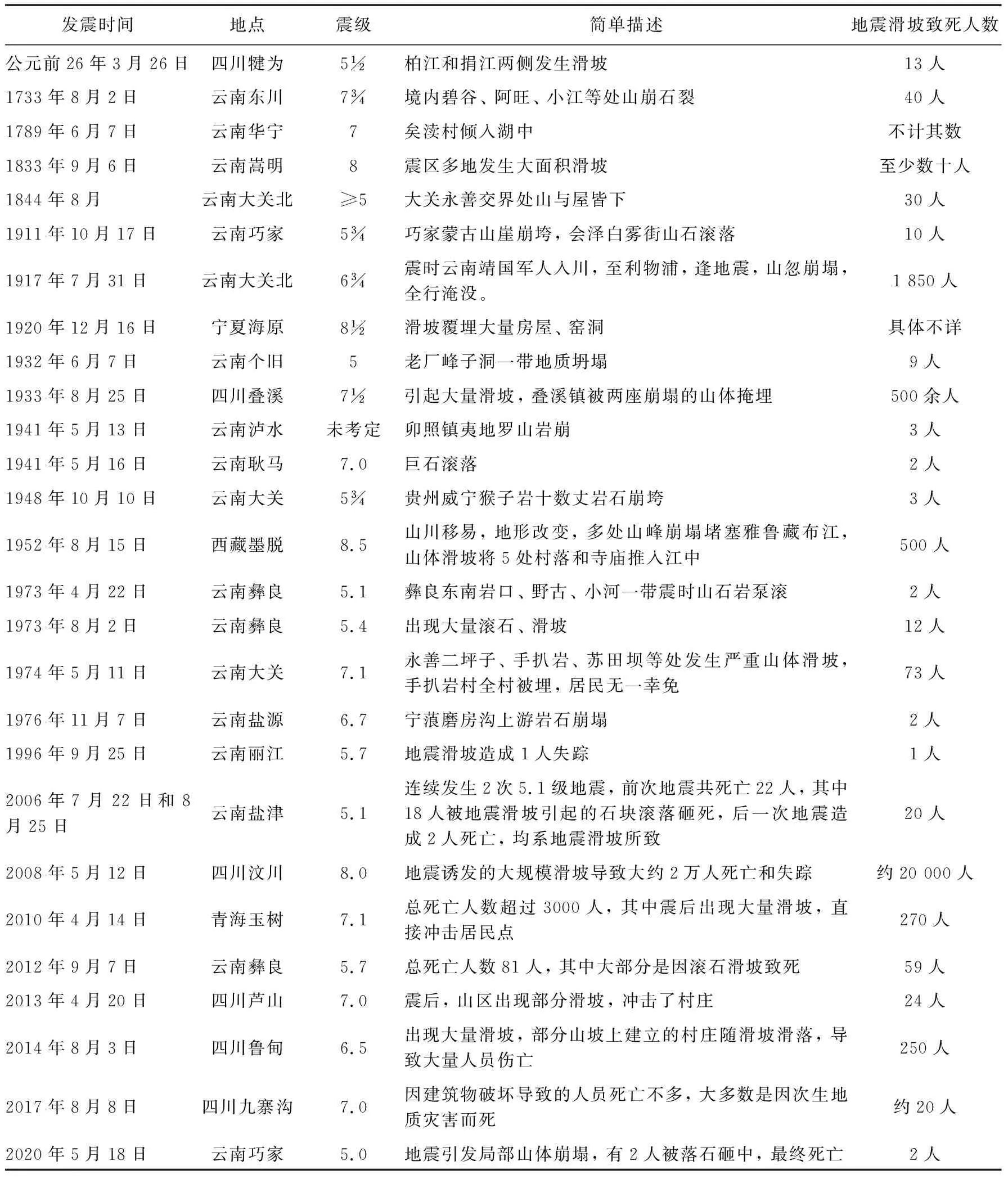
表1 中国部分地震滑坡灾害导致的人员死亡列表Table1 Death toll from the historical earthquake-induced landslides disasters in China

从历史统计来看， 在中国西部山区地震导致的人员伤亡中， 地震滑坡致死人数可能占总死亡人数的25%～30%。在个别震例中， 地震滑坡导致的死亡人员数甚至超过建筑物破坏导致的死亡人员数(高庆华等， 2011)； 而一些震级较小的死亡人数为1至数人的地震事件， 人员死亡可能仅由地震滑坡所致， 说明地震滑坡已经成为中国西部山区人民面临的主要风险隐患之一。结合《中国地震动参数区划图(GB18306-2015)》推测， 未来中国西部地区仍面临着较高的地震滑坡人员伤亡风险。要提高中国西部山区地震人员伤亡快速评估的准确性， 除了继续发展和完善建筑物破坏导致人员伤亡的评估技术之外， 必须尽快建立和发展针对地震地质灾害导致人员伤亡的评估方法(白仙富等， 2014)。科学评估地震滑坡灾害可能造成的人员伤亡， 是提高地震人员伤亡评估的准确性进而完善地震灾害损失评估体系的关键科学问题之一， 同时也是一直困扰地震灾害风险评估和震后高精准快速评估的技术难题之一。

发展地震滑坡灾害导致人员伤亡的评估方法主要包括2个阶段： 第1阶段是探讨地震发生后评估地震滑坡灾害危险性的方法， 即回答“什么样的地震会导致滑坡灾害”以及“可能在什么地点发生滑坡灾害”的问题。众多研究者对地震滑坡灾害的危险性评估进行了多年探索和研究， 发展出多种方法， 已经从定性评估逐渐走向半定量、 定量化评估(陈晓利， 2011； Yuanetal.， 2013； 刘甲美等， 2016； 许冲等， 2019)。第2阶段是研究地震后出现的这些滑坡灾害是否会导致人员伤亡， 以及可能导致多少人员伤亡， 即地震滑坡灾害的危害性评估问题。历史上在进行地震人员死亡统计时， 通常只关注建筑物造成的人员死亡情况； 偶有针对地震滑坡致死的考察， 但也几乎不记载滑坡遇难者的具体位置等信息， 使得我们难以进行以地震参数、 滑坡位置、 居民点位置与地震滑坡致死人数的关系为对象的研究。也正是因为历史记录的不完善， 至今仍很少见到关于地震滑坡灾害危害性方面的正式研究文献， 导致长期以来在地震损失快速评估或重点危险区损失预评估等工作中， 对地震滑坡致死人数的预测更多还只能停留在专家经验估计的层面上， 无法保证其准确性。对该问题的关注和研究正是本文的主要目标。

1 研究思路与方法

1.1 基本思路

图 1 全区域和分区域人口信息示意图Fig. 1 A sketchmap showing the demographic information in the whole region and the sub-regions.

根据上述推理认识， 本文提出一种基于GIS和logistic模型的地震滑坡致死人数快速评估方法。该方法的基本思路(图 2)是： 各公里网格单元的地震滑坡致死率与其内部的滑坡危险性等级属性和数量相关， 并据此建立公里网格单元的地震滑坡致死率模型； 评估区域内的地震滑坡致死人数等于区域范围内所有公里网格单元的地震滑坡致死人数之和。

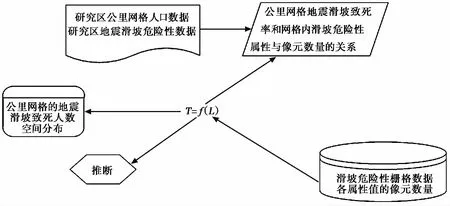
图 2 地震滑坡致死人数评估的基本思路Fig. 2 Basic ideas of the evaluation of the death toll from earthquake-induced landslides.

本研究所提出的地震滑坡致死人数评估方法的关键点在于构建针对公里网格单元尺度的地震滑坡致死率模型。由于难以准确评估某个确定地点内是否发生滑坡， 因此， 选取地震滑坡危险性作为网格单元的地震滑坡致死率影响因子。地震滑坡危险性作为影响因子， 采用公里网格单元内不同滑坡危险性属性像元数量的线性组合表示， 通过逻辑回归求解线性组合中的未知参数建立基于公里网格单元的地震滑坡致死率模型。在此基础上引入公里网格单元内的人口数量， 最终建立基于公里网格单元的地震滑坡致死数量评估模型。本研究中， 用GIS统计各公里网格单元内不同滑坡危险性属性的像元数量并计算网格单元的地震滑坡致死人数及死亡率等， 通过获取这些参数提出公里网格的地震滑坡致死率与其内部各属性值的滑坡危险性像元数量之间的联系：

Mi=f(Xil)

(1)

式中，Mi表示第i个公里网格单元的地震滑坡致死率，f为推断的影响因素与Mi的关系，Xil表示第i个公里网格单元内各属性值的滑坡危险性像元数量。

按照上述思路， 针对公里网格地域单元的地震滑坡致死人数快速评估方法一般分为3个步骤(图 3)： 1)在GIS中将研究区划分为1km×1km的网格单元， 把网格内的人口数量信息赋值给网格作为其人口属性值； 2)计算网格单元的地震滑坡致死率。通过GIS的空间分析功能从预测数据集中提取研究区的地震滑坡危险性数据， 并统计网格单元内各滑坡危险性属性值的像元数量作为网格单元的滑坡危险性属性， 根据滑坡危险性属性基于统计的logistic模型计算网格单元的地震滑坡致死率； 3)评估公里网格单元地震滑坡致死人数分布和整个研究区地震滑坡致死人数。

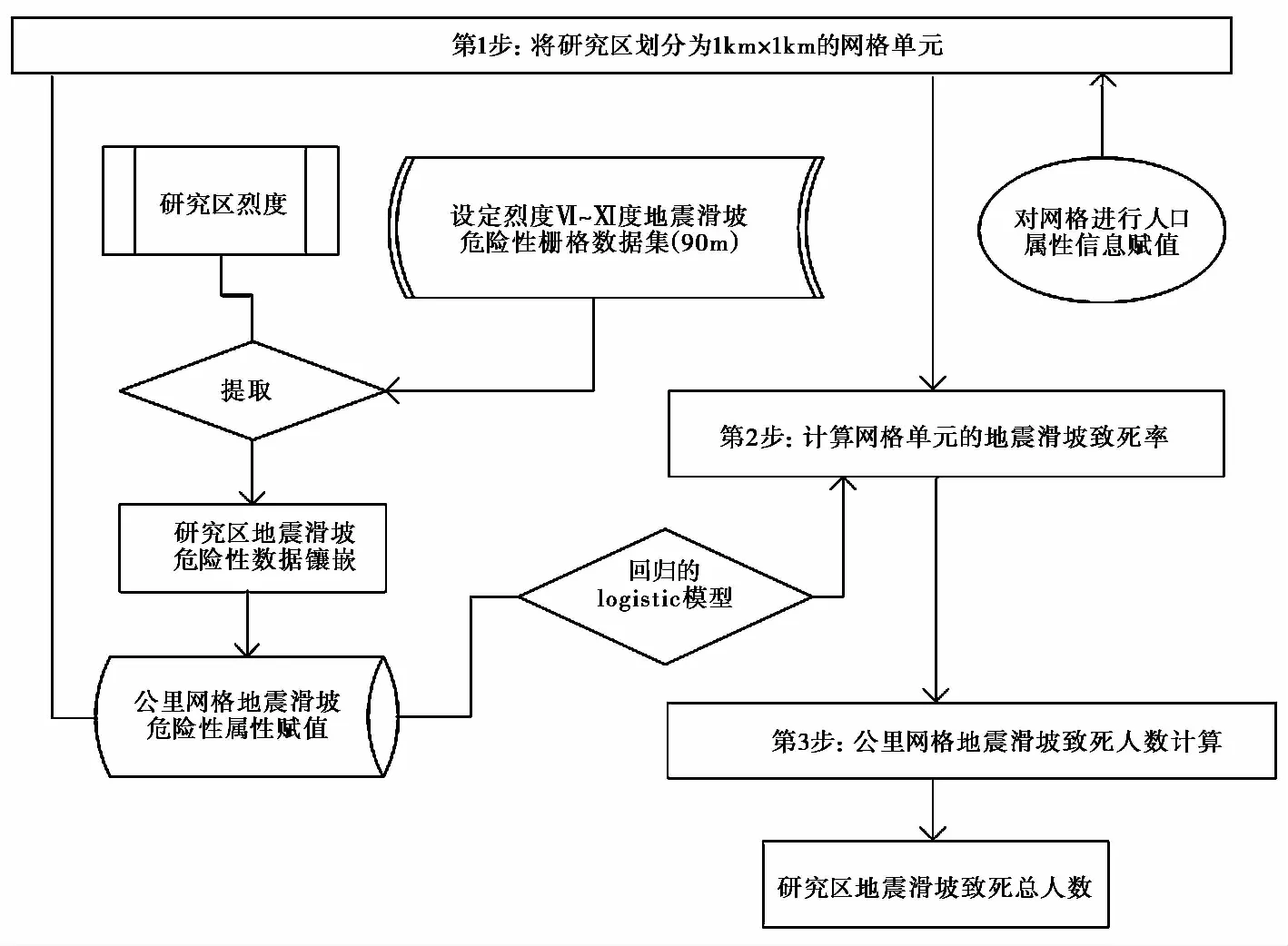
图 3 地震滑坡致死人数的快速评估流程Fig. 3 Procedure of the rapid assessment of death toll from earthquake-induced landslides.

1.2 研究方法

1.2.1 公里网格人口属性赋值

本研究使用中国地震局地质研究所和中国科学院地理科学与资源研究所合作开发的中国大陆公里网格人口数据集， 该数据集的适用性已经得到验证(陈振拓等， 2012； 丁文秀等， 2014； 安基文等， 2015)， 且数据具有良好的更新机制。

1.2.2 建立地震滑坡危险性数据

本文利用“十一五”国家科技支撑课题“重大地震灾害及其灾害链综合风险评估技术”产出的地震滑坡危险性评估模块绘制地震灾区滑坡危险性分布预测图。该模块可给出不同烈度条件下的地震滑坡危险性空间分布状况， 其产出的数据集为90m×90m栅格数据， 根据地震滑坡概率值从小到大将滑坡危险性划分为5个等级， 危险性等级从低到高的属性值依次为1、 2、 3、 4、 5。属性值从1到5， 表示地震滑坡危险性等级从极低到极高(图 4)， 属性值越高， 发生滑坡的可能性越大(白仙富等， 2015)。图 4 中， 每个栅格的属性值即代表该空间位置的地震滑坡危险性等级。以往的地震应急和地震灾害风险预评估中的试验性应用表明该套数据具有很好的合理性和实用性(Anetal.， 2015； 白仙富等， 2015； 高娜， 2015； 张如前， 2015； 魏连雨等， 2016； 张超， 2016； 邱丹丹等， 2017； 曹彦波等， 2018； 裴强等2018； 易树健等， 2018； 邓树荣等， 2019； 杨根云等， 2019)。本文在利用该数据集生成研究区地震滑坡危险性数据时， 使用现场调查后确定的烈度从数据集中提取对应烈度区的地震滑坡危险性等级数据， 然后通过GIS镶嵌功能建立整个研究区地震滑坡危险性空间分布数据(图 5)。

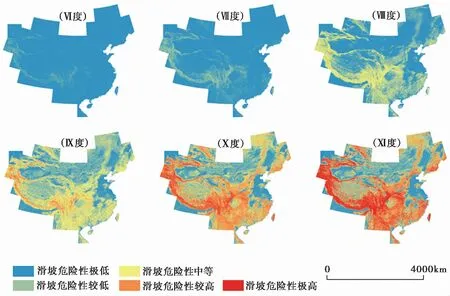
图 4 Ⅵ～Ⅺ度地震烈度设定下地震滑坡危险性等级空间分布(90m栅格数据)Fig. 4 Landslide susceptibility distribution assuming different seismic intensities， panels Ⅵ～Ⅺ show the landslide susceptibility according to intensity Ⅵ～Ⅺ(90m grid)， respectively.

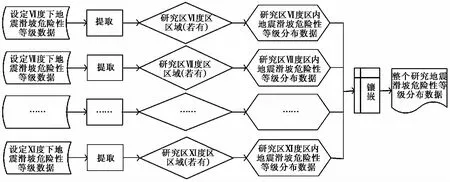
图 5 建立地震滑坡危险性数据流程图Fig. 5 A flow chart showing the susceptibility dataset of the earthquake-induced landslide.

1.2.3 公里网格地震滑坡属性赋值

建立研究区的地震滑坡危险性等级数据后， 在GIS中通过空间关联统计功能模块对每个公里网格单元内的地震滑坡危险性像元信息进行统计， 统计对象为像元中心点完全落在公里网格单元内的滑坡危险性数据。 统计各个公里网格单元内每类属性值的滑坡危险性像元数量， 并将统计结果作为属性值赋值给对应的公里网格作为其地震滑坡属性(表2)。公里网格单元属性示例表中， FID表示字段的机器自动编码， 若研究区共有N个公里网格单元， 编码从0开始到N-1结束， 共N个字段编码。P为人口字段名， 表中的PN表示第N个公里网格单元内的人口数为PN人；X1表示属性为1的地震滑坡危险性像元字段名，X2等以此类推；X1，1表示第1个公里网格单元内属性值为1的滑坡危险性像元个数为X1，1个，X1，2表示第1个公里网格单元内属性值为2的滑坡危险性像元个数为X1，2个，X1，3等以此类推。在实际的属性表中，X1，1—XN，5均为非负的整数型数值。

表2 公里网格属性示例表Table2 A sample table of kilometer-grids’ properties

1.2.4 公里网格地震滑坡致死率函数

将公里网格单元的地震滑坡致死率与其内部不同属性值的滑坡危险性像元数量之间的关系描述为函数f。 将滑坡危险性的属性看作地震滑坡致死率的影响因子， 根据影响因子的数据属性， 函数f可以有不同的选择， 例如：

Mi=f(Xi，1，Xi，2，Xi，3，Xi，4，Xi，5)

(2)

式中，Mi表示第i个公里网格单元的地震滑坡致死率，f表示推断的影响因子与Mi的关系，Xi，1～Xi，5为地震滑坡致死率影响因子，Xi，1表示第i个公里网格单元内地震滑坡危险性属性为1的像元数量，Xi，2表示第i个公里网格单元内地震滑坡危险性属性为2的像元数量， 其余以此类推。理论上， 1个公里网格单元的地震滑坡致死率最低为0， 最高为1， 随着地震滑坡危险性属性这一影响因子的变化而相应地变化， 这种范围增长率的变化和影响因子之间的关系通常可以用logistic模型进行描述， 则将式(2)表达为常用的logistic模型：

(3)

式中，Mi表示第i个公里网格单元的地震滑坡致死率， 取值范围为0～1，k表示关系式函数的系数，a0是常数项，a1、a2、a3、a4、a5表示影响因子(滑坡危险性属性)的参数，Xi，1～Xi，5分别为第i个公里网格单元内地震滑坡危险性属性值为1～5的像元数量。模型中的未知参数k、a0、a1、a2、a3、a4、a5可通过多次观察样本数据获得。求解时， 把样本数据中每条数据作为一次观察数据， 一共观察N次。假设每条样本数据都满足式(3)， 则：

(4)

式中，i表示第i次观察， 共观察N次。观察的目标就是利用数据和这些函数关系估计未知参数k、a0、a1、a2、a3、a4、a5。在统计学上， 把致死人数di看作随机变量， 且具有如下分布规律：

(5)

N次观察的似然函数为

(6)

为便于计算， 通常取对数， 因此有对数似然函数：

(7)

将式(4)代入式(7)可得：

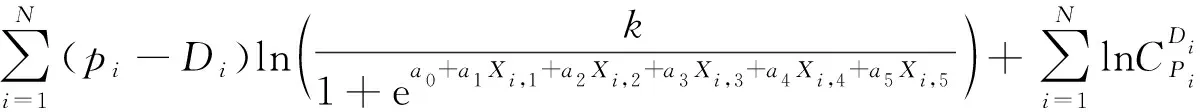
(8)

该函数中，N、Pi、Di、Xi，1、Xi，2、Xi，3、Xi，4、Xi，5是已知的， 即为我们观察到的样本数据， 故该函数为未知参数k、a0、a1、a2、a3、a4、a5的函数。未知参数k、a0、a1、a2、a3、a4、a5的最大似然估计应使得对数l(k，a0、a1、a2、a3、a4、a5)似然函数取得最大值。函数l(a0、a1、a2、a3、a4、a5)表达式的最后一项和k、a0、a1、a2、a3、a4、a5无关， 求解优化问题时可以省略， 即只需求解如下函数的最大值点：

(9)

该函数优化问题的解需采用数值模拟方法求得， 即通过样本数据进行模拟求取。

1.2.5 地震滑坡致死人数评估

整个区域的地震滑坡致死人数等于区域内各公里网格单元致死人数的总和。根据1.1节所述的基本思想， 若将区域R划分为N个1km×1km的网格单元， 总死亡人数D可以通过式(10)进行评估：

(10)

式中，D表示区域R内地震滑坡致死人数，N表示区域R内共划分为N个公里网格单元，Di表示区域内第i个公里网格单元的地震滑坡致死人数。评估时通常需要对计算得到的直接结果D进行取整处理。

2 震例案例

2.1 研究区域

本文选取2014年鲁甸MS6.5地震灾区、 2012年彝良MS5.7、MS5.6地震灾区和2008年汶川MS8.0地震灾区3个区域(图 6)为研究区， 检验所提出的基于GIS和logistic模型的地震滑坡致死人数快速评估方法。3个研究区是川滇乃至整个西南高原山地的典型区域， 对中国其他山区也有一定的代表性。这3个研究区中， 使用地震死亡人员样本数据最详实的鲁甸灾区的相关数据构建地震滑坡致死人数快速评估方法并评价其有效性。彝良和汶川研究区数据则用来对构建方法在更广研究范围内开展地震滑坡致死人数评估的外延适用性进行评价。

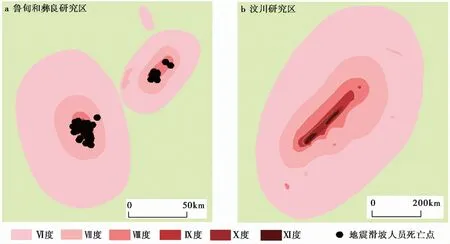
图 6 案例研究区域Fig. 6 The case study areas.

2.2 建立公里网格人口数据

在汶川研究区， 用2007年的人口数据对研究区的公里网格单元进行人口属性赋值， 对彝良研究区和鲁甸研究区使用2011年的人口数据对公里网格单元进行人口属性赋值， 得到研究区具有人口属性值的公里网格空间数据(图 7)。

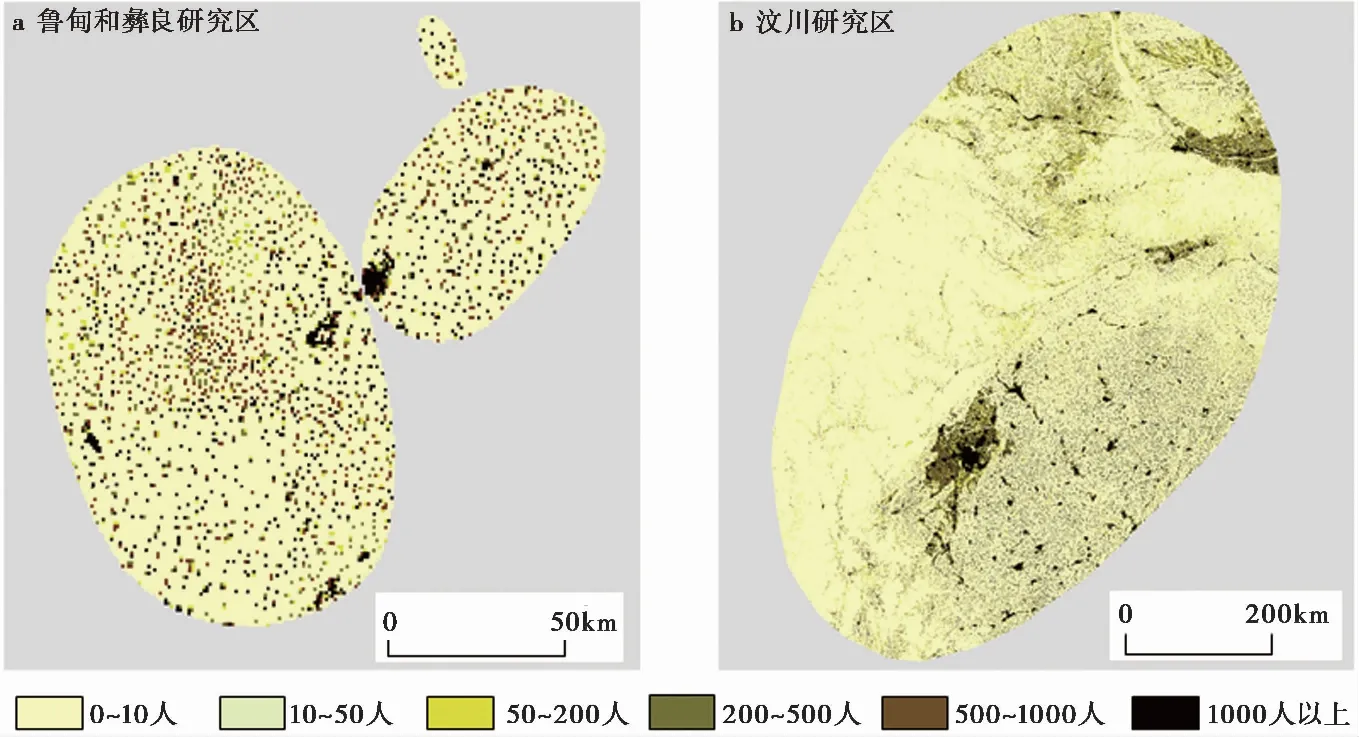
图 7 研究区公里网格人口数量的空间分布Fig. 7 The kilometer-grid population distribution in the study areas.

2.3 反演地震滑坡危险性数据

按照1.2.2节所述， 建立研究区的地震滑坡危险性空间分布数据(图 8)， 并按照1.2.3节所述方法， 对研究区内的公里网格单元进行滑坡危险性赋值， 最终建立具有人口、 滑坡属性的公里网格单元数据， 数据属性如表2 所示。

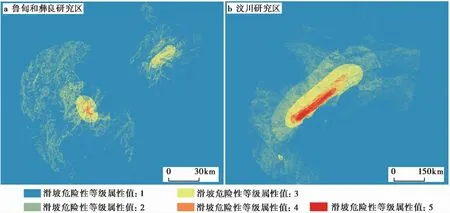
图 8 研究区地震滑坡危险性空间分布反演Fig. 8 Inversion of the distributions of the landslide susceptibility in the study areas(assessed results).

2.4 鲁甸研究区模型的建立及其评价

2.4.1 地震滑坡致死率影响因子分析

2014年8月3日鲁甸MS6.5地震滑坡直接造成134人死亡和116人失踪， 我们将失踪人员等同于死亡人员， 把250人作为该次地震滑坡致死总人数。根据地震滑坡致死和失踪人员的具体空间信息， 计算出研究区每个公里网格单元的地震滑坡致死人数和致死率。鲁甸研究区共包括10395个公里网格单元， 故有10395条地震滑坡致死率信息， 限于篇幅， 此处仅列出部分结果(表3)。列出的数据中不包括地震滑坡致死人数为0的网格单元信息， 但在整个研究区， 绝大多数网格单元内实际地震滑坡致死人数均为0， 且这些滑坡致死人数为0的网格单元中大部分为无人区。有滑坡致死的网格单元主要分布在烈度为Ⅸ度的区域。属性表中，P表示公里网格单元的人口数字段名；D表示公里网格单元的地震滑坡致死人员数量字段名；M表示公里网格单元的地震滑坡人员致死率字段名， 由各网格单元对应的D/P得到；X1～X5分别表示公里网格单元内地震滑坡危险性属性为1～5的字段名， 表中X1对应的数字是该公里网格单元内属性为1的地震滑坡危险性像元数量，X2对应的数字是属性为2的地震滑坡危险性像元数量， 以此类推。

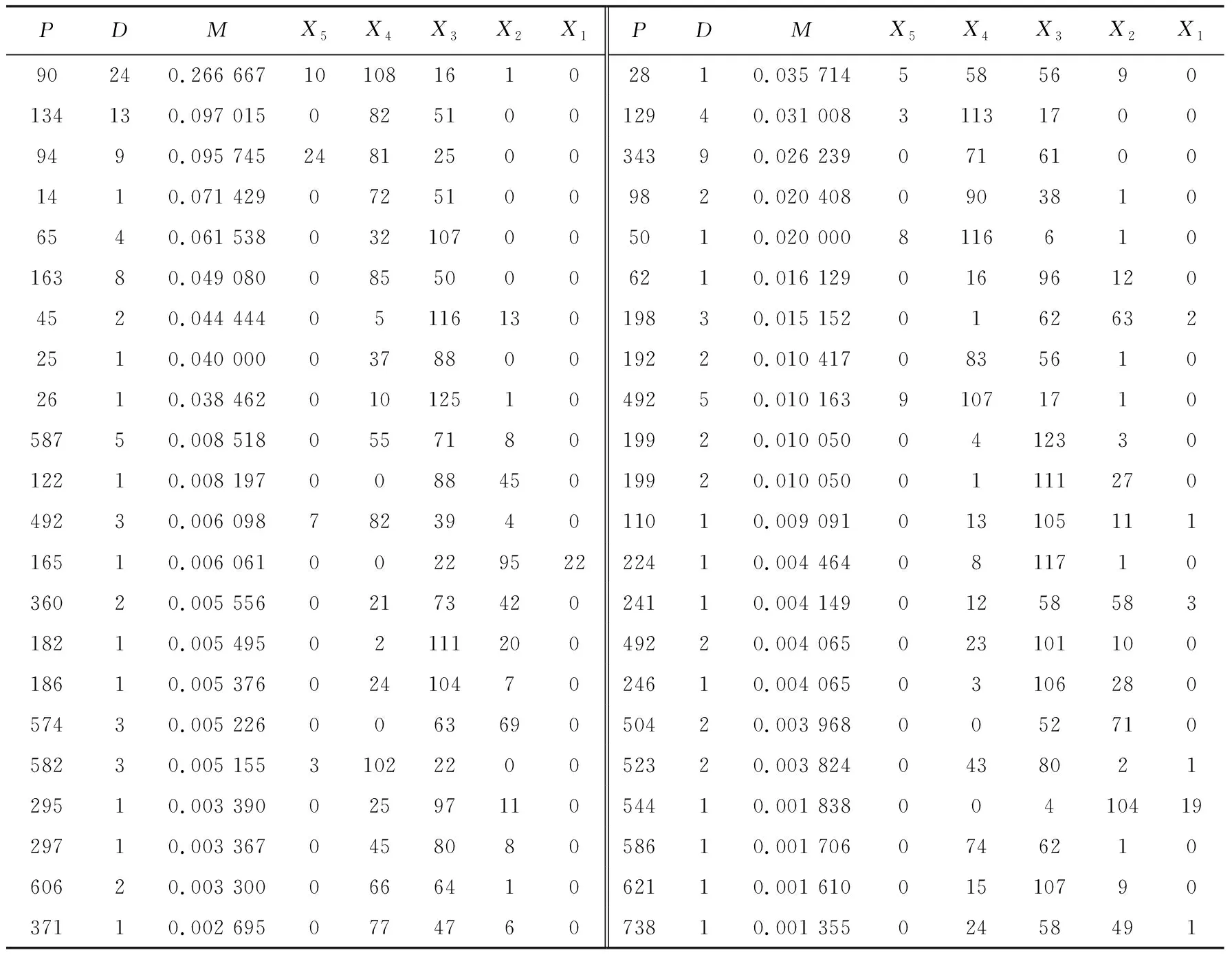
表3 鲁甸研究区公里网格单元属性表(部分)Table3 Property of the kilometer-grids in Ludian study area

为了判明公里网格单元地震滑坡致死率与网格内每类地震滑坡危险性像元数量之间有无关联， 即是否独立， 采用列联表(contingency table)对鲁甸研究区10395个公里网格单元的地震滑坡致死率与地震滑坡危险性属性的相合性进行分析与推断。我们把滑坡死亡率分为“>0”和“=0” 2类， 分别考虑不同地震滑坡危险性属性值与死亡率分类之间的相合关系。通过建立滑坡危险性属性像元数量与死亡率的列联表(表4)， 对X1～X5与M分别进行列联分析。分析方式为： 原假设H0，X1～X5与M相互独立； 备择假设H1，X1～X5与M正相合， 检验数据支持哪个命题。X5与M的列联分析检验p值为1.773×10-93， 相合系数为0.2359， 当网格单元的X5取值=0时， 倾向于M的取值=0；X5的取值>0时， 倾向于M的取值>0。以上结果表明X5与M相互独立的原假设不成立， 两者存在正相合关系。X4与M的列联分析检验p值为4.67×10-184， 相合系数为0.3718， 当网格单元的X4取值=0时， 倾向于M的取值=0；X4的取值>0时， 倾向于M的取值>0。以上结果表明X4与M相互独立的原假设不成立， 两者存在正相合关系。X3与M的列联分析检验p值为8.854×10-34， 相合系数为0.1389， 当网格单元的X3取值=0时， 倾向于M的取值=0；X3的取值>0时， 倾向于M的取值>0。以上结果表明X3与M相互独立的原假设不成立， 两者存在正相合关系。X2与M的列联分析检验p值为7.139×10-83， 相合系数为-0.03289， 当网格单元的X2取值=0时， 倾向于M的取值>0；X2的取值>0时， 倾向于M的取值=0。以上结果表明X2与M相互独立的原假设不成立， 两者存在负相合关系。X1与M的列联分析检验p值为9.26×10-106， 相合系数为-0.03371， 当网格单元的X1取值=0时， 倾向于M的取值>0；X1的取值>0时， 倾向于M的取值=0。以上结果表明X1与M相互独立的原假设不成立， 两者存在负相合关系。

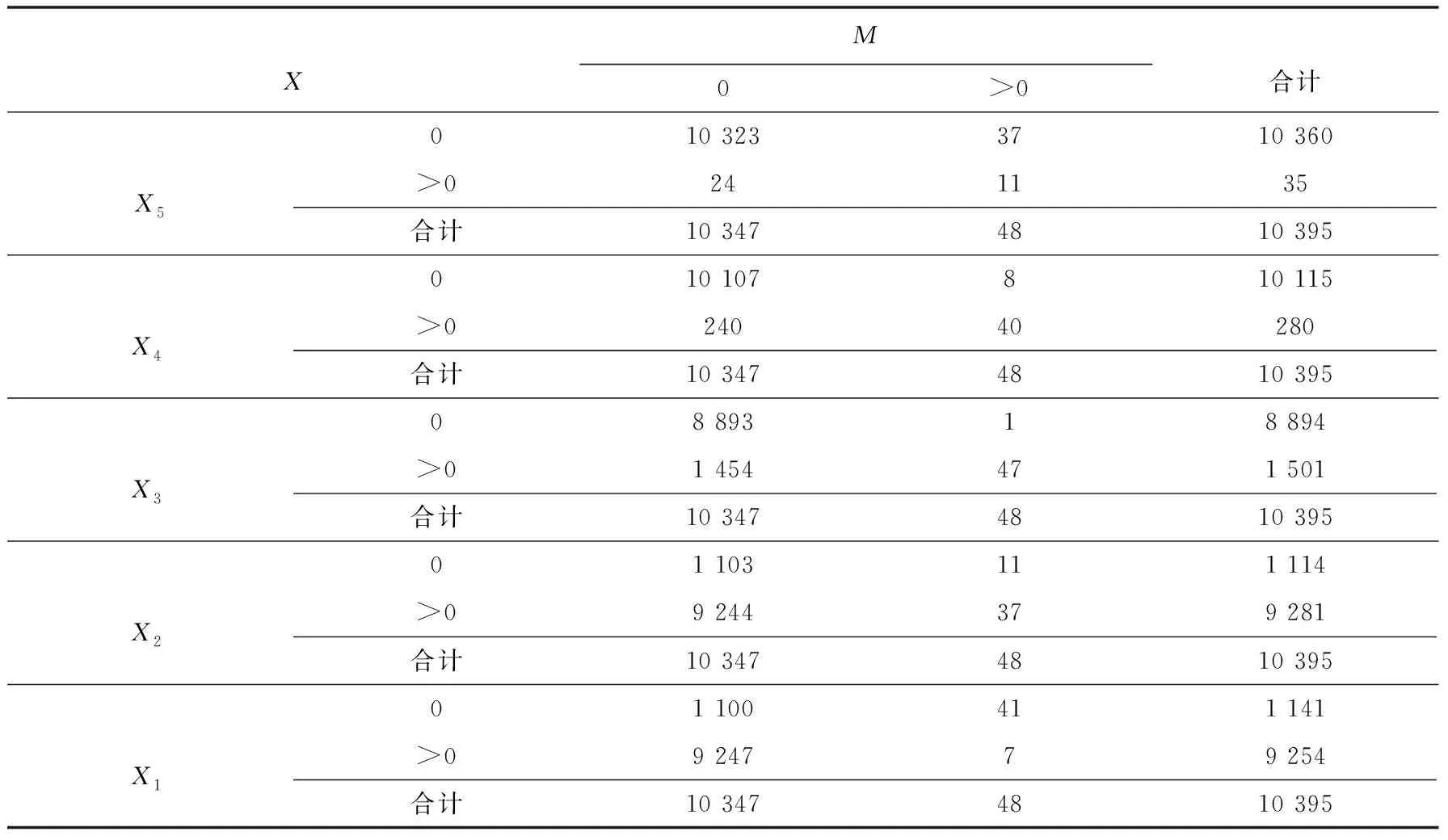
表4 X与M列联表Table4 Contingency table about X and M

从列联表分析结果看， 每组的检验p值都远<0.001， 表明地震滑坡致死率与影响因子相互独立的原假设不成立， 即公里网格单元的地震滑坡致死率与地震滑坡危险性属性相关。从相合系数看，X5、X4、X3与M有显著的正相合关系， 网格单元内属性值为5、 4、 3的地震滑坡危险性像元增加时， 公里网格单元的地震滑坡致死率倾向于>0。X1、X2则与M的增长有显著的负相合关系， 网格单元内属性值为1和2的地震滑坡危险性像元增加时， 公里网格单元的地震滑坡致死率倾向于=0。

2.4.2 地震滑坡致死人数评估模型

从鲁甸研究区的10395条样本数据中选取表3 内的44条数据外再随机选择3001条没有地震滑坡人员死亡的数据作为训练集， 进行基于公里网格单元的地震滑坡致死人数logistic建模， 并用其余的7350条数据作为测试集对所建立模型进行合理性检验。从比例来看， 训练集数据约占样本总数的30%， 测试集数据约占样本总数的70%。我们通过R软件的Newton方法对式(9)中的最大值点和未知参数k、a0、a1、a2、a3、a4、a5进行求解。将软件输出结果代入式(3)， 得到地震滑坡致死率与地震滑坡危险性属性的logistic回归关系：

(11)

式(11)即为针对公里网格单元的地震滑坡致死率计算模型。从回归的公里网格单元地震滑坡logistic致死率模型看，X5和X1的系数绝对值较大， 表明地震滑坡危险性属性最高和最低的像元数量变化对公里网格单元地震滑坡致死率影响较大； 其中，X5的系数最大， 表明公里网格单元内滑坡危险性属性为5的像元数量增加对网格单元地震滑坡致死率增加的贡献最大，X1的系数最小， 表明公里网格单元内滑坡危险性属性为1的像元数量增加对网格单元地震滑坡致死率趋于0的贡献最大。死亡率模型中，X5、X4、X3的系数分别为0.04077、 0.03130、 0.01365， 说明公里网格单元内属性值为5、 4、 3的滑坡危险性像元数量增加则网格单元的地震滑坡致死率增大， 属性值越大的像元数量对网格单元致死率增大的贡献越大；X2、X1系数分别为-0.01666、 -0.09652， 说明公里网格单元内属性值为2和1的滑坡危险性像元数量增加则网格单元的地震滑坡致死率减小， 属性值越小的像元数量对网格单元致死率减小的贡献越大。为了评估该模型的有效性， 我们对训练集和测试集分别进行了F测试值计算。F值越大， 则模型拟合度越好， 模型解释数据的能力越强， 理论上， 只有当F≥0.5时模型才通过检验。在R软件中， 通过>1-pchisq(hp.logit$deviance， hp.logit$df.residual)语句对训练集和测试集的F值进行计算， 输出结果均为[1]1， 即F=1。这表明， 地震滑坡致死率是地震滑坡人员致死性的良好指标， 同时也进一步表明， 所建立的模型可用于公里网格单元的地震滑坡致死率计算。

结合式(10)和式(11)可推导出基于公里网格单元的地震滑坡致死人数评估模型， 简化后的模型表达式为

(12)

用式(12)对鲁甸研究区训练集的地震滑坡致死人数进行计算， 训练集中实际因地震滑坡致死的人数为135人， 模型检测结果为129人， 模型计算的地震滑坡致死人数的精度为95.55%； 对鲁甸研究区测试集的地震滑坡致死人数进行计算， 测试集中实际因地震滑坡致死的人数为115人， 模型计算结果为104人， 模型计算的地震滑坡致死人数的精度为90.43%。对整个研究区而言， 鲁甸地震中因滑坡而死亡(含失踪)的灾民共有250人， 模型检测结果为233人， 误差率为6.80%。

我们通过计算鲁甸研究区各公里网格单元实际的地震滑坡致死人数与模型评估结果的Kappa系数评估所建立模型的统计学意义。计算网格单元的Kappa值时， 将每个网格的总人数拆分为2部分， 即地震滑坡致死人数和其他人数。鲁甸地震灾区的Kappa值为0.912， 表明模型计算结果与实际几乎完全一致， 地震滑坡致死人数计算模型具有较好的统计学意义。从评估死亡人数空间分布(图9a)和实际地震滑坡致死人数的空间分布(图6a)来看， 两者也具有较高的空间分布一致性。

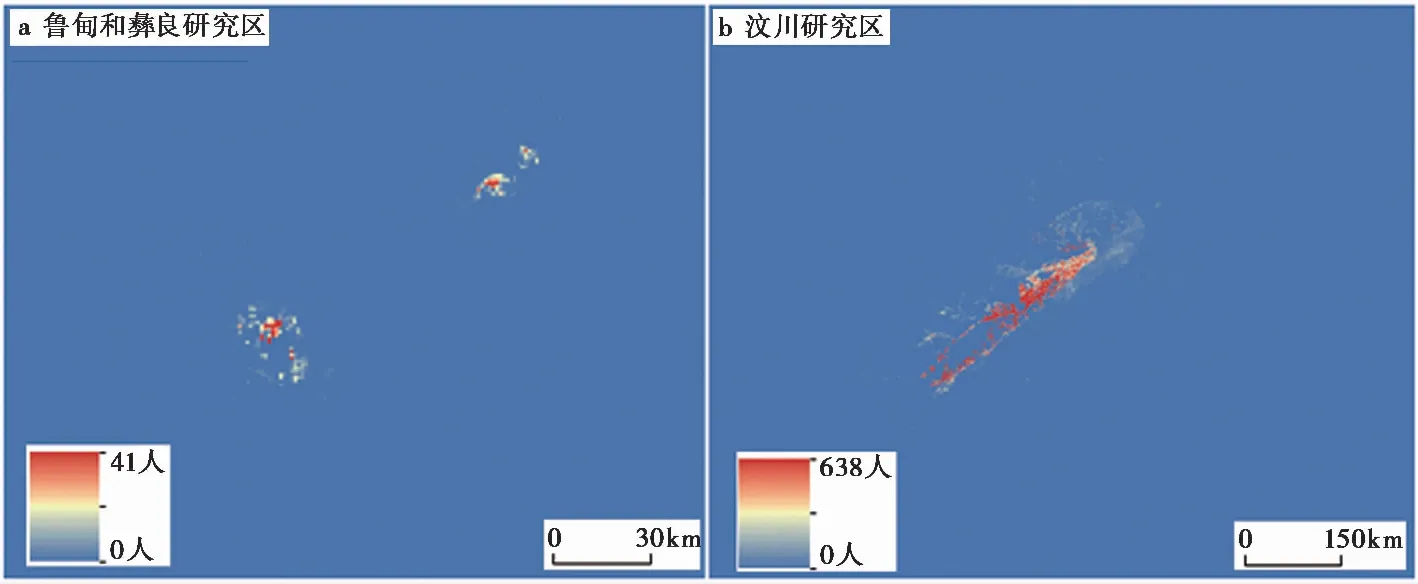
图 9 研究区公里网格地震滑坡致死人数空间分布反演Fig. 9 Inversion of earthquake-induced landslides casualties using GIS and the logistic method.

2.5 模型在汶川和彝良研究区的应用

以汶川和彝良地震灾区为研究区域， 对该方法的外延性及其在更大区域范围的适用性进行检验。将2.4.2节中建立的地震滑坡致死人数评估模型应用到彝良和汶川研究区时， 对评估的方法流程、 模型的参数等均不做任何改动。汶川地震滑坡致死人数的模型评估结果为18732人， 与汶川地震时因滑坡死亡和失踪约20000人的统计结果(Chenetal.， 2011)相比约少千余人， 误差率约为6.5%。此外， 汶川地震公里网格单元的地震滑坡致死人数的空间分布(图9b)与滑坡分布比较一致。由于缺乏汶川地震研究区具体人员死亡地点信息， 故不再计算地震滑坡致死率的F值及各公里网格单元地震滑坡致死人数的Kappa检验值。彝良研究区地震滑坡致死率的F检验值为0.893， 虽然比鲁甸研究区的检验值低， 但其结果仍能满足统计学要求， 模型能够通过数学检验。彝良研究区实际因地震滑坡致死59人(白仙富等， 2014)， 用本文的地震滑坡致死人数评估模型计算结果为死亡48人， 误差率为18.64%。通过对比可知， 各公里网格单元死亡人数的评估结果(图9a)与实际地震滑坡致死人数分布(图6a)仍比较一致， 彝良研究区各公里网格单元地震滑坡致死人数的Kappa检验值为0.889。彝良地震中因滑坡而死亡的人员有半数以上为外地户口在矿区的务工者(白仙富等， 2014)， 而这些外地户口的人员数量只有部分被统计到对应的公里网格单元中， 这是彝良地震滑坡致死人数相比另外2个研究区的评估误差率较大的原因之一。

从基于GIS和logistic模型的地震滑坡致死人数评估方法在汶川和彝良研究区的测试结果看， 本文建立的地震滑坡致死人数快速评估模型在允许一定误差的前提下， 可以用于估计其他区域因地震滑坡灾害导致的人员死亡数量， 具有较好的外延适用性。

模型估计的3个研究区的地震滑坡致死人数都比实际地震滑坡致死人数偏低， 造成这一现象的原因与建模样本数据和选用的方法都有一定关系。用于建模的鲁甸地震灾区样本数据中， 因地震滑坡有致死人数的网格单元数量远远小于致死人数为0的网格单元数量。建模时， 在算法上不仅要考虑的有人员死亡的样本的准确性， 还必须考虑没有人员死亡的样本的正确率。从另一个角度看， 模型对没有人员死亡样本的预测的正确率远高于对有死亡样本预测的正确率。如果减少没有地震滑坡致死人数的样本数据进行建模， 则可能导致死亡人数的评估结果超过实际致死数量， 从而带来另一种误差， 这种误差是所基于的统计方法对于数据驱动固有的不足带来的。在调试鲁甸地震灾区模型的过程中发现， 选取无死亡人数区域和有死亡人数区域的数据分别为3001条和44条样本进行建模是总体误差最小的一种搭配。从模型评估结果的具体数据看， 对3个研究区的评估结果在数量级上都没有偏差， 与实际地震滑坡致死人数也比较接近， 能满足当前应急评估等工作的大部分需求。

3 讨论与结论

显然， 公里网格单元的地震滑坡致死率与90m地震滑坡危险性数据属性之间的相关性是本文建立地震滑坡灾害致死人数判断模型的关键。如前文所述， 本文模型的成立需要2个条件： 1)地震滑坡致死人数评估对象的尺度是1km×1km的网格单元； 2)所使用的地震滑坡危险性数据是90m×90m分辨率的分等级数据。后者又包括2个条件： 1)地震滑坡危险性数据是以烈度为地震动影响参数的产品数据； 2)地震滑坡危险性等级从低到高分为5个等级， 相应的像元的属性值为1～5。当地震滑坡致死人数评估的基本单元尺度发生变化时， 本文提出的这种方法的效果可能会出现变化； 同样， 如果使用的地震滑坡危险性数据不是危险性分级数据或不是90m分辨率的数据， 本文所建立模型的有效性也同样会发生变化。

在地震滑坡致死人数评估方法建立中， 我们考虑了针对公里网格单元的地震滑坡致死率与地震滑坡危险性属性之间的关系。这种关系可用不同模型描述， 本文使用了logistic模型建立地震滑坡致死率与地震滑坡危险性属性之间的关系， 不同类型的模型将带来不同的评估效果， 如何开发不同的模型并筛选出更有效的模型是一个亟待解决的问题。

通过对鲁甸、 汶川和彝良3个研究区进行的方法构建与应用的初步尝试表明， 本文提出的针对公里网格单元的地震滑坡致死人数快速评估方法是有效的， 且在其他多山区域的地震损失评估中也可能具有一定的应用前景。同时， 该方法本质上是一种统计方法， 当样本数量越多或研究区范围越广时， 该方法评估结果的误差可能越小； 相反， 如果研究区的地震震级越小或范围越狭窄， 由于人员在空间分布上固有的动态变化等偶然性因素的影响， 用该方法评估的地震滑坡致死人数的相对误差可能存在更大的离散性。

本文提出的地震滑坡致死人数评估方法是对现有地震地质灾害致死人数评估方法存在缺失现状的一种探索性研究， 尝试在地震后快速地定量化评估地震滑坡导致的死亡人数。在历史地震滑坡致死数据的丰富性、 基础数据的现势性、 模型方法的多样性等方面， 都存在一定的不足之处， 需要在今后进一步发展和完善。

致谢审稿人为本文提出了宝贵的意见和建议； 云南师范大学史正涛教授为本工作提供了支持； 昭通市防震减灾局贺莉晶老师在野外人员死亡地点调查工作中予以协助， 李春博士为本文工作提供了帮助。在此一并表示感谢!