露天矿山采-排动态运输数学模型研究*
2021-12-06彭永根陈诗墨
彭永根,陈诗墨
(1.四川创安太平科技有限公司, 四川 成都 644000;2.西南科技大学, 四川 绵阳市 621010)
0 引言
露天矿生产过程的本质是大规模土石方的空间移运过程,即将地壳的某一部分以一定的时间和空间顺序采掘出来,将有用的物料(矿物)和暂时无用的物料(剥离物)分别搬运至预定地点:矿物运往选矿厂或冶炼厂,剥离物运往排土场[1-3]。露天矿山的一项主要工作就是排土工作,排土工序是露天矿开采的基本工序之一,作为露天矿山接纳废石的场所,是露天矿组织生产不可缺少的一项永久性工程建筑[4-7]。露天矿排土的成本在很大程度上影响了一个矿山的经济效益,对于选择汽车运输的大型露天矿,排土运输费用占整个露天矿生产费用的60%以上。而且随着开采深度的不断增大,这部分费用也在不断增加。为此,许多从事露天采矿的生产者和研究人员一直在深入研究影响运输费用的因素,并寻求解决的对策。研究结果表明,运输卡车台班作业时间只占70%,非生产时间占30%。无论从平面位置还是从立体空间上,各采掘带到排土场各受土部位的运距不同,排土成本也各不相同。为了制定出最经济的排土方案,必须将采区及排土场从空间上划分为规模适中的采掘带及排土带,并验算各采掘带到各排土带的经济性,最终求出最佳的物流规划路径,以获取较好的经济效益。排土优化研究一直是矿山开采优化的一个重要内容, 也是可行性研究、设计和管理的重要组成部分[8-11]。目前,国内外针对露天矿采掘场的研究成果颇丰,基本涵盖了露天矿采掘场相关的所有方面,而针对露天矿排土场的研究成果相对单一,其研究成果绝大多数都是关于排土场边坡工程,关于露天矿排土场综合优化方面的研究较少。
1 问题分析
排土过程与采掘过程不一样,两者的顺序和时空关系刚好相反,排土过程必须先排下面后排上面,先排里面后排外面,只有这样才能形成一个一个台阶,最终堆置成完整的排土场。而露天矿的采掘过程必须是先采上面后采下面,先采外面后采里面。所以在一般工艺下,露天矿前期是采场上部岩土排弃在排土场底部,后期是采场深部岩土排弃在排土场上部,这就很容易造成上土下排、下土上排的情况,在一定程度上影响了露天矿的经济效益。为了使露天矿岩土排弃经济合理,必须进行排土规划。排土规划的最终目的是在采掘场的开拓运输系统已经确定的前提下,排土场的排弃系统应达到经济合理的运输距离,全部剥离排土的贴现值最小。同时,排土规划还应考虑排土场的位置、数量、容量以及对环境的影响。
为达到降低工程成本的目的,常常在排土之前需设计土方调配方案以指导排土工作,凭借以往的工作经验制订方案虽然也有可能得到一个比较满意的效果,但当问题复杂时单凭经验就很难得到最优方案。建立一个动态规划模型就能较好地解决这类问题。
在排土场的设计时,不仅要对排土场进行平面规划,还应对排土场进行竖向规划。以往的排土场分区优化模型都是将排土场和采掘带分区,对每个采掘区运到每个排土区的运输量进行规划,用最小的运输距离和费用来衡量是否最优。把分区排土问题转换成简单的运输问题而求得最优解,这样就没有把实际上废石采掘和堆置受时间和空间的限制因素考虑进去。在实际排土过程中,废石采掘是有一定的顺序的,废石堆置也必须按一定的顺序进行,只有按从下到上、从里到外的顺序堆置,才能使废石堆放有序进行,并保证排土场的安全。
鉴于排土场分区优化涉及到采掘区与排土区之间流量、流向、各采掘区到各排土区的运输距离以及采掘和排土的时间与空间顺序,需要建立一个既能满足各采掘区与各排土区之间排土量的要求,又能满足采掘和排土的时空关系,使总的运输功最小的动态规划模型,利用线性规划或计算机编程求得最优解,为露天矿山排土工程提供优化设计方案,减少矿山排土成本,从而提高矿山的经济效益。
2 建模过程
2.1 排土场与采场分区
将排土场和采场分区并编号,排土场按照堆置顺序从下往上分为i排,从里往外分为j竖,总共分为i×j个排土区,采场按开采顺序从上往下分为k个分区。排土场和采场分区情况如图1和图2所示。

图1 排土场分区示意

图2 采场分区示意
2.2 基本假设
基于实际情况,作如下假设:
(1)采掘区与排土区都是逐一采掘和排土的;
(2)各采掘区的土方量和排土区容量以及各采掘区到各排土区的运输距离可以通过测量和计算得出;
(3)采场排土方量与排土场受土方量平衡;
(4)忽略自然和人为等其他因素对排土过程的影响。
2.3 模型原理
排土场堆排顺序由分区的空间位置所决定,在排土过程中各分区只能按照先里后外,先下后上的顺序堆置废石。显然A11分区是第1个排土区域,只有当A11分区排土完成后才可以选择A12和A21两个分区任意堆排,这也就是说在Aij分区未排完土的时候,对Ai(j+1)和A(i+1)j两个分区的排土在理论上是不可行的,因此在建模的过程中可以引入一个 0-1变量来控制Ai(j+1)和A(i+1)j两个分区在理论上是否可行,这就排除了求出的最优解与实际排土顺序不符合的情况,从而解决以往类似模型不能考虑废石采掘,和堆置受时间和空间限制的问题,同时也保证了排土场排土作业的安全。
采场的开采顺序由开采设计方案确定,对于露天矿山来说,采场开采必须从上往下开采,本文只讨论逐层开采的情况,只有当采场第Bk采场分区采完以后,才能对第Bk+1采场分区进行开采。这就在时空上保证了采场开采的有序进行。
通过采场排土方量与排土场受土方量的运输平衡建立一个简单的运输问题模型,附加一个限制采场开采与排土堆置顺序的动态约束条件,从而建立一个露天矿山采-排动态运输数学模型,既保证了运输平衡,又用动态约束的形式控制了采-排顺序。
2.4 模型所用的变量及含义
基于采-排动态运输的基本假设和需要,建立模型所用变量,其含义如下。
f:排土过程中总运输功或运输距离。Bk:采场第k采场分区。Sk(k=1, 2, …,l):采场第Bk采场分区的排土方量。Aij(i=1, 2, …,m;j=1, 2, …,n),表示排土场第i排第j竖排土分区。Sij(i=1,2,…,m;j=1,2,…,n),表示排土场第Aij排土分区的受土容量;xijk(i=1, 2, …,m;j=1, 2, …,n;k=1, 2, …,g),表示采场第Bk采场分区运到排土场第Aij排土分区土方量;cijk(i=1, 2, …,m;j=1, 2, …,n;k=1,2, …,g),表示采场第Bk采场分区运到排土场第Aij排土分区的运输距离或运输费用。
2.5 模型的构造
矿山通过排土分区优化来减少排土成本,就需要以排土过程中总运输功或总运输费用最小为目标函数,即:

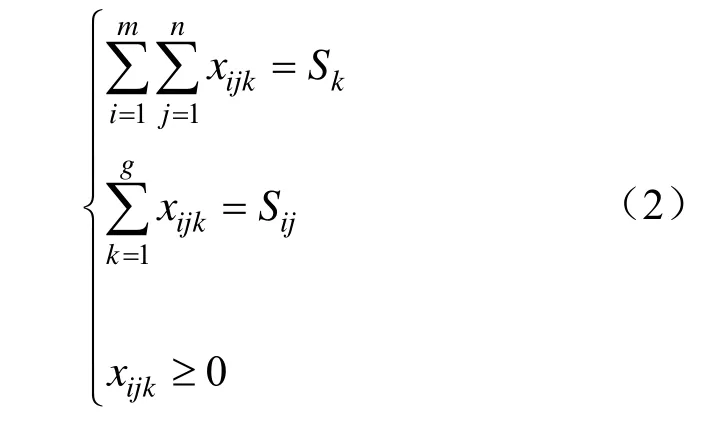
根据采场排土方量与排土场受方量平衡关系可以得出以下约束条件组:式中,i=1,2,…,m;j=1,2,…,n;k=1,2,…,g。
式(2)中分别表示排土场所有分区接受采场某分区的受土方量之和等于采场该分区的排土方量;采场所有分区向排土场某分区的排土方量之和等于排土场该分区的受土方量;及各采场分区运往各排土区的土方量为非负。
这样就建立起了一个简单的运输问题模型,由于废石采掘和堆置均受时间和空间的限制,采掘和排土都必须有一定的顺序,所以露天矿山采-排问题又不是简单的运输问题,需要加入另外的约束条件对采、排顺序加以约束。因此,为了限制废石采掘和排土的顺序,排除与实际排土顺序不符合的情况,可以引入0-1变量:

式中,i=1,2,…,m;j=1,2,…,n。
当各排土区接受采场第Bk分区的排土量之和小于第Bk分区的排土方量时,说明还在开采第Bk分区。当各排土区接受采场第Bk分区的排土量之和小于第Bk分区的排土方量时,方可以开采采场第Bk+1分区。
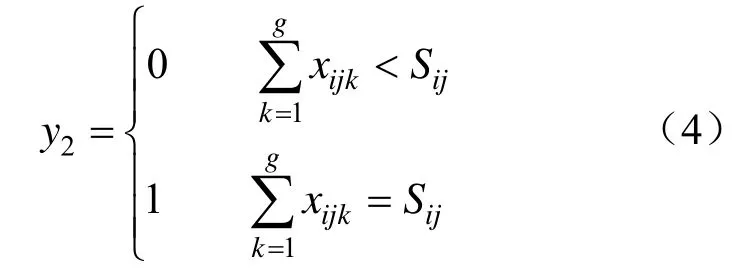
式中,k=1, 2, …,g。
当排土场第Aij分区的受土量小于其土方容量时,应继续向该分区排土;只有当排土场第Aij分区的受土量等于其土方容量时,方可继续向排土场第A(i+1)j分区和第Ai(j+1)分区排土。
此时有约束条件组:
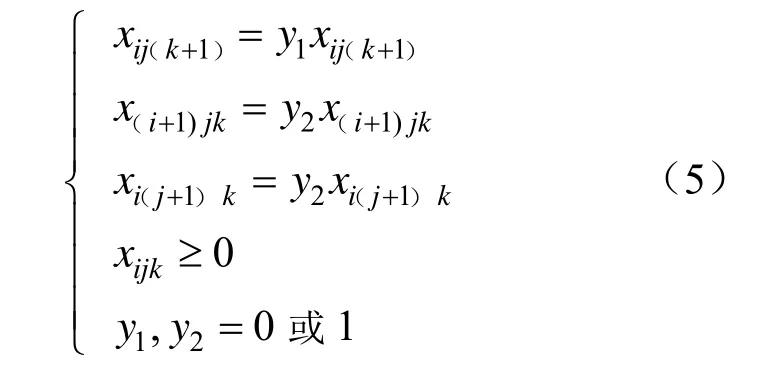
式中,i=1,2,…,m;j=1,2,…,n;k=1,2,…,g。
通过y1来限定采场分区的开采顺序,当上一层分区的土方量采掘完即y1取1时,方可采掘下层分区,排土场相应分区接受其采掘的量就为xij(k+1);而当上一层分区的土方量未采掘完,即y1取0时,采场相对应的下一层分区就不可能开采,相应采掘量为0。
通过约束条件x(i+1)jk=y2x(i+1)jk来限定排土场排土顺序,当排土场分区Aij的受土量与其土方容量相等时及分区Aij排土完毕,相应y2为1,方可向A(i+1)j排土,其接受采场相应分层的排土量为X(i+1)jk;而当排土场分区Aij的受土量小于其土方容量及分区Aij排土还未完成,相应y2为0,就不能向A(i+1)j排土,其排土量相应为0。
通过约束条件xi(j+1)k=y2xi(j+1)k来限定排土场排土顺序,当排土场分区Aij的受土量与其土方容量相等时及分区Aij排土完毕,相应y2为1,方可向Ai(j+1)排土,其接受采场相应分层的排土量为Xi(j+1)k;而当排土场分区Aij的受土量小于其土方容量及分区Aij排土还未完成,相应y2为 0,就不能向Ai(j+1)排土,其排土量相应为0。
综上,建立的动态规划模型是:

其中约束条件组(7)作为模型的最终约束条件。约束条件组(8)和(9)是模型求解过程中的动态约束条件,只作为采-排模型动态控制条件,其结果均是过程量,只对求解过程有影响。
以上模型即为露天矿山采-排动态运输数学模型。模型中包涵了运输问题、动态规划和0-1规划。
3 模型求解建议
该模型不是简单的运输问题,包含了循环求解及动态规划过程,是一个复杂的动态运输模型,可以利用 Matlab软件求解,最后得出最优的排土方案。矿山通过选用优化后的排土方案,不但可以获得可观的经济效益,还可以使国家资源得到了合理的利用。
4 结束语
露天矿山采-排工程是一个复杂的系统工程,本文在对露天矿山采场和排土场合理分区的基础上,建立露天矿山采-排动态运输数学模型,模型结果在保证安全生产的前提下能最大限度的降低露天矿山排土费用,并能充分利用排土场空间,确定出合理排土顺序和最小运输功。该模型具有一定的普遍性。结合实际对排土场堆排方式和顺序因地制宜地进行精心设计,生产程中坚持综合治理,严密管理,可以实现矿山安全生产,达到环保要求,降低生产成本,提高经济效益。
