利用CFD模型改善溢洪道的水力稳定性
2021-12-04王建
王 建
(婺源县水利水电勘察设计室,江西 上饶 334000)
0 引 言
溢洪道和其他泄洪建筑物设计的主要目的是安全地将洪水从大坝输送到下游河道,并防止大坝漫顶,特定类型溢洪道的选择和设计基于项目的特定目的、水文、泄洪要求、地形、地质、大坝安全和项目经济[1-2]。由于提供高效输送水力和结构坚固的溢洪道对大坝的安全以及下游河流的生命和财产非常重要,因此在建造大型大坝时,应对溢洪道的水力稳定性进行检查。检验方法主要可以分为以下两种:水工模型试验和数值模型试验。其中,水力模型试验通过最小化原型来处理流动特性,可以获得相对可靠的结果,因此水力模型被广泛用于解释水力现象的特性。但该方法除了成本较高外,还存在规模效应误差等缺点,因此结合数值模型试验对数学控制方程进行数值分析计算。
通过溢洪道的水流受离心力影响而迅速改变,与逐渐变化的稳定流不同。如果流线弯曲得更陡,水颗粒就不能再沿着流线流动,单独形成一个不连续的部分,包括像水跃一样的快速湍流。对于快速变化的流动,一般的一维和二维数值模拟试验不能直接应用。通过前人的研究可知,三维计算流体力学(CFD)对快速变化的流动和湍流模拟得比较接近原型。如常书平等[3]学者基于计算流体力学(CFD)对喷水推进泵导叶的三维反设计进行研究,主要利用计算流体力学工具建立描述喷水推进泵内流场的数值模型,采用六面体网格划分计算域,选用SST湍流模型封闭雷诺时均方程。喻黎明等[4]学者针对水力旋流器内流场运动复杂、沙粒运动规律难以掌握的问题,运用基于颗粒动力学理论的欧拉-拉格朗日液固多相湍流模型,对水力旋流器内的水沙两相三维流动进行了CFD-DEM耦合数值模拟研究,分析了水力旋流器内单个沙粒的轨迹线、速度和沙粒群的运动规律、分布特性等。黄思等[5]学者运用DEM离散元法结合CFD方法,采用EDEM-Fluent耦合,模拟计算离心泵内非稳态固液两相流动,探索泵内固体颗粒群运动规律及其对外特性的影响。结合前人研究过程,本文采用FLOW-3D模型对初步设计方案中溢洪道内的水流进行模拟,分析溢洪道的稳定性,并解决相关问题。为了验证建模的准确性,将模拟结果与水力模型试验的结果进行比较。
1 FLOW-3D模型
在直角坐标系(X,Y,Z)上,不可压缩三维流动分析的控制方程如下:
(1)
其中:(u,v,w)为坐标(X,Y,Z)方向上的速度分量;(Ax,Ay,Az)为坐标(X,Y,Z)方向上流动开放面积的分数;ρ为密度;RSOR为密度源项。
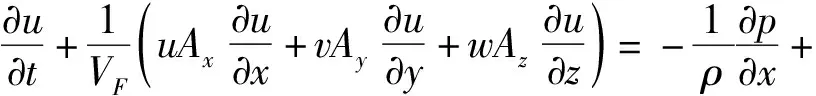
(2)

(3)

(4)
其中:VF为流动开放体积的分数;p为压力;(Gx,Gy,Gz)为坐标(X,Y,Z)方向上的物体加速度;(fx,fy,fz)为坐标(X,Y,Z)方向上的黏性加速度。
为了模拟一个自由表面,即水和空气之间的边界,VOF函数(流体的体积,F)应该满足以下控制方程。如果F(x,y,z,t)等于1,则控制体积中充满流体;如果F等于0,则控制体积中不存在流体。此外,在自由水面的情况下,F值在0到1之间。将函数F应用于式(1):
(5)
2 数值模拟
本文控制方程采用有限差分法离散化,而三维流动采用有限体积法,用有限差分法加上分数面积和体积障碍表示法。通过网格划分分析区域后,基于网格单元进行计算。即可以针对每个网格处给定的压力计算速度,并且使用该速度,算出Poison方程形式的压力方程的值,然后将速度调整到计算值。如果有必要计算自由水面,通常采用固定欧拉法的VOF法。FLOW-3D的VOF方法采用精确的压力和动力学边界条件,并使用特殊的数值差分方法描述两种流体之间的运动,以防止界面模糊。FLOW-3D的网格系统见图1。

图1 FLOW-3D的网格系统
网格和几何图形是构成网格系统的独立元素。一个六面体网格包括结构和墙壁等地形信息(图2)。

图2 分数面积和体积障碍表示法的概念图
除动量方程的压力项和连续性方程的流速项外,控制方程的差分方程可以应用显式差分方法求解。计算时为了满足连续性方程的压力项,可以使用SOR和SADI两种方法。
3 模拟条件
3.1 地形和溢洪道
本研究利用当地实测资料和航空摄影测量绘制出地形图,确定了大坝的地形和溢洪道。确定地形完全覆盖建模范围,包括上游和下游,模型范围见表1。

表1 模型的范围
垂直范围延伸到PMF中超过水库最高水位的范围。图3为大坝和溢洪道的复制地形;图4为溢洪道和引水渠部分。
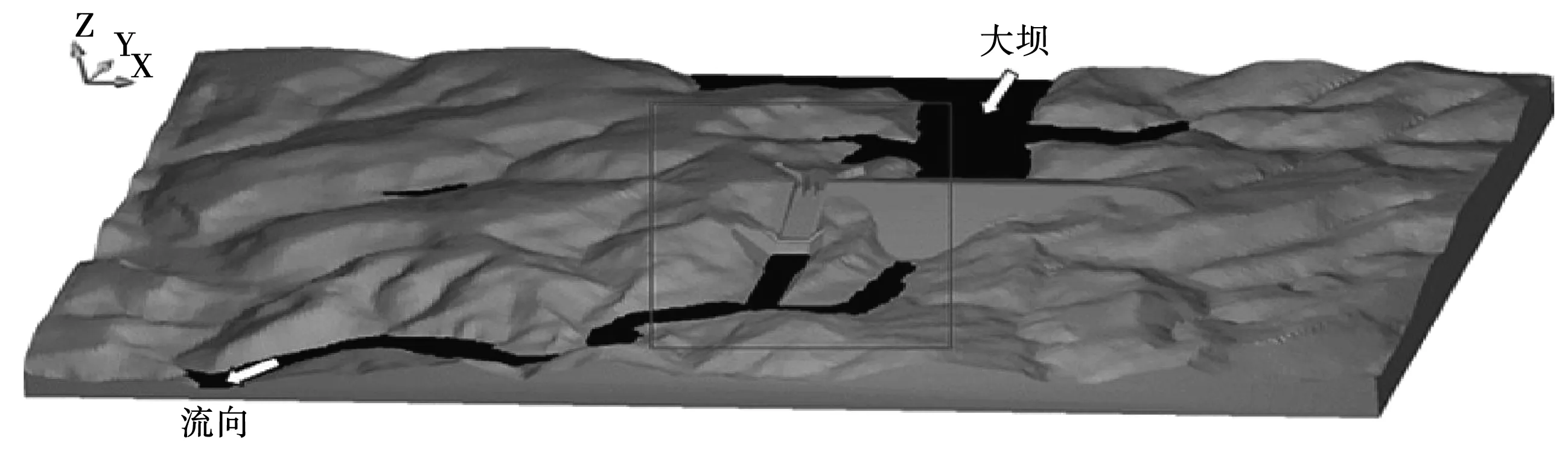
图3 大坝和溢洪道的复制地形
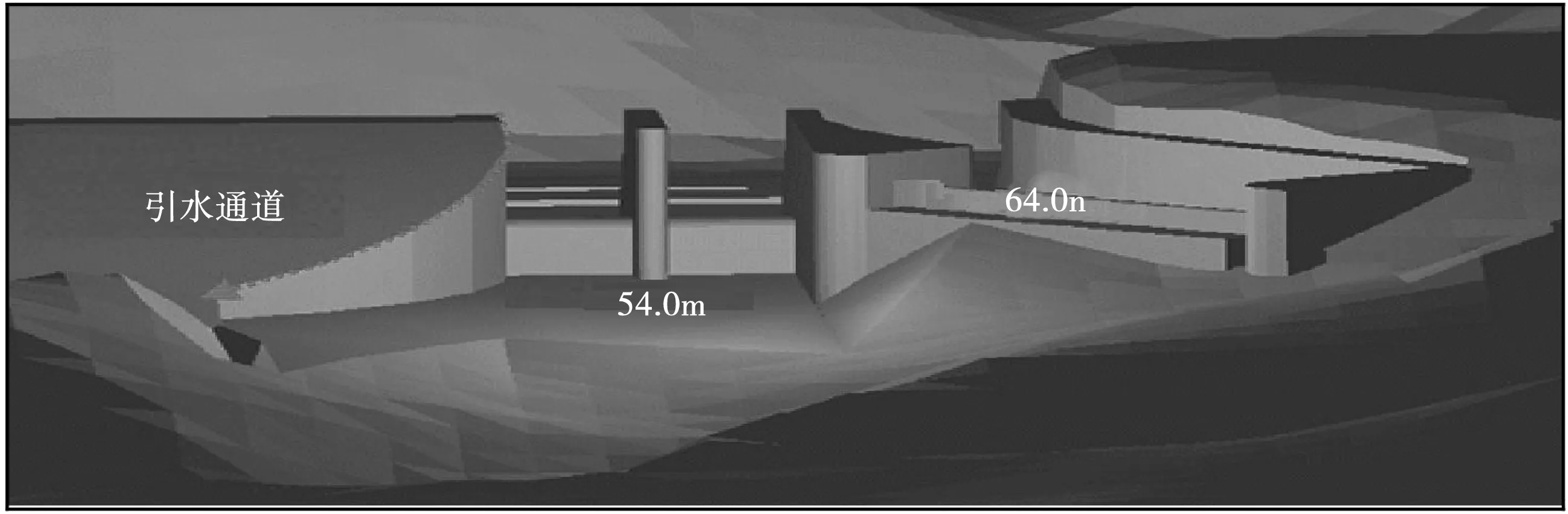
图4 溢洪道和引水渠
3.2 网格组成
采用直角坐标系作为仿真坐标系,并利用航空摄影测量绘制出地形图,将建筑物与复制的三维地形结合,再采用网格法对引水渠的稳定性和溢洪道的泄流能力进行研究。建模是为了在结构(如堰)附近利用粗网格来精确重现流动条件。表2为模拟中使用的网格构成。

表2 网格构成
3.3 边界和初始条件
以上游水库水位为边界条件。对于下游,通过估算精确的水位-流量关系方程,再根据下游河道水位确定边界条件(图5)。由于其余部分为固体边界,为反映壁面的粗糙度,设置为无滑移条件。为了研究溢洪道的稳定性,对侧槽流量和闸门全开度进行检测。对于上游,初始条件定义为上游水库到溢流坝顶的水位相同,流速等所有因变量均固定为零。下游水位的初始水位由下游河道的水位-流量关系曲线确定。
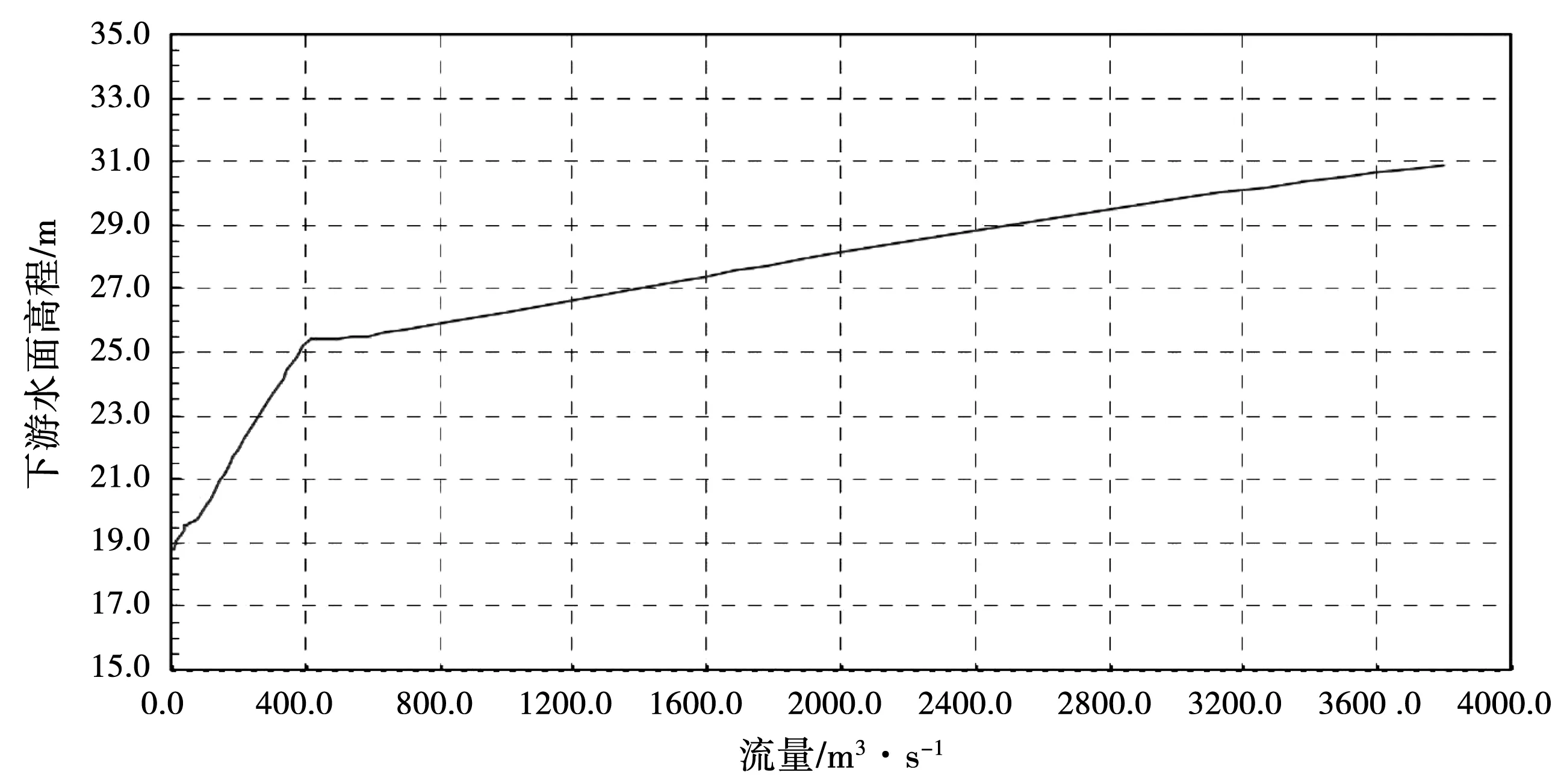
图5 下游河道水位-流量关系曲线
4 结 果
针对引水渠的稳定性,在闸门完全打开时,测量PMF流量和引水渠的流量。图6为引水渠深度为68.12 m时的二维流速分布图,图6中的亮度表示流动速度的大小。
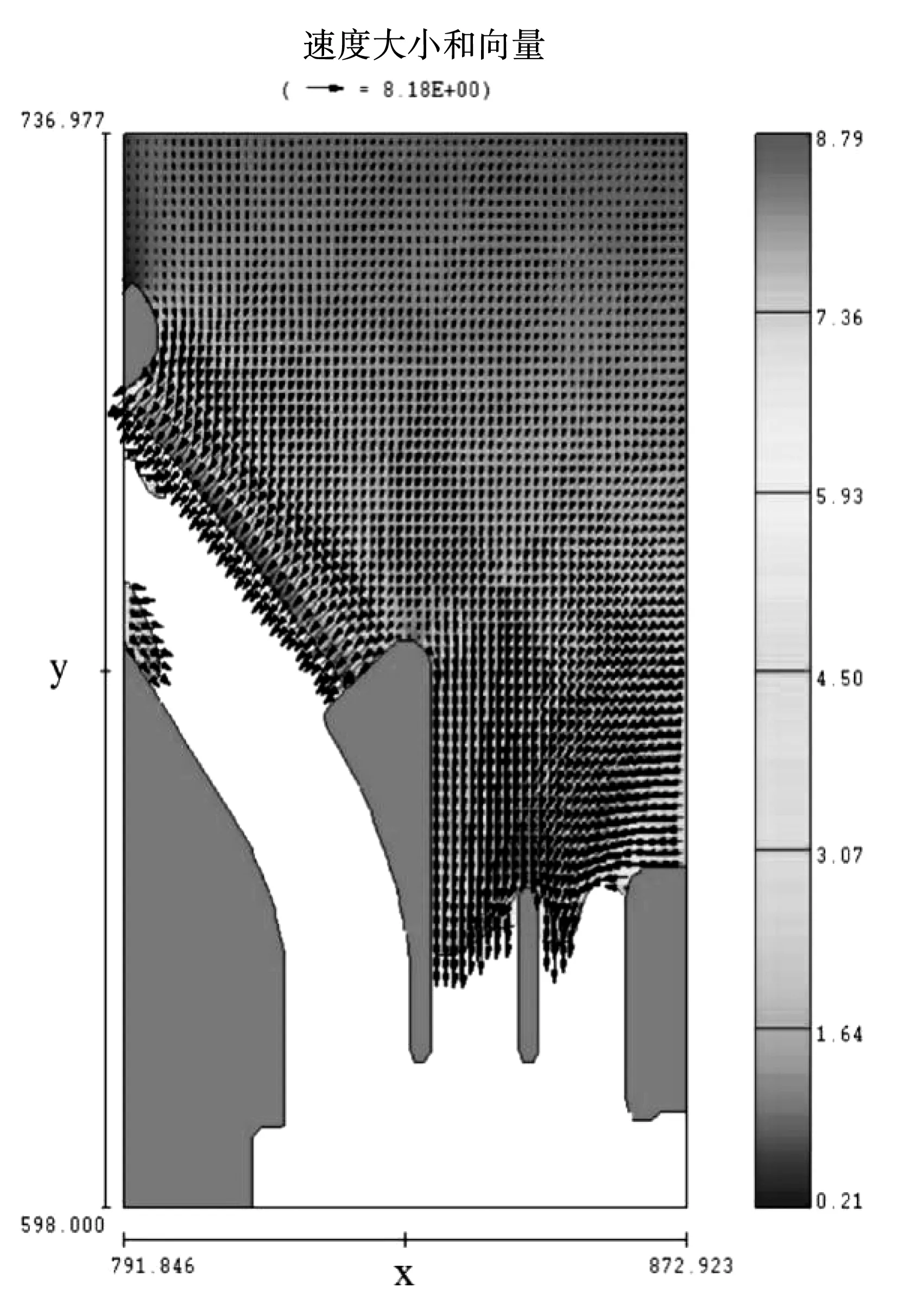
图6 二维流速分布图
引水渠处的水流不应有扰动,故引水渠的设计流量不应超过4 m/s。数值分析结果表明,在PMF中,由于洪水位过高,导致引水渠过墙流动中断。但在设计泄洪过程中,泄洪速度范围为2.0~3.5 m/s。根据现有设计方案的研究结果,存在如下问题:由于高洪水位,水流很可能溢出引水渠墙,并在引水渠处受到干扰而中断。图7显示了PMF泄流过程中引水渠内水流的流动现象,引水通道与大坝上游坡面高程结合时,会出现溢流现象。其中,图7(a)为对应水力模型试验;图7(b)为对应数值模拟试验;图7(c)为横截面视图。
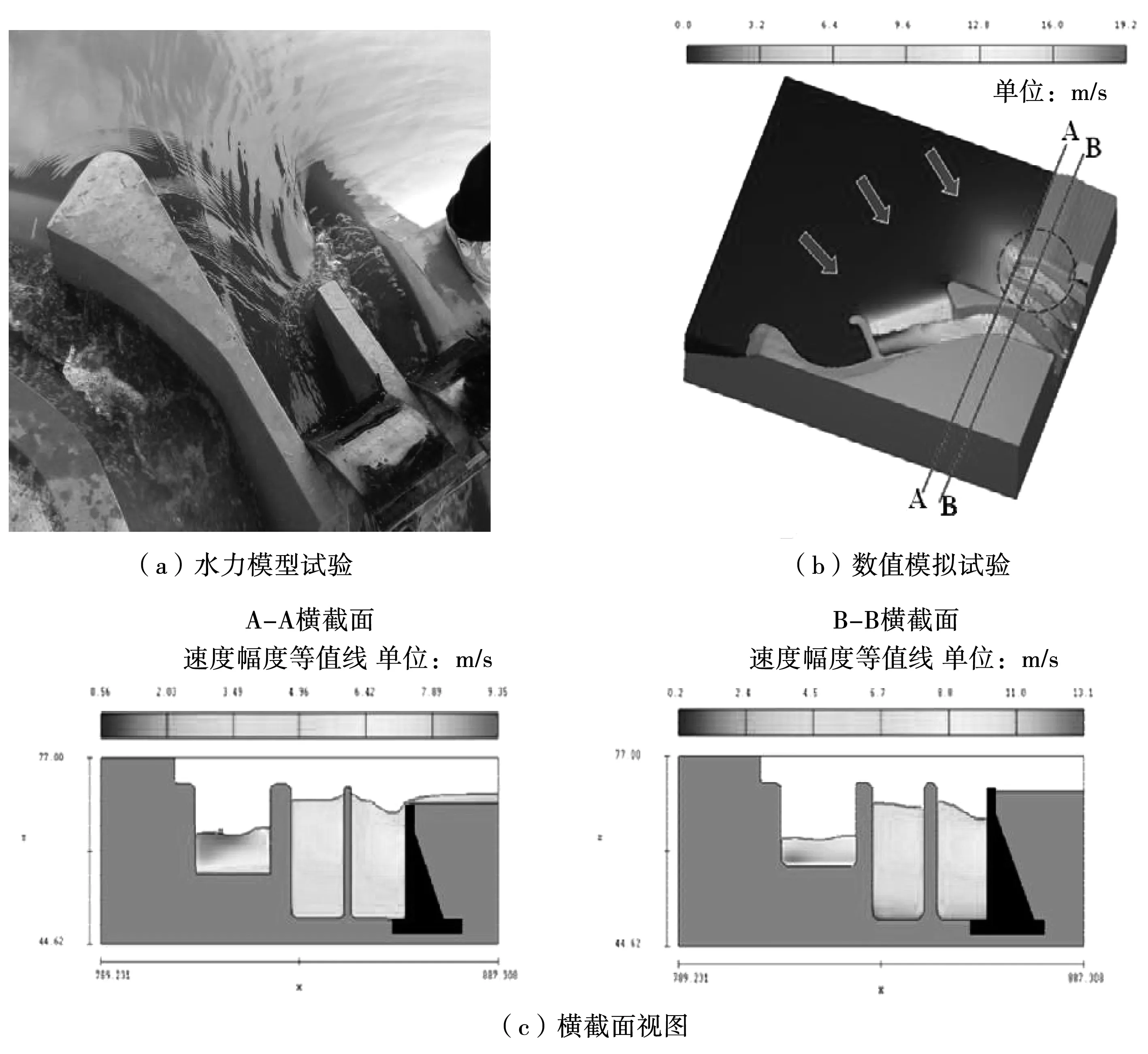
图7 引水渠内的水流流速分布图
由于引水导流壁溢流导致流入不稳定。因此,需要对引水通道进行修改,并通过数值模拟验证修改设计的合理性。为解决以上问题,对原设计方案进行如下修改:①引水通道高度与坝顶高度相等。②曲率半径和长度保持不变。图8为引水渠修改设计方案后的模型,图8(a)对应初步设计方案;图8(b)对应修正后的设计方案。
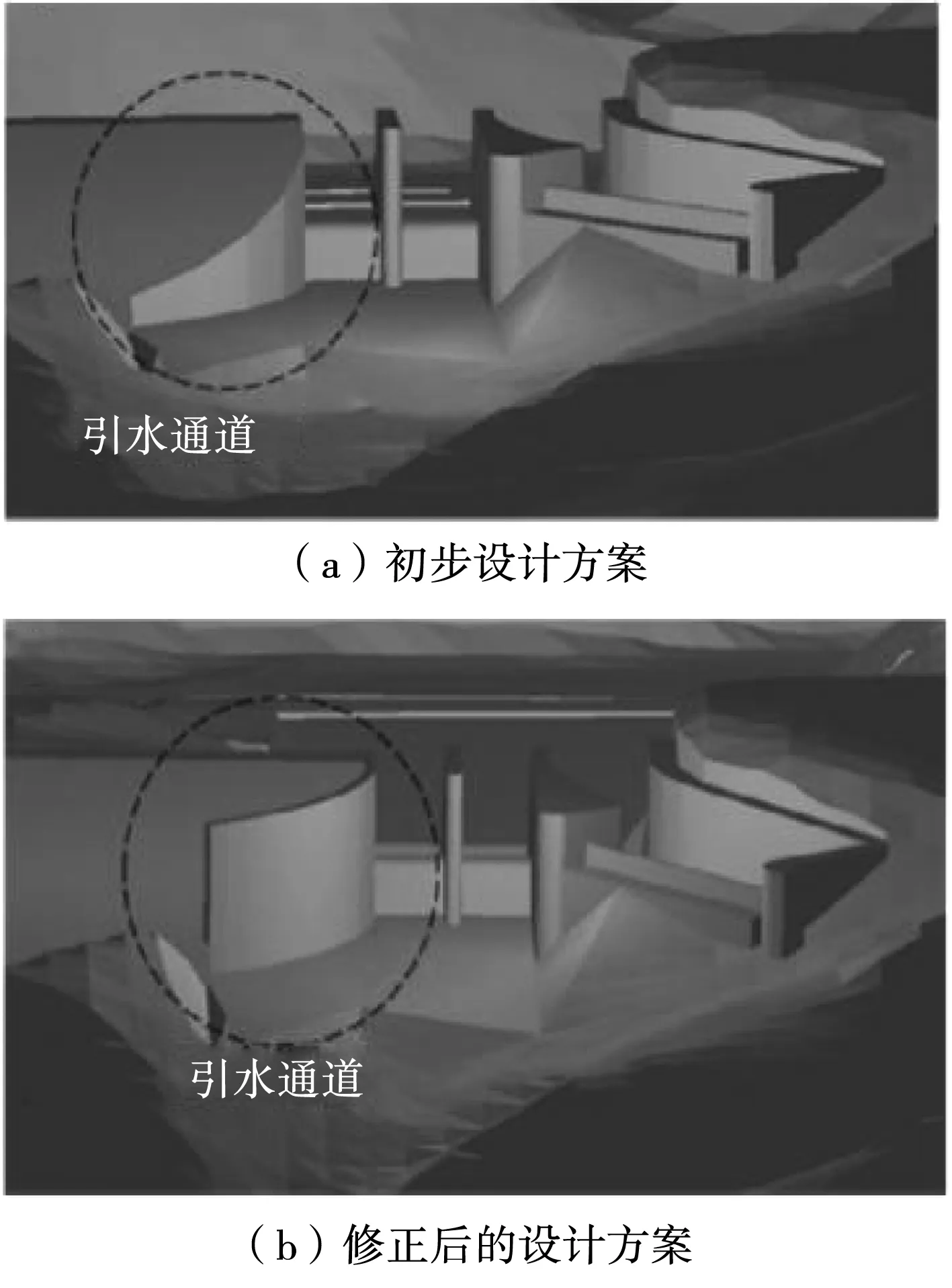
图8 修改设计方案前后的引水通道
基于PMF流量条件,对引水渠处的水流进行研究。图9为修正设计方案后对应引水渠深度为68.12 m处的二维流速分布图。对比图6的流速分布图,发现修正设计方案后,靠近引水通道处的流速减小,溢洪道内水流相对稳定。
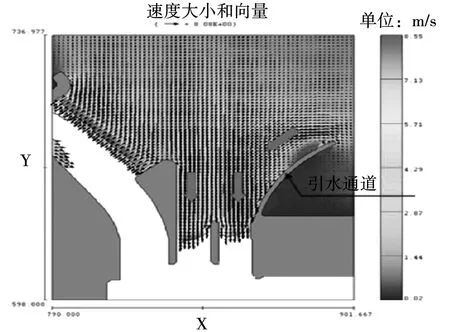
图9 修正设计方案后引水通道对应的二维流速分布图
图10为PMF泄流时引水通道中水流的流动现象,图10(a)对应水力模型试验;图10(b)对应数值模拟;图10(c)对应截面图。结果表明,引水通道处的水流中断现象消失,形成了稳定的水流。

图10 修正设计方案后引水通道对应的流量分配图
5 结 论
为研究溢洪道内的水流和水跃现象,首先采用水力模型试验方法对本文流动现象进行分析。但由于水力模型试验存在规模误差大、费用较高等缺点,所以水力模型试验还需要进一步研究。因此,采用FLOW-3D对溢洪道内水流进行模拟。
1)采用FLOW-3D模型对本文初步设计方案进行模拟。结果表明,在PMF中,水流越过引水渠墙,并在引水通道处被阻断。
2)对初步设计方案进行修改,将引水导墙中引水通道的高度向上调整至与坝顶高度相同。应用修改后的设计方案对溢洪道内的水流进行模拟,结果表明溢洪道内的水流是稳定的。
3)在本文试验情况下,水力模型试验结果和数值模拟试验结果较吻合,说明采用计算流体力学模型模拟溢洪道内的水流是可行的。
