基于遗传算法的道路项目全生命周期优化分析
2021-12-04马文
马文
(山西财贸职业技术学院,山西 太原 030000)
0 引言
工程项目中,工程的工期和成本是高度相关又相互冲突的关系。以往的很多文献研究的成本只考虑建设期成本,没有从全生命周期的角度考虑。一个项目要实现较好的效益,不仅要注重降低建设成本,对于项目未来的维护成本、管理成本乃至拆除成本也要考虑进去,这些成本会直接导致每年的运营成本升高。因此,在工程的工期和成本优化中要全面反映项目的全寿命周期成本。
本文以工期短、全生命周期成本低为目标,将成本分为建设成本、提前投产收益和运营成本三个部分,以各工程项目活动的不同种类模式作为决策变量,建立全过程的多目标优化模型;利用非支配排序遗传算法,求解模型,为实际项目管理提供决策依据。遗传算法求解模型,可得多个最优解,为工程项目管理提供多个最优决策方案。
1 建立模型
各项工程一般包含多项工程活动,本文将每项活动用j 来表示。
每项活动在使用人力、材料、机械设备、施工工艺方法等资源时可以有多种方式,构成了不同的资源调配计划。本文将每一种不同的资源调配计划作为一个模式,用i 来表示。
由于不同的资源调配计划,即不同的模式(i),会影响整个工程项目的工期、费用和质量,所以,将模式(i)作为决策变量。
假设1:每种模式的工期时间都确定,即Tji(i=0,2...,n;j=1,2,...,N)为已知条件。
假设2:项目工期的长短Ti,将影响工程直接成本C直接。如果压缩项目工期,缩减工程使用时间,就需要投入更多其他资源,从而导致直接成本上升。工程实践表明,工程活动持续时间越短,直接成本越高,并且成本增速也会加快[1]。
故采用下式描述其关系。T0为工程活动的正常持续时间,C0为工程的正常成本。

假设3:工程活动持续时间越短,提前投产效益越大,两者呈线性关系。采用下式描述其关系(B1表示活动的最大提前投产效益)。

假设4:关于运营成本,由于建设中的工程活动和建设后的运营成本之间的关系较难描述,我们参照质量指标的描述方式。我们认为工程活动持续时间越长,其质量必然越优,其后期的运营维护成本相应越低;从工程实际表明,由于工艺流程自身瓶颈等原因,随着工程活动持续时间的增加,工程活动对运营成本的影响速度会变慢,使得工程活动对维护成本的影响不可能随时间直线上升。采用下式描述其关系(M0表示工程活动所带来的最低维护成本)。

基于上述式子,可以构造如下优化模型:

式(1)~式(3)中:T为工期总时间;C为建设总成本;M为运营总成本;A为在一个关键路径上形成的活动集合;w为活动i在工程中的权重,表示某一项目活动对未来运营成本的影响程度;
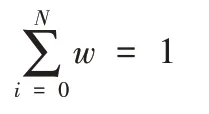
2 模型求解
模型采用多目标遗传算法(NSGAⅡ),引入了快速非支配排序过程、拥挤度的对比和经营策略防止最优单位丢失;可以在一次运行过程中,内在并行搜索,从而获得多个Pareto 最优解,决策者可以从中进行选择[2]。
2.1 染色体编码
本文利用实值编码方法,如图1所示的染色体为单位,用来表示项目工程活动中的一组方案。活动序号由染色体的“基因位”来表示,活动的模式种类用“基因值”表示[3]。

图1 编码方式
2.2 初始化
已知量为每项活动的模式数量:n,那么就在{0,1,2,…,n}内随机产生初始个体的各基因位。种群规模由Nind表示。
2.3 适应度计算
非支配等级和拥挤距离两个因素相互作用,共同决定了每个个体的适应度。个体对应的适应度不是由某个确定的值来表示,而是表现为一个优先级[4]。
2.4 遗传算法
包括选择、交叉和变异三个算子。本模型中选择采用竞赛规模为2 的锦标赛选择法。交叉采用单点交叉操作。
2.5 终止准则
终止准则算法:当进化代数达到最大设定值N时,演化运算结束。
3 算例分析
本文通过以下项目实例来验证模型算法的有效性。在此案例中,共包含七个项目活动,并且这七个活动都在关键路线上,且需要顺序开展,完成前一活动才能进行下一活动。参数如下:种群大小Nind=1000,最大进化代数N=300,交叉概率Pc=0.6,变异概率Pm=0.05。(本例中直接成本已经给出,不通过上文式1 计算,其他项目参数根据式2、式3 求得),如表1所示。
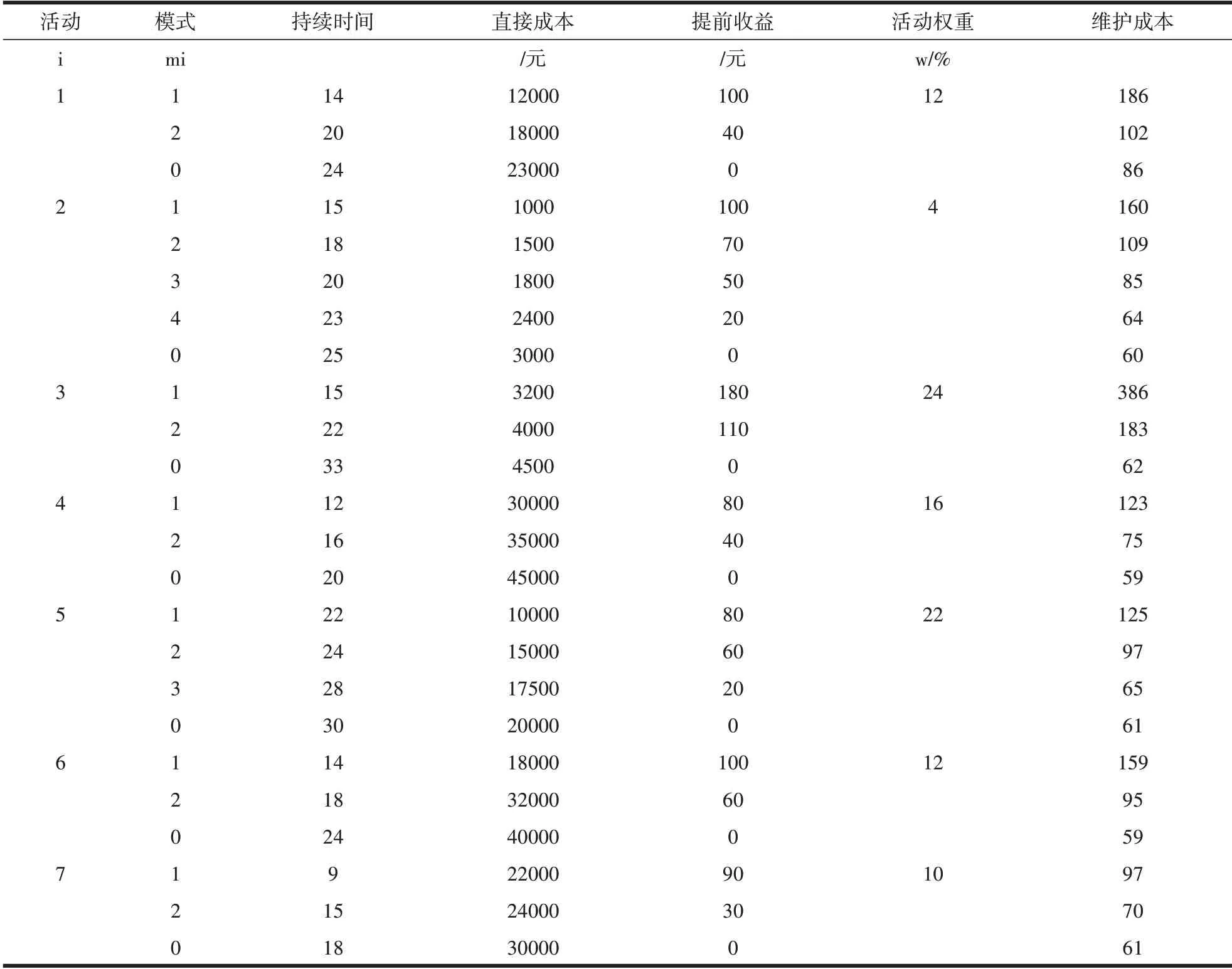
表1 工程活动参数
建立已完工部分的质量评价体系,如图2所示。
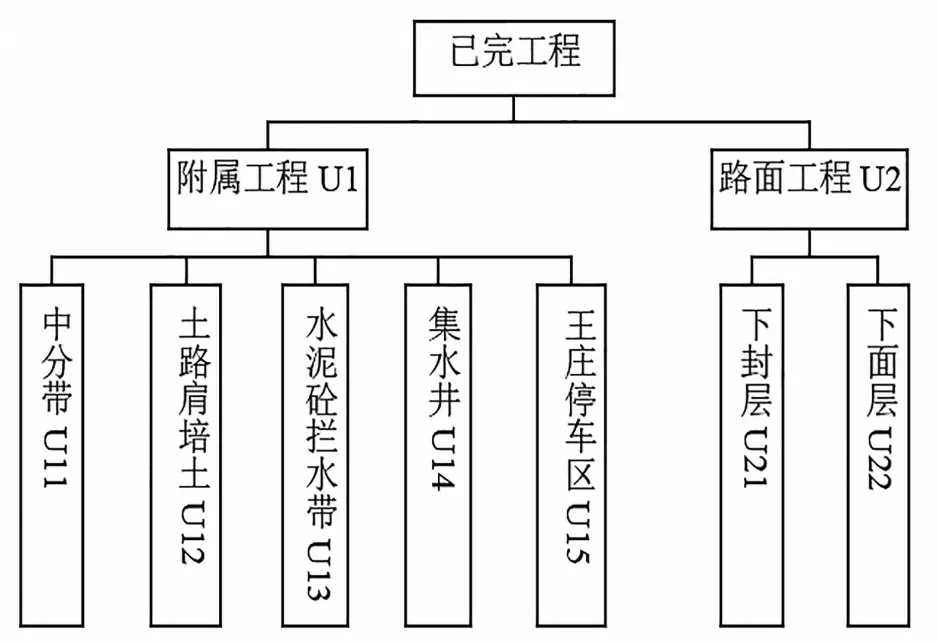
图2 已完工程工作质量评价体系
本工程施工阶段的各项指标计算结果如表2所示。

表2 施工阶段完工工作质量计算表
迭代步骤如下(见图3):
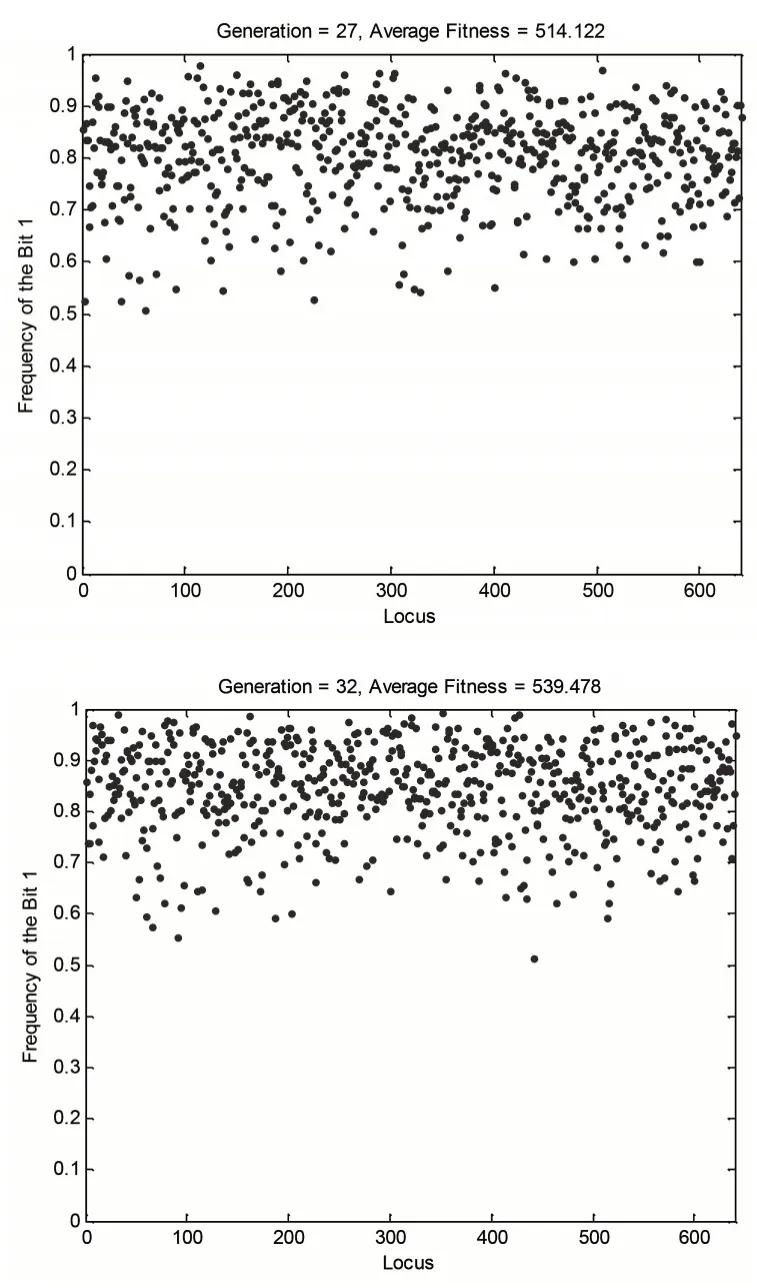
图3 迭代步骤
求得最优解如下(见表3):

表3 项目活动最有组合
成本-工期均衡分析(见图4):

图4 成本-工期均衡分析图
4 结语
从全生命周期成本来考虑工期成本优化,本文主要从两个方面做扩充:一是考虑了提前投产的收益,二是考虑了后期运营成本。这为目前工程项目的成本工期优化提供了新的思路,具有一定的理论意义和实用价值。
