神经网络校正EKF在定位追踪中的应用

部德强

神经网络校正EKF在定位追踪中的应用

部德强

（中国海洋大学 工程学院，山东 青岛 266100）

针对毫米波雷达虽能获取极坐标下目标数据，但无法直接获取目标物位移分量且受系统噪声影响无法进行高精度定位跟踪的问题，提出一种利用反向传播（BP）神经网络校正扩展卡尔曼算法的无人帆船目标物的精确定位方法。通过扩展卡尔曼算法融合毫米波雷达数据，估计动态目标直角坐标系下的位移分量；并用BP神经网络算法校正扩展卡尔曼滤波器，以降低动态目标物运动的不确定性及噪声影响。仿真结果表明，该方法能够降低系统噪声的影响，更准确地进行目标物的定位追踪。

无人帆船目标物；神经网络；扩展卡尔曼；定位追踪

0 引言

随着海洋勘探活动的不断深入，以风力作为驱动的无人帆船，因其具有更低成本、更长航时、更大范围、更高时空分辨率等优势，被越来越多地应用于海上探测活动[1]。当前对无人帆船定位追踪目标物的研究较少，而随着海洋环境的不断恶化，加强对海面漂浮物的追踪研究显得十分迫切，因此本文提出了一种利用无人帆船实现海面目标物精确定位追踪的研究方法。

由于目标追踪的复杂性，直接获取目标物精准定位存在一定的困难。国外提供了很多定位追踪的研究方法[2-4]。国内文献[5]针对传统的定位技术误差比较大，无法预测动态追踪目标的实时位置等问题，提出了一种结合运动方程与卡尔曼算法的动态目标追踪预测算法，有效地提高了定位精度，并对目标位置进行了实时预测。文献[6]提出基于带外源输入的非线性自回归(nonlinear autoregressive with exogenous inputs, NARX)神经网络技术建立了单海况下的预测数据模型，通过船舶仿真器得到了舰船升降仿真模型，将NARX模型与传统卡尔曼模型、反向传播模型的预测结果进行对比，验证了NARX神经网络对复杂海浪环境具有更好的适应性和高海况下的高预测精度。文献[7]针对传统卡尔曼算法的噪声方差不能自适应调节的问题，提出了将模糊控制器加入到卡尔曼算法中，对不同环境下的方差进行修正，适时调整噪声力度，以提高卡尔曼算法的自适应能力与定位系统的抗干扰性。同样针对噪声方差不能自适应调节的问题，文献[8]提出了将反向传播（back propagation, BP）神经网络算法加入到卡尔曼算法中，建立了基于BP神经网络算法和卡尔曼算法相结合的船舶运动跟踪模型，得到了船舶的运动状态，实验结果证明该算法精度高，噪声抑制能力强，可以实现复杂海情下的船舶运动跟踪，但该结果基于系统模型是线性系统的情况下，而现实中目标物的测量值与估计值为非线性关系，传统标准卡尔曼算法不适用于非线性系统。本文将研究更接近实际的非线性系统模型，并通过BP神经网络算法对扩展卡尔曼滤波器（extended Kalman filter, EKF）进行校正，以期提高扩展卡尔曼滤波器的性能，从而提高定位追踪能力。

无人帆船通过全球定位系统（global positioning system, GPS）坐标转换构建平面直角坐标系[9]，使无人帆船与目标物在同一坐标系下。为了更好地实现定位追踪，需要获得动态目标在此直角坐标系下的位移分量，激光雷达可以获取相关数据。但考虑到激光雷达受环境、天气影响较大，无法全天候精准作业，因此本文提出应用扩展卡尔曼算法融合毫米波雷达的数据估计目标物运动参数分量，并用BP神经网络算法校正扩展卡尔曼滤波器，以提高扩展卡尔曼滤波器性能，使得无人帆船对目标物的定位追踪精度得到较大提升。

1 控制系统流程

毫米波雷达在环境感知、目标跟踪、路径规划及自主避障中都发挥了极其重要的作用[10]。将毫米波雷达获得的目标数据作为观测值，输入到扩展卡尔曼滤波器中与估计值融合，扩展卡尔曼滤波器依次完成预测状态值、预测协方差、计算卡尔曼增益、计算估计值、更新协方差5个步骤后将预测误差、新息、卡尔曼增益作为BP神经网络的输入量并进行训练，以估计误差作为神经网络输出，与扩展卡尔曼滤波器输出估计值求和，重新计算最优估计。控制系统流程如图1所示。

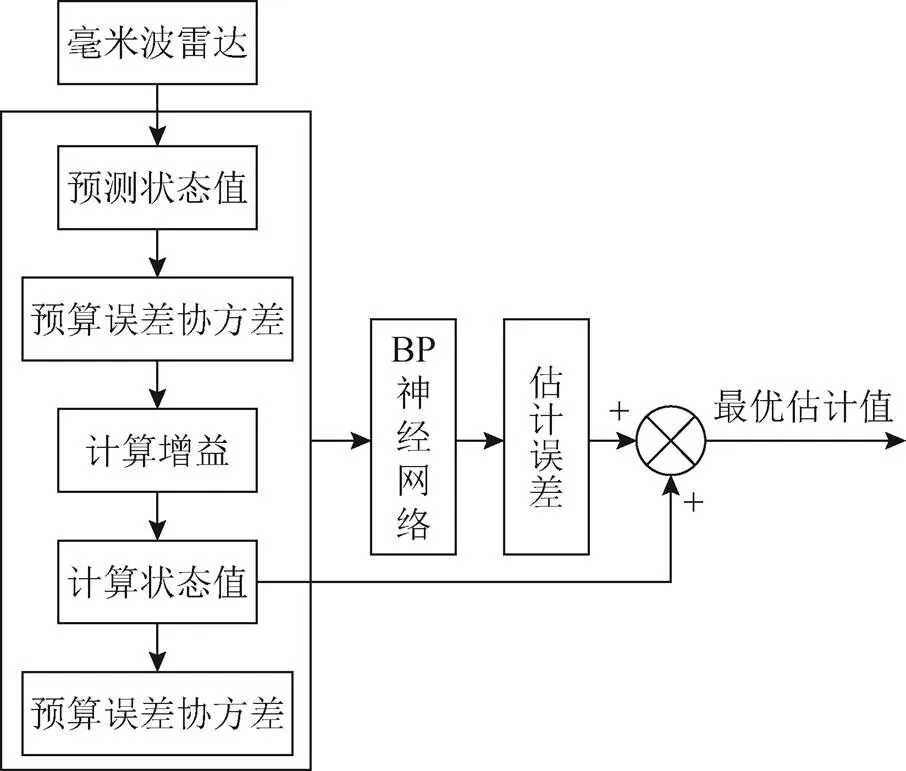
图1 系统控制流程

2 目标物定位追踪算法

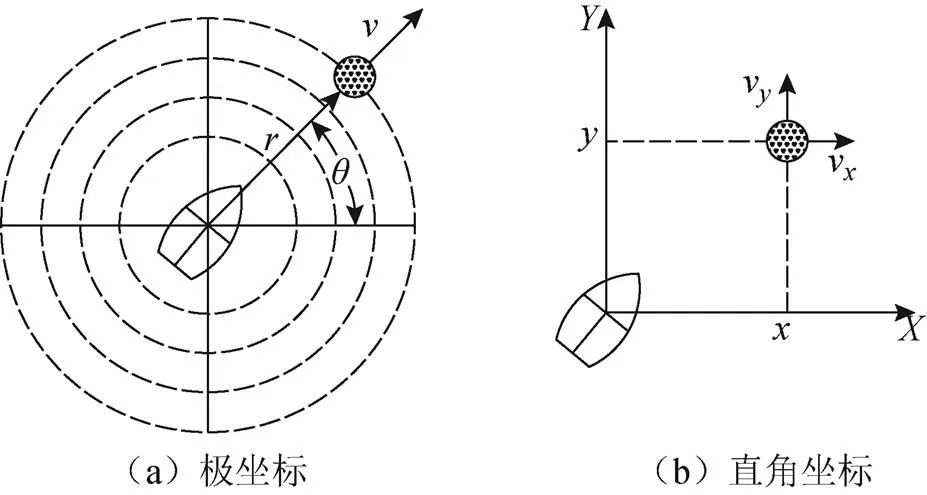
图2 坐标转换

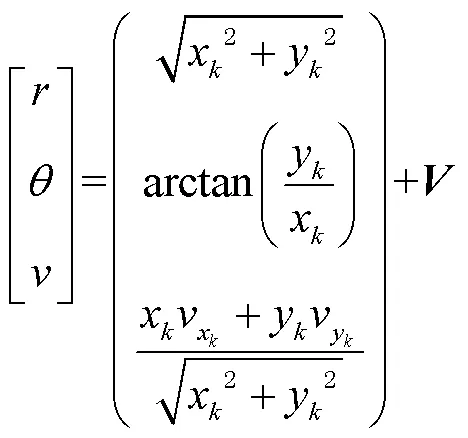
2个坐标系之间的转换关系为

2.1 扩展卡尔曼算法

由式（1）可以看出，目标物的定位为非线性转化过程，扩展卡尔曼算法可适用于非线性系统，首先建立基本系统模型为

泰勒公式可将非线性系统线性化，线性化系统重新利用卡尔曼算法的5个公式估计位移分量与速度分量。卡尔曼算法5个公式为

采用日立 L-8800氨基酸自动分析仪对酱醪中氨基酸进行测定，测定过程委托贵州大学南区分析测试中心，样品预处理采用GB/T 5009.124-2003进行处理。仪器进样时泵1压力为2～15 Mpa，流速为0.4 mL/min，仪器进样时泵 2压力为 0.5～2 MPa，流速为 0.35 mL/min。

2.2 神经网络算法校正扩展卡尔曼算法

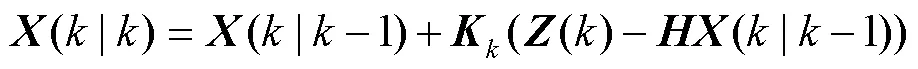
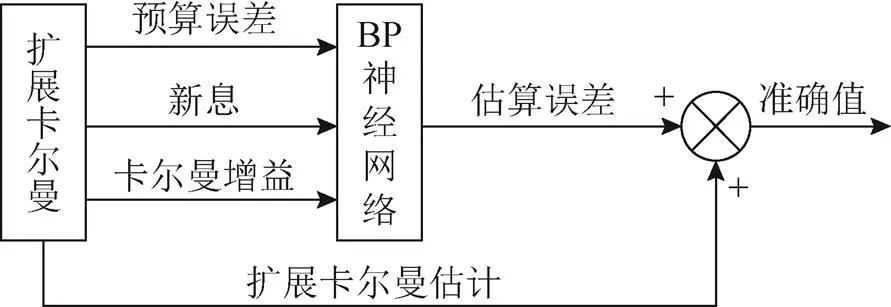
图3 BP神经网络优化EKF原理

确定神经网络的输入输出参数后，须确定神经网络的隐藏层层数和每层结点数。根据以往经验，隐层的数量越多，对系统的非线性映射能力越强，但每层层数过高会导致神经网络计算量过大，学习速度变慢和过拟合等情况[12]。扩展卡尔曼算法中预测误差是4×1维矩阵，新息是3×1维矩阵，卡尔曼算法增益是4×3维矩阵，输出估计误差为4×1维矩阵，由式（7）[13]确定BP神经网络输入层神经元个数为19个。

式中：为估计状态维度；为新息维度。通常设置单层隐藏层且神经元节点个数足够即可无限逼近真实值。为了提高系统的可靠性[14]，本文设置隐藏层的个数为2层。由式（8）[15]可计算出各层隐藏层的神经元个数为[8，8]。

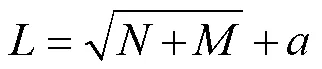
式中：为隐藏层神经元个数；为输出层神经元个数；的取值为（1,10）。

BP神经网络算法的训练过程由信号的正向传播和误差的反向传播2个部分组成。正向传递首先随机初始化权重与偏置，权重的取值范围为[-1, 1]，偏置的取值范围为[0, 1]，然后由式（9）正向计算输出值，进而计算误差损失。

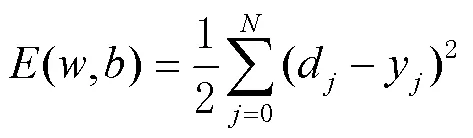
3 仿真与结果分析

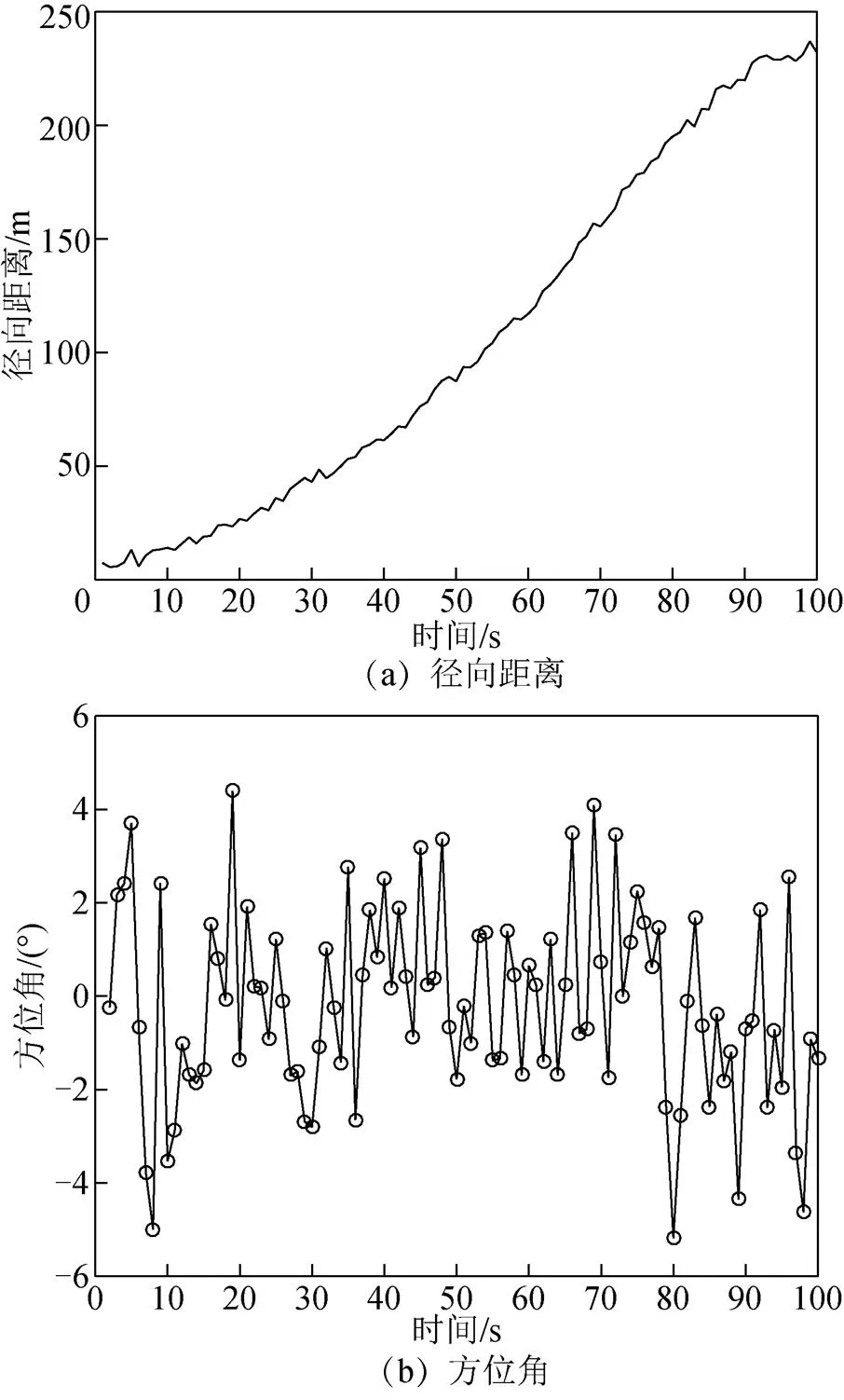
基于以上参数，在MATLAB中得到动态目标物与无人帆船的径向位移图、方位角变化图和径向速度变化，如图4所示。

扩展卡尔曼算法与BP神经网络扩展卡尔曼（BP-extended Kalman filter, BP-EKF）算法通过融合毫米波雷达数据可以获得动态目标物的位移分量。2种算法的定位轨迹仿真如图5所示。由图5（a）可以看出扩展卡尔曼算法可以通过融合毫米波雷达数据完成动态目标的定位，但与图5（b）BP神经网络扩展卡尔曼算法的定位轨迹相比，在非线性较强的转弯段出现相对较大误差，误差最大可到5 m左右，且在较为平缓的直线段也存在一定误差。图5（b）中，经过BP神经网络算法校正的扩展卡尔曼算法定位轨迹精度大幅度提高，无论在非线性较强的转弯部分还是直线部分，定位轨迹基本逼近期望数据，精度较高。

图5 EKF、BP-EKF仿真对比

为了验证BP神经网络对扩展卡尔曼算法的校正作用，仿真另选取非线性较强的有交叉形态的动态目标物轨迹，如图6所示。在图6（a）中，扩展卡尔曼算法在交叉轨迹附近，滤波器不稳定出现不收敛趋势且定位误差变大；在图6（b）中，BP神经网络扩展卡尔曼算法定位更加稳定，且定位精度更高。

图6 EKF、BP-EKF交叉形态轨迹仿真对比

为了验证仿真数据的可靠性，经过多次仿真实验统计分析，得到2种算法轨迹的横向位移平均误差与纵向位移平均误差，如图7所示。从图7（a）、图7（b）中可以看出：扩展卡尔曼算法轨迹的横向位移平均误差与纵向位移平均误差在0.8 m范围内，而BP神经网络扩展卡尔曼算法横向位移平均误差与纵向位移平均误差在0.2 m范围内，精度提高较为明显。

图7 EKF、BP-EKF平均误差对比

4 结束语

无人帆船追踪目标的过程中，为了得到目标物的坐标位置，更好地实现目标物的定位追踪，本文提出对毫米波雷达获得的数据用扩展卡尔曼算法进行融合，同时用BP神经网络算法对滤波器进行校正，来估计目标物的位移分量。

本文在MATLAB中建立目标物的系统模型，通过对比扩展卡尔曼算法与BP神经网络优化扩展卡尔曼算法2种情况下得到的位移分量，经误差分析得出：扩展卡尔曼算法能实现目标物的实时追踪，但在复杂路况下有误差变大的可能性；BP神经网络校正扩展卡尔曼滤波器的算法，误差小、可靠性高，性能优于单一扩展卡尔曼算法。加入神经网络的扩展卡尔曼算法定位精度虽然得到提升，但如果神经网络算法计算量大，将导致系统效率降低，因此本算法还可深入研究优化。

[1] 俞建成, 孙朝阳, 张艾群. 无人帆船研究现状与展望[J]. 机械工程学报, 2018, 54(24): 98-110.

[2] CHIN L. Application of neural network in target tracking data fusion[J]. IEEE Transactions on Aerospace and Electronic Systems, 1994, 30(1): 281-287．

[3] VAIDEHI V, CHITRA N, CHOKKALINGAM M, et al. Neural network aided Kalman filtering for multitarget tracking applications[J]. Computers & Electrical Engineering, 2001, 27(2): 217-228.

[4] JARADAT M A K, ABDEL-HAFEZ M F. Non-linear autoregressive delay-dependent INS/GPS navigation system using neural net-works[J]. IEEE Sensors Journal, 2017, 17( 4): 1105-1115．

[5] 王妍, 邓庆绪, 刘赓浩, 等. 结合运动方程与卡尔曼滤波的动态目标追踪预测算法[J]. 计算机科学, 2015, 42(12): 76-81.

[6] 楼梦瑶, 王旭阳, 陈瑞, 等. 基于NARX神经网络的船舶升沉运动实时预测方法[J]. 中国舰船研究, 2020, 15(1): 48-55.

[7] 柏菁, 刘建业, 袁信. 模糊自适应卡尔曼滤波技术研究[J]. 信息与控制, 2002, 31(3): 193-197.

[8] 朱广华. BP神经网络和卡尔曼滤波相结合的船舶运动跟踪[J]. 舰船科学技术, 2016, 38(20): 82-84.

[9] 肖体琼, 陈怡群, 常春. GPS经纬度坐标转平面坐标的简化计算方法及精度分析[C]//中国农业工程学会. 中国农业工程学会学术年会论文集. 广州: 中国农业工程学会, 2005: 49-52.

[10] 庄加兴, 焦侬, 殷非. 毫米波雷达与激光雷达在无人船上的应用[J]. 船舶工程, 2019, 41(11): 79-82.

[11] HAYKIN S. Neural network principle[M]. Beijing: China Machine Press, 2004．

[12] 丁一, 张瑶, 李冠男. 神经网络校正的EKF在水下被动目标跟踪中的应用研究[J]. 小型微型计算机系统, 2020, 41(5): 897-901.

[13] 董志荣, 苗艳, 李艳丽. 目标定位和跟踪的卡尔曼滤波加BP神经网络的方法[J]. 火力与指挥控制, 1998，23(1): 3-5.

[14] 白宇骏, 徐晓苏, 刘国燕. 神经网络辅助卡尔曼滤波技术在组合导航系统中的应用研究[J]. 中国惯性技术学报, 2003,11(2): 42-45.

[15] 赵明, 何书前, 石春, 等. 一种基于神经网络修正参数的卡尔曼滤波室内定位方法[J]. 现代电子技术, 2020, 43(7): 21-24.

[16] 李忠利, 刘小锋, 陈修魁, 等. 基于信息融合的拖拉机组合导航定位系统研究[J]. 农业机械学报, 2020, 51(8): 382-390.

Application of neural network-aided EKF in localization and tracking

BU Deqiang

（College of Engineering, Ocean University of China, Qingdao, Shandong 266100,China）

Aiming at the problems that the millimeter-wave radar can obtain the target data under polar coordinates, but it can’t directly obtain the displacement component of the target object, and it is also unable to carry out high-precise location tracking due to the influence of systematic noise, the paper proposed a precise positioning method of unmanned sailboat target object using an extended Kalman algorithm aided by Back Propagation (BP) neural network: the extended Kalman algorithm was fused with the millimeter-wave radar data to estimate the displacement component of the dynamic target in Cartesian coordinate system, and the BP neural network algorithm was used to correct the extended Kalman filter for reducing the motion uncertainty of the dynamic target and the influence of noise. Simulational result showed that the proposed method could help reduce the influence of system noise, and achieve accurate target localization and tracking.

unmanned sailboat target object; neural network; extended Kalman; localization and tracking

P228

A

2095-4999(2021)06-0084-06

部德强. 神经网络校正EKF在定位追踪中的应用[J]. 导航定位学报, 2021, 9(6): 84-89.（BU Deqiang. Application of neural network-aided EKF in localization and tracking[J]. Journal of Navigation and Positioning, 2021, 9(6): 84-89.）

10.16547/j.cnki.10-1096.20210613.

2021-01-18

部德强（1991—），男，山东济南人，硕士研究生，研究方向为海洋机电装备与仪器。