基于Taguchi 方法的三相混合式步进电机电磁结构优化
2021-12-03方玲利肖龙飞
方玲利,肖龙飞,毕 超
(上海理工大学 机械工程学院,上海 200093)
混合式步进电机(Hybrid Stepping Motor,HSM)诞生于20世纪70年代,其具有高分辨率和高转矩密度,可实现开环控制,且无累计步距误差,被广泛应用于众多领域,例如各种办公自动化设备及数控机床系统等[1]。市场上现有的混合式步进电机按其定子绕组数目可分为两相、三相和五相。其中两相混合式步进电机(2P-HSM)占据了大部分的市场份额[2-3]。究其原因,主要有两点:(1)历史因素。自第一台2P-HSM问世以来,为抢占市场份额,研究人员把精力集中在2P-HSM的设计和控制上。相较于其它HSM,2P-HSM的电机本体优化及驱动控制技术最为成熟;(2)相对2P-HSM,其他混合式步进电机的电磁结构更为复杂,涉及的电磁分析及优化设计难度更高,耗时也更长。
理论上,相对于2P-HSM,三相混合式步进电机(3P-HSM)整体性能更为优越,主要表现在:(1)定位精度更高;(2)振动和噪音更小;(3)控制成本更低等[4]。因此,从长期应用及效益来看,3P-HSM有更好的发展空间,对3P-HSM的电磁结构进行优化设计具有重要意义。
3P-HSM最重要的组成部分是齿层结构,HSM产生和机电能量转换均基于定转子的齿槽效应[1,5]。因此,选择最佳的齿层几何形状是设计优化过程中的首要任务。在过去的几十年中,众多学者对于HSM的齿部形状提出了各种不同的观点,例如矩形、三角、梯形和圆形等[6-8]。本文基于3P-HSM内部电磁现象,对齿形进行重新分析,发现梯形齿对气隙磁密的影响程度更大,且包含更多的形状参数,更适用于电机电磁结构优化。
对齿形形状优化的困难之处在于,HSM为双凸极磁层结构,转子表面多齿,初始模型的小齿数达50个,且需考虑到转子双向(轴向和径向)励磁原理,因此电磁结构非常复杂。针对3P-HSM复杂的工作原理,简化的线性模型及等效磁路法等都无法做到精确计算[4-11],必须采用3D磁场的数值分析手段对其进行磁场分析。该方法借助麦克斯威尔方程组和变分原理,将复杂的电磁场问题转化为能量泛函求极值问题,即多维代数方程组的求解[10]。本文采用3D有限元法(Finite Element Method,FEM)对3P-HSM进行实体建模及仿真。利用试验有限元方法得到电机的磁场信息后,在计算过程的后处理部分对电机的转矩进行计算。
3D-FEM精度高,但计算量非常大,这使得许多全局优化方法,例如传遗传算法,粒子群算法等,获取目标样本的时间变长,无法估计所需投入的时间成本[12-14]。Taguchi算法通过局部优化,能在最少的试验次数内(即构建最少的有限元模型)利用离散数据找到最佳组合,大幅度削减了时间成本。
本文将Taguchi优化算法与3D有限元模型相结合,对市场上某款3P-HSM进行优化设计。通过优化该款3P-HSM齿形结构提高电机产生电磁转矩的能力,从而改善电机的性能。最后,对比样机测试结果证明了该优化方法的高效和正确性。原始样机(Initial 3P-HSM)的初始结构如图1所示,具体结构参数见表1。

表1 3P-HSM的部分参数Table 1. Parameters of 3P-HSM
1 3P-HSM的有限元模型
3P-HSM作为典型的三维高度饱和非线性系统,必须采用3D磁场的分析手段,即有限元法(Finite Element Method,FEM)。FEM是目前场量计算方法中精确最高,适用性最强的一种数值方法,被广泛应用于电机电磁场的计算分析[1]。为了获取更为精准的矩角特性,本文借助FEM,建立3P-HSM的3D有限元模型,如图2所示。通过合理配置仿真环境,仿真计算3P-HSM的转矩。核心计算式为
(1)

(a)

(a)
式中,W(θ,i)是磁共能;i为电枢绕组电流。
对于混合式步进电机,设计中最为关键的步骤为设计齿层区域 ,即定子和转子的齿形及电机的气隙,其影响着电机性能。在过去的几十年中,研究人员对步进电机的齿形提出了不同的设计[7]。其中,图3所示的矩形齿获得了最高的市场认可度。然而,实际经验及研究结果表明,图4所示的梯形齿相比于矩形齿更好,这是因为图4所示的形状系数更大,对气隙渗透性的影响大,更适于后期优化。本文为获取更佳的优化成果,以梯形齿的形状系数作为核心优化对象。此外,为了规避3D-FEM计算量大且时间成本高的缺点,本文引进了Taguchi优化算法,通过高效利用离散数据来提高优化效率。

图3 HSM的矩形齿形结构Figure 3.Rectangular tooth structure of HSM

图4 HSM的梯形齿形结构Figure 4.Trapezoidal tooth structure of HSM
2 3P-HSM的齿形优化
为了提高3P-HSM的转矩性能,本文在现有3D-FEM的基础上,结合Taguchi优化算法,优化电机齿形结构,以改善步进电机的矩角特性。
2.1 Taguchi优化方法
Taguchi优化方法由日本质量管理专家田口玄提出,是目前日本工业界提升品质的最佳方法之一。作为一种局部优化设计方法,Taguchi优化算法擅长使用离散结果来探索最佳点,即通过最少的试验次数得到最佳优化组合,已被广泛用于国防、化工和电机分析等场合[11]。
该方法的主要流程如图5所示,其中Taguchi正交表与信噪比是Taguchi优化算法的两大核心工具。前者通过设计具有代表性的试验有效降低实验或仿真所需次数,大幅度削减时间成本,提高了效率;后者则筛选最佳参数水平组合,指引进一步优化方向的重要指标[15-18]。

图5 Taguchi优化流程图Figure 5.The flowchart of Taguchi optimization method
本文将3P-HSM的优化目标函数设定为转矩峰值最大化(Torque-max),即
Torque-max=max(Tpeak)
(2)
式中,Tpeak为矩角特性的峰值转矩。
在Taguchi优化方法中,信噪比的计算涉及以下计算式
(3)
(4)
(5)
式中,n是每个实验重复试验次数;yi是第i次实验的结果;y和s分别代表目标函数的平均值和标准偏差。
针对Torque-max这一优化目标,本文采用式(4)进行信噪比的计算。此外,本文利用式(5)对优化目标THD-min进行计算。以上两个目标的信噪比值均越大越好。
2.2 Torque-max的实现
矩角特性的幅值,即最大静转矩,是评价混合式步进电机性能的重要指标之一[1]。为了实现峰值转矩最大化目标,基于Taguchi优化过程及梯形齿形结构参数,本次优化方案构建了4因子3水平正交实验表。具体的齿形优化参量如表2所示,正交实验表如表3所示。

表2 转矩峰值最大化齿形优化参量Table 2.Torque peak maximization tooth profile optimization parameters

表3 正交实验表Table 3. The orthogonal experiment table
图6为齿形结构因子的主效应图。由图可知,A因子对于转矩峰值的影响最大,B和D因子居中,C因子于转矩的作用十分微弱。根据信噪比均值可判断最佳因子水平组合为A1B1C1D1。鉴于目前电机制造工艺的限制,本文不进行下一阶段优化,即确定该水平组合为样机的最终优化结果,其具体齿形见章节3中图9(c)和图9(d)。

图6 齿层结构因子的主效应图Figure 6.The main effect diagram of tooth structure factor
图7所示为初始3P-HSM(Initial 3P-HSM )和Torque-max 3P-HSM的矩角特性对比图(仿真结果)。可见,相比于初始3P-HSM,Torque-max 3P-HSM的转矩幅值有明显提高。

图7 原型机和转矩峰值最大化样机的矩角特性曲线Figure 7.Torque angle characteristic curve of prototype and torque peak maximization prototype
3 实验测试
试验样机如图8所示。原型机的实际齿形结构见图9(a)和图9(b)。优化后的Torque-max 3P-HSM样机齿层结构见图9(c)和图9(d)。

图8 实验样机Figure 8.The experimental prototypes for HSMs

(a)
搭建实验所用转矩测试平台,如图10所示。合理配置控制参数,通过细分控制结合齿轮箱变速,使得被测电机以极低速旋转1个齿距,并配合11位的光电编码器和高采样频率的转矩传感器,同步输出转矩及角度信号,据此来获取三相混合式步进电机的矩角特性曲线。

图10 转矩测试平台Figure 10.The testing platform of the torque-angle characteristic
对图8所示的两个测试样机进行静转矩测试,实验测试结果如图11所示。由于受谐波影响,电机矩角特性曲线并非正弦,且受二次谐波影响较大。表4表明两台样机转矩峰值的仿真与试验结果十分接近。需要注意的是,有限元仿真更为复杂的梯形齿层结构时,因网格剖分精度的问题,有限元的实际计算结果会有所偏差,导致有限元计算结果小于测试结果(这点与实现 “THD-min”后样机数据现象一致),但趋势和优化方向是正确的,证明了本文建立的有限元仿真模型的准确性。对比数据结果,样机Torque-max 3P-HSM的峰值转矩比原型机初始3P-HSM提高了近25%,实现了转矩峰值最大化的优化目标。
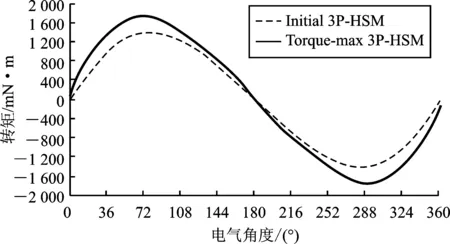
图11 样机矩角特性的实验测试结果Figure 11.The testing results of torque-angle characteristic of the prototype

表4 实验结果与仿真结果的对比Table 4. The comparison between simulation results and testing results
4 结束语
基于对三相混合式步进电机的优化研究,本文提出以梯形齿形状参数作为优化对象,通过结合3D有限元模型与Taguchi优化算法进行电机电磁结构优化,以实现更高的转矩输出。两台样机的仿真和试验结果表明,通过电机齿形结构的优化,混合式步进电机的性能得到了明显提高。与原型机Initial 3P-HSM相比,转矩最大化样机Torque-max 3P-HSM的转矩峰值提高了近25%。本文结果证实,基于3D有限元模型,借助Taguchi方法获取最佳梯形齿形是优化混合式步进电机的有效手段。该优化方案也适用于其它电磁结构的优化。
