基于功能安全分级的起重机智能制动器制动频率区间研究*
2021-12-03孙远韬黄重阳陈凯歌秦仙蓉
孙远韬 黄重阳 陈凯歌 张 氢 秦仙蓉
同济大学机械与能源工程学院 上海 201804
0 引言
制动器作为各型起重机起升和行走机构的核心安全部件,对保障其安全运行起着至关重要的作用。制动器主要有2个功能:消耗载荷的动能和停止载荷的运动。随着起重机的运动惯量和运动速度不断提高,为令制动的中间过程可控,避免制动过急造成传动系统乃至整机结构的损伤,智能型制动器应运而生[1,2]。
主流的常闭式智能型制动器由制动弹簧按压摩擦材料以保持制动器的常闭状态,而电液推动器则通过一支杠杆来压缩弹簧以实现开闭的中间过程,故电液推动器的驱动电机频率决定了制动力的大小。为了保证这种功能复杂多样的新型智能制动器的安全可靠,需要对其功能安全特性进行研究。国际电工委员会曾提出了功能安全的概念,其中SIL[3-5]是IEC61508—《电气/电子/可编程电子 安全系统的功能安全》中的一个重要概念,SIL基于风险和安全的概念展开,SIL越高,系统越安全,风险越低。
制动频率是智能型制动器的核心参数,因而从频率入手以保证其制动可靠性是重中之重。此前,文献[6]提出了一种基于功能安全的起重机安全防护系统设计方法,文献[7] 进一步对这种方法进行了实施,实施对象为起重机用智能制动器。在进行SIL划分时,主要考虑了制动器机械结构静强度的可靠性及失效概率,但智能制动器的运行受到驱动电机的频率波动制约,导致其制动过程中存在可靠性问题。因此,本文基于功能安全设计方法,对某型智能制动器进行制动实验,采集制动力在各频率下的数学分布规律,据此建立功能函数,采用蒙卡方法计算离散可靠度,继而回归失效概率曲线,再根据目标SIL等级,对智能型制动器的频率进行范围优选,建立智能型制动器基于功能安全的最优制动频率范围,进一步保障智能型制动器的可靠性。过程如图1所示。

图1 基于功能安全的优化设计方法
2 常闭式智能型制动器制动实验
2.1 电液型智能制动器
如图2所示,电液型制动器的组成部分包括电液推动器、制动弹簧、闸块、杠杆系等[8]。制动路径为:驱动电机推动电液推动器,继而通过杠杆系统改变对制动弹簧的压力,最终改变制动力。

图2 智能型制动器
当忽略电液推动器活塞与液压缸之间的摩擦时,可知活塞的受力包括制动弹簧和复位弹簧对活塞的力F1(其大小与活塞的行程有关),油液对活塞的推力F2。
油液对活塞的推力F2来自电液推动器,其内部构造如图3所示。下部电动机接通后使联通液压油的叶轮高速旋转,依靠离心力通过液压油推动上部活塞产生推力,此推力即制动器的开启力。改变电机的频率f即可改变它的转数,从而改变离心力的数值,进而改变了推力F2。

图3 电液推动器剖面图
制动器施加在制动盘表面的正压力为

式中:N为制动盘正压力,L为杠杆系统放大系数,m为推杆和活塞的质量。
杠杆系统放大系数为[9]

式中:Me为额定制动力矩,D为制动理论摩擦直径,F为推动器额定推力,μ为摩擦系数,η为机构总传动效率,取0.85,φ为推力利用系数,取0.95。
当F2=0时,制动器处于完全制动状态;当F2>(F1+mg) 时,处于松闸状态;当 0<F2<(F1+mg)时,则处于制动与松闸的过渡状态。
2.2 实验原理及方法
为探究制动力与频率的数学关系,并基于功能安全建立频率优化模型,进行了制动力实验,在实验中,针对YP21LZ-800-630*30型号的5台制动器进行测试。试验中共需记录的数据为额定弹簧预紧力下随频率变化的静态制动力以及最大弹簧预紧力下随频率变化的静态制动力。
如图4所示,试验系统由制动器、变频器、压力传感器(带仪表)以及若干导线组成。由于在试验前期的准备测试中,传感器读数的偏差较大,且传感器很长一段时间未被使用,所以首先需要对试验用压力传感器进行标定,标定使用的校验标准仪器是输出压强可调的油压机,标定后,将传感器夹在制动盘之间进行试验。在制动器预紧弹簧的预紧力矩分别调为额定值和最大值的情况下,通过缓慢增加变频器的频率,改变电机的输入频率(此过程可忽略开启过程中的惯性力),读取此时压力传感器的读数即为此频率下实际的静态制动力的大小。

图4 实验布置图
在实验中,手动打开制动器的制动盘,在制动盘之间放入压力传感器,通过在传感器上添加吊耳以固定其位置。先将制动器的预紧弹簧力矩值调至额定值,从0开始,通过面板按钮,以1 Hz为步长,逐渐调高变频器的输出频率,通过显示仪记录相应频率值的制动力读数,同时记录实时功率作为参考。观测电液推杆运动,当推杆打开时即停止。再从推杆打开频率开始,逐渐降低变频器的输出频率,仍以1 Hz为步长,降至0 Hz,并记录制定力与实时功率。
2.3 实验结果
对额定弹簧预紧和最大弹簧预紧力下的数据进行分析,得出如下数据:
1)同一类型的5个制动器在同一频率下的制动力均值及方差;
2)制动力离散分布规律(固定频率下的制动器制动力的分布规律);
假设制动力的分布服从正态分布频率为f i,5个制动器的制动力均值记为μFi,标准差记为σFi,最大制动力记为Fimax,最小制动力记为Fimin,则固定频率f i下的Fi分布规律可表示为

根据实验结果应分别获得额定弹簧预紧力和最大弹簧预紧力作用下的分布规律,分别记为Fi_rated和Fi_max。
图5为5个制动器的静态制动力与频率关系图。
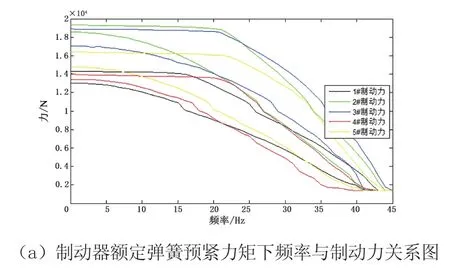

图5 频率与静态制动力关系
3 基于实验数据的可靠度求解
根据《起重机设计手册》[9]可得,圆盘式制动器的制动力为

式中:Mb为额定制动力矩,d1为有效摩擦直径,z为动摩擦制动盘数。
正压力为

式中:μ为摩擦系数。
根据应力强度干涉理论,建立如下离散功能函数

式中:N(f=0 )为常规制动器正压力,Nf为实验获取的随频率变化的正压力均值,n为智能制动器与常规制动器制动时间比。
式(6)体现了智能制动策略,即延长制动时间,实现抱而不死,缓慢耗能,减少冲击;同时制动时应满足制动力足够大,保证制动功能。
在处理实验数据后,获得了各频率下的静态制动力分布规律,按此分布规律,采用蒙特卡洛抽样法或一次二阶矩法根据离散功能函数计算各个离散点的可靠度及失效概率。计算过程中,涉及到的制动器本身参数及其分布规律如表1所示。
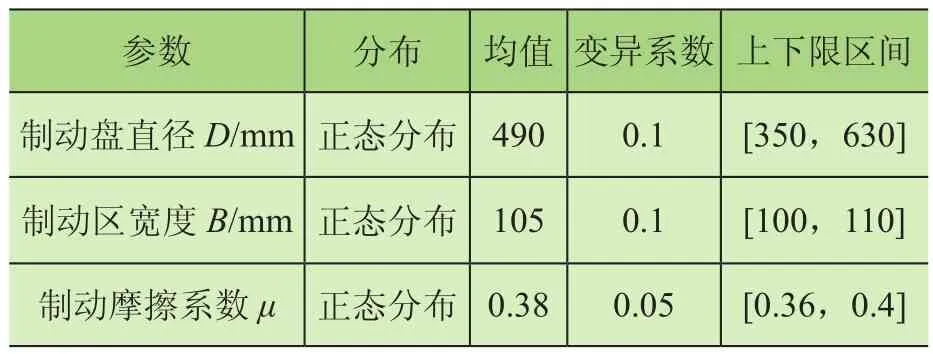
表1 制动器参数
取n=1~4情况下的可靠度数据并绘制成可靠度曲线,如图6所示。

图6 频率-可靠度曲线图
获得离散失效概率后,采用最小二乘法或者多项式拟合对失效概率与频率进行回归分析,获得失效概率与频率的关系为

4 基于目标SIL等级的频率区间划分
4.1 SIL划分
IEC61508《电气/电子/可编程电子 安全系统的功能安全》提供的划分准则如表2所示。

表2 SIL划分标准
4.2 频率区间的数学模型的求解方法
根据起重机工作级别,规定目标SIL等级,根据表2得失效概率的上下限分别为PL、PU。
通常制动力越大,制动效果越好,但当制动力过大容易导致在制动盘制动时表面摩擦过大,也不易实现平缓制动效果。为了综合性能和成本需求,引入SIL作为约束,一方面可以保证制动器的失效概率控制在设计要求范围内,另一方面保证了制动的可靠性。根据上述分析,可建立如下优化数学模型

式中:SILcal为计算得到SIL,SILobj为根据起重机工作级别得到的目标SIL。
当保证制动力尽可能大时,即保证可靠性尽可能大,根据表2,上述模型可进一步转化为

式中:PL和PU为SILobj对应的失效概率上下限。
由式(9)可获得频率—可靠性曲线,根据各目标SIL等级优选对应的频率范围,表3即为SIL等级1~4情况下的优选频率范围。

表3 SIL各等级优选频率范围
图7为n=2情况下的对应频率-可靠性曲线。
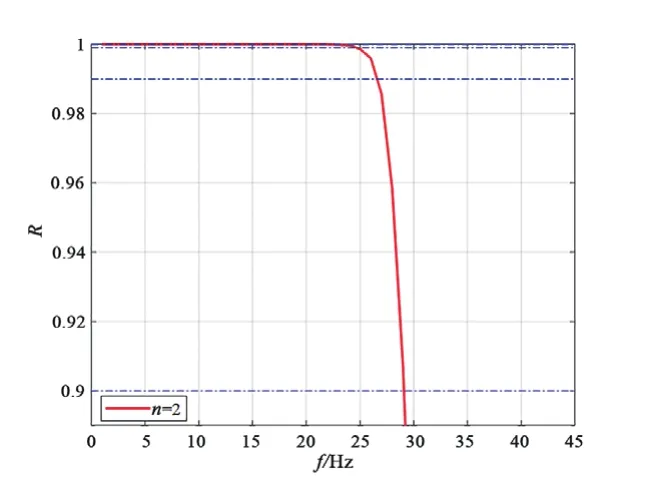
图7 频率-可靠性曲线图
5 结论
智能制动器采用智能制动策略,通过控制制动频率控制制动力的大小,在有效制动的前提下避免了制动冲击。本文通过实验采集制动全过程数据,建立数学模型,并基于SIL等级,建立优化出了最优的制动器工作频率区间。通过优化结果,可见SIL等级越高,制动频率区间越窄,其整体偏向低频区间。
