基于曲波域自适应导向滤波的海上采集脚印压制方法

陈 平,秦 童,郭 军,李少轩

(中海石油(中国)有限公司天津分公司,天津300459)

在海上和陆上地震勘探中广泛存在采集脚印,给地震构造勘探和储层地球物理研究带来较大影响。海上拖缆的地震采集脚印与地震采集方向有高度的耦合性,其主要特点是沿着采集方向或某一个特定角度,浅层切片或方差数据体上出现周期性的振幅假象[1-2],浅层表现比深层表现更为明显,有些会造成相位的移动,有些会造成时差的错动,在剖面上可见类似垂直断层的假象。采集脚印的存在对复杂断裂活动区的断层解释带来严重的干扰,当采集脚印影响范围涉及到目的层时,会对砂体的尖灭点识别以及连通性判断产生影响。采集脚印会直接影响勘探井位部署和开发方案设计,使海上油气勘探的高效评价面临较大挑战。

采集脚印的压制或消除方法分为3类[3]。第1类是优化采集设计的方法。王彦仓等[4]、碗学俭等[5]、骆宗强等[6]认为陆上采集脚印主要与观测系统的滚动方式、炮线距和接收线距相关,减小滚动线数、增大横纵比等可压制采集脚印的影响;谢玉洪等[1]、王征等[2]、张旭东等[7]认为海上采集脚印还受非观测系统影响,包括潮汐、水温、含盐度、水流方向等,采集时精确记录上述参数有利于后续处理工作。第2类是改进叠前处理方法,如针对海上拖缆羽漂、转圈造成采样不规则的面元中心化技术,针对残余时差的剩余静校正技术[1],减小线距的OVT域内插法[8]和振幅均衡后的加权叠前偏移处理技术[9]。这两类方法虽然能够从照明、覆盖次数和空间一致性的角度解决采集脚印问题,但耗时费力。第3类是进行叠后压制的方法。此类方法较多,发展也较快,如CHOPRA等[10]提出的f-k域滤波法,GÜLÜNAY[11]提出的Kx-Ky滤波法,邹振等[12]在其基础上提出的拉普拉斯Kx-Ky滤波法,陈学华等[13]提出的一种基于自适应三维平稳小波变换的方法,蔡涵鹏等[14]提出的一种完备经验模态分解的方法。此外,还发展出一些基于图像处理的方法,如AL-BANNAGI等[15]提出的奇异值分解方法、魏天罡等[16]提出的Garbor滤波方法。这些叠后处理方法存在一定的适用性或局限性:f-k域滤波由于自身假频和与有效信号叠置问题,或使断层模糊、主要地震反射特征发生变化;同时由于海上拖缆周期性差,波数域滤波效果有时并不理想。而主成分分解或Garbor滤波会极大改变资料本身,只能用于解释性处理;小波变换和经验模态分解的基函数是各向同性的,分解的维度不足以紧致表征包含采集脚印及断裂发育的复杂地震纹理结构,导致去除采集脚印后断面、断点等有效地震纹理受影响。

针对上述问题,本文提出基于曲波域自适应导向滤波的海上采集脚印压制方法。利用曲波变换独特的“似针状”基函数和各向异性分解优势,最优稀疏表征复杂的地震纹理,在海上地震资料全部时空范围内,采集脚印被视为一种不规则噪声,以地震优势方向为导向,能在高维的曲波域与地震信号较好区分并得到压制。

1 方法原理

小波变换类地震去噪方法是先对地震数据进行稀疏分解,即寻找到一个合适的稀疏变换基,在变换域中用较少的系数表示原始数据的主要特征,然后利用不同稀疏分解方法对细节刻画的特点,设计相关阈值以消除特定类型的噪声,达到提高信噪比的目的[17-18]。小波变换的基函数是各向同性的,以“点”为单位捕捉图像特征,无法紧致表达存在复杂纹理结构的地震数据,而曲波变换具有很强的方向敏感性和获取平滑轮廓的能力,在去噪效果和相对原始数据的保真度上有优势[19-20]。曲波变换于20世纪90年代首次提出,第一代曲波变换又叫块Ridgelet变换,但由于脊波基几何形态不清晰,有时对具有奇异性的直线逼近效果不佳,随后很快提出了第二代曲波基,其冗余度更小,且易于理解和实现,本文基于第二代曲波变换进行采集脚印的压制。

信号在连续曲波域进行稀疏分解可写成:

c(j,l,k)=〈f,φj,l,k〉

(1)

式中:c(j,l,k)为曲波系数;j,l,k分别为曲波函数的尺度、方向和位置参数;f为期望分解的信号;φj,l,k表示时空域的曲波函数。在频率域实现曲波变换更为高效,用频率域窗函数Uj代替φj,l,k,在频率域极坐标(r,θ)下,定义频率窗Uj为:

(2)

式中:[j/2]为j/2的整数部分;Uj为极坐标下的一个楔形区域,是一个个同心的圆环,符合各向异性的尺度特性,数值上正比于半径窗W(r)和角窗V(θ)的乘积。依据这两个窗函数可以对频率域进行多尺度、多方向划分,求同一尺度任意方向、位置上的φj,l,k可先将Uj(ω)反变换到时间域,然后对φj旋转和平移。定义旋转角度序列θl和平移参数k:

θl=2π·2[-j/2]·l,l=0,1,…,且0≤θl≤2π

(3a)

k=(k1,k2)∈Z2

(3b)

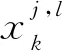
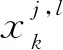
(4)

其中,Rθl表示旋转θl弧度。则(1)式可写为:

(5)

式中:f(x)为时空域信号。将时空域的内积转换到频率域,(5)式进一步写成:

(6)

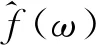
(7)

其中,Vj(Sθlω)是频率域角窗,Sθl是一个剪切矩阵。离散曲波变换使用同心矩形环状区域替代连续曲波变换中的环形区域,实现尺度和角度的划分。在空间域,单个楔形窗对应的曲波基为“似针状”的,在三维时空域垂直于脊的方向,单个楔形窗对应的曲波基是震荡的,而平行于脊的方向是低通平滑的,因而能更好地描述地震纹理结构以及边缘信息。

海上由非观测系统导致的采集脚印与水流、风向、潮汐等相关,这些因素在全部采集时空范围内可认为是随机的,与拖缆方向一致的有限时空则为较强的相干噪声,即采集脚印。假设垂直采集方向即联络线方向能看作连续时空的二维切片,采集脚印则近似等效为随机噪声,表现为时差错动或相位变化,与垂直断层尤为类似,一定程度上可认为是波形的“奇异点”。曲波变换的楔形基具有很强的非线性逼近能力,这些“奇异点”被分解到曲波域各个尺度、方向和位置上,与地震纹理的曲波域映射相比,其系数方向和能量更为发散,而地震有效信号则相对集中,因而在曲波域具备区分和压制采集脚印的条件。

曲波按照分解的尺度可分为内层、中间层和最外层,越靠近内层频率越低。内层用来表征信号的概貌,外层表征信号的细节和边缘特性。除了前面描述的区别,采集脚印相对于地震的曲波系数还存在内层系数小、外层系数大,近垂直方向系数大、近水平方向系数小的特点。这要求压制过程中曲波系数的阈值随分解尺度(或层数)和方向同时变化,这样才能在保留断层及同相轴等有效信息的前提下压制采集脚印。设计自适应阈值函数td为:

(8)

(9)

式中:cel为取整运算符,意为向上取整;len(C{s})为返回曲波系数C{s}在s尺度下分解方向个数;σ反映阈值整体的高低;α,β是经验参数,反映尺度和方向对阈值影响的程度。(8)式中绝对值项用于返回逻辑值,控制优势分解方向,默认为垂直和近垂直方向。由于曲波域1、3象限,2、4象限是中心对称的,(9)式中用顺时针180°区间变化的角度参数w0代替360°区间变化的角度参数w。

自适应阈值函数会随分解尺度和分解方向变化而变化,即在同一尺度下,阈值会随分解方向减小,而在同一方向上,阈值会随尺度(或层数)增加而增加,同时增加优势分解方向为约束条件,以满足采集脚印压制要求。在实际应用中,σ可先近似等于噪声能级水平的1/10,固定σ依次测试参数α,β,为保证采集脚印的压制效果,并有效保护较为复杂的断层纹理,分解尺度s的指数权重α应小于2,分解方向w0的指数权重应不大于1。

将上面得到的阈值应用于归一化后单位矩阵的曲波域系数E{s}{w0},有:

(10)

式中:L2为欧式范数运算符;nel为求矩阵元素个数运算符;C0{s}{w0}是单位矩阵的曲波域系数。采用硬阈值滤波,进而得到压制后的曲波系数Ct{s}{w}:

Ct{s}{w}=C{s}{w}·(|C{s}{w}|≥td·
E{s}{w})

(11)

对压制后的曲波系数进行反变换,便得到压制采集脚印后的联络线地震剖面,对所有联络线重复上述操作,就能得到压制采集脚印后的三维地震数据体。

2 模型试算

首先考虑单一水平界面的地震道模型,地震道数为500道,地震记录长度为1000ms,采样率为2ms,在500ms处设置反射界面,应用主频为35Hz雷克子波进行褶积,并在第150道和第350道添加近似等效采集脚印的2～5个样点时差。图1为单一水平界面地震道模型去除采集脚印前、后的对比结果。

采用离散曲波变换进行分解,分解尺度为5。图2 是去除采集脚印前、后地震道模型第1层至第4层曲波系数矩阵构成的图像,逐层进行了归一化处理。图像内层表示大尺度分解的曲波系数,其中最内层是各向同性小波分解后的结果,图像外层表示小尺度分解的曲波系数,各层都有4条边,分别顺时针存放3π/4至π/4,π/4至-π/4,-π/4至-3π/4,-3π/4至3π/4四个方向区间分解后的曲波系数。含采集脚印的地震道模型在非优势方向出现许多微小的曲波系数,尺度越小或越靠近外层,曲波系数值越大,如图2a 所示。直接滤除非优势方向的全部曲波系数(图2b),再反变换回时空域,采集脚印得到较为明显的压制,说明通过各向异性曲波稀疏分解,能够较好分离和表征采集脚印与有效信号(图1b)。

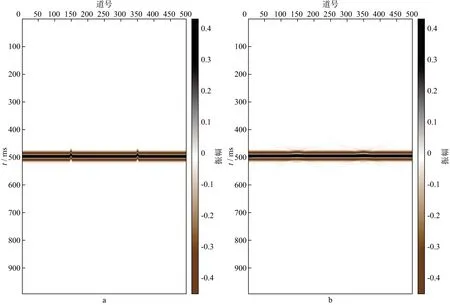
图1 单一水平界面地震道模型去除采集脚印前(a)、后(b)的对比

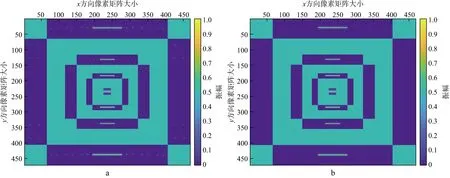
图2 单一水平界面地震道模型去除采集脚印前(a)、后(b)曲波系数对比

实际地层产状是变化的,且构造更为复杂,设计接近实际地下反射结构的二维模型,如图3a所示,水平方向为13000m,垂直方向为4000m,模型存在一条长期活动的边界断层及两条伴生断层,断距随断层的规模和深度变化。用主频30Hz子波正演得到二维模型的合成地震剖面,如图3b所示。并给复杂模型的正演地震记录添加部分采集脚印,如图3c所示,可以看到明显的同相轴抖动,容易解释为“垂直断层”。

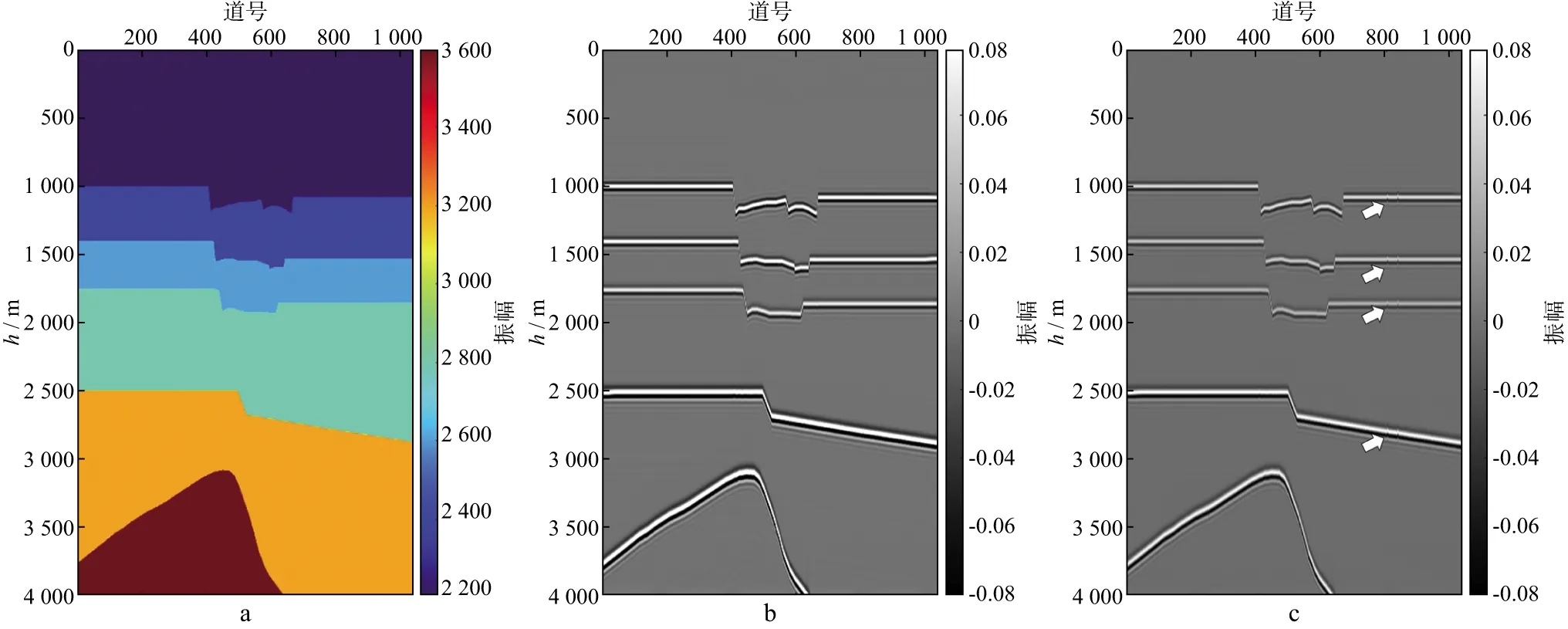
图3 复杂模型(a)、地震正演剖面(b)及含采集脚印地震剖面(c)

采用曲波变换对其进行5层分解,图4是1～5层曲波域系数矩阵组成的图像,可见主要地震能量集中于近垂直方向上,但其它分解方向除包含采集脚印外,也包含断层等其它纹理信息(图4a),因而不能直接滤除曲波系数。应用本文方法进行压制后,有效信号的曲波域系数得到较好保留(图4b),将压制前、后的曲波系数矩阵直接相减,能看到系数差值在不同尺度和方向上是变化的(图4c),且近垂直方向和与断面有关的分解方向上系数差值较小,说明本文方法较为合理。

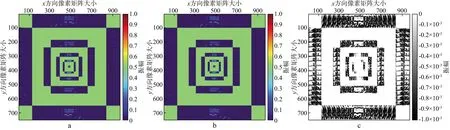
图4 复杂模型正演地震记录曲波域系数对比a 去除采集脚印前; b 去除采集脚印后; c 系数相减结果

图5是压制采集脚印前、后复杂模型地震剖面,压制采集脚印后主要的地震反射特征基本不受影响,同相轴产状变化自然,断层及断裂组合无明显异常,采集脚印得到较好的压制,资料品质得到改善。

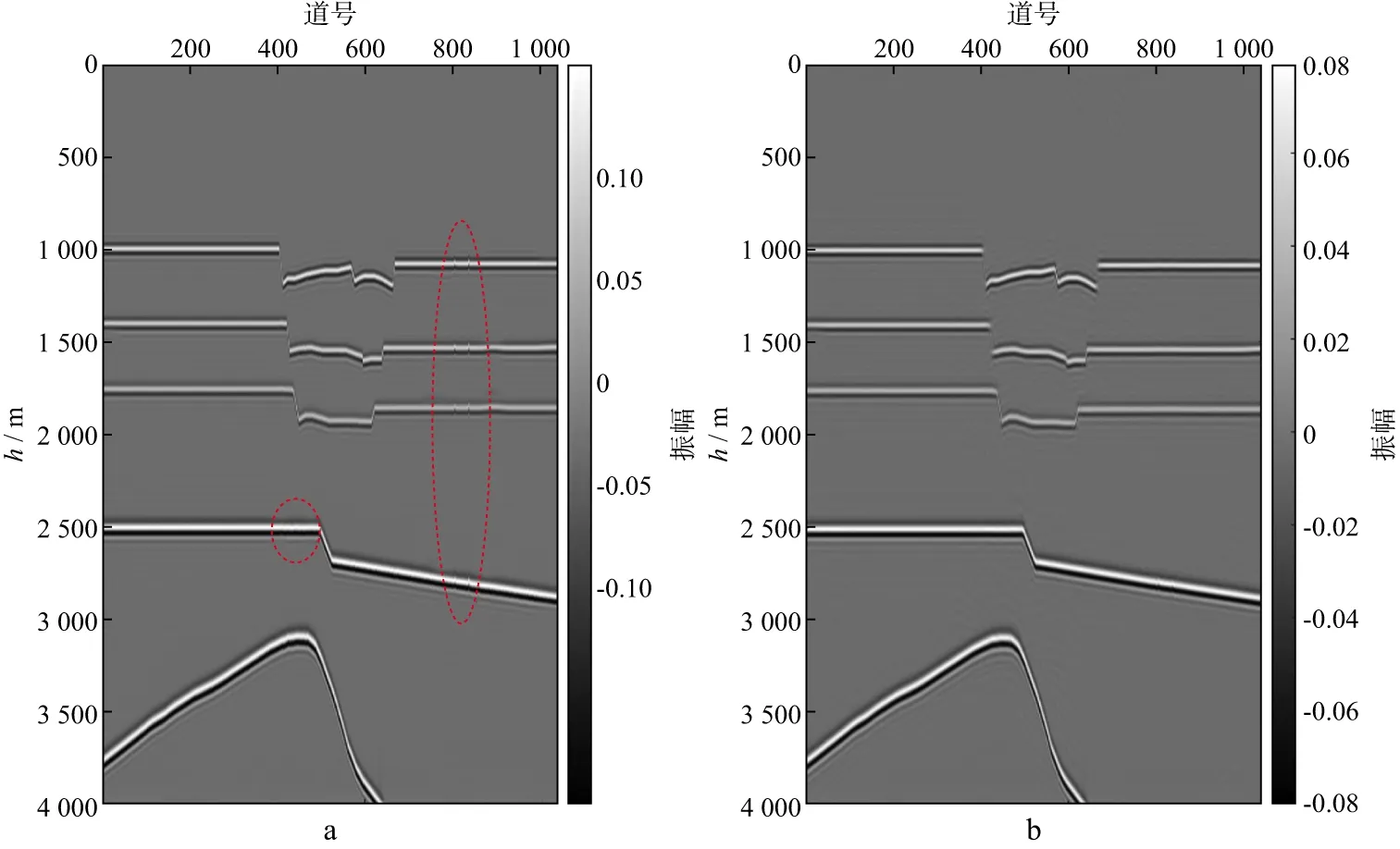
图5 压制采集脚印前(a)、后(b)复杂模型的地震剖面

3 实际应用

曹妃甸某油田位于渤中凹陷西斜坡的构造脊上,断层活动性强,有利于浅层油气的运移和汇聚。油田及围区发育北东东向和近东西向的断层,断层配置关系复杂,和浅层砂体互相耦合,形成一系列有利的构造-岩性圈闭。该区海上拖缆地震资料沿北偏西45°采集,拖缆作业时间近8个月,受冬季季风、渔业活动和潮汐等多种因素影响,加上处理时间较早,地震资料的采集脚印较为发育。图6为曹妃甸某油田去除采集脚印前、后方差数据体切片,可见500ms、1000ms原始方差数据体切片均存在北—西向、与拖缆采集方向相关的采集脚印,1000ms方差数据体切片断层“毛刺”现象较为明显(图6a、图6c)。采集脚印的存在直接影响浅层断裂系统的组合,也影响新近系浅水三角洲储层的精细刻画。

图6 曹妃甸某油田去除采集脚印前、后的方差数据体切片a 500ms原始方差数据体切片; b 500ms去除采集脚印后方差数据体切片; c 1000ms原始方差数据体切片; d 1000ms去除采集脚印后方差数据体切片

采用本文方法进行采集脚印压制,经过测试和实验可知,当σ=0.004,α=1.6,β=0.5时,阈值函数能较好压制本区采集脚印。如图6b、图6d所示,500ms方差数据体切片上消除了大部分采集脚印导致的异常相干能量,1000ms方差数据体切片上断层“毛刺”现象得到一定减弱,断裂特征更为明确,有利于厘清断层的平面组合关系。

图7是去除采集脚印前、后联络线地震剖面,可以看出,原始剖面上采集脚印从250ms延伸到950ms,浅层由于频率较高,波组错断更为明显,容易误判为“垂直断层”(图7a),处理后在一定程度上消除了这种“垂直断层”的解释误区,地震波组特征更为自然(图7b),在差剖面中能看到压制的采集脚印,且有效信号基本不受影响(图7c)。

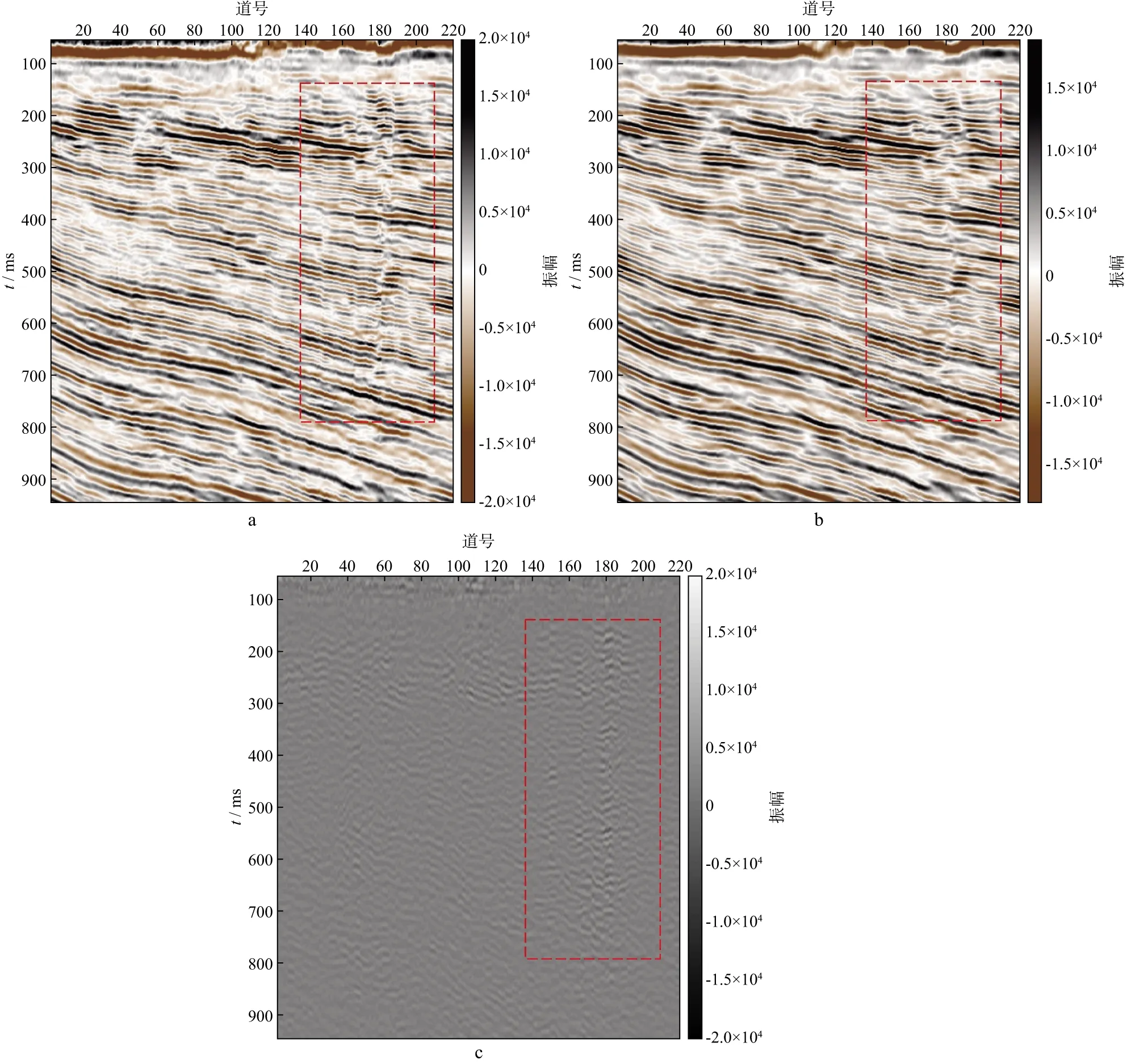
图7 去除采集脚印前、后联络线地震剖面a 去除采集脚印前; b 去除采集脚印后; c 差剖面

基于新资料对全区已追踪砂体重新排查后发现,部分砂体的尖灭位置和连通关系发生变化。图8给出了去除采集脚印前、后潜力砂体的对比结果,可以看出,原始地震剖面上,975砂体高部位基本尖灭在采集脚印处的位置(图8a),处理后的地震剖面上,975砂体往高部位还是连通的(图8b),差剖面中对应位置的能量也较为集中在采集脚印附近(图8c)。

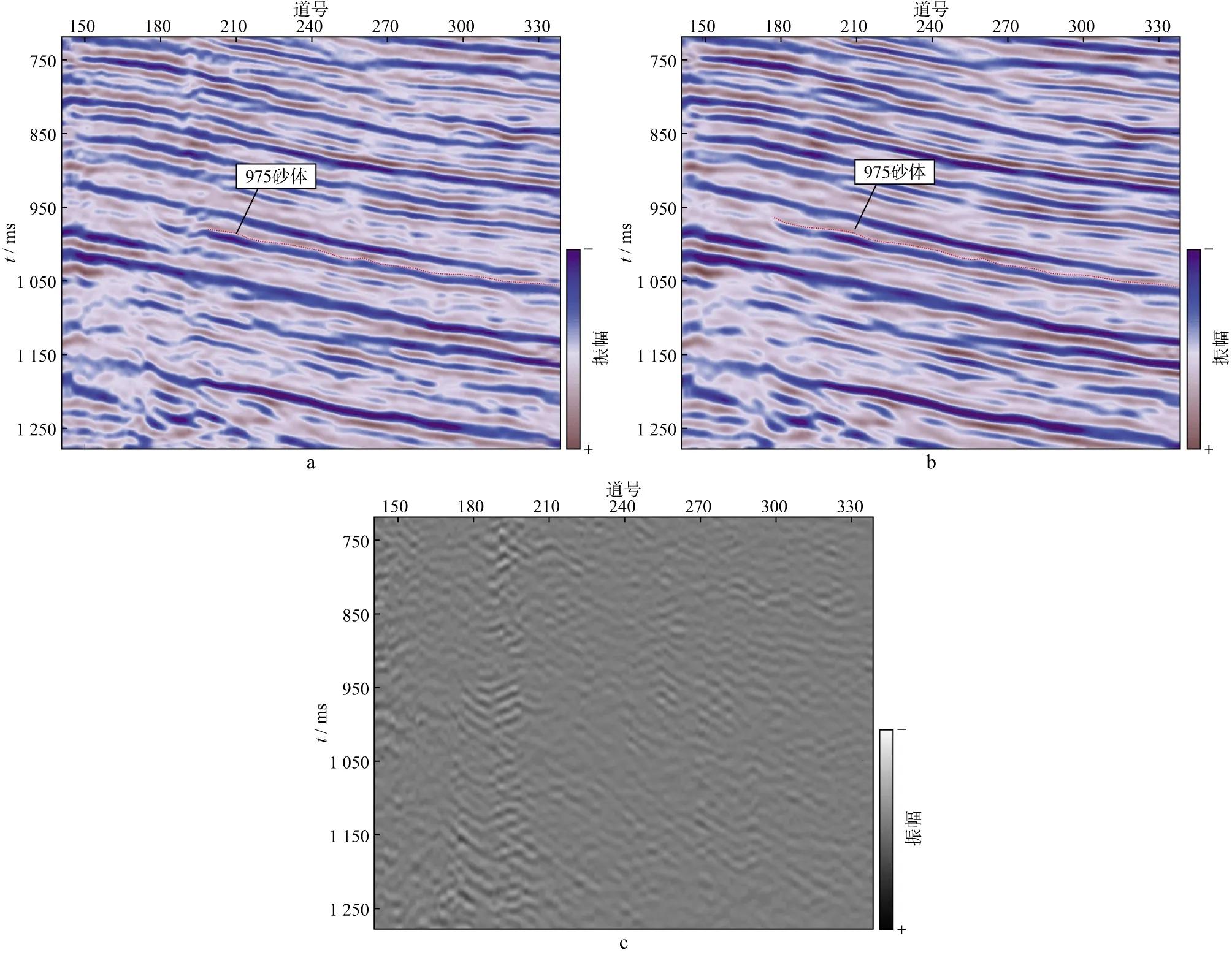
图8 去除采集脚印前、后潜力砂体的对比a 去除采集脚印前; b 去除采集脚印后; c 差剖面

综合分析认为,该区采集脚印的存在不仅影响地震资料解释结果,也影响构造-岩性控制下储层的精细描述,对油田周边挖潜有较大影响,采用有效的采集脚印压制技术十分必要。

4 结论和建议

海上采集脚印由于周期性差和与断面类似的纹理,常规方法无法有效压制或改善原始地震资料品质。本文提出在垂直于采集方向可近似将采集脚印看作连续时空内的“奇异点”,利用曲波变换各向异性和地震纹理表达的优势,将其映射到相比小波变换更高维度进行区分和压制,并给出针对复杂地质构造的自适应导向滤波方法。模型和实际应用结果均证明了方法的有效性和适用性,能消除浅层大部分采集脚印造成的地质解释假象。

本文方法除用于压制采集脚印外,也可作为一种保边缘提高信噪比的一般方法。实际应用中经验参数对采集脚印压制效果较为敏感,需按照一定顺序不断测试。另外,本文采用硬阈值的方法进行滤波,采用软阈值滤波方法能进一步减少反变换后的“吉布斯”现象。