基于污染气体释放特征的排污效率计算方法与工程应用*

2021-12-02上海理工大学张倩茹同济大学

暖通空调 2021年11期

关键词：易燃易爆排风测点

上海理工大学张倩茹同济大学张旭叶蔚高军

0 引言

(1)

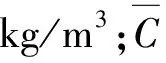
当送风中不含污染物时，式(1)可以简化为

(2)

在研究室内环境时，通常假设示踪气体为被动气体，从而排污效率只与气流组织有关。凌继红等人通过实验研究了气流组织对负压隔离病房排污效率的影响，在病人口部散发SF6示踪气体，通过测量医护人员呼吸区域的污染物浓度，比较了8种气流组织的排污效率[5]。杨建忠等人以B737-200客机座舱模型为研究对象，用排污效率评价了天花板送风、侧壁送风、混合送风的效果[6]。王怡等人针对具有集中热源和集中污染源的工业厂房，研究了复合通风系统室内竖直温度分布、温度效率和排污效率的变化规律[7]。杨鹏等人研究了不同送、排风形式对脱水机房的排污效率和恶臭浓度的影响规律[8]。郑晓红等人针对医院病房内易出现病人间通过空气途径发生传染病交叉感染的问题，提出一种发散源可控的局部空调个性化通风装置作为空调系统末端，并用排污效率评估了传统空调和该个性化通风系统的性能[9]。吴小舟等人利用办公房间室内热环境参数分布及新风系统的通风效率对低温辐射地板供暖系统分别与混合通风系统和置换通风系统复合的效果进行了评价[10]。李安桂等人根据排污效率对新型冠状病毒肺炎医院的典型隔离病房进行了气流组织的有效性评价[11]。

当污染物释放量较大或者污染物密度与空气密度相差较大时，污染气体的初始释放特征会影响其附近的流场，从而影响污染物在室内的分布[12]。赵鸿佐针对非等温房间，得到通风(温度)效率ET与阿基米德数(Ar)的对数之间存在线性关系的结论[13]。而房间的热、质传递具有相似性[14]，因此在机械通风背景下，排污效率则应与表征机械通风效果的量纲一数之间存在一定的关系。

本文通过理论分析推导得到有非被动污染气体房间的排污效率计算方式，用经过实验验证的数值模型进行一系列工况计算，并用数值模拟结果分析得到排污效率的表达式。

1 理论分析

Ar为浮力效应相似特征数，其物理意义为浮力与惯性力之比，对于密度比空气大的污染气体，Ar应表示为

(3)

式中g为自由落体加速度，m/s2；l为特征长度，m；Δρ为污染气体与空气的密度差，kg/m3；v为特征速度，m/s；ρa为空气的密度，kg/m3；ρg为污染气体的密度，kg/m3。

如果考虑从释放源离开后气体受到掺混，其密度应是掺混后的混合密度，那么该密度差应为

Δρ=ρmix-ρa

(4)

式中ρmix为混合物的密度，kg/m3。

而混合物的密度应为

(5)

式中Vg为参与混合的污染物体积，m3；Va为参与混合的空气体积，m3；qV为污染气体的体积释放速率，m3/s；QV为房间的通风量，m3/s。

由于qV≪QV，所以

(6)

经过对混合物密度的修正，表征混合气体负浮力与惯性力之比的Ar′可以表示为

(7)

如果将特征速度定义为房间横截面的平均风速v，特征长度定义为房间横截面的特征长度l，那么QV=vl2，式(7)可以表示为

(8)

式(8)用污染源的释放量及相关参数对Ar进行修正，涵盖了影响室内气态污染物扩散的主要因素，定义气体扩散特征数Π=Ar′。当Π较小时，气态污染物的扩散主要受周围气流的惯性力作用；而当Π较大时，气态污染物的扩散主要受自身负浮力(或浮力)的作用。所以在量纲一数Π由小增大的过程中，起初污染物的扩散为被动气体扩散，随后逐渐向非被动气体扩散过渡。

在污染物缓慢持续泄漏时，稳态情况下室内污染物气体的分布状态决定了室内的排污效率。根据式(8)，影响气态污染物在室内分布的变量包括：特征风速v、特征长度l、污染气体释放量qV、空气密度ρa、污染气体密度ρg、自由落体加速度g。因此排污效率可以作为上述6个变量的因变量。

根据量纲分析法，可以得到6个变量中3个基本量的量纲一形式：

(9)

(10)

(11)

因变量排污效率本身即为量纲一参数，因此定义：

(12)

有如下关系：

Π4=f(Π1,Π2,Π3)

(13)

而根据笔者以往的研究，室内污染物的分布规律和表征气态污染物释放强度相对大小的量纲一数有关[12]，而量纲一数又可以表示为

(14)

因此式(14)可以变为

(15)

亦即排污效率与气体扩散特征数之间存在函数关系。式(15)的具体形式则需根据具体工况得到。

2 数值模拟验证

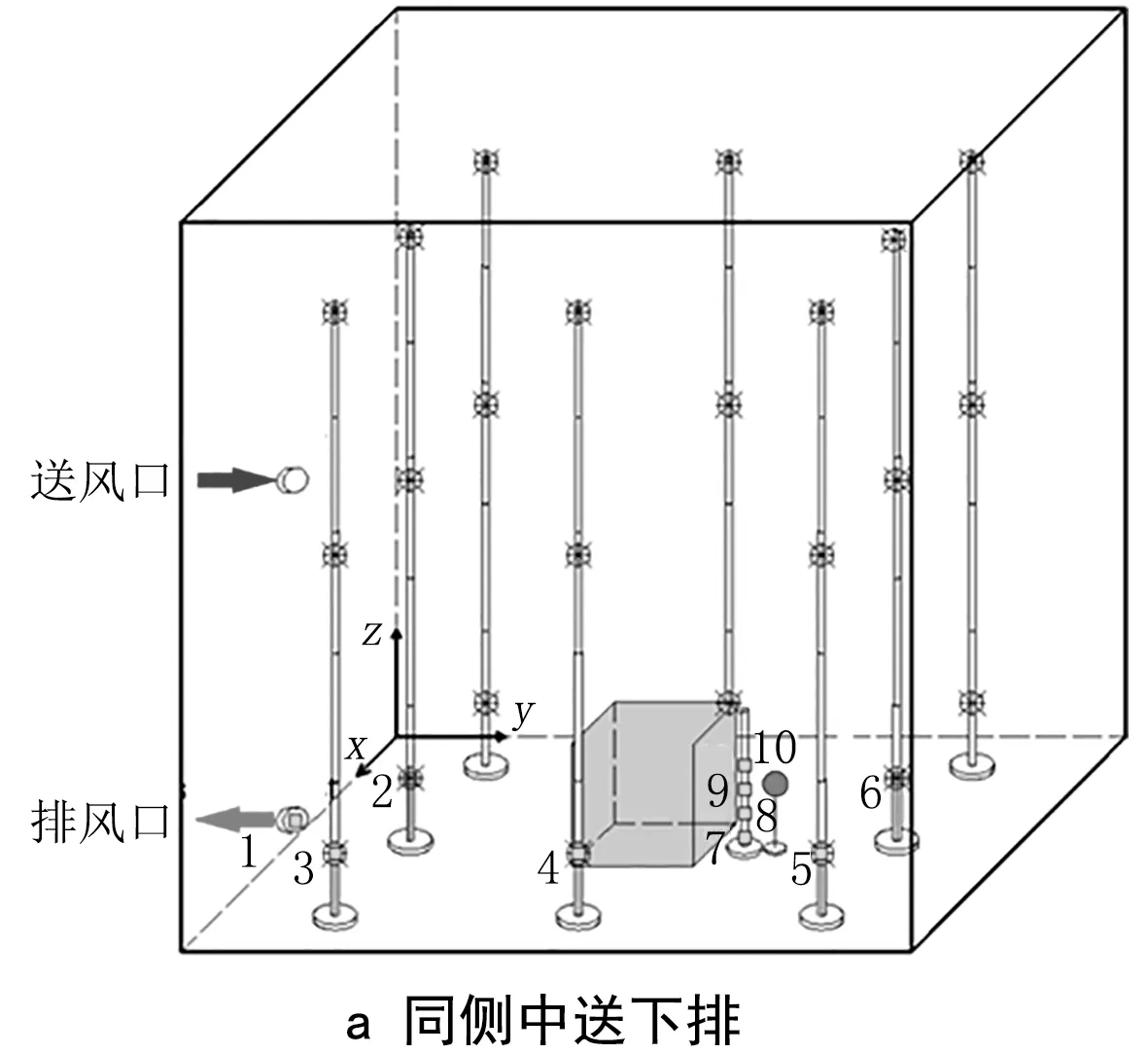
对数值模型进行验证的实验台为大空间污染物扩散及控制实验舱，如图1所示。本验证实验中的障碍物为由纸箱组合成1 m×1 m×1 m的立方体，放置在实验舱地面中心位置，实验中的污染源为布满小孔的乒乓球，如图2所示。

图1 大空间污染物扩散及控制实验舱

图2 障碍物及污染源示意图

实验中将污染源固定在障碍物一侧，并选取同侧中送下排和对侧中送下排2种气流组织情况进行研究。为了排除温度对污染物浓度分布的影响，选取等温的实验工况。将实验舱在各方向均匀划分为三部分，整个空间划分为27个子空间，温度测点和速度测点布置在各子空间的中心位置。由于排风口和污染源均在空间下部，因此浓度测点都设置在空间的下半区域。根据预实验的结果，除污染源附近浓度有明显差异，实验舱内其余位置浓度相对均匀，因此本实验中的浓度测点分为高浓度区域测点和低浓度区域测点。浓度测点1设置在排风口处，低浓度测点2～6设置在与污染源同一高度处。在障碍物与污染源之间离地0.1、0.3、0.5、0.7 m高处布置高浓度测点7～10，以得到污染源附近浓度在高度方向的变化。相应的实验测点布置如图3所示(当排风口设在对侧墙面时，排风口处的浓度测点亦随之变化)。

低浓度区域的测点1～6由特氟隆管连接到INNOVA光声光谱在线气体检测仪进行气体分析，而高浓度区域的测点7～10由泵吸式SF6检测仪进行测量。

2种工况的房间换气次数均为3 h-1，污染源的释放速率均为3.2 L/min，以验证在非被动扩散情况下数值模型的准确性。实验为稳态工况，气体释放约1 h后各测点浓度几乎不变，取此后一段时间的平均浓度数据来验证模拟结果。实验中各测点温度的变化不超过±1 ℃，因而认为工况为等温工况。实验中排风口下沿离地面的距离为0.14 m。

用standardK-ε模型、RNGK-ε模型和realizableK-ε模型对同侧中送下排工况的流场进行数值模拟，并将模拟结果与实验结果进行比较。图4显示了数值模拟与实验结果的对比。由图4可以看出：对比3种模型，RNGK-ε模型计算的射流轴心风速衰减最大，realizableK-ε模型衰减最小；对于射流运动路径上的2个测杆，standardK-ε模型计算得到的风速与实验值最为接近；对于非射流运动路径上的3个测杆，3种湍流模型的竖直速度分布曲线相似，并与5 m高的测点实验值接近，而在1 m和3 m高处，3种湍流模型的计算结果均高于实验值；综合各测杆处的对比结果，认为standardK-ε模型对流场的预测结果与实验值最为接近。因此选用standardK-ε模型进行后续计算。

图5给出了同侧中送下排和对侧中送下排2种工况下6个浓度测点的实验值和模拟值，图中量纲一浓度为各测点浓度与排风口处浓度的比值。

由图5可以看出，实验值和模拟值的分布趋势相似，测点9和测点10的浓度最高，说明在障碍物与污染源中间的区域受到气流的作用较大，污染气体密度产生的重力作用有限。经过验证的同侧中送下排和对侧中送下排模型将用于后续研究。

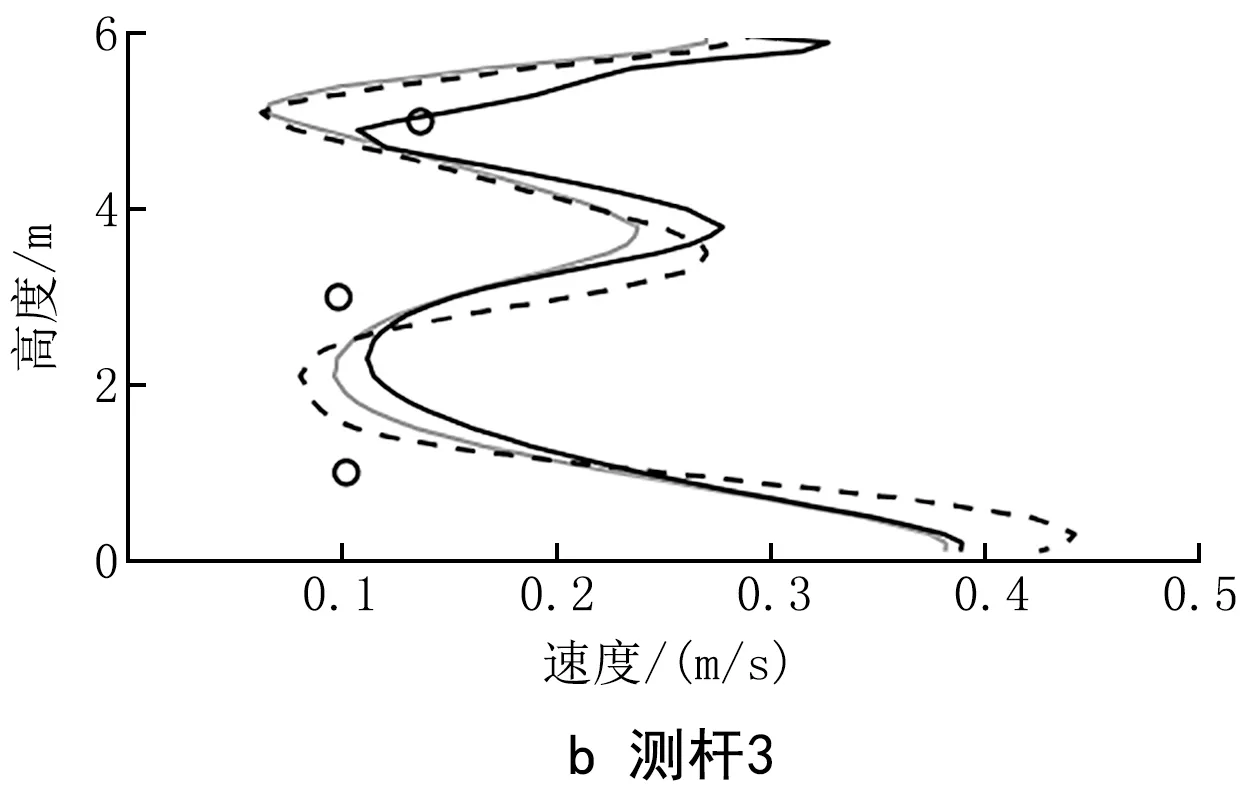
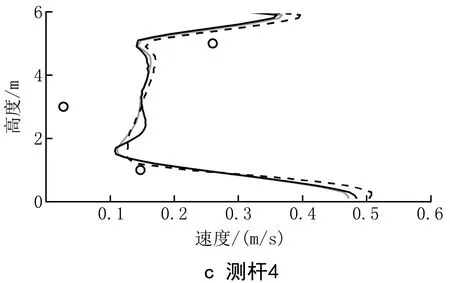
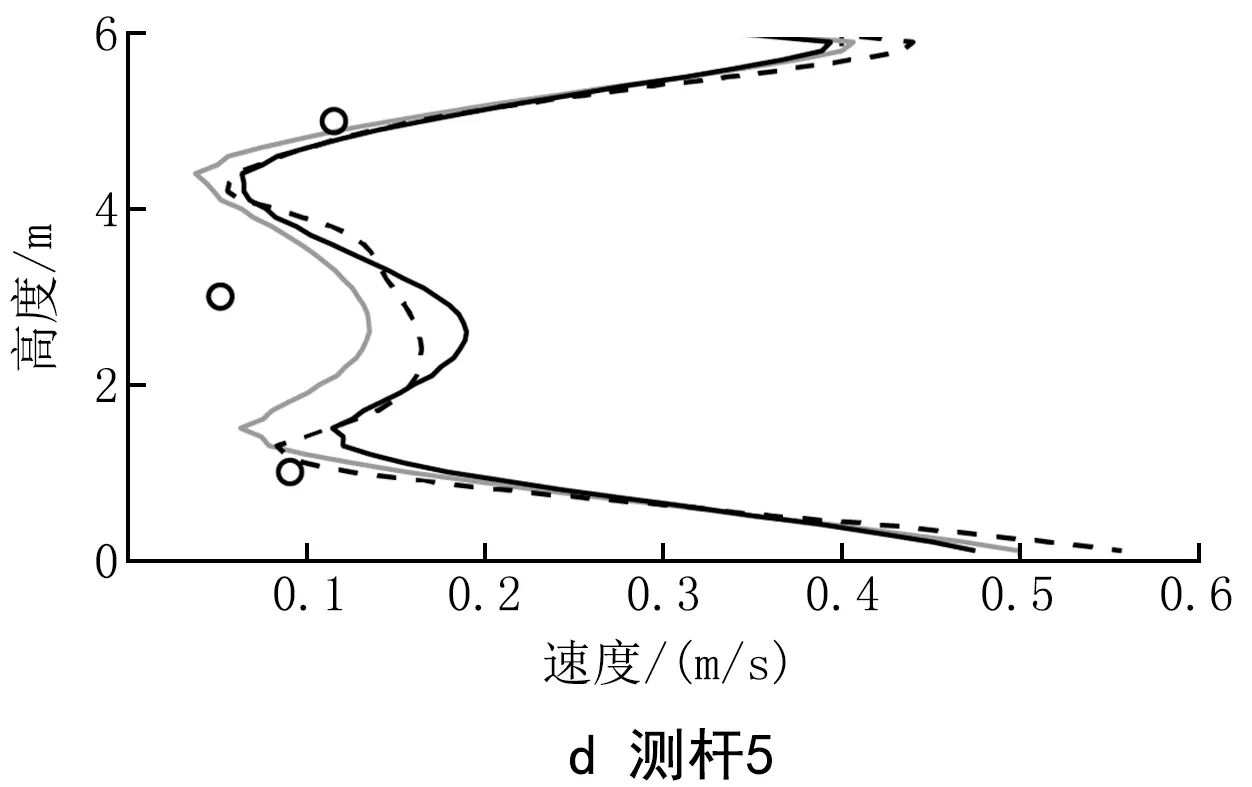
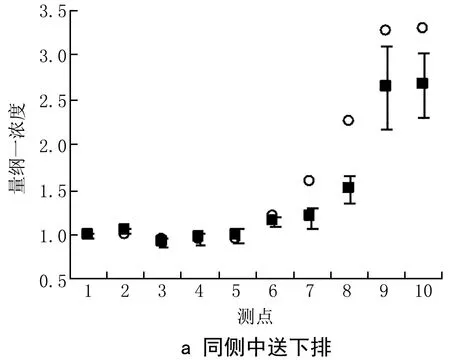
图5 浓度场模拟结果与实验值对比

3 工况设置

针对同一建筑和室内设计温度来探讨气体扩散特征数Π的大小，需要考虑气态污染物的密度、气态污染物的释放量和房间的特征风速三者的各种组合。

在各种实验设计方法中，三因素四水平的均匀设计可以用相对较少的工况数量综合考虑3个因素的影响[15]，并且便于拟合曲线，因此选择其作为研究几种因素综合作用的工况设计方法。

将因素1设定为污染物气体的质量流量qm。综合考虑以往研究中不同密度气体的泄漏量[16-22]，其数量级大部分分布在10-5、10-4、10-3kg/s。重型污染物缓慢持续泄漏工况选取1.60×10-5、4.80×10-4、1.28×10-3、1.60×10-3kg/s作为污染物气体缓慢持续泄漏量的4个水平。对于轻型污染物缓慢持续泄漏场景，由于其物理对象与网格都与重型污染物泄漏场景不同，这里将其换算成与重型污染物单位体积释放强度相同的量。

将因素2设定为污染物气体密度ρg。对于密度比空气大的污染物，选取C3H8、CH2F2、CCl2F2，并结合之前实验中用到的SF6，将其作为因素2的4个水平。

将因素3设定为房间的特征风速v，该风速取决于室内的换气次数。工业厂房一般要求换气次数不低于1 h-1，冷库相关的工业场合一般要求换气次数不低于3 h-1，因此选取1、2、3、4 h-1作为换气次数的4个水平，相应地可以得到对应建筑特征风速的4个水平。

在已经确定3个因素及其4个水平的情况下，可以得到均匀设计工况。重型污染物缓慢持续泄漏场景各工况相应参数及量纲一数如表1所示。

表1 重型污染物气体缓慢持续泄漏场景均匀设计工况及相应量纲一数

对于每组工况，都进行同侧中送下排和对侧中送下排的3种排风口高度的数值模拟计算。

4 结果与讨论

4.1 室内浓度与排污效率变化

图6为重型制冷剂缓慢持续泄漏采用同侧中送下排时8个工况对称面上制冷剂气体量纲一浓度C*的分布云图，按照各工况Π从小到大的顺序排列。其中量纲一浓度C*的计算式如下：

(16)

(17)

式(16)、(17)中C为当地污染物质量浓度，kg/m3；Ce为稳态排风中的平均污染物质量浓度，kg/m3；qm为污染物质量流量，kg/s。

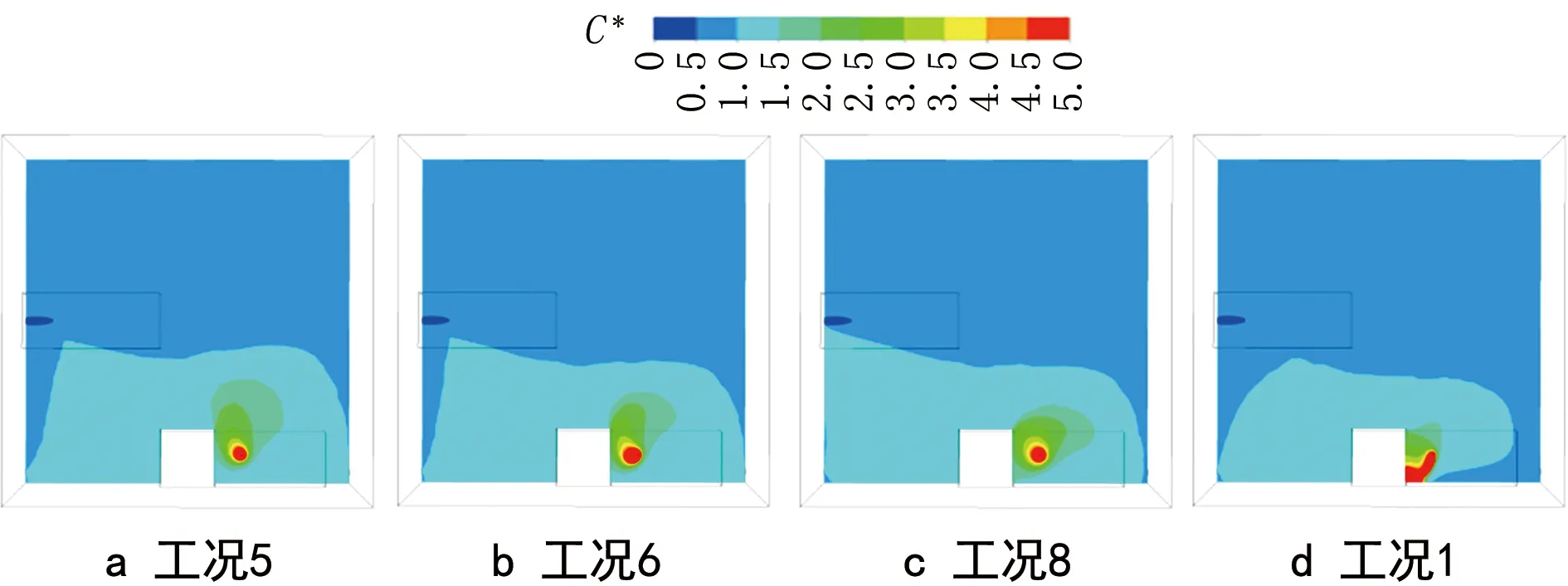
图6 同侧中送下排对称面上制冷剂气体量纲一浓度分布云图

由图6可以看出，随着Π的增大，污染物的扩散由被动气体扩散逐渐向非被动气体扩散过渡，室内量纲一浓度分布也逐渐转变为具有明显的竖直浓度分层，且随着高度增加，量纲一浓度减小。当Π≥50 168(工况2和工况4)时，污染源附近气流的惯性力相对较小，负浮力占主导地位，污染气体一经泄漏即形成了竖直下沉现象，整个截面上也形成由下至上的浓度分层。

4.2 排污效率计算公式

图7显示了同侧中送下排且排风口下沿距离地面140 mm时，按照表1设计的一组工况的排污效率与气体扩散特征数Π的变化关系。

图7 排污效率与特征数Π的变化关系

由图7可以看出，随着Π的增大，房间排污效率增大。结合前文Π和浓度分布之间的关系，由于排风口设置在侧墙底部，排风口处的污染物浓度较高，从而导致房间排污效率较高。并且随着Π的增大，排污效率起初增加较慢，后来增加较快，比较符合指数函数的形式，因此以指数函数拟合该数据关系。假设二者之间的函数关系式为

(18)

式中a1、b1、c1为实数。

对同侧中送下排、排风口高度为140 mm的工况进行曲线拟合，结果如图8所示。

图8 同侧中送下排、排风口高度为140 mm工况排污效率拟合曲线

图8中拟合曲线的表达式为

(19)

对拟合方程进行拟合优度检验，得到残差平方和为0.006 865，相关系数为0.998 6，均方根误差为0.037 05。拟合曲线的残差平方和与均方根误差都接近于0，而相关系数接近于1，说明拟合曲线对样本数据点的拟合程度很高。

考虑排风口在送风口同侧和对侧时，排风口下沿离地140、300、450 mm 3种排风口高度，共包括6种气流组织方案。图9显示了6种气流组织方案的排污效率与特征数Π的变化关系。

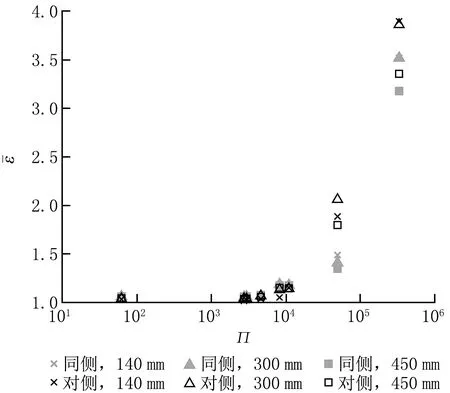
图9 各工况排污效率与特征数Π的变化关系

若考虑排风口高度对拟合公式的影响，引入排风口下沿距离地面的高度与特征长度相比得到的量纲一数Z/l(其中Z为排风口下沿距离地面的高度)，并假设排污效率的计算式为

(20)

式中a2、b2、c2、d为实数。

对同侧中送下排和对侧中送下排各工况数据进行拟合，其结果如图10、11所示。

图10 同侧中送下排工况排污效率函数拟合

图11 对侧中送下排工况排污效率函数拟合

图10、11中拟合曲面的表达式分别为

对拟合方程进行拟合优度检验，得到残差平方和为0.044 25，相关系数分别为0.996 8和0.978 1，说明拟合曲线对样本数据点的拟合程度很高。

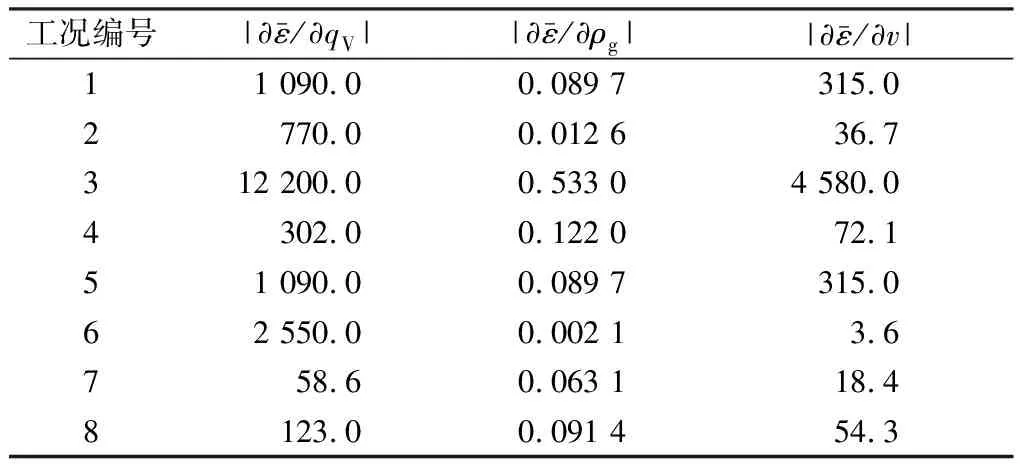
表2 排污效率对各变量的导数

4.3 排污效率计算方法的工程应用

一些室内污染气体有易燃易爆的可能性，因此室内通风需要同时考虑房间的排污效率和控制易燃易爆区域大小。

文献[23]中用实验方法研究了氦气在自然通风房间里的竖直浓度分布，得出了房间最大体积浓度和平均体积浓度都与体积释放强度呈线性关系的结论。这里对机械通风房间内超过一定体积浓度的区域也进行类似分析。将同侧和对侧工况3个排风口高度的易燃易爆区域体积比取平均值，体积比ζ随qV的变化如图12所示。

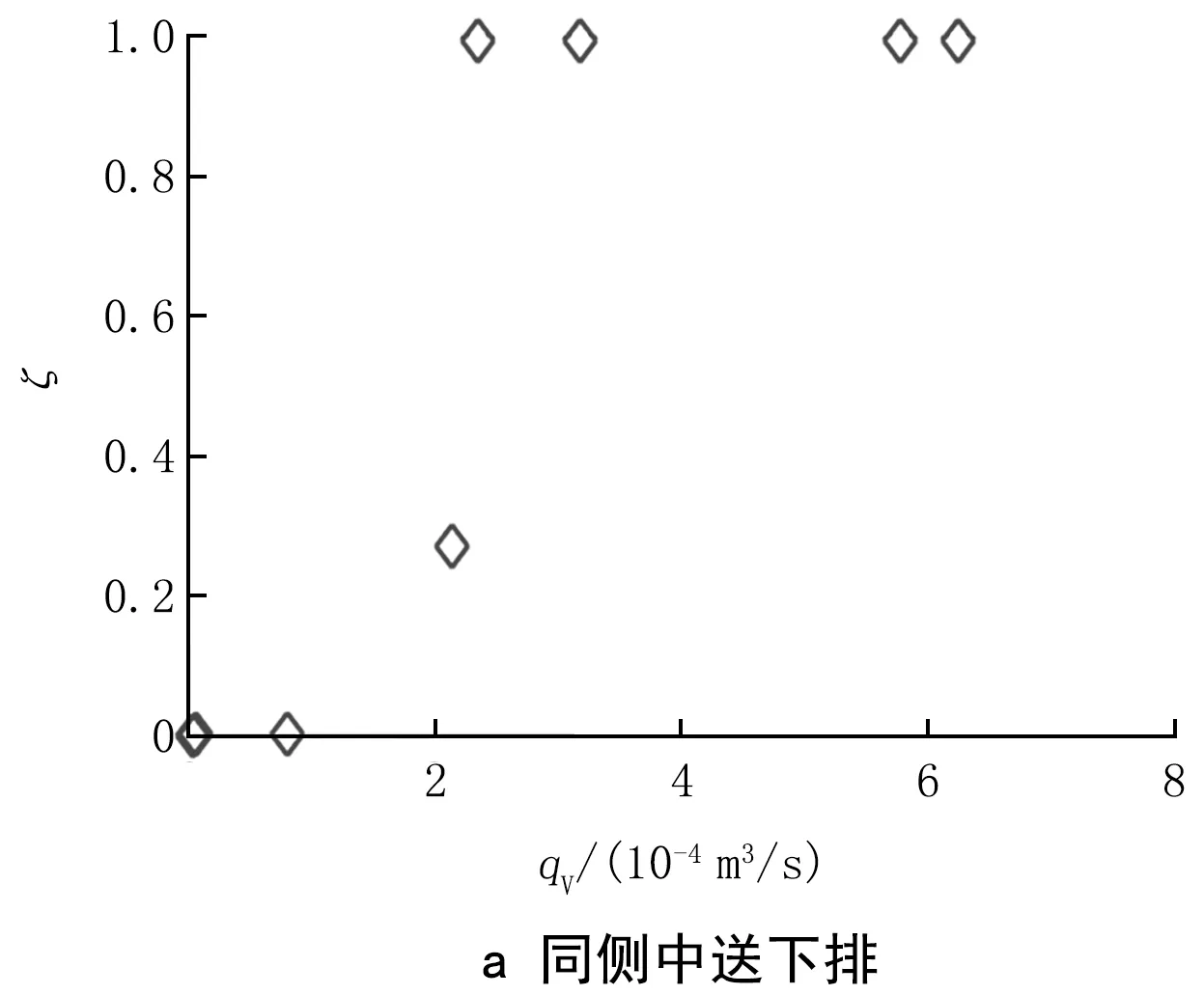
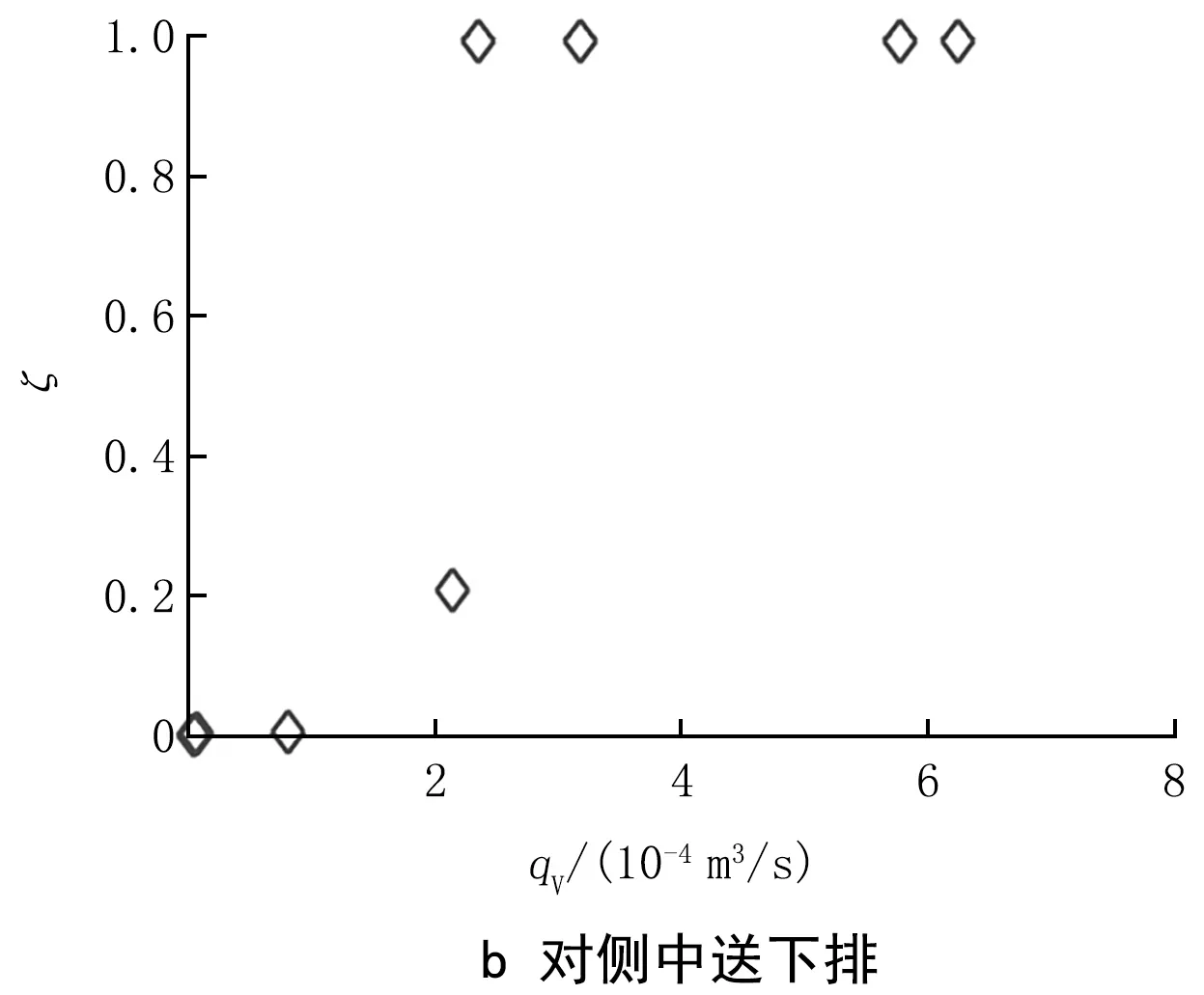
图12 易燃易爆区域体积比ζ随qV的变化

由图12可以看出，易燃易爆区域体积比随着体积释放速率的增大而增大，当释放速率小于8×10-5m3/s时，易燃易爆区域体积比为0，而当释放速率超过2.34×10-4m3/s时，易燃易爆区域的体积比为1。对于释放速率在8×10-5～2.34×10-4m3/s之间的工况，可以将其以指数函数拟合，房间易燃易爆区域体积比与体积释放速率之间的关系式为

(23)

采用线算图的方法将式(19)与式(23)所描述的排污效率与易燃易爆区域体积比的变化绘制出来，如图13所示。在不使用公式的情况下，可以利用图13，通过各参数查询得到房间整体的排污效率及易燃易爆区域体积比。图13可以同时评估排污效率与易燃易爆区域大小是否满足需求。

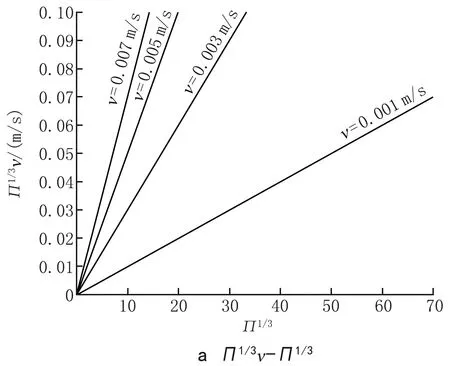
图13 同侧中送下排工况排污效率与易燃易爆区域体积比线算图

图13是在质量流量为1.6×10-5～1.6×10-3kg/s的点源、换气次数为1～4 h-1、污染物密度为1.83～6.04 kg/m3、排风口下沿距离地面0.1～0.4 m范围内得到的结果，因此适用于该参数范围内的中送下排的工业场合。当进行厂房通风气流组织设计时，可以根据厂房内污染物的种类、污染物潜在泄漏量、拟设计的通风换气次数、拟设计排风口高度查询相应的排污效率及易燃易爆区域体积比。对于有密度比空气大的污染气体微量泄漏的工业厂房，一般符合相应的参数范围，该线算图可以满足使用要求。