基于风机盘管机组换热特性的热力平衡分析
2021-12-02上海润风智能科技有限公司刘新民
上海润风智能科技有限公司 刘新民
0 引言
目前,业界有关集中式空调变流量冷水系统节能运行控制技术均以保障末端用户侧供冷服务质量为前提条件,但能够明确给出服务评价技术标准的文献和厂商却很少。
Robert原文采用的英文单词“hydronic”被译为“水力”[1]。于是,“hydronic balancing”被译成“水力平衡”,失去了原词“hydronic”中“热和冷”的含义。国内一些学者依据“水力平衡”的中文含义将其对应的英文改为“hydraulic balancing”,最终形成了将热量与水力割裂开来的学术认同[2-10]。
本文以设计工况下确保末端表冷器设计流量Qm为技术指标,以风机盘管机组(FCU)换热特性为例,试图从“hydronic”的视角对风机盘管机组换热特性的热力平衡进行分析与讨论。
1 FCU换热特性
2020年7月1日开始实施的GB/T 19232—2019《风机盘管机组》第3.5条对风机盘管机组额定供冷量(rated cooling capacity)的定义为机组在规定试验工况下的总供冷量,即显热量和潜热量之和[11]。文献[12]给出了FCU试验样机在GB/T 19232—2003《风机盘管机组》[13](以下简称GB/T 19232—2003)规定的标准试验工况下获得的变流量换热特性试验测试数据(见表1)。
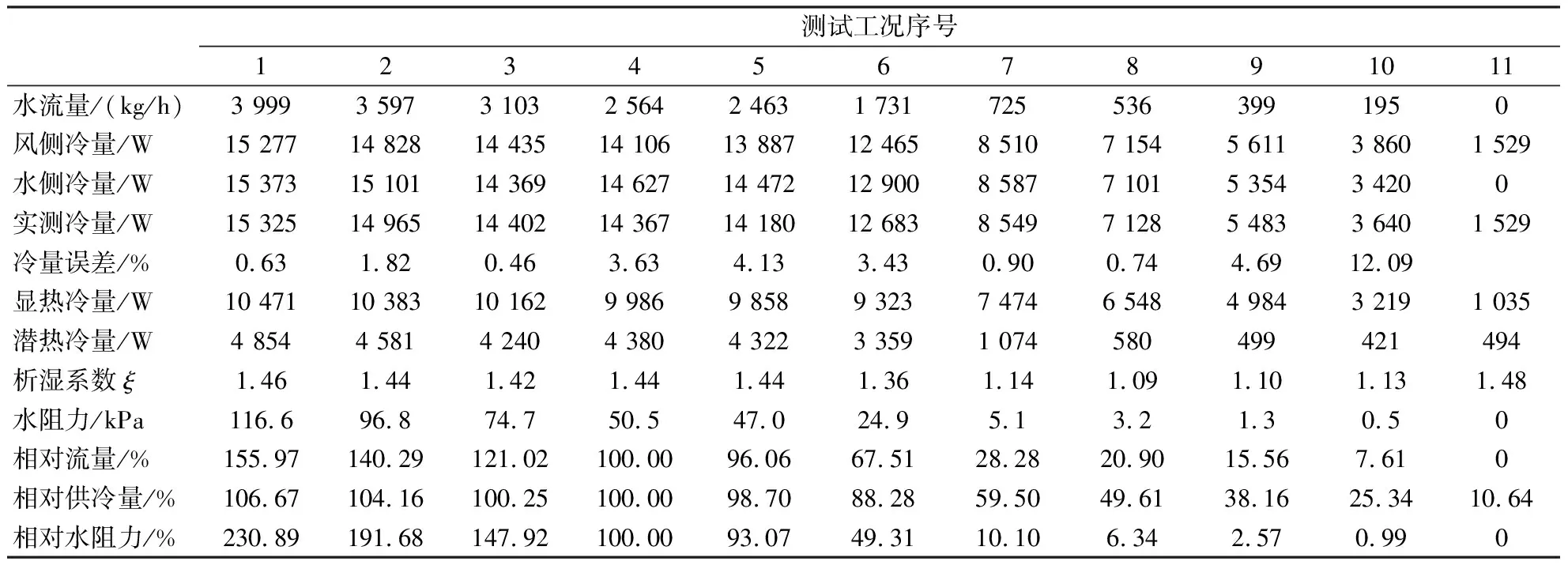
表1 风机盘管机组样机测试数据(节录)
图1给出了被测FCU样机在标准试验工况[13]下获得的变流量换热特性曲线。

图1 FCU试验样机换热特性曲线
需要强调的是,FCU样机换热特性q=f(g)试验过程中,进风空气状态依据GB/T 19232—2003的规定始终稳定在干球温度27 ℃、湿球温度19.5 ℃的标准工况,并非采用试验样机对室内空气处理的结果;输入变量——冷水流量Gw的调节完全由实验者人工给定,与变流量控制技术无关,即与房间冷负荷率并无关联。图1中相对显热量和相对潜热量均为与总供冷量的比值,供、回水温差为被测风机盘管机组样机进出水温差。
2 热工能量平衡
表冷器的热工计算涉及参数较多,计算方程组也不同,计算过程显得相当复杂[14]。张伟等人认为,根据能量守恒原理,水侧增加的能量应等于风侧减少的能量,如式(1)所示[15]。
3 600Gwρcpw(tw2-tw1)=KsFΔtm
(1)
式中Gw为冷水流量,m3/h;ρ为冷水密度,kg/m3;cpw为冷水比定压热容,J/(kg·℃);tw1、tw2分别为冷盘管进、出水温度,℃;Ks为传热系数,W/(m2·℃);F为传热面积,m2;Δtm为空气侧与冷水侧的对数平均温差,℃。
赵文成认为,根据式(2)可以计算出末端设备的瞬时换热量[16]:
Q=Gwρcpw(tw2-tw1)
(2)
为了避免争议,试验依据GB/T 19232—2003规定的FCU供冷量试验与计算方法分别计算得出风侧供冷量Qa和水侧供冷量Qw,其中Qw为扣除风机瞬时输入功率N之后的供冷量,且规定两侧热平衡偏差≤5%为有效[13]。
3 换热时间对换热特性的影响
从时间维度看,除了q=f(g)函数关系之外,供冷量还是换热时间τ的函数q=f(g,τ),在研究表冷器换热特性时需要充分考虑换热稳定时间τd对供冷量的影响。τd为表冷器供冷量从当前稳态到达下一个新的稳态所需要的时间。
GB/T 19232—2003不仅约束了FCU额定供冷量的试验工况参数,还在规范性附录B中规定了风机盘管机组供冷量的试验装置和方法。如第B.3.3条规定:“在试验系统和工况达到稳定30 min后,进行测量记录”。这里的“稳定”应指风与水“两侧热平衡偏差应在5%以内”[11]。试验中通过调节阀的控制可以使被测样机的输入变量(Gw)瞬间发生变化,但无论是风侧还是水侧输出变量(Qa、Qw)的变化均滞后于输入变量(Gw)的变化。当Gw从前一稳态调节至当前稳态后,Qa、Qw各自依旧持续地从前一稳态向新的稳态变化,在满足两侧热平衡偏差≤5%或回水温度tw2及两侧供冷量均达到稳定的最大值之前,tw2、Qa和Qw均为持续变化量。例如,试验中相对流量g由67.51%降低至28.28%,相应地,tw2由13.48 ℃持续升高,最终稳定在17.48 ℃,稳定耗时>30 min。即使Gw为定值,FCU总供冷量仍为渐变量,相对供冷量q与相对流量g之间并非单值函数关系,即q=f(g)函数中的自变量(g)没有唯一对应的因变量值(q)。
样机试验中曾出现偏差为5.02%~5.20%的情况,致使试验工作终止,待所有试验工况再次调试之后,重新开始。FCU风与水之间的热量传递具有显著的迟滞特性,试验设备中温度传感器等测试元器件也存在热量传递在时间上的迟滞。FCU实现新稳态所需时间τd伴随g的降低而延长,τd≠定值。在大流量(g>100%)区间冷水达到新稳态的时间τw小于空气实现新稳态所需的时间τa,Qw先于Qa趋于稳定;当g≤28.28%时,两侧实现稳态所需时间出现反转,τw>τa。伴随g的继续降低,两侧热平衡所需稳定时间τd显著延长,尤其是冷水进入层流状态之后,实测回水温度tw2变得漂浮不定,两侧热平衡偏差>5%,已无法满足GB/T 19232—2003规定的稳定工况要求。例如g=7.61%时两侧实测供冷量偏差已经高达12.09%,且τd>120 min仍无法稳定。当Gw=0时,FCU出风干球温度ta2=25.81 ℃,湿球温度为18.93 ℃,回水温度tw2=25.27 ℃,供回水温差Δtw=18.2 ℃,实测Qa=1 529 W,即g=0时q=10.64%。在高挡风速工况下持续390 s后出风干球温度ta2逼近27.0 ℃,其逼近程度已超出试验设备温度传感器精度范围,难以读取和记录,风与水两侧最大换热温差Δtmax=20.02 ℃,最小换热温差Δtmin=0.54 ℃,潜热供冷量依旧大于0,显热供冷量主要用于抵消风机发热量。
试验表明,FCU风与水两侧热量传递迟滞所需要的时间对其换热特性q=f(g)的影响应引起包括FCU在内的表冷器研究者和应用者的充分重视。在变流量冷水系统实际运行中,常常是前一个热平衡尚未稳定,下一个流量的变化就已经完成了。变化相对缓慢的回水温度tw2和相对供冷量q始终滞后于瞬时变化的相对流量g,FCU还来不及完全出力,无法呈现出一条完整平滑的换热特性曲线q=f(g)。
从换热学理论出发,基于回水温度tw2或供回水温差Δtw的“小流量,大温差”节能控制技术在基础理论上存在缺憾。撇开其他因素的影响,仅就试验样机风与水两侧热平衡所需时间τd>30 min的基本事实,即令基于回水温度tw2控制、供回水温差Δtw控制,以及非线性补偿控制理论和等百分比自动控制技术[1,16-19]难以适应。
4 流动特性对换热特性的影响
李玉街等人认为,“由于层流过程中各流层之间没有混合地同向流动,在这种状态下几乎没有换热现象发生,则流出换热设备的水温与流入的水温完全相同”[18]。但是,在标准工况[11]条件下,试验样机FCU的进风空气状态(干球温度27 ℃、湿球温度19.5 ℃)和供水温度tw1=7 ℃始终是定值。当相对流量g<28.28%(q=59.50%)时,换热管内冷水流速<0.55 m/s,雷诺数趋近3 200,冷水流态视为进入过渡状态[1];当g<20.90%(q=49.61%)时,换热管内流速<0.41 m/s,雷诺数趋近2 320,冷水流态进入层流状态[1]。但tw2始终伴随g的降低而升高,tw2对换热特性q=f(g)和供回水温差Δtw的影响是显而易见的。试验数据显示,当冷水流态进入层流之后,tw2持续保持升高的态势,当g=0时,tw1=7.07 ℃,tw2=25.27 ℃,Δtw高达18.20 ℃(见表1),始终未能重现tw2=tw1的现象,与“流出换热设备的水温与流入的水温完全相同”[18]的结论相悖。
从换热学理论出发,只要两侧换热温差Δt0>0 ℃,换热现象就不会停止。冷水流态进入层流状态后,由于回水温度tw2长时间难以稳定,当Gw为定值时,Qw没有唯一对应的稳定的Δtw(tw2-tw1)值,公式Qw=Gwρcpw(tw2-tw1)需谨慎使用。
5 供水温度对换热特性的影响
蔡宏武认为,供水温度tw1升高1 ℃,即使将末端表冷器的资用压力提高300%,也不能保证其实现100%出力,随着tw1的提升,g=100%时对应的q却不断下降[20]。对FCU而言,tw1的升高不但会导致显热供冷量的减少,同时还造成其除湿能力的下降,无法满足设计供冷量Qm的要求。冷水流量Gw的增加难以弥补表冷器因供水温度tw1升高所导致的风与水两侧换热温差Δt0推动力的降低,而随之而来的水阻损耗和末端资用压头的提高则与冷水节能运行的初衷相悖。
末端FCU风侧供冷量Qa的衰减将造成末端供冷时间的延长,不仅降低了末端供冷服务的质量,还存在末端实际能耗恶化的风险。
6 关于q=f(g)应用的几个问题
6.1 供冷量与需冷量
大温差变流量控制技术通过减小流量可以实现降低管网压力损失、降低循环水泵运行能耗的目的,获得众多自动控制商的青睐。李玉街等人认为,式(2)不仅适用于整个水系统,也适用于任何一个水力环路。因为空调系统的冷负荷与冷水系统流量和供回水温差成正比,冷水所提供的冷量与末端负荷的需求是否匹配,直接反映在环路的回水温度tw2或温差Δtw上。当tw2或Δtw等于其设定值时,则表明所提供的冷量与末端冷负荷的需求相匹配。所以将tw2或Δtw作为被控制变量,可以获得正确的控制结果[18]。但问题的实质是末端表冷器的风侧供冷量Qa与冷水流量Gw和供回水温差Δtw之间并不存在线性关系,Δtw反映的是冷水侧供冷量Qw的变化,并非表冷器实测供冷量QL的大小,更不是末端冷负荷实际需求的多少。GB/T 19232—2019规定:QL=(Qa+Qw)/2,其中Qw=Gwρcpw(tw2-tw1)-N[11],故不能将式(2)中的Q定义为空调系统的供冷量或末端实际需求的冷量。
另外,由于换热特性q=f(g)的非线性属性、不确定性和换热稳定时间τd对QL的影响,因此不论是从质量还是数量上看,Q≠QL≠Qa≠Qw。换热学基础理论上的缺失和数量级上的误差是上述空调水系统节能控制算法和控制策略始终难以获得业界普遍认同的根本原因。
6.2 g=0与q≠0
Robert等人认为,变流量调节控制功能的应用意味着表冷器释放的能量可在0~100%之间连续变化[1,16-19],g=0则q=0,若将Gw=0代入式(2),则Q=0。
试验表明,FCU样机在Gw=0时换热系数Ks=11.28 W/(m2·℃),实测供冷量QL=1 529 W,相对供冷量q=10.64%,并不为0(见表1)。在工程实践中由于调节阀多安装在回水管上,FCU管内静止的液体仍然以热传导的方式与供水总管内7 ℃的冷水产生热量传递,尽管FCU风与水两侧换热温差Δt0大小发生变化,但温差推动力Δt0>0 ℃,使得风与水两侧的热量交换持续进行。
“多余冷量”不仅是数量多少的讨论,供冷量是否为0?能否持续而不间断?涉及到对事物本质的认识,视而不见的研究态度影响了人们科学研究的视角和结果。例如,基于g=0则q=0的基本认识,Robert得出了“由于开/关型两通阀不是开就是关,没有基本的节流功能”[1]的研究结论。遗憾的是这一观点被国内文献[16-19]广泛引用。
6.3 平均换热温差值与q=f(g)应用
被测FCU具有分布参数特性,风与水两侧换热流体的温度沿各自流向持续变化,存在温度梯度,是时间和距离的函数。在换热过程中两侧流体没有轴向混合,既非顺流亦非逆流,流体之间的流动方向互相垂直交叉以错流形式实施换热,同时进风空气还释放出相变潜热,产生冷凝水分布于FCU换热壁表面。为了降低计算难度,常用对数平均温差或算术平均温差的集总参数特性去近似计算。
制造厂商依据表1试验数据,采用计算机辅助设计软件对FCU样机的q=f(g)换热特性进行了模拟对标计算,结果见图2。当相对流量g<28%时,模拟结果显示:析湿系数ξ=1.0,该FCU样机完全丧失了对潜热的处理能力。

图2 模拟软件A计算结果
模拟计算与实测数据之间存在明显偏差,陷入“干球温度27.0 ℃、湿球温度19.5 ℃的进风空气在供水温度tw1=7.0 ℃工况下潜热量为零”的悖论,出现本质性的结论谬误。究其原因,具有集总参数特性的平均换热温差掩盖了换热流体温度的分布参数特性。例如,FCU样机设计工况为:进风干球温度27.0 ℃、湿球温度19.5 ℃,供水温度7.0 ℃;出风干球温度14.3 ℃、湿球温度13.9 ℃,回水温度12.0 ℃。最大换热温差Δtmax=20.0 ℃,最小换热温差Δtmin=2.3 ℃,而对数平均换热温差Δtm=10.69 ℃(Δtmax>Δtm>Δtmin)。当然,问题并非是平均换热温差计算公式的错误,而是制造厂商在引用平均换热温差计算结果时忽视了其应用条件。
6.4 q=f(g)模拟计算
工程实践中需要注意的是,许多制造厂商提供的FCU换热特性q=f(g)数据并不是在国家标准规定的试验工况条件下实际测试得出的试验数据,而是通过自己开发的模拟软件计算获得的结果,尤其是表冷器的设计换热特性数据。因此,在FCU采购前应依据项目设计工况下的技术要求实施合同约定。
这类模拟软件通常多被用于表冷器产品的计算机辅助设计,例如:试验样机在额定工况条件下实测供冷量QL=14 367 W,为其设计冷量Qm的111.07%;实测析湿系数ξ=1.44,为设计工况析湿系数ξm的120%;实测流量G0=2 564.2 kg/h,为设计流量Gm的115.44%。流量增加导致实测水阻损失高于标称值。笔者参与的海西某超高层工程项目中,曾遇到制造厂商用供/回水温度7 ℃/12 ℃模拟计算5 ℃/12 ℃表冷器技术参数的案例。
7 结论
试验样机在标准工况下获得的试验数据为今后FCU在部分负荷工况下变流量调节控制的研究和分析,以及空调冷水系统末端设施的节能控制和调适优化技术的持续研究提供了基础数据。
1) 确定试验工况是试验研究包括FCU在内的表冷器换热特性q=f(g)的必要条件。
2) 标准试验工况参数条件下获得的既有FCU换热特性q=f(g)与房间部分冷负荷率无关。
3) 式(1)、(2)不能直接用于末端空调设备机组供冷量的计算和分析。
4) GB/T 19232—2019规定了FCU标准工况供冷量测量和计算方式,表冷器风与水两侧换热时间的迟滞属性应引起研究学者的重视。
5) FCU冷水的流动特性会对变流量节能控制技术在小流量工况下的应用产生影响,当冷水流态进入层流后,由于回水温度tw2长时间难以稳定,基于tw2或Δtw的“大流量小温差”控制技术面临挑战,理论公式(2)应谨慎运用。
6) 由于换热特性q=f(g)的非线性属性、不确定性和换热稳定时间τd对QL的影响,故Q≠QL≠Qa≠Qw。
7) FCU风与水两侧换热温差Δt0>0 ℃,换热推动力使得表冷器的换热现象不会停止,即便是冷水流量Gw=0(g=0)。
8) FCU换热特性分析研究和模拟计算时,平均换热温差计算结果的应用需注重其应用条件。
