基于PSO 优化的冷凝器模型参数辨识

杨东润 赵星凯 刘忠晨 张 迎 孙 梅

（山东建筑大学，山东 济南 250101）

1 概述

空调中制冷机组的运行效果决定了空调工作性能的好坏，而冷凝器在空调制冷系统中将制冷剂由气体转换为液体，对整个空调系统运行起到了至关重要的作用[1]。因此，建立一个准确的冷凝器模型用于数值预测和空调系统的控制是具有现实意义的。一般而言，对冷凝器的建模方法可分为理论建模和数据建模[2]。基于制冷剂热量交换的合理假设，文献[3]用热力学的方法对冷凝器建立了稳态模型。文献[4]则是根据能量守恒和支持向量机建立了冷凝器的数据驱动模型。文献[5]基于工况假设建立了冷凝器的热力学模型并用LM最小二法对模型的参数进行实时辨识。

随着人工智能和大数据的发展，有越来越多的启发式多目标算法应用到数据集的训练过程中。粒子群优化算法（PSO）作为群体智能的优化方法，具有易实现、调参少、运行速度快等特点，在空调系统中的建模与优化中应用广泛。文献[6]采用改进的PSO 算法，对空调压缩机模型参数进行了优化，使所得模型更加准确。文献[7]基于模型工况的假设，将压缩机模型参数辨识问题转换为带约束的最小化问题，并用粒子群算法求出最优解。

然而，PSO 算法往往会因为初始粒子即初始解选取的不当，导致算法运行后陷入局部最优。因此，本文将离线辨识出的参数结果和参数约束条件作为PSO 中粒子位置的上下边界并初始化粒子进行迭代寻优从而在线辨识出蒸发器模型的最优解。

2 辨识方法

第二步：计算每个粒子的目标函数值作为个体最优解Pbest，取其中目标函数值最小的粒子作为初始全局最优解gbest。

第三步：通过下式迭代更新每个粒子的速度和位置，并计算当前的个体最优解和全体最优解。

第四步：若满足最大迭代次数，则算法终止，输出结果。

3 模型验证

为了验证所提参数辨识方法的有效性，本文采用的冷凝器模型结构为文献[5]所提出的模型，并分别计算与LM最小二乘法所辨识模型的相对误差与平均相对误差。模型结构如下式所示。

表1 各传感器型号、测量范围、测量精度

本文的观测数据为压缩式制冷系统运行各传感器所采集的数据，其主要由压缩机、冷凝器、电子膨胀阀、蒸发器所构成的闭合回路，传感器分布与工艺流程图如图1 所示。

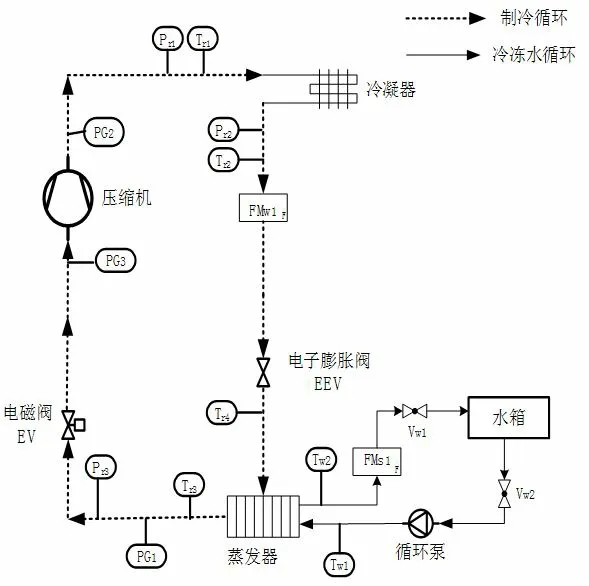
图1 压缩式制冷工艺流程图

进行参数辨识时，由于该模型是稳态模型，所以需要采集系统在稳态下的数据。分别采用LM最小二乘法和PSO 算法得出所需的模型参数后，分别从观测数据集中随机筛选16 个数据并计算不同方法下的相对误差和平均相对误差。计算公式如下。

用LM 最小二乘法和PSO 算法辨识的模型参数如表1 所示，所选拟合点计算的相对误差如图1 所示。

表1 模型参数与相对误差

由图2 可知，本文所提的方法在观测数据相同的情况下辨识的参数值比LM最小二乘法更精确，相对误差更小。根据此，本文将模型输出数据和实际测量所计算的冷凝器热负荷做了对比，结果图如图3 所示。

图2 两种方法计算的相对误差

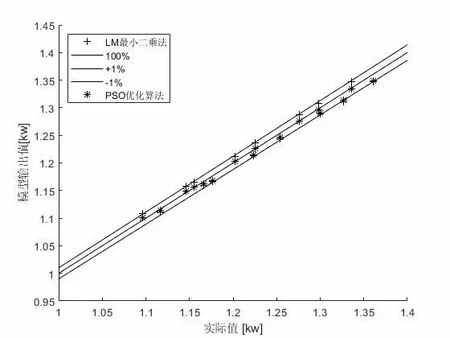
图3 模型输出和原始数据对比结果图

从图3 可以看出通过改进的粒子群算法所得的模型基本与真实计算所得的热负荷吻合。

4 结论

本文根据实测数据并采用冷凝器的混合模型，通过改进的粒子群算法对模型中的未知参数进行辨识。仿真表明，所改进的粒子群算法在参数辨识的准确性上比最小二乘法更为精确，计算出的值更符合实际计算出的热负荷。