大圆航线可执行航向的自动化建模计算∗

王书晓 黄 谦 李 伟

（海军大连舰艇学院 大连 116018）

1 引言

在大洋航行中，采用大圆航线可以大幅缩短航程，提高人员物资投送效率。据粗略测算，由于全球变暖，北冰洋的海冰正加速消融，在不远的将来北极航线将完全开通［1］，恒向线航线的效率、适用程度大大降低，大圆航法将大有用武之地［2］。航海自动化的高速发展要求大圆航线设计的快速化和准确化，为了提高远洋舰艇的航海保证能力，大圆航线可执行航向的自动化计算成为一项重要的时代课题。

2 大圆航线执行原理

根据地图投影原理，大圆航线在用于保障航行的墨卡托海图上是一条弧线，如图1弧AB所示，除非与经线或赤道重合，大圆航线上各点与经线的交角均不相等，也就是说，大圆航线上各点的航向是变化的，舰艇若想要严格沿大圆航线航行，必须不断改变航向，驾驶操纵甚为不便。因此，在航海实践中，通常是按照一定原则把大圆航线分段，在各分点之间沿恒向线航行，即以多条恒向线连接而成的折线来近似代替大圆航线，分为切线法和弦线法两种，如图1中实线所示，即为实际执行的恒向线航线。

2.1 切线法

如图1中折线A-C-D-E-F-B所示，舰艇在起航点A以大圆航向作为恒向线航向航行，航行一定航程之后到达新的转向点C，舰艇必然偏离了原大圆航线一定距离，此时以C作为新的大圆航线起点重新计算从C到B的大圆航向，再作为恒向线航向航行，依此类推，直至到达终点。切线法主要解决两个问题：

图1 大圆航线实际执行原理示意图

1）初始大圆航向计算；

2）以大圆航向作为恒向线航向采用恒向线航法计算到达点坐标。

2.2 弦线法

如图1中折线A-H-I-J-K-B所示，通常按经度间隔5或10，或按大约一昼夜的航程，在大圆航线上确定若干个分点作为转向点，舰艇沿相邻两分点间的恒向线航行。弦线法主要解决的问题是：

1）按经差或航程间隔对大圆航线进行分段时分点坐标的计算；

2）分点之间采用恒向线航法计算航向航程。

无论采用何种方法，初始大圆航向的计算和弦线法分点坐标的计算是大圆航线自动化计算中的瓶颈问题。

3 基本参数计算

地球的实际形状很不规则，在航海上通常取旋转椭球体或圆球体作为地球的近似体进行数学计算，由于大圆航线航程较长，一般可达数千海里，椭球体曲率的影响相对较小，因此在进行大圆航线计算时，可把地球看作圆球体，运用球面三角形公式进行大圆航线的解算。

3.1 大圆航法三角形基本要素

在球面上，由三条大圆弧所围成的球面图形称为球面三角形，三条边和三个角均大于0°、小于180°的球面三角形称为欧拉三角形，也就是航海上所用的球面三角形［3］。在大圆航法中使用的欧拉三角形，是过地球表面A、B两点的经线与连接A、B两点的大圆劣弧所围成的球面三角形，如图2中三角形PNAB，其中连接A、B两点的大圆劣弧即为A点到B点的大圆航线。

3.2 大圆航程计算

如图2所示，在球面三角形PNAB中，由于已知启航点A和到达点B的经度、纬度，可知［4］：边PNA的长度等于A点的极距90°-j1，边PNB的长度等于B点的极距 90°-j2，角 APNB 等于 A、B 两点的经差∆λ，两点之间的大圆航程时也就是AB边的长度，可采用球面三角形的“余弦公式”计算［5］：

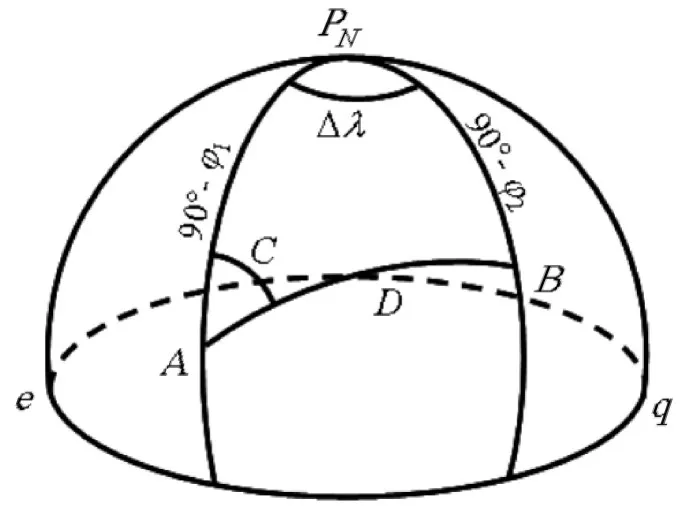
图2 圆球体面上的大圆航线示意图

式中：φ1为A点纬度，φ2为B点纬度，规定北纬为“+”，南纬为“-”；∆λ为经差，规定东经为“+”，西经为“-”，D为大圆航程。

3.3 初始大圆航向解算

初始大圆航向是指大圆航线在A点的切线与经线的夹角，也就是地球表面过A点的经线与AB间大圆航线这两个大圆弧所在平面所夹的二面角，因此可利用“余切公式”根据出发点纬度、到达点纬度、两点间经差求得A点的初始大圆航向：

其中：C为初始大圆航向。

在计算机编程中，反余切函数值范围为-90°～90°，计算结果需转换为圆周航向，较为繁琐，而大圆航线与恒向线航线不同，恒向线航线计算时可以根据两点间经差和纬差来判断航向所在象限，进而转换为圆周航向。在大圆航线上，纬度的变化规律比较复杂，不能用纬差来判断航向所在象限，需借助人工判断，为克服此项弱点，模型引入“正弦公式”进行计算：

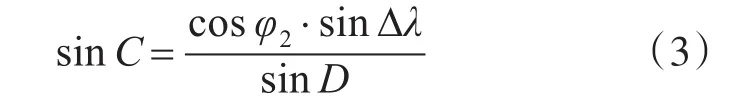
由于大圆航程D是个未知量，需通过计算获得，不但徒增计算误差，而且无法判断航向所在象限。可以考虑用余切函数的绝对值来求出象限法航向值，同时根据航向的余切值和正弦值来判断航向所在象限，规则是：

若ctgC、sinC均为正，为NE象限；

若ctgC、sinC均为负，为NW象限；

若ctgC为负、sinC为正，为SE象限；

若ctgC为正、sinC为负，为SW象限。

以上判断方法全球适用。

4 分点坐标计算模型

传统的分点坐标计算方法巧妙运用了球面直角三角形计算简便的特点，利用大圆航线顶点来计算分点坐标［6］，降低了三角函数计算难度，具有很大的实践优越性。但是，计算步骤过多，需要首先计算顶点坐标才能求得分点坐标，而且不能根据航程间隔进行分点。为了适应航海自动化的发展，需要建立更有利于计算机编程实现的分点坐标计算模型［7］。

4.1 按经差分段时分点坐标计算

按经差对大圆航线进行分段是制定大圆航行计划时较常用的方法［8］，其中大圆航线起点坐标已知，确定了用于分段的经差，相当于给出了各个分点的经度，需要求解的就是各分点的纬度。

如图3所示，已知A点纬度φ1，初始大圆航向C，设E点为第n个分点，根据分点原则求得E点与A点间的经差∆λn，即可采用“余切公式”，计算出E点的纬度φn：

图3 大圆航线分点计算原理示意图

重复使用以上函数，即可计算出所有分点的坐标。

4.2 按航程分段时分点坐标计算

采用弦线法按航程间隔对大圆航线进行分段时，为了保证分点坐标在大圆弧上，航程间隔应是大圆航程，而在一般的大圆航法仿真计算软件中，通常是按照恒向线航程进行迭代运算，逐次逼近［9］，这样处理计算量增大，而且不符合图上作业过程，不能通过图上作业来检验模型的正确性，也不能把计算结果作为教学训练中的考核标准使用。

1）分点纬度的计算

假设分点E与A点之间大圆航程为∆D，根据已知条件初始大圆航向C、A点纬度φ1，采用“余弦公式”，可求得E点的纬度φn：

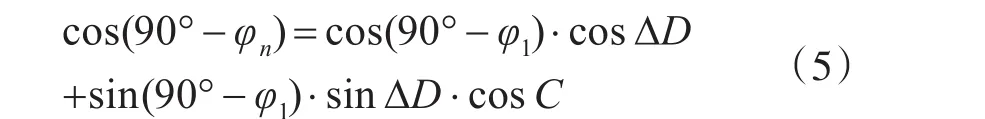
2）分点经度的计算

与纬度计算一样，根据初始大圆航向C、A点纬度φ1、E与A点之间大圆航程为∆D，采用“余切公式”即可求得E与A点之间的经差∆λn：

5 计算效能分析

5.1 软件计算流程设计

根据航海实践中实际执行大圆航线的基本原理，可以分三种情况构建大圆航线计算流程：指定经差弦线法、指定航程间隔弦线法、指定航程间隔切线法［9］，前文已经给出了全部计算模型。指定经差弦线法的计算流程如图4所示，根据该流程图和计算模型即可编写大圆航线设计软件，输出分点坐标和实际执行的恒向线航向航程［10］。

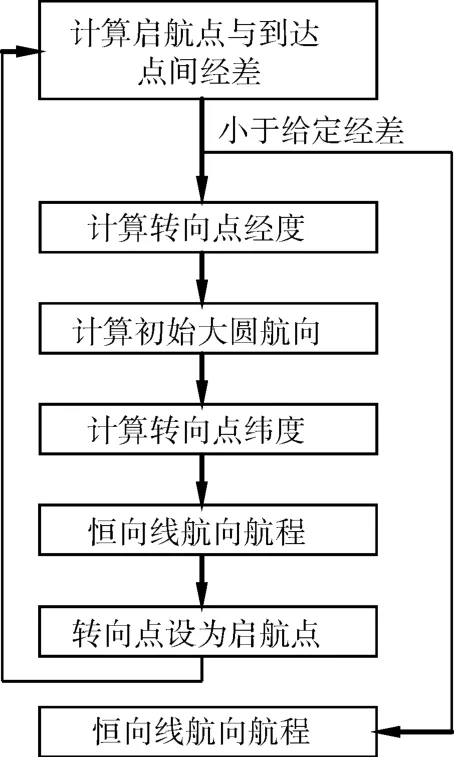
图4 指定经差弦线法计算流程

5.2 计算结果分析

以远洋船舶经常采用的一条横跨北太平洋的东行大圆航线为例：起航点为东京附近的A点（φ35°00'.0N，l143°00'.0E），到达点为美国旧金山附近的B点（φ38°00'.0N，l125°00'.0W），若采用弦线法拟定大圆航行计划，分别按照经差10°和航程间隔600'计算，结果如表1、表2所示。在航海实践中采用给定经差的弦线法时，为了方便计算，通常第一个转向点的经度取到整5°或整10°，设计软件时可进行同样的处理。

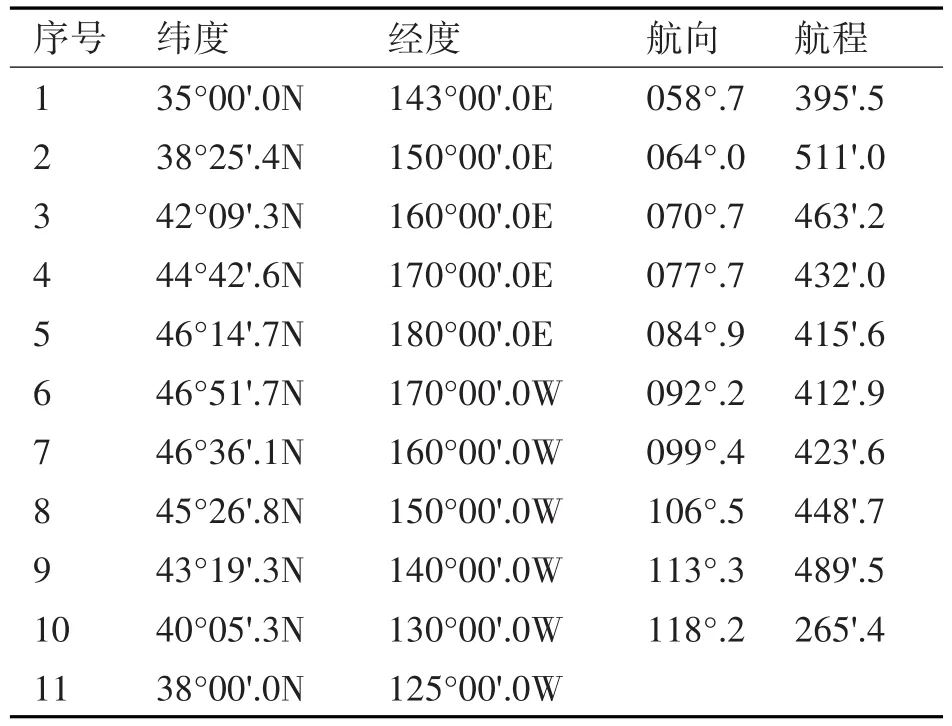
表1 经差10°按弦线航行的航线计划表

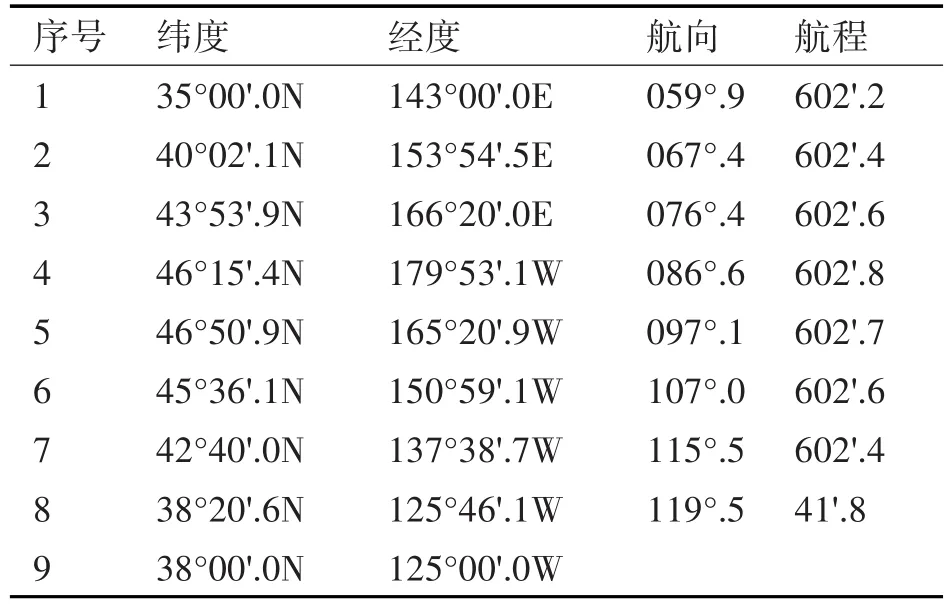
表2 航程间隔600'按弦线航行的航线计划表

通过与大圆航法海图作业结果比对，计算出的分点均位于大圆航线上，且经差间隔或航程间隔完全符合要求，与图上作业结果一致。计算结果，两点之间的恒向线航程4459'.2，大圆航程4241'.7，按照经差10°进行分点时总航程为4257'.4，比大圆航程增加0.37%，比恒向线航程缩短4.53%；按照600'航程间隔进行分点时总航程为4259'.5，比大圆航程增加0.42%，比恒向线航程缩短4.48%。从以上结果还可以看出，实际执行大圆航线时，分点越多，实际航程越短，越接近大圆航程，但会增加转向次数。

6 结语

立足于航海工作实际，系统研究了大圆航线计算模型，从计算机编程实现的角度进行了细化和补充［11］，重点解决数学模型在实用中的细节问题，使模型更加完善、更加实用［12］，在近几年海军训练舰编队出访南太平洋、郑和舰单舰环球行等远洋航海实习任务中进行了大圆航法教学和训练时，依据此模型设计的软件成功运用于舰船跨洋航线航行计划的拟定，同时用于航海专业教学中，有效提高了教学训练效果，有较高的实用价值。