基于多传感器的双机编队相对定位算法研究∗

杨少帅 郑 威

（1.中国西南电子技术研究所 成都 610036）（2.73602部队 南京 210000）

1 引言

相对导航技术是编队飞行器或网络成员间相对位置确定的一项关键技术［1～2］。广泛应用于编队卫星高精度的相对位置确定、航天器交会对接、战斗机编队飞行、无人机自主着舰、自主空中加油等领域［3～4］。目前国内相对导航的研究主要集中在基于惯性与相对测距的相对导航［5～8］、基于伪距差分的相对导航［9］、基于卫星和惯导组合的定位导航［10］，但是没有将卫星导航差分的高精度、惯性导航的自主性鲁棒性以及测距测角信息的直接测量有效地结合起来。

惯性导航系统具有运行的自主性，能够连续提供载体的位置、速度和姿态信息，但是测量误差随时间累积，需要初始对准和不断修正。卫星导航系统精度高，但信号容易受阻挡、干扰，信号中断后需要数秒的重新捕获时间。卫星导航与惯性导航系统，两者结合，取长补短，是公认的理想的组合导航方式［11］。协同成员间，基于时间同步技术和天线技术，可以获取相对距离信息和相对角度信息。以惯导作为公共参考源，进行传感器数据的滤波预测，并融合多源数据，提供一种可靠性好、精度高、鲁棒性强的相对导航解决方案［12～13］。

本文以长机-僚机编队的情景为例，基于相对运动误差方程，推导了伪距差分、相对测距测角观测方程。利用联邦滤波器，估计相对位置、速度、姿态状态。在传感器观测量都可用的情况系下，融合多源信息，得到精度高、可靠性好的结果；在卫星导航差分结果不可用的情况下，仅利用惯导和测距测角，保证相对导航精度，并通过仿真验证该方法的有效性。

2 相对导航方程

相对导航方程根据相对运动学关系推导而来，由相对姿态、相对位置、相对速度、以及陀螺、加速度计的漂移构成。由于误差状态方程滤波后精度高，所以本文先给出相对状态方程，再给出相对误差状态方程，并利用误差方程进行求解。

2.1 相对状态方程

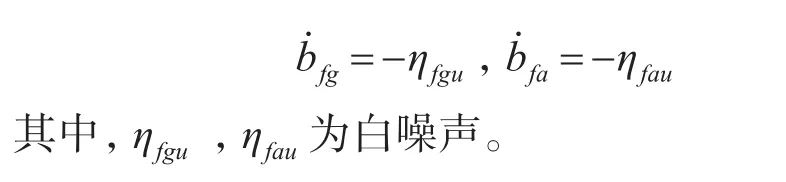
2.2 相对状态误差方程

3 相对导航观测方程

3.1 伪距差分观测方程

采用伪距差分方法时，长机并不单独解算自己的绝对位置，而是将得到的伪距观测量，通过链路传到僚机，由僚机统一进行处理，如图1所示。长机和僚机同时获得相对于同一颗导航星的伪距进行差分。

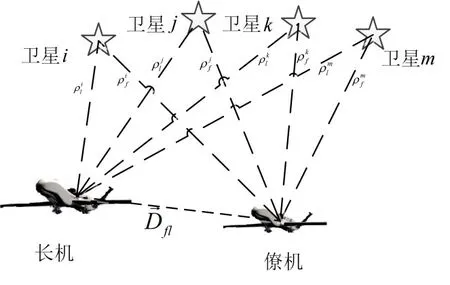
图1 伪距差分

将由伪距差分计算的观测值Z∆ρ与通过INS计算得到的相对伪距观测值相减，推导伪距差分观测方程。

3.2 测距与测角观测方程

4 多传感器信息融合

4.1 联邦滤波器

相对导航手段除了传统的INS，卫导之外，还可利用测距、测角的等传感器。多种观测量的信息需要一种有效融合方式。多源组合导航系统滤波结构主要有集中滤波和联邦滤波，集中滤波精度高、实时性好，但易受干扰；联邦滤波容错能力强，便于故障诊断与隔离。多传感器相对导航的算法结构如图2所示。

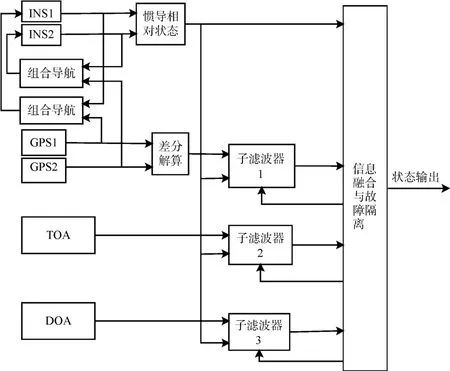
图2 多传感器相对导航算法结构图

子滤波器1、2、3为标准卡尔曼滤波，主滤波器由三个局部滤波器得到各自得到相对状态误差估计值后，再在主滤波器中根据信息分配的原则进行融合可得最终相对状态误差估计值，融合过程如下：

式中：X1(k/k),X2(k/k),X3(k/k)分别是子滤波器1、2、3输出的相对状态误差估计值，P1(k/k),P2(k/k),P3(k/k),PM(k/k)分别是子滤波器1、2、3和主滤波器的滤波误差方差阵。

4.2 故障检测策略

假设有n个传感器，每个传感器的测量模型：

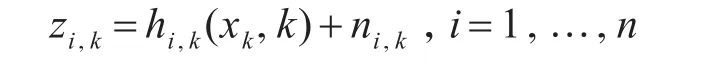
ni,k是高斯白噪声。

故障传感器的自主检测隔离是多种传感器的融合系统的可靠保障，可以通过新息矢量vk来检验传感器数据的有效性，首先归一化的新息矢量为整主滤波器的信息分配系数，并结合残差χ2检测的检测结果，达到在相对较大故障时隔离故障的效果。

5 算法仿真

5.1 仿真条件

利用轨迹发生器产生长机和僚机的理想惯导数据，在此基础上，加上陀螺加速度计误差进行惯导解算。测距观测、测角观测以及卫导误差由理想惯导数据加误差计算得到。仿真条件如表1所示。

表1 仿真条件

5.2 联邦滤波仿真

由于惯导自身姿态不准确，所以在计算相对导航误差时，统一长机和僚机的相对导航计算的坐标系，在地固坐标系下统计导航误差。相对导航误差仿真结果如图3所示。

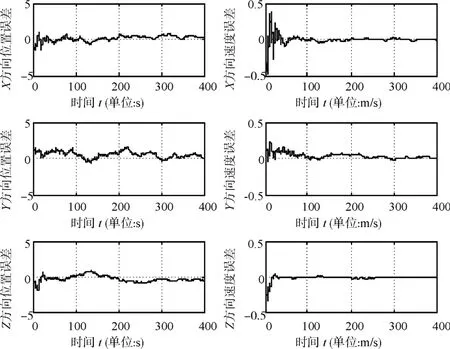
图3 相对导航仿真结果

取200s～400s之间的数据，滤波稳定后，相对导航误差均值和标准差结果见表2。

从图3和表2可以看出，相对位置误差很快就达到1m之内。并且在稳定后，XYZ三向的相对位置误差估计能够稳定在1m之内，相对速度误差能够稳定在0.1m/s内。

表2 相对导航误差统计结果

5.3 差分故障相对导航仿真

由于差分需要长僚机实时交互卫星导航观测数据，而针对链路的不稳定造成的差分解算不稳定而带来的较大偏差的情况下，采用基于χ2检验的方法检测，从而选择性地利用卫导差分观测量。仿真中自200s开始，对伪距差分结果加入100m的随机误差和200m常值误差以模拟卫导差分不可用。仿真结果如图4所示。

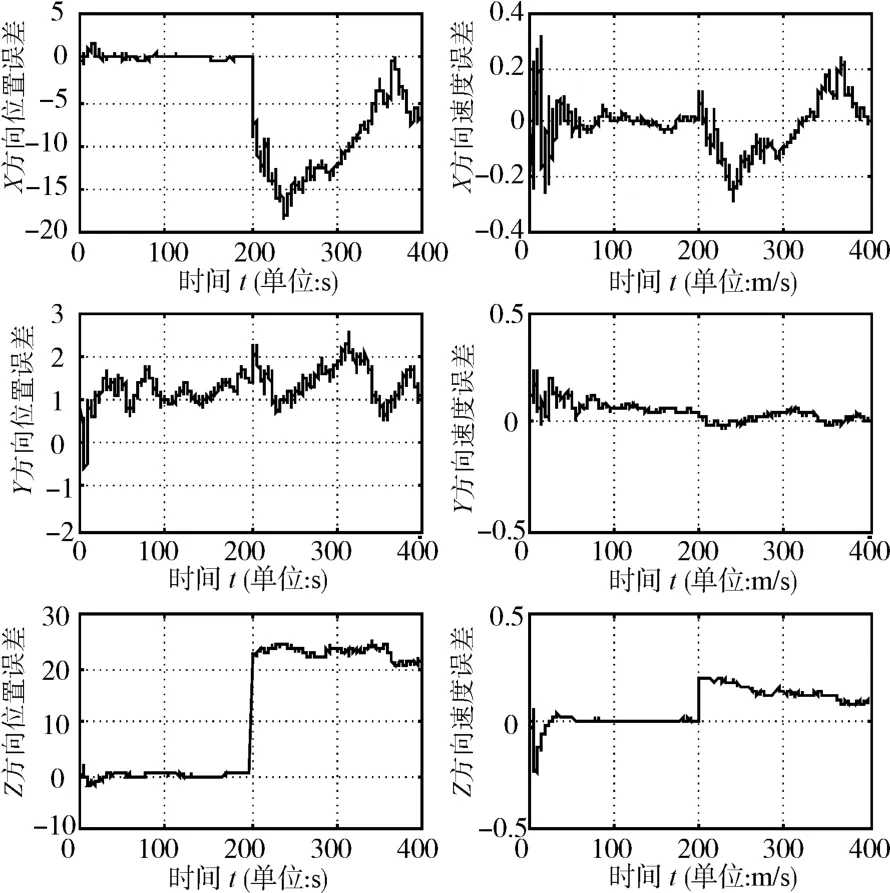
图4 伪距差分出现波动后的仿真结果

从图4中可以看出，相对位置、速度解算误差在200s左右，会出现一定程度上的增大。当伪距差分观测不可用时，仅依靠相对测距和测角与惯性导航的组合方式，相对导航精度会比依靠卫导差分有所降低，但仍然可以在卫星导航信号不可用的时间内，保证相对位置误差在30m以内，相对速度误差在0.5m/s以内。

6 结语

本文建立了相对导航误差模型和伪距差分、相对测距、测角的观测方程，研究了存在多种导航传感器观测量时的相对导航联邦滤波算法。通过仿真分析发现，利用惯导、伪距差分、测距测角融合处理，能够达到亚米级别的相对定位精度。以惯导系统为导航参考的联邦滤波器能够在差分结果不可信赖的情况下，利用相对测量，能够保证相对导航的收敛和系统的鲁棒性。