基于奇异谱分析的GNSS坐标时间序列粗差探测与噪声估计

陶国强

1 东华理工大学长江学院，江西省抚州市学府路56号，344000

1 传统谐波模型

GNSS基准站连续坐标时间序列中蕴含着丰富的信号与噪声。其中信号包含线性信号与非线性信号，线性信号代表基准站由构造应力导致的构造运动，一般以速度场形式表示；非线性信号主要表现为由环境负载导致的测站季节性位移。噪声则包含白噪声与有色噪声。一般以谐波模型来描述GNSS坐标时间序列：

dkcos(2kπti)+e(ti)

(1)

式中，y(ti)为ti历元时刻的基准站坐标，a、b为测站初始位置和速度，ck、dk(k=1,2)为年和半年周期振幅，e(ti)为观测误差。若顾及所有观测历元ti(i=1,2,…,N)，则式(1)可写为：

y=Ax+e

(2)

式中，y、e∈RN×1为观测值及其误差向量，A∈RN×6为系数矩阵，x∈R6×1为未知参数。各变量的构成为：

则参数的最小二乘估值为：

(3)

式中，Σy为观测值的方差-协方差阵。由式(3)可知，要求得最优估值，需已知观测值的协方差阵。目前公认的最优噪声模型为白噪声+闪烁噪声的组合，因此需要估计各个噪声的噪声分量，可采用方差分量估计方法确定。

2 基于SSA的GNSS坐标时间序列粗差探测与噪声估计

2.1 SSA基本原理

对于时间序列{y1,y2,…,yN}，首先选择一个合适的窗口L，将其进行滞后排列：

模板质量控制之一就是要求底面模板的曲线精度符合内拱底缘坐标要求，而且具有足够的强度和刚度，保证在安装钢筋及浇筑混凝土过程中不会变形。为此，首先在模架系统上方铺设10 cm×10 cm方木，在其上方安装底模。底模安装完成后，由测量员对底模高程、曲度进行校核定位，将调整后的拱肋底模进行加固，防止变形。

(4)

式中，K=N-L+1，Y∈RK×L为滞后矩阵。其方差-协方差阵为C=YTY，对其进行奇异值分解：

C=VΛVT

(5)

式中，Λ∈RL×L为对角阵，其对角元λk(1≤k≤L)为C的奇异值，V=(v1,v2,…,vL)为正交阵，vk为第k个特征向量。可通过V和Y确定主成分矩阵：

A=VY

(6)

A的第k个行向量被称为第k个主成分，其第i个元素可由式(7)计算：

(7)

式中，vk,j为vk的第j个元素。由第k个主成分可重构第k个分量：

(8)

则原序列yi可表示成：

(9)

2.2 粗差探测

已有大量研究表明，GNSS坐标时间序列中的粗差主要反映在其噪声(残差)中，因此可直接对噪声序列进行粗差探测。为避免残留信号对粗差探测的干扰，需将信号与噪声进行有效分离。经SSA处理后，GNSS坐标时间序列已被分解为若干能量不等的分量，其中能量较高(轨迹矩阵对应分量的特征值较大)的表示低频信号，能量较低(轨迹矩阵对应分量的特征值较小)的表示高频噪声。本文采用特征值比例法进行信噪分离，取总能量占比90%以上的特征值对应的重构分量作为信号s，剩下的分量作为噪声ε。

原坐标时间序列的粗差大都反映在ε中，将其中的元素进行升序排列。考虑到GNSS坐标时间序列的精度随历元而变化，采用开窗IQR准则进行粗差探测，其判定准则为：

|εi-med(εi-L/2,εi+L/2)|>c·IQR(εi-L/2,εi+L/2)

(10)

式中，εi为ε的第i个分量，med(·)为求中位数算子，IQR(·)为求四分位距算子，L为窗口长度(一般取182)，c为比例因子(一般取3)。因基于IQR准则的粗差探测有较强的边缘效应，式(10)仅适用于序列中部的粗差探测，对于序列两端的粗差探测效果较差。本文对式(10)进行改进，对于边缘数据适当降低c值，将边缘数据非边缘化，则有：

(11)

式中，d=c/3。对残差序列ε进行遍历，以当前值为中心，构建窗口序列，当满足准则(11)时，即认为当前历元观测值为粗差。

2.3 噪声分量估计

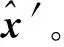
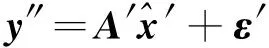
(12)

式中，y″表示生成的新序列。考虑到式(12)严格满足Gauss-Markov模型，因此可采用LS_VCE方法估计噪声分量：

(13)

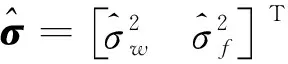
(14)

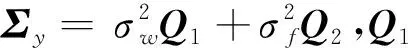
3 算例分析

3.1 模拟数据

为了验证本文算法的正确性，采用模拟的坐标时间序列数据进行验证。模拟策略同文献[9]，即认为GNSS坐标时间序列由3个部分组成：

y(ti)=s1(ti)+s2(ti)+ε(ti)

(15)

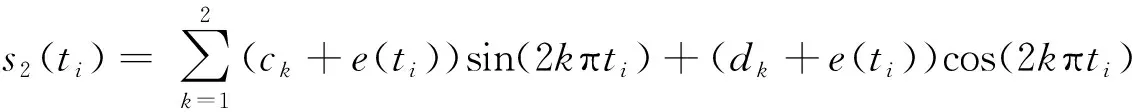
表1 模拟时间序列参数

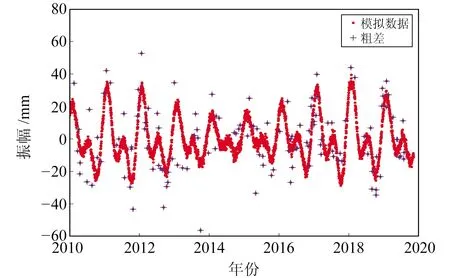
图1 模拟的坐标时间序列Fig.1 The simulated coordinate time series

采用SSA对模拟的坐标时间序列进行分析，窗口长度取365。根据SSA原理构建轨迹矩阵，并求其协方差阵的特征值，结果见图2。由图可见，前4个特征值占总特征值的91%，因此可选择前4个特征值对应的RC作为信号，剩余RC作为噪声。图3和图4分别为SSA和谐波模型分离出的信号与噪声，显然SSA提取出的信号更能反映出时间序列的真实非线性变化，其残差也相对较为平稳；而谐波模型仅能粗略地描述时间序列，其残差中仍然含有部分信号。此外，原始序列中的粗差大都传递至残差中。分别采用传统算法和本文算法探测残差中的粗差，结果见图5。可以看出，传统算法仅能探测到83%的粗差，而本文算法可探测到94%的粗差。

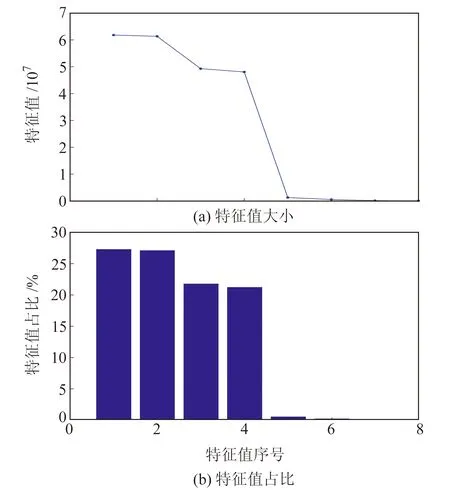
图2 轨迹矩阵协方差阵的特征值及其占总特征值之比Fig.2 The eigenvalues of the covariance matrix of the trajectory matrix and its ratio to the total eigenvalues

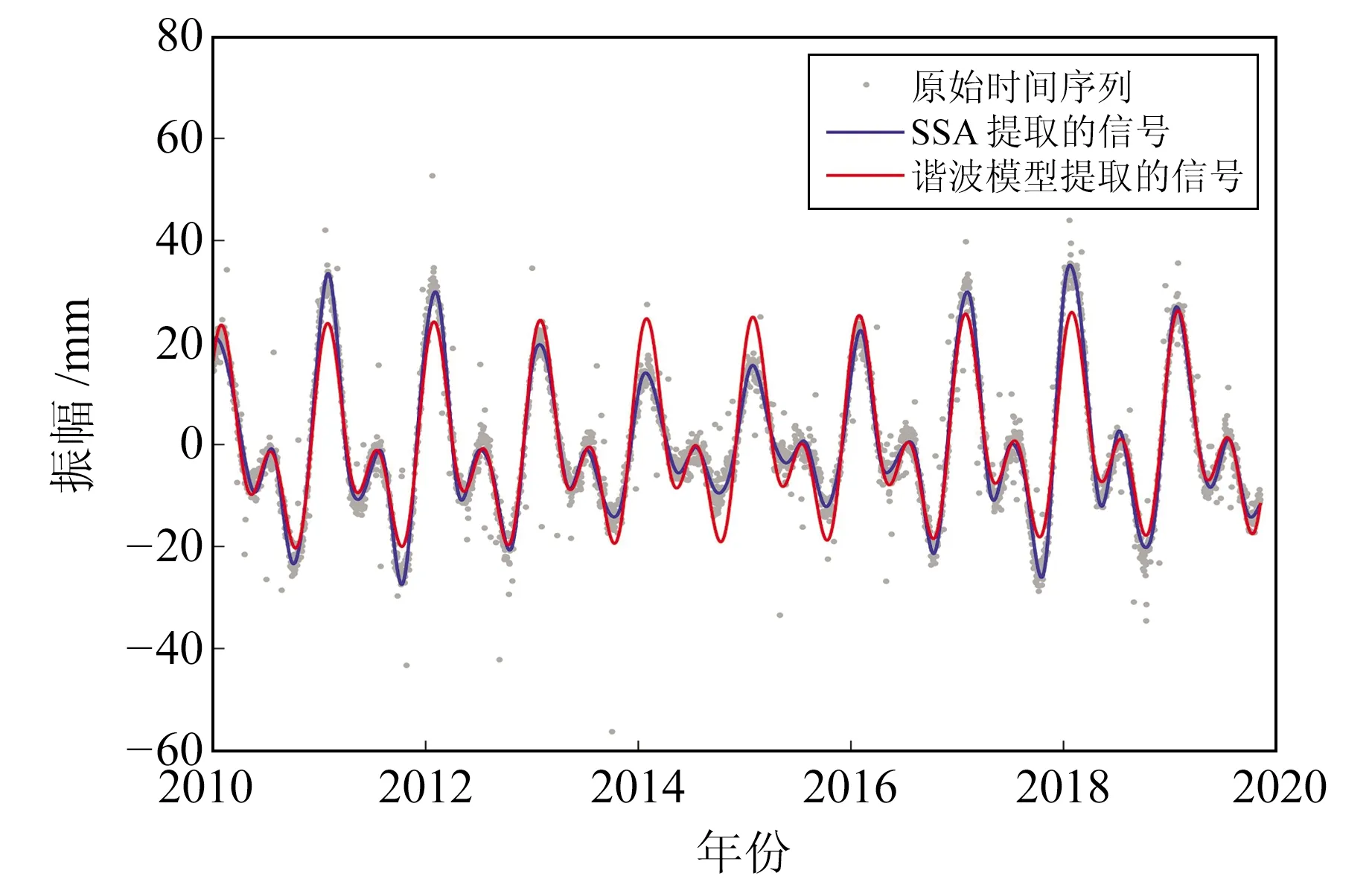
图3 谐波模型和SSA提取的信号Fig.3 Signals extracted by harmonic model and SSA

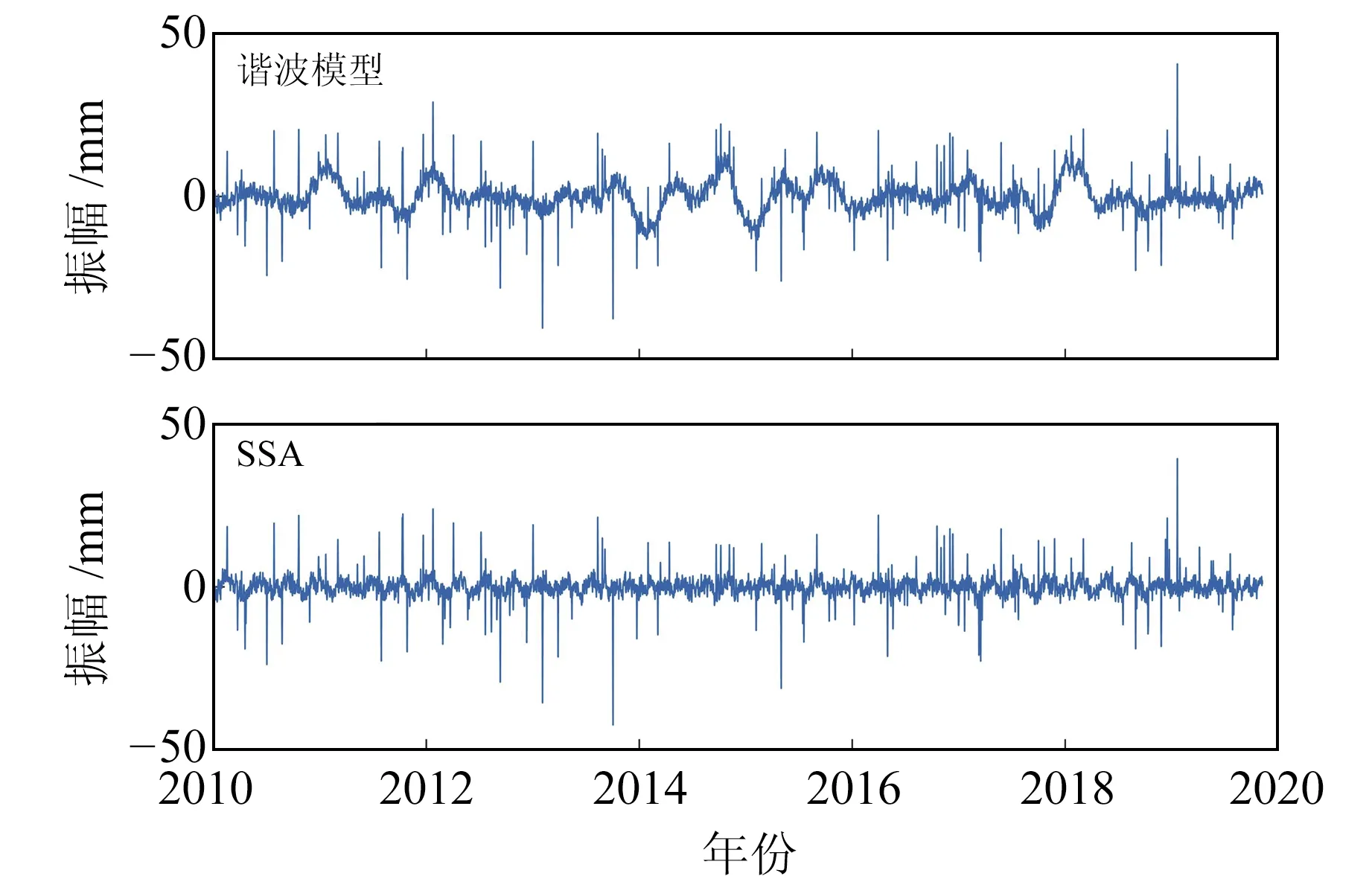
图4 谐波模型和SSA提取信号后剩余的残差(噪声)Fig.4 Residual (noise) after filtering out signals using harmonic model and SSA

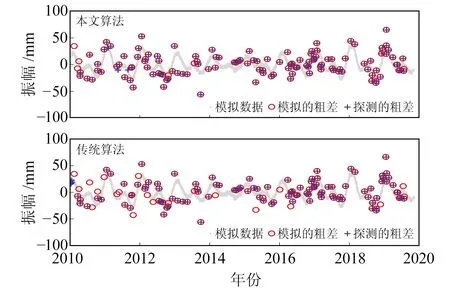
图5 2种算法探测出的粗差与模拟粗差的对比Fig.5 Comparison of gross error detected by two algorithms and simulated gross error

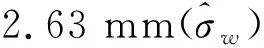
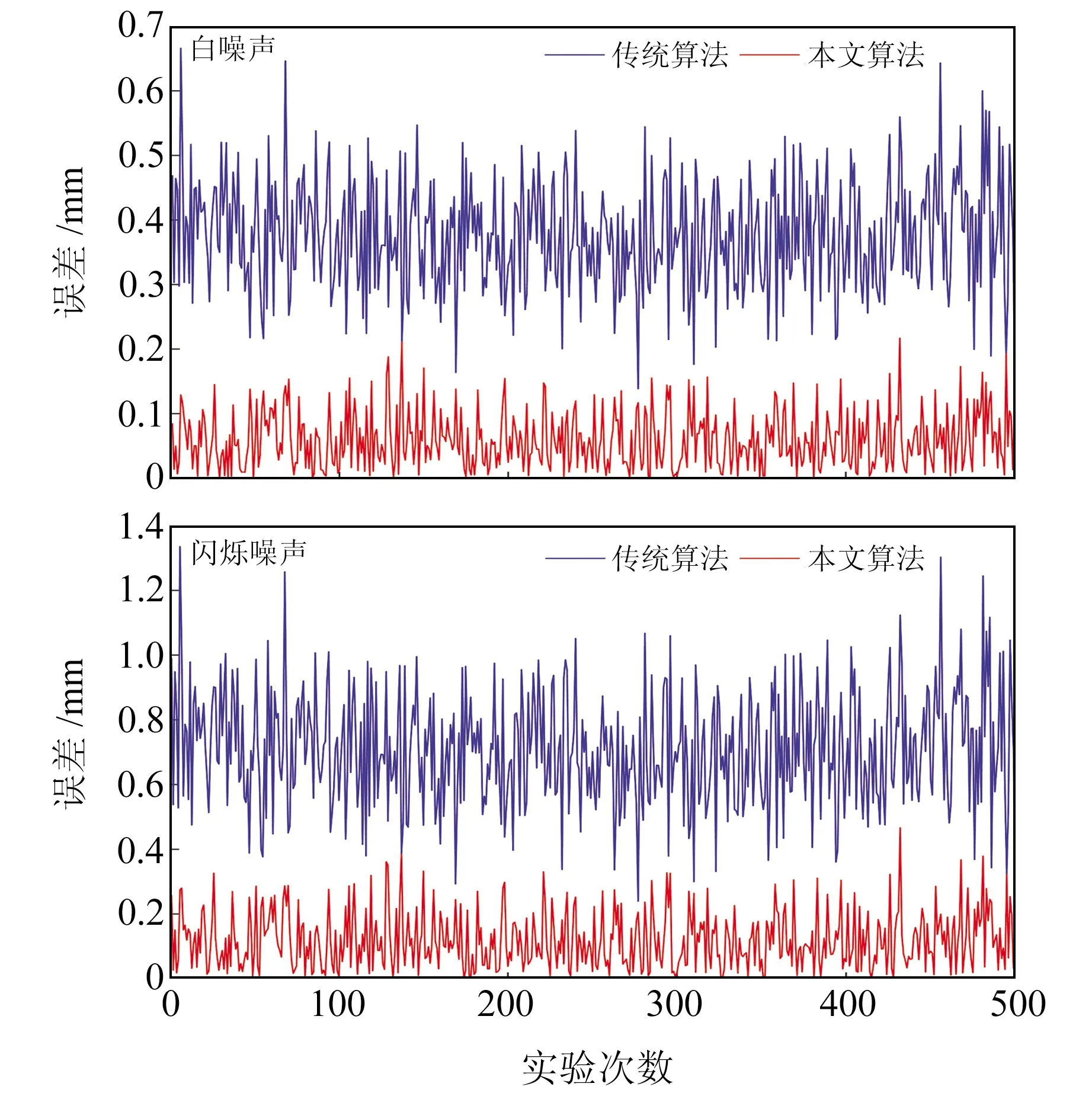
图6 500次模拟实验2种算法估计的噪声分量估值绝对误差Fig.6 The absolute error of noise components estimationsderived by two algorithms for each of 500 simulations

3.2 实测数据

为进一步验证本文算法的有效性，选取陆态网络提供的10个基准站观测数据进行分析。所有数据可通过中国地震局GNSS数据产品服务平台(http://www.cgps.ac.cn/)获取，表2为各站点的相关信息。以LUZH站为例，图7为其1999～2019年的连续观测坐标序列，其中含有大量的粗差，必须剔除。分别采用SSA和谐波模型对去趋势后的坐标序列进行信噪分离，图8为3个方向轨迹矩阵协方差阵的特征值及其占总特征值之比。由图可知，N方向前3个特征值之和占总特征值之比达90.88%，E方向前5个特征值之和占总特征值之比达90.05%，U方向前10个特征值之和占总特征值之比达90.03%。由此可确定，信号分量和噪声分量的分界层分别为3(N)、5(E)和10(U)。2种算法估计的信号如图9所示。可以看出，传统谐波模型仅能粗略地描述GNSS坐标时间序列，特别是对于水平方向的坐标序列，其拟合度较差；而SSA不受正弦波的假定约束，它从时间序列的动力重构出发，能自适应地提取出时间序列的信号，因此其能较好地描述GNSS坐标时间序列的非线性变化。

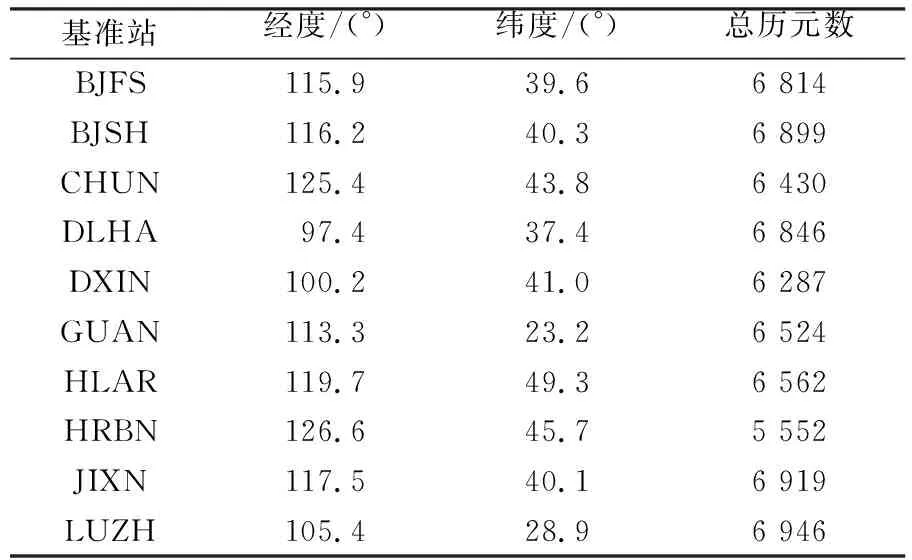
表2 站点信息

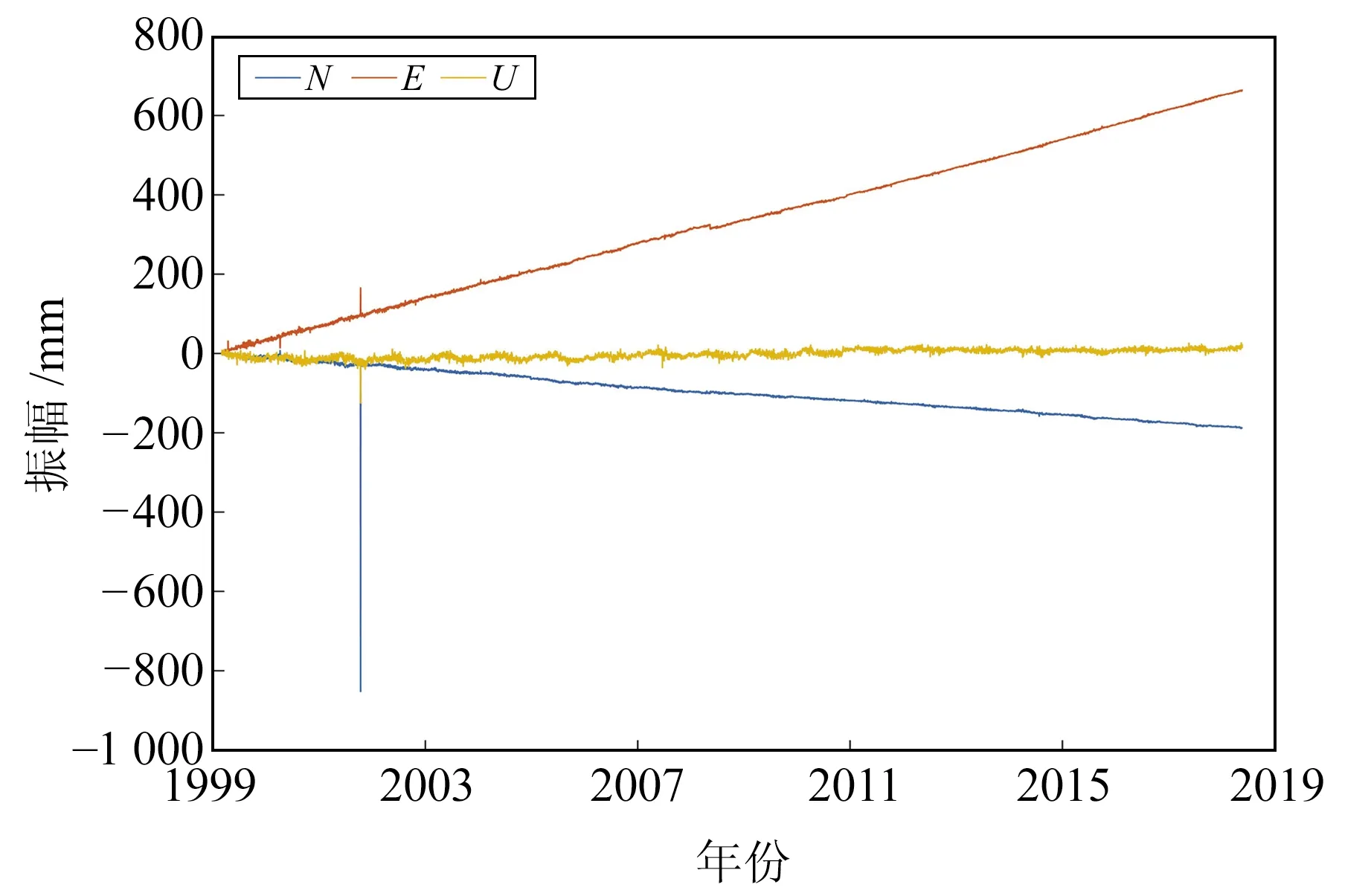
图7 LUZH站坐标时间序列Fig.7 The coordinate time series at LUZH station

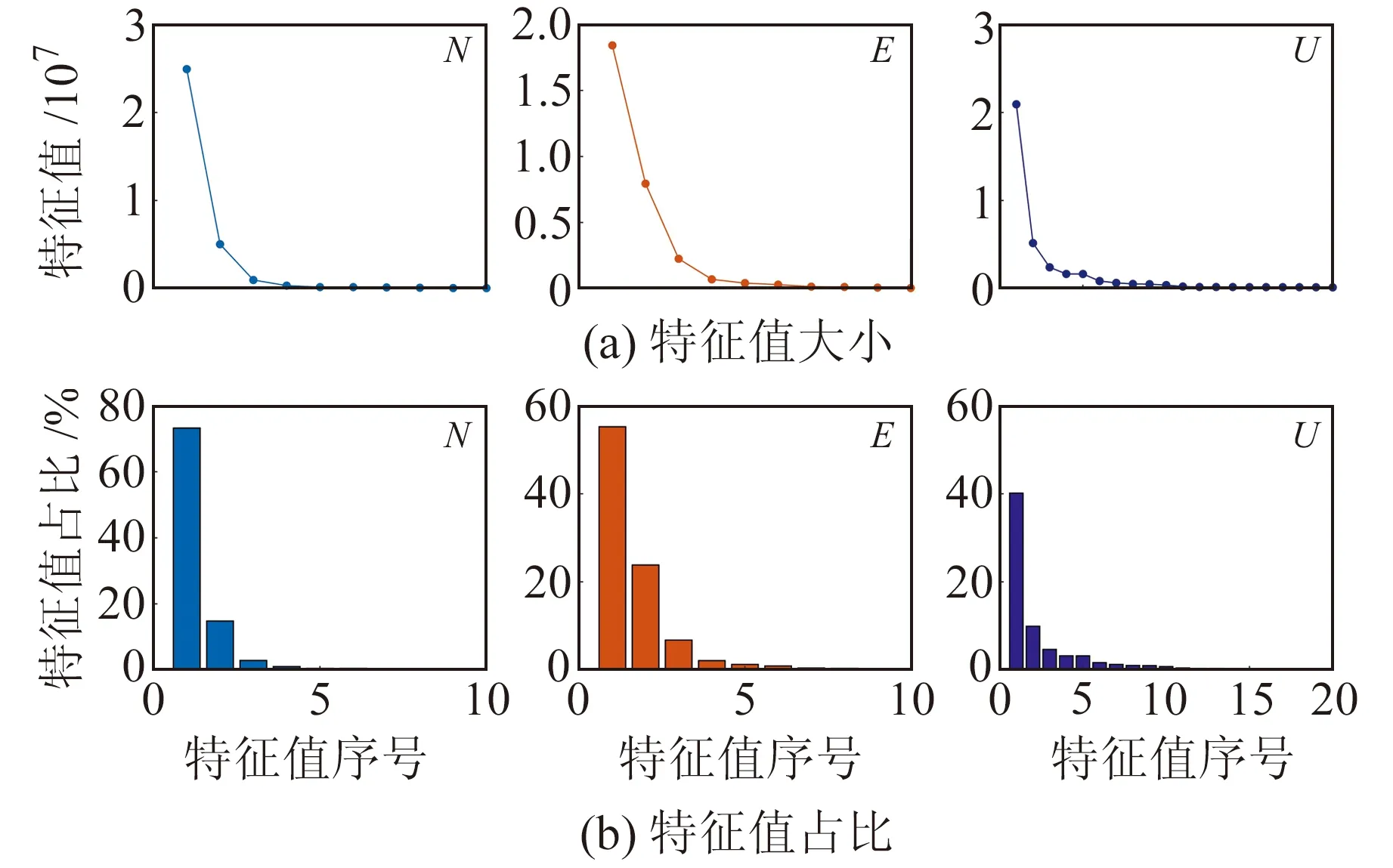
图8 轨迹矩阵协方差阵的特征值及其占总特征值之比Fig.8 The eigenvalues of the covariance matrixof the trajectory matrix and its ratio to the total eigenvalues

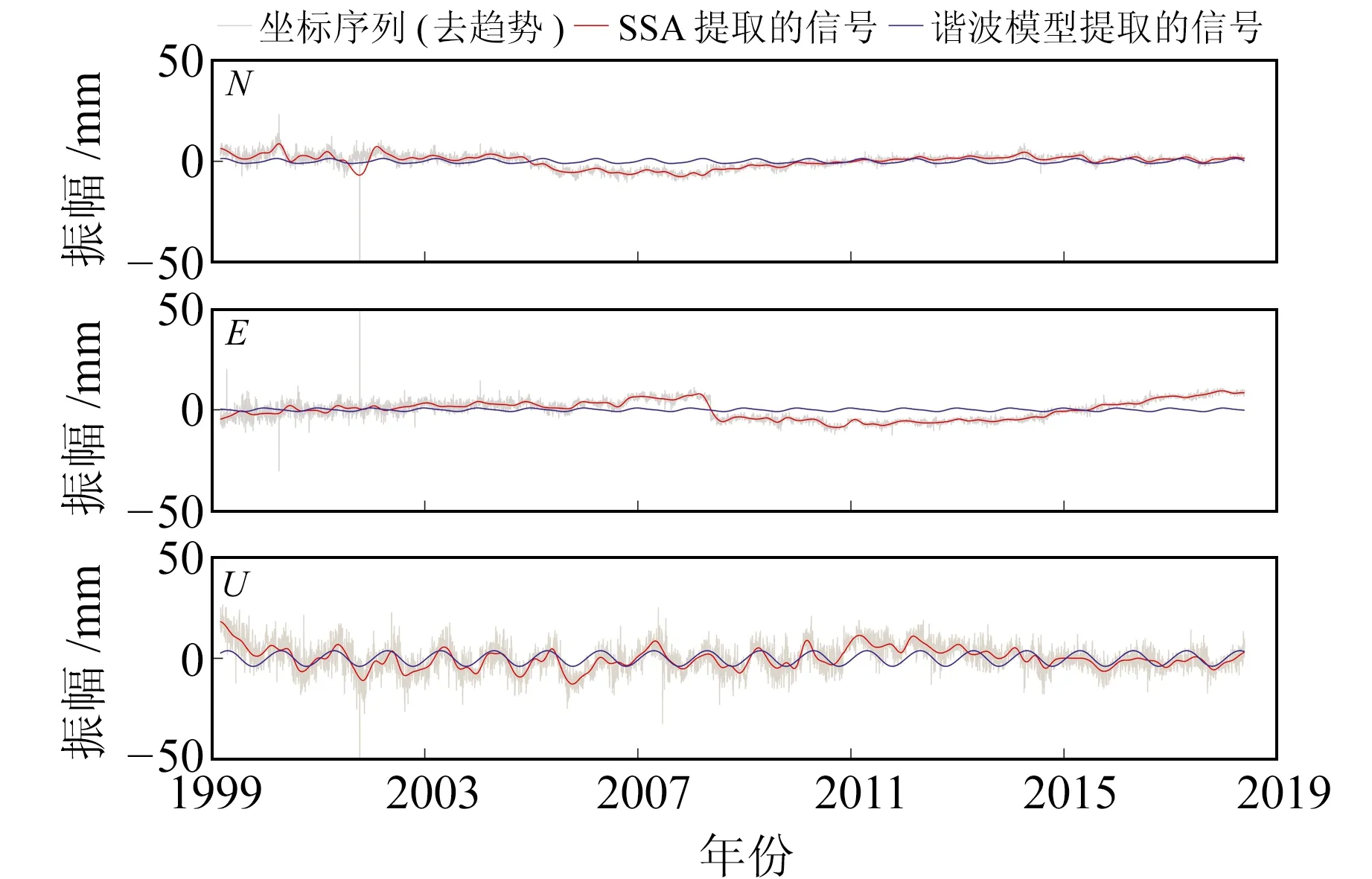
图9 LUZH站2种算法估计的信号Fig.9 Signals estimated by two algorithmsat LUZH station

将信号从原坐标序列中去除，分别采用本文算法和传统算法对残差序列进行粗差探测，图10为2种算法探测粗差剔除后的坐标序列。由图可见，采用本文算法处理后的坐标时间序列中几乎没有粗差，序列整体较为干净；而采用传统算法处理后的坐标时间序列仍存在一些小粗差(如1999～2003年)，这主要是因为谐波模型对该时段的拟合效果较差。分别采用2种算法估计坐标时间序列中的噪声分量，结果如表3所示。从结果来看，传统算法估计的噪声分量略大于本文算法。

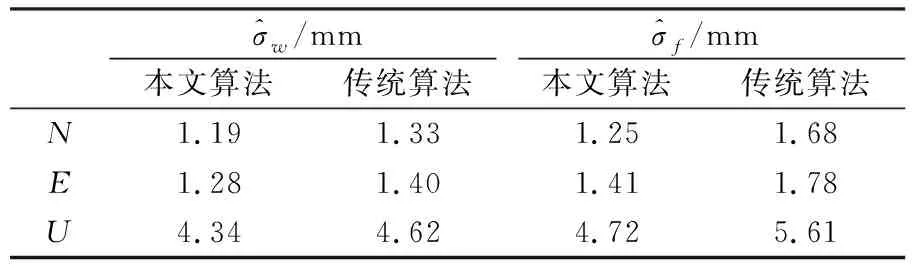
表3 LUZH站噪声分量估值

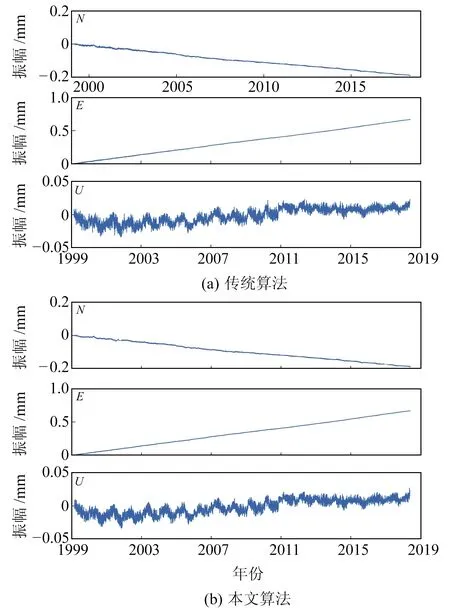
图10 2种算法探测剔除粗差后的坐标时间序列Fig.10 The coordinate time series after removinggross error by two algorithms

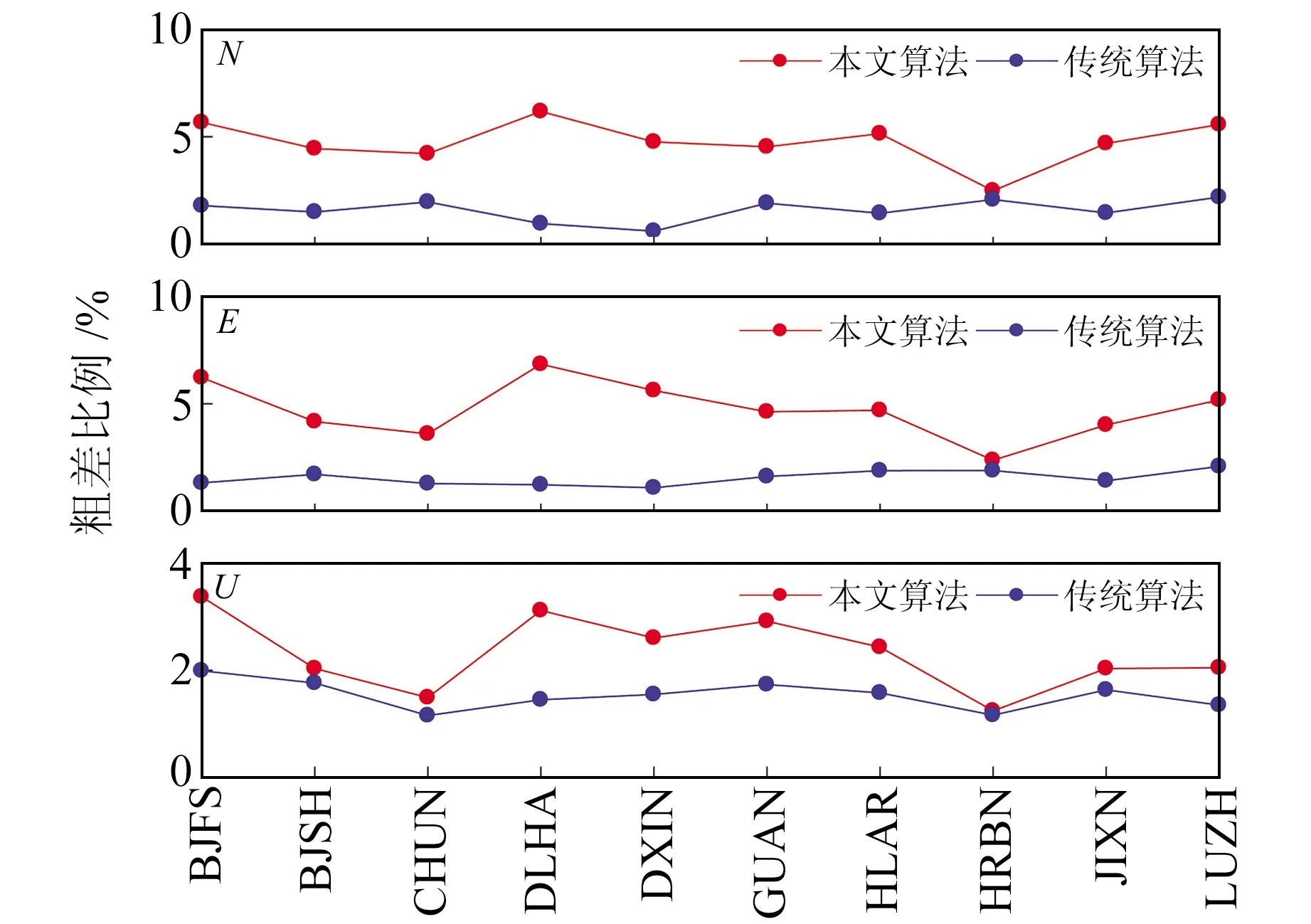
图11 2种算法探测到的粗差比例Fig.11 The proportions of gross error detected by two algorithms

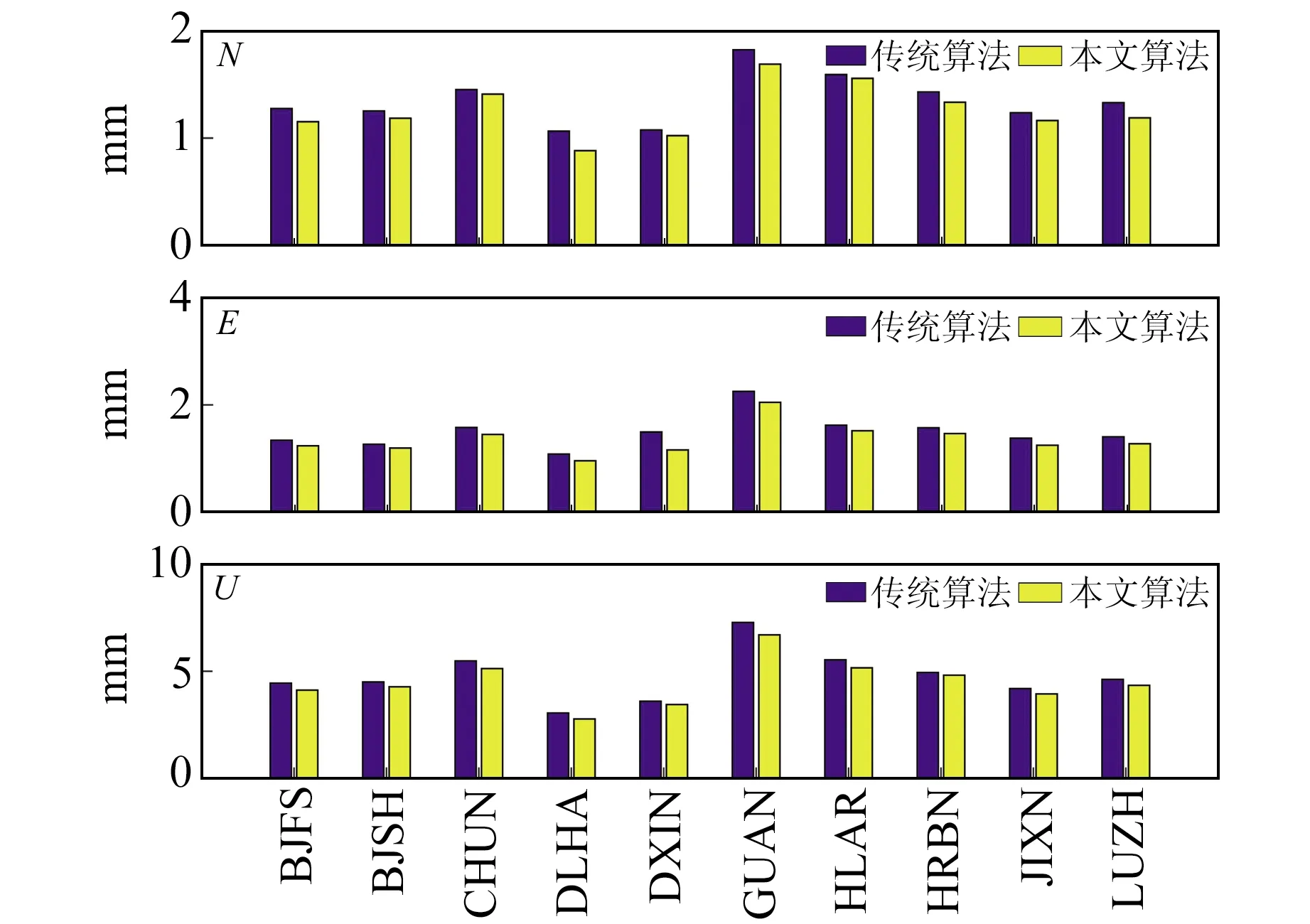
图12 2种算法估计的白噪声Fig.12 White noise estimated by two algorithms

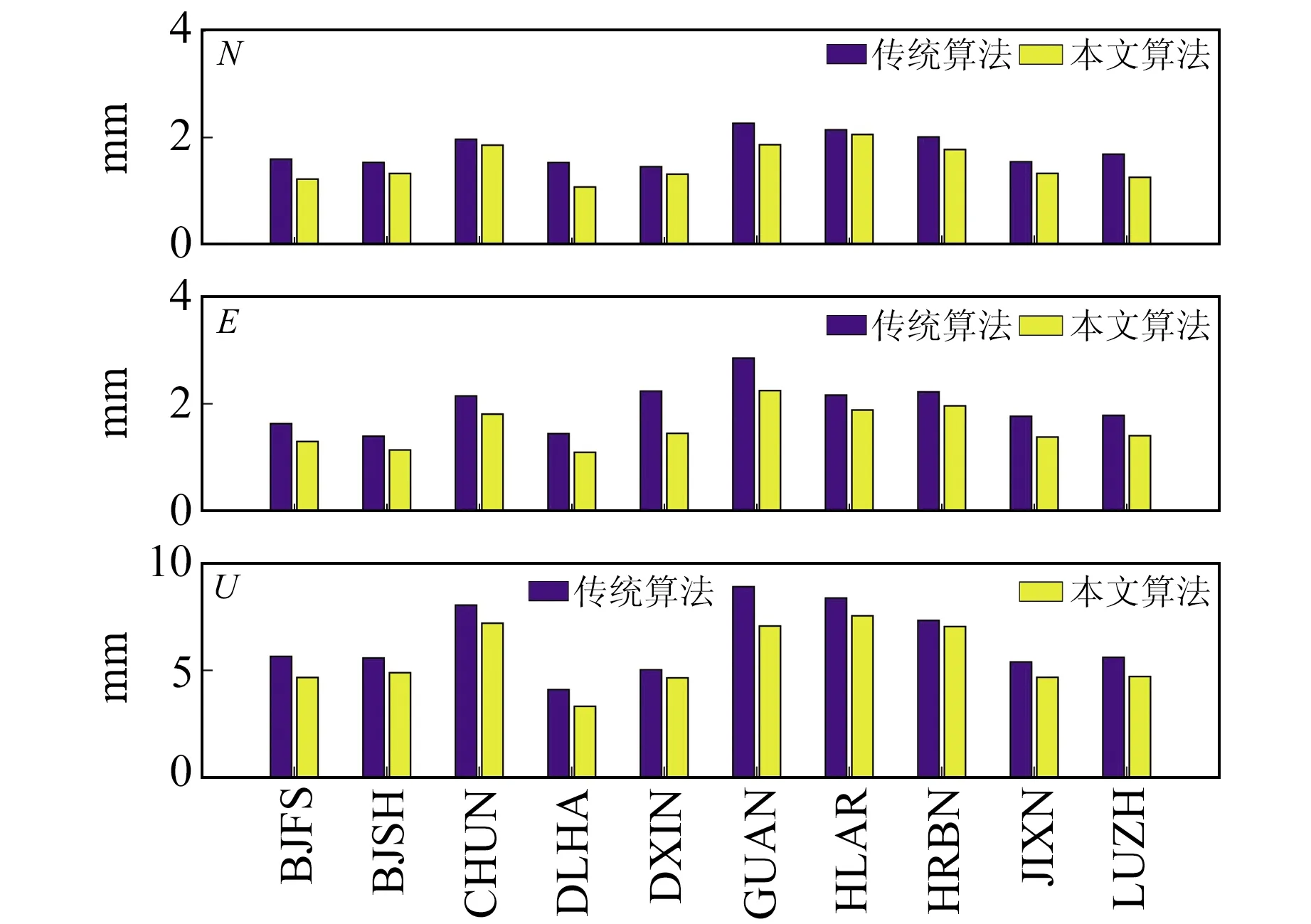
图13 2种算法估计的闪烁噪声Fig.13 Flicker noise estimated by two algorithms

4 结 语

由于多种因素的影响，GNSS坐标时间序列受到各类噪声和粗差的污染。为了能够更加精确地估计地壳形变信号，需将其中混有的粗差进行有效地识别、剔除并且对噪声进行准确的建模。以往进行粗差探测和噪声估计的算法大都是基于谐波模型进行构建的，然而谐波模型难以精确地描述GNSS坐标时间序列的非线性变化，进一步影响算法的性能。本文提出一种基于SSA的GNSS坐标时间序列粗差探测和噪声估计算法，并采用模拟实验对算法进行验证。实验结果表明，相比于传统算法，本文算法的粗差探测成功率更高，且估计的噪声分量与真值更为接近。陆态网络实测数据分析结果表明，高程方向时间序列噪声强度要高于水平方向，且闪烁噪声的振幅要高于白噪声。此外，由于谐波模型不正确的模型假设导致所获得的残差序列中仍含有部分信号，进一步导致其估计的噪声振幅略高于本文算法。