基于改进K-means聚类的配电网电压暂降频次估计法

李顺祎，汪颖，杨敏辉

(四川大学电气工程学院，四川 成都 610065)

0 引言

随着国民经济和高新制造技术的发展，电压暂降成为困扰现代制造业最为严重的电能质量问题之一[1—4]。典型电压敏感设备有计算机、变频器、交流调速器、交流接触器等[5]，这些设备对电压暂降的敏感特性主要取决于电压暂降的幅值和持续时间。电压暂降频次估计，即评估节点一年内发生的不同幅值和持续时间的电压暂降次数，其结果是评估敏感设备受电压暂降扰动程度的重要信息[6—9]，可为电压暂降的治理决策提供理论依据[10]。

在配电网电压暂降频次估计中，准确计算电压暂降幅值和持续时间十分重要[11—12]。电压暂降大多数情况由短路故障引起。国内外关于电压暂降频次估计的文献大都是针对电网中的短路故障，从线路故障率估计、电压暂降幅值估计和电压暂降持续时间估计几个方面进行深入分析。在暂降幅值估计方面，有相关文献考虑了故障阻抗[13—14]、系统运行方式[15]的影响。在电压暂降持续时间方面，近年来均是根据线路保护动作特性进行评估，研究了距离保护[16—17]、保护动作随机性[18]、反时限电流保护[19]、双端阶段式保护[20—23]等对暂降持续时间的影响。

可见，现有电压暂降频次估计方法都是单独针对电压暂降幅值或持续时间进行研究，具有一定缺陷。首先，现有方法较少考虑电压暂降幅值与持续时间之间的关联。事实上，电压暂降持续时间取决于线路保护的动作情况，而故障由哪段保护切除(文中称为保护动作段)由故障电流决定，故障电流大小直接决定了电压暂降幅值。因此，在电网某区域内，公共连接点(point of common coupling,PCC)的电压暂降幅值与持续时间之间必然存在一定映射关系，亟需对其进行挖掘探究，以获得可信度更高的电压暂降频次估计结果。

其次，配电网继电保护配置情况多种多样，针对不同区域、不同馈线、用户设置的保护整定值与动作时间都可能不同，不易详尽且完整地获取整个电网各线路的保护配置情况。再次，传统方法认为固定范围内的故障将由固定的保护段切除。事实上，随着故障阻抗、故障类型和运行方式的不同，保护的范围变化较大[24—25]。同一位置的故障，在不同的情况下其持续时间可能不同，这就造成了电压暂降持续时间估计的误差。

针对现有方法对保护动作判断不准确和保护配置获取困难的现象，提出一种基于改进K-means聚类算法的配电网电压暂降频次估计法。根据电压暂降幅值影响因素和配电网保护动作特性，分析电压暂降幅值与持续时间的映射关系，提出可根据电压暂降幅值来判定保护动作情况。无需获取保护配置信息，基于电压暂降历史监测数据与保护动作信息，采用改进K-means聚类算法推断线路保护配置情况，计算保护动作时间和保护动作电压，在考虑不同故障类型、不同运行方式及不同过渡阻抗的情况下进行配电网电压暂降频次估计。在IEEE RBTS-6母线测试系统的母线5配电网中进行了仿真，验证了文中方法的有效性和正确性。

1 电压暂降特征量计算

1.1 电压幅值

电压暂降幅值指发生电压暂降时节点的残余电压，其大小取决于故障电流、网络拓扑、运行方式、故障类型、故障位置与过渡电阻等因素。电网短路计算模型如图1所示。

图1 电网短路计算模型Fig.1 Short circuit calculation model of power grid

以线路ij上发生三相短路f为例，设f点距离线路首端i的距离标幺值为l，则f点距线路末端j的距离为1-l，Rf为故障过渡电阻。在考虑不同运行方式和短路过渡电阻的影响下，被评估节点m(PCC)的电压暂降幅值公式为：

(1)

(2)

式中：Zim，Zjm分别为线路首端节点i、线路末端节点j和被评估节点m之间的互阻抗；Zii，Zjj分别为节点i和j的自阻抗；Zij为节点i，j的互阻抗；zij为线路ij的单位长度阻抗。若故障为不对称短路，则需利用对称分量法，将各序阻抗代入式(2)，求出故障点各序自阻抗与互阻抗，再进行电压暂降幅值计算。由于篇幅受限，具体计算公式见文献[26]。

1.2 持续时间

故障导致的电压暂降持续时间通常根据保护配置和整定情况进行评估。配电网为实现安全、可靠、经济性运行，通常采用阶段式继电保护作为主保护，如电流保护、零序保护和距离保护等[27—29]。阶段式保护的整定中，每段保护的动作电流或阻抗设置为不同的整定值，并且在动作时间上设置一定级差，以保障保护的灵敏度和选择性。现有环型配电网在绝大多数情况下通常为开环运行，仅在故障发生后转移供电时，联络开关会暂时闭合。因此，配电网中的继电保护配合情况可按照辐射型网络进行分析。以单端电源配电网为例，节点A，B，C出口断路器均配置了三段式电流保护，设保护Ⅰ段、Ⅱ段、Ⅲ段的动作时间分别为t1，t2和t3，在最大运行方式、无过渡电阻的三相短路情况下各级保护范围和动作时间如图2所示。

图2 单端电源配电网中的三段式电流保护Fig.2 Three-stage current protection in single ended power distribution network

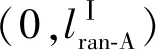
2 基于保护动作电压的暂降持续时间评估

2.1 传统基于保护动作特性方法的不足

在配电网中，不同馈线上的保护动作值是根据负荷类型、容量、线路阻抗等参数整定的，不同线路上保护的整定值可能不同，那么各级保护的保护范围也不尽相同。此外，随着故障类型、故障阻抗和运行方式的改变，短路电流的大小将受到显著影响，即使是在同一位置处发生的故障，其短路电流也可能千差万别。因此，各级保护的灵敏度，即有效动作范围应是不断变化的。若按照传统基于保护动作特性的方法[16—17]，认为各条线路上各级保护的范围相同且固定不变的话，势必给电压暂降持续时间的估计带来偏差。

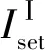
图3 不同Zf下的故障电流曲线Fig.3 The fault current curves under different Zf

2.2 电压暂降幅值与保护动作段的关系

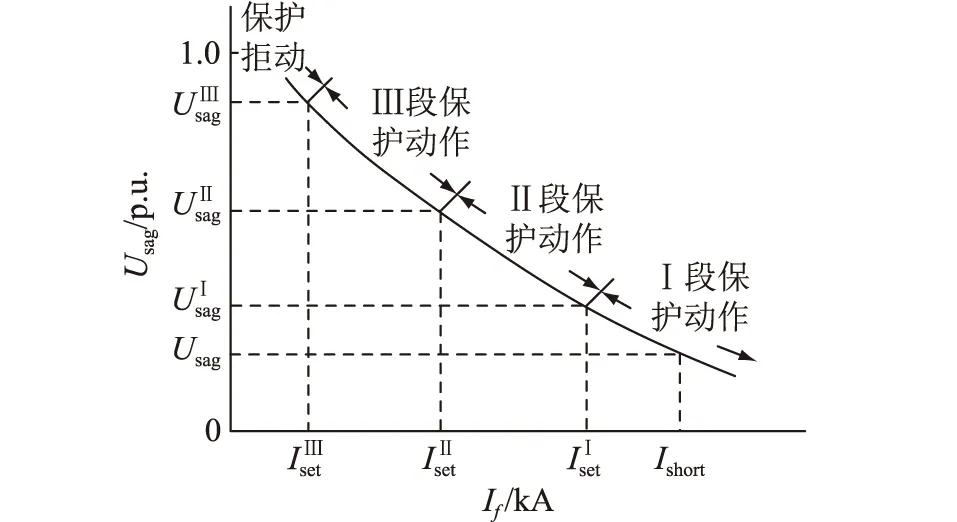
图4 PCC电压暂降幅值与故障电流的关系曲线Fig.4 The relationship curve between the voltage sag and fault current at PCC

在配电网中的辐射型网络或者开环运行网络中，通过对大量历史电压暂降幅值-持续时间进行聚类分析，可以得到PCC电压暂降幅值与保护动作段之间的规律。基于得到的规律进行配电网电压暂降频次估计，将大幅提高电压暂降持续时间特征估计的准确性。

2.3 不同Zf下的电压暂降持续时间评估

电网中发生短路故障时，引起PCC的电压暂降幅值Usag与故障点在线路中离首端距离l的关系可由电压暂降幅值曲线表示，PCC电压暂降幅值曲线如图5所示。在双侧电源的环网中，该曲线一般呈现为非单调的凸函数；而在辐射型网络中，该曲线为一条单调递增的曲线。

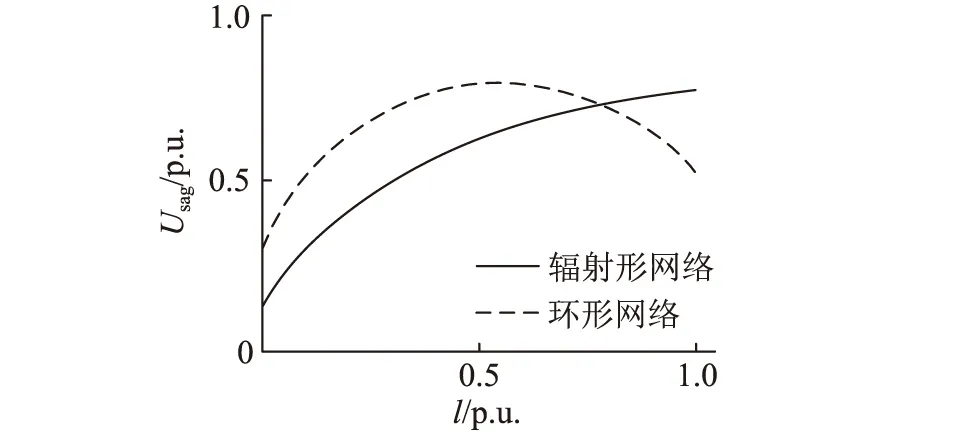
图5 PCC电压暂降幅值曲线Fig.5 Voltage sag curves at PCC

考虑在不同Zf下，结合图4中分析的电压暂降幅值与保护动作的关系，绘制三相短路时的PCC电压暂降幅值曲线，如图6所示。

图6 三相短路下不同Zf的电压暂降幅值曲线Fig.6 Voltage sag curves of different Zf under three phase short circuit

可见，根据电压暂降幅值曲线能够清晰地判定线路不同位置发生故障时所对应的保护动作段。比如，Zf为0 Ω和2 Ω时，保护Ⅰ段分别能够切除线路60%和40%范围内的故障，暂降持续时间为t1，剩下部分的故障由保护Ⅱ段切除，暂降持续时间t2。以上规律可由式(3)表示：

(3)

同时也可从图6看出，在不同Zf下，电压暂降幅值存在较大差异，继电保护动作情况也有所不同，同一个位置发生的故障，使保护Ⅰ段、Ⅱ段、Ⅲ段动作或拒动的情况均可能发生。在最大运行方式和金属性短路的情况下(Zf=0 Ω)，保护Ⅰ段有效保护区最大，随着运行方式或过渡电阻的改变(即Zf增加)，保护Ⅰ段的保护范围逐渐减小，在Zf>5 Ω时，保护Ⅰ段无保护范围；当Zf>50 Ω时，保护Ⅱ段也无保护范围，故障仅由后备保护，即保护Ⅲ段切除；当Zf继续增大时，甚至会出现后备保护也无有效范围的情况，导致保护拒动，当然在此种情况下，短路电流已较小，引起的电压暂降幅值(残余电压)也比较高。因此，应根据不同的故障类型、不同运行方式和不同过渡电阻，计算线路的电压暂降幅值曲线，结合保护动作电压判断其触发的保护动作段，从而确定对应的电压暂降持续时间。

3 基于暂降监测数据的保护动作电压计算

在配电网保护的整定值和保护范围未知的情况下，基于历史电压暂降监测数据，分析电压暂降幅值与持续时间的关系，通过聚类算法获取保护动作段随暂降幅值变化的规律，得到不同故障类型、不同运行方式和不同过渡电阻下的各级保护有效动作范围，从而评估各故障点导致的相应暂降持续时间，最后根据结果进行配电网电压暂降频次估计。

3.1 提取历史电压暂降特征量

(1)电压幅值。基于电压暂降采样数据，采取IEC 61000-4-30推荐算法，通过计算电压有效值得到电压暂降幅值：

(4)

式中：s为采样点序号；S为采样点数。

(2)持续时间。据IEC 61000-4-30中对电压暂降的定义，电压暂降持续时间以电压幅值低于90%额定电压所持续的时间计算，即：

(5)

式中：fs为采样频率；Ur为额定电压。

3.2 基于改进K-means聚类的线路保护动作段识别

配电网具有馈线数量多、负荷种类复杂的特点，针对不同线路、负荷的继电保护配置方案可能不同，因此不同PCC处的电压暂降持续时间多样。可根据实际的电压暂降监测数据，判定馈线配置的保护级数、动作时间以及相应的继电保护幅值区间。文中采用改进K-means聚类算法，对基于电压暂降监测信息计算的电压幅值和持续时间数据进行二维聚类，得到各保护阶段内对应的电压暂降幅值-持续时间的聚类中心与边界。

3.2.1 改进K-means聚类算法

K-means聚类算法[30—32]采用欧氏距离作为相似性测度，并以误差平方和为聚类准则。传统的K-means算法在聚类开始前需指定类别数目k，然而，在继电保护配置未知的情况下，无法事先确定线路安装了几段保护。因此，需对K-means聚类算法进行改进，使其自动判别最优聚类数目k。由于配电网线路故障的保护动作段可包括保护Ⅰ段动作、保护Ⅱ段动作、保护Ⅲ段动作和保护拒动，因此持续时间应分别集中在t1，t2，t3的附近，并可能包含极少数远大于t3的值。

改进后的K-means算法步骤如下：

(1)初始化类别数目k和初始聚类中心点，类别数目k初始值取为1。

(2)计算K个样本和k个初始中心点的距离，按照距离大小进行类划分，形成k个聚类。

(3)计算每类中所有对象的平均值，作为k个类别的新聚类中心。

(4)利用式(6)判断是否收敛。若ε未达到收敛阈值，则重复步骤(2)和步骤(3)；若ε小于收敛阈值，表明算法收敛，该次聚类结束。

(6)

式中：Ek为第k个聚类的所有样本集合；Yy为Ek中的样本；ek为Ek的聚类中心。

(5)根据式(7)计算轮廓系数Ck，评价本次聚类效果。单个样本y的轮廓系数计算方法如下：

(7)

式中：p1(y)为点y到所属类别中其他点的平均距离；p2(y)为点y到非所属类别中所有点平均距离的最小值。计算所有样本轮廓系数平均值，则可得本次聚类结果的轮廓系数Ck，即：

(8)

(6)取类别数目k=k+1，重复执行上述步骤，直到k大于3时，整个聚类算法结束。

(7)取各次聚类结果中使轮廓系数最大的k值，并将该次聚类结果作为最终的聚类结果。

3.2.2 保护动作段与动作时间判定

根据电压暂降持续时间聚类结果，可获取线路继电保护配置级数以及整定动作时间。其中，聚类类别数目k即为保护安装级数，每类别的时间维度的聚类中心即为各级整定动作时间。假设各类别聚类中心为(Ue1,de1),…,(Uek,dek)，当k=1时，馈线仅安装了过电流保护；k=2时，线路安装二段式保护；k=3时，线路安装了三段式保护。各级保护整定的动作时间分别为de1,…,dek。

3.2.3 各级保护动作电压的计算

文中采取计算边界均值的方法判定电压暂降幅值边界。为获取保护k段电压暂降幅值，分别找到类别k中电压暂降幅值最大值Uk_max和类别k+1中的电压暂降幅值最小值Uk+1_min，取两者的平均值作为保护k段电压暂降幅值Uk_sag，即：

(9)

3.3 基于保护动作电压的配网电压暂降频次估计

按照3.1节和3.2节的方法计算得到配电网线路的保护动作级数、动作时间和动作电压幅值后，利用故障点法进行配电网电压暂降频次估计，即依次确定每个故障点导致的电压暂降幅值和持续时间。对于某条线路，在各个位置处发生故障所造成的电压暂降幅值和对应的持续时间应按照第2章的方法，即根据不同故障类型、不同运行方式、不同过渡阻抗绘制多条电压暂降幅值曲线，并结合保护动作电压进行判断。

文中针对变化多样的运行方式和过渡电阻值，结合实际运行情况和工程应用，选取Zf=[0,100]范围内的Nz组数值。因此，各线路发生故障，被评估的PCC电压暂降频次为：

(10)

式中：β为故障类型；M1为该线路上符合Usag约束条件的故障点数量；M2为线路设置的故障点数量；δβ为该线路发生相应故障类型的故障率；z为Zf的序号；Nz为Zf值选取的个数；Umin,Umax分别为电压暂降频次表中对应电压幅值区间的下界和上界；dmin,dmax分别为电压暂降频次表中对应持续时间区间的下界和上界。电压暂降幅值Usag由式(1)计算，持续时间dsag由计算的Usag和保护动作电压、保护动作段确定。由于文中提出的方法仅针对线路发生的故障，因此暂不考虑母线发生故障导致的电压暂降。

2017年6月26日，苏州某地铁线路部分列车在ATO模式下，出现司机界面显示时间不正确，以及在站台停站时间过短的现象。

文中所提电压暂降频次估计流程如图7所示。

图7 电压暂降频次估计流程Fig.7 Voltage sag frequency estimation process

4 仿真分析

4.1 仿真网络参数

为了验证文中所提频次估计方法的有效性与准确性，应用RBTS-6母线测试系统[33]中母线5下的部分配电网络进行仿真实验，如图8所示。配电站母线有2条主馈线出线，每条馈线下有若干条支线，设主馈线和支线上各种类型的故障率如表1所示。设出线断路器1及出线断路器2均配置了对应相间故障的三段式电流保护和对应接地故障的三段式零序保护，为了方便计算，设电流保护和零序保护的整定值相同，各保护整定电流值与动作时间如表2所示。馈线上配置的若干分段器无切除故障电流功能，仅用于隔离永久性故障。馈线1、馈线2的长度分别为15 km和20 km，每条支线长度均为5 km，馈线联络开关断开，网络开环运行。出线断路器均配备一次重合闸功能。重合闸重合于永久性故障时，会导致2次连续的电压暂降事件，而第二次暂降事件一般不会对敏感设备造成二次影响。因为如果第一次设备未跳闸，第二次暂降也不会导致设备跳闸。因此，在短时间内由于重合闸导致的2次电压暂降一般仅作为一次处理[34]。

图8 RBTS测试系统母线5配电网Fig.8 RBTS test system bus 5 distribution network

表1 线路各类型故障率Table 1 Failure rate of various types of lines

表2 各级保护整定值及动作时间Table 2 Setting value and action time of protection at each stage

需注意，文中方法的提出是建立在未知保护整定参数的基础之上，利用历史监测数据判定保护动作规律，进而进行电压暂降频次估计，因此算法中无需获取表2参数。表2中设定的保护整定参数是用于产生算法所需的电压暂降历史监测数据的，同时也可以验证本算法计算保护动作值的准确性。

4.2 产生电压暂降样本数据

(1)产生短路故障。文中应用蒙特卡洛法，在图8所示的配电网中随机产生1 000次故障。其中，故障类型根据表2所示故障类型比例随机选择；故障在线路中的位置服从U(0,1)的均匀分布；Zf的取值为0 Ω,5 Ω,10 Ω,…,50 Ω，并从这11组值中随机均匀选取。

(2)计算电压暂降幅值与持续时间。根据1.1节中的公式计算各次故障导致配电站母线的电压暂降幅值和故障电流If；对于电压暂降持续时间，首先基于If的大小，按照表1中电流整定值判定保护动作段，且为了模拟实际情况中如保护操作机构、数据计算误差等各种因素对电压暂降持续时间的影响，在保护动作时间上随机加一服从正态分布的数值xt～N(0,5)作为对应保护动作段的电压暂降持续时间。

4.3 计算保护动作段及保护动作电压

基于所提算法，并根据断路器动作信息(故障由断路器1或断路器2切除)对电压暂降幅值-持续时间数据进行聚类。聚类前的电压暂降幅值-持续时间散点图如图9(a)所示，基于改进K-means聚类算法的聚类结果如图9(b)所示。为对比改进后的效果，将算法改进前固定k=2,4进行聚类，聚类结果如图9(c)、图9(d)所示。

由图9(b)可见，对于2台断路器对应出线发生的电压暂降，聚类算法均自动将其分成了3类，与仿真设置的三段式保护相符，各类别的聚类中心如表3所示，计算各断路器的各级保护动作电压如表4所示，聚类时间维度上各类别聚类中心的de与设置的继电保护动作时间整定值基本一致，各级保护动作电压能够在电压幅值维度上把不同类别的电压暂降区分开。而由图9(c)可见，取k=2时将保护Ⅱ段和保护Ⅲ段切除的故障聚成了一类，其聚类中心无法反映出各级保护的动作时间和动作电压。取k=4时，同一级保护切除的样本数据被聚成了2类，与实际不符。不同线路保护的动作级数可能不同，改进前的算法仅当k取值恰好为保护动作级数时，才能获得正确聚类结果。改进算法后，能够自动选取适合的k值，使算法适应不同的保护配置。

表3 各类别聚类中心Table 3 Cluster centers of each category

表4 各级保护动作电压计算结果Table 4 Calculation results of protective operating vltage of each stage p.u.

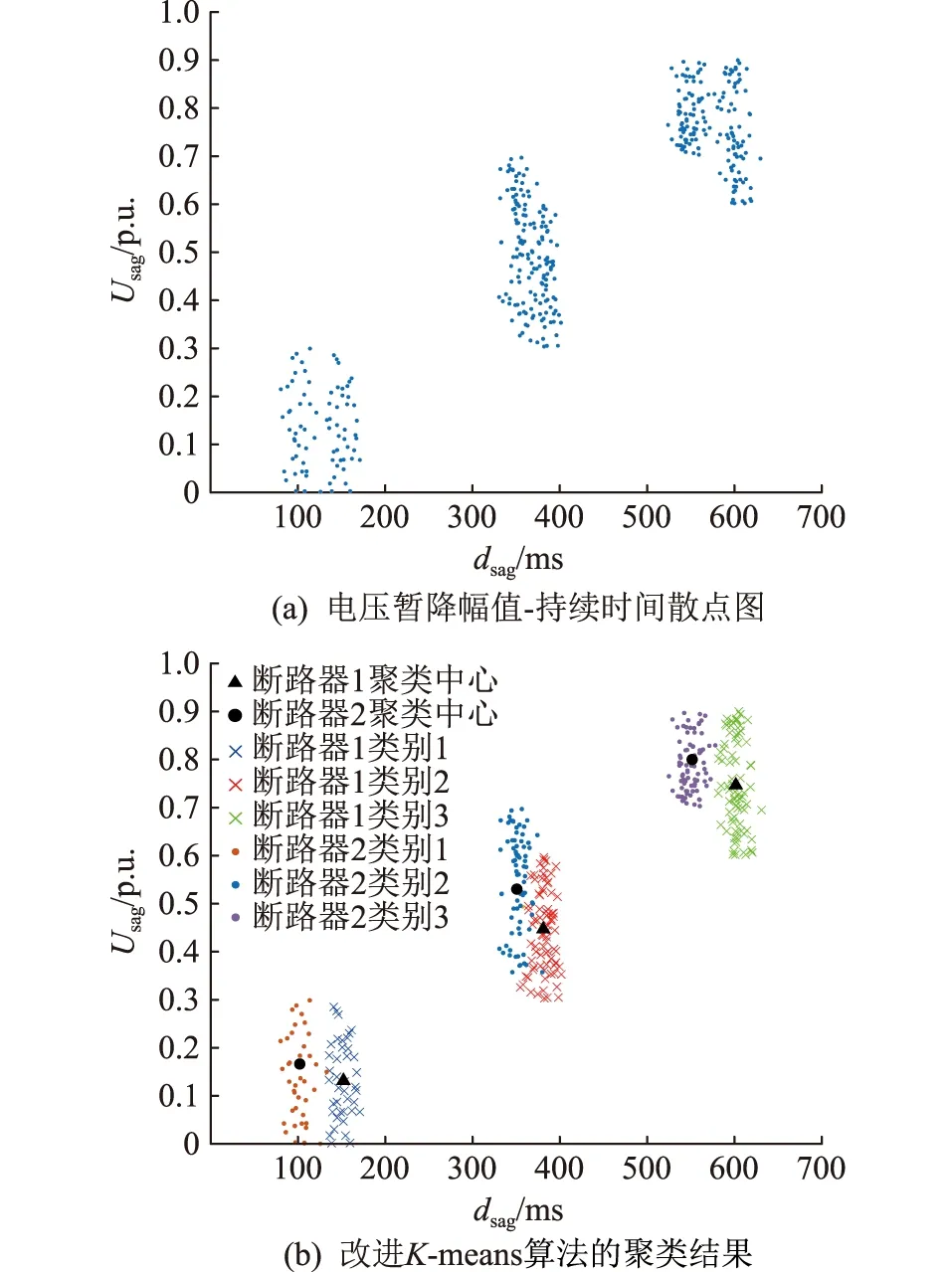
图9 电压暂降样本数据散点图与聚类结果Fig.9 Scatter plot and clustering results of voltage sag monitoring data

4.4 电压暂降频次估计

基于4.3节计算的保护动作电压和保护动作时间，采用故障点法，按照表2的故障率进行配电网电压暂降频次估计。传统考虑保护动作特性的电压暂降频次估计法[14]认为馈线固定长度内发生的故障由固定保护段切除，且不考虑运行方式和过渡阻抗对继电保护动作的影响，将其与文中方法进行对比，评估结果见表5和表6。其中，表5为暂降幅值频次估计结果，表6为持续时间频次估计结果。将2种评估方法的结果与真实电压暂降频次(基于样本归一化后的频次)进行对比，并计算相应误差。

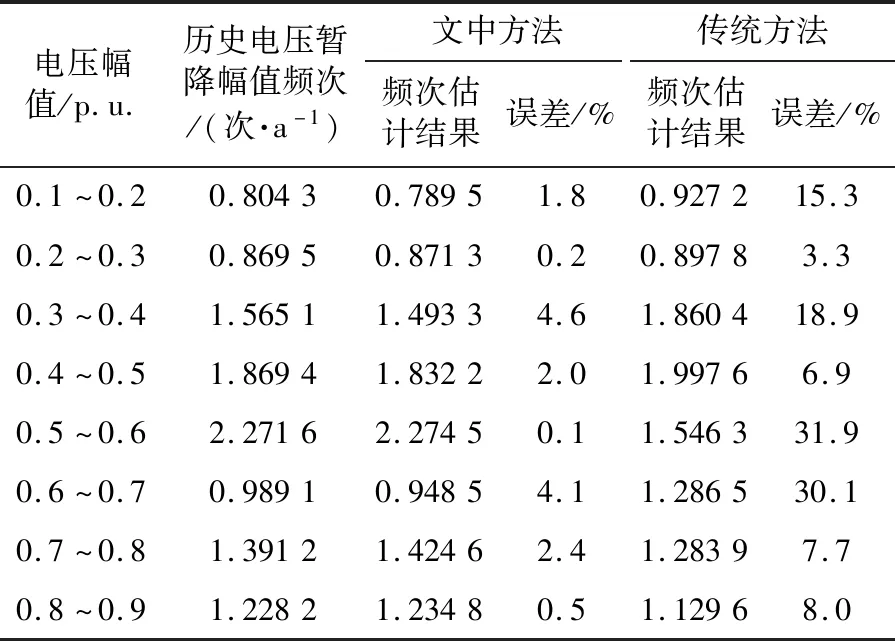
表5 电压暂降幅值频次估计结果Table 5 Estimation results of voltage sag amplitude frequency

表6 电压暂降持续时间频次估计结果Table 6 Estimation results of voltage sag duration frequency

由表5和表6可知，文中方法在暂降幅值与持续时间的频次估计上均比传统方法更接近于实际暂降频次。其中，文中方法和传统方法在电压暂降幅值频次估计的平均误差分别为2.0%和15.3%，这是由于考虑了运行方式和过渡阻抗影响。在持续时间频次估计中，文中方法和传统方法平均误差分别为1.1%和20.7%，说明传统方法仅以线路固定长度范围为依据来判断保护动作与暂降持续时间带来的误差较大，而文中方法根据比较电压暂降幅值与保护动作电压来判定保护动作段，从而确定暂降持续时间，使评估结果的误差大幅减小。

准确的电压暂降频次评估结果对敏感用户生产意义重大。首先，明确电压暂降频次，有利于用户评估在该节点建厂的风险，从而筛选出电压暂降相对浅和持续时间相对短的节点，以减少电压暂降导致工业停产损失的频次；第二，准确的电压暂降幅值和持续时间是评估敏感用户工业过程受电压暂降影响程度、经济损失等指标的基础，也是用户选择治理设备的容量选型的依据；第三，对于某些敏感设备，通过分析暂降数据获取保护动作时间和动作电压，并根据设备耐受能力调整保护定值，可缓解敏感设备跳停问题。

5 结论

文中提出了一种基于改进K-means聚类算法的配电网电压暂降频次估计方法。针对K-means聚类算法在未知类别数时聚类效果差的缺陷，引入轮廓系数使其自适应确定最优聚类数，从而达到识别线路保护动作段的目的。基于最优聚类结果，计算保护动作引起的电压暂降持续时间，从而得到节点电压暂降频次估计结果。得到以下结论：

(1)文中所提方法有效解决了配电网电压暂降频次估计中线路保护配置获取困难的缺陷。在未知线路继电保护配置的情况下，与传统假设保护方案的方法相比，文中方法能在暂降持续时间上获得更接近于实际情况的评估结果。

(2)文中方法进行了不同运行方式和过渡阻抗下的电压暂降频次估计，利用各级保护动作电压，有效地判断继电保护的动作情况，避免了传统方法判断保护动作错误的问题，提升了电压暂降持续时间准确性，使频次估计结果较传统方法更具可信度。

(3)文中仅针对电网节点挖掘电压暂降幅值与持续时间之间的关系，以评估节点电压暂降频次。若要考虑暂降对工业过程的影响，还需结合设备耐受曲线、过程免疫时间等进行评估。

(4)文中所提方法仅针对辐射型网络或开环运行的配电网络，根据电压暂降检测数据计算和推断闭环运行的环形网络保护配置情况方面的方法还有待深入研究。