借比较之力，实施结构化教学——以《笔算两位数乘两位数(不进位)》教学为例

吴丽丹

(福建省厦门市集美区高浦小学 福建 厦门 361021)

洛德·列维斯特劳斯指出人类一切活动都有内在组织结构普遍被认为存在于人类的活动中，它能使看似分离的文化有一体的形态。学生在学习新知识的过程中普遍存在结构护额的特点，学习的过程不是单一的接受过程，而是在沟通已有认知和新知之间的关系。因此我们在教学课程内容时，便要思考课程的编排意图，本节课知识处于整个计算课堂的什么位置，与前面知识之间存在什么样的联系，又为接下来的学习提供多少铺垫，教什么？教多少？笔者从以下几个方面，在本节课中，促进结构成型。

1.在具体情境中比较，促使方法结构化

方法结构是指学习知识的过程中出现类似或者相同的结构。在教学时应当主动帮助学生感知方法结构，可以利用已有的解决问题的方法来解决面对的新问题，知识是人们基于经验而被创造出来的。在教学时选取学生熟悉的、有感情的情境，让学生感受问题产生的必要。设置串联式的具体情境，不仅有连贯性，也能让学生置身其中。对不同情境的比较，帮助学生回忆已有的知识方法，促进学生进行知识之间的串联及转化。

例如：在教授两位数乘两位数时，笔者设置要为班级图书角增添新书，让学生为班级解决问题，先是出示2套书，学生感受到只买2套书数量太少了，不够。再出示6套书，接着出示10套书，最后出示12套书，分别让学生计算出总的有多少本，再让学生进行比较，提出问题：“为什么都是用乘法计算，你有的题目能算出来，有些题目不会计算呢？”引导学生对两位数乘一位数及两位数乘整十数的计算进行回忆。再通过提问：你是怎样计算两位数乘一位数及两位数乘整十数的？引出计算的方法“先分后合”。学生既回忆计算的方法，又沟通了两位数乘一位数和两位数乘整时数在方法上的联系。紧接着让学生估一估14乘12的值可能是多少，在点子图上指一指估算的范围，通过不同的估算方法，指出的范围，为学生接着利用点子图来分一分提供了思路及方法，帮助学生熟悉点子图。学生出示以下几种估算方法：

进一步结合具体情境进行比较，图1是将12套书估成10套，算的是10套书的本数；图2是将一套书估成10本，这时候12套书有120本。图3是将每套书的本数看成10本，买了10套书。通过在具体情境中的比较，学生能够掌握估算的道理，虽然估的方式不同，但是估的方法都是将乘数估成了整十数，为接下来的分一分、算一算作铺垫，估算的过程实际上也是在“分”，把12套书分成10套和2套、把14本书分成10本和4本，两种估法之间是存在共同点的。通过具体情境中的分析和比较，促使学生感知方法结构化。

图1 图2 图3

2.在新知教授中比较，促进思维结构化

结构化思维是一个层次分明的、逻辑清晰的思考问题的路径，如果学生在进行学习时，能够逐渐形成结构化思维，将能化零散为一体，化无序为有序，思考问题更有条理性、逻辑性。笔者认为，在课上可以通过分类、比较、有意识的排序、鼓励关联等方式，促进思维结构化。

例如：大胆放手让学生利用点子图分一分、圈一圈、写一写，算出12乘14的结果。学生出示几种做法：

14×6=84(本) 14×3=42(本) 14×9=126(本) 14×2=28(本)

84×2=168(本) 42×4=168(本) 14×3=42(本) 14×10=140(本)

126+42=168(本) 140+28=168(本)

① ② ③ ④

引导学生进行分类后发现，方法①、②是把12套书平均分成若干份，方法③、④是将12套书分成两份，没有平均分。再通过对比后发现，它们能求出12套书的本质都是在“先分后合”只不过分的方式不一样。再从中优化出分成整十数和一位数时是最具有普遍性的做法。学生会产生这么多种的计算方法，得益于前面一节课所学习的一位数乘整十数中，学生用了多种方式解释6×10为什么等于60这个问题，同时分类和对比更有利于思维结构化的发生，能使潜在的联系变得更显而易见。

在通过“先分后合”求出12x14的结果后，笔者没有加以过多地“扶”，而是放手让学生尝试大胆地用笔算表示出计算过程，从学生呈现出来的结果来看，学生能够对今天所要解决的新知识和已有的知识结构进行串联，并能尝试呈现出来，有如图4几种做法：

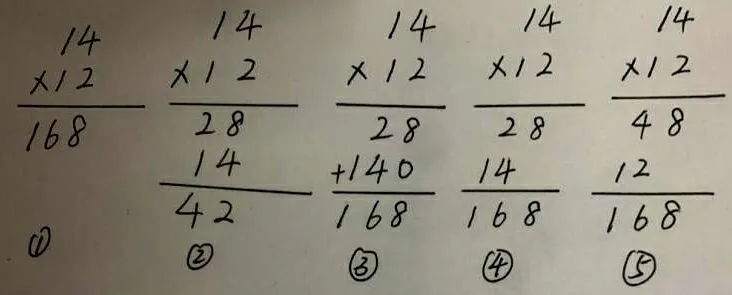
图4

教师有计划地呈现这些素材：先呈现①，发现没有过程，再呈现②、③进行对比，理解12的正确位置；再对比③、④，明确在第二层写120和写12，只要1在百位，2在十位上，表示的数的大小相同；进行到这里，学生已初步形成两位数乘两位数笔算的算法，紧接着引导学生比较刚才的分步计算和现在的笔算，有没有什么异同点。学生板书如图5，学生通过比较笔算和分步口算的方法，将二者进行关联，明白笔算的过程也是在先分后合，不仅理解了笔算的算理，学习到了知识的本质，还实现了思维上的结构化。在学生充分理解算法和算理的基础上，再呈现⑤，观察对比后发现，实际上它也是在先分后合，只是分的数不同。学生在新知教授的过程中，经历了思维结构化的过程，帮助学生能够有序地调动已有的经验来解决问题。

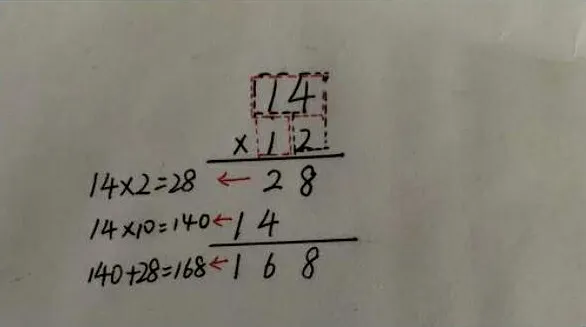
图5

3.在巩固提升中比较，帮助知识结构化

布鲁纳曾研究知识结构在整个课程中的重要意义。不论我们选择什么学科，务必使学生理解该学科的基本结构。学生不仅要掌握本节课的知识和技巧，更要学习结构，了解本节课的知识在整个小学数学计算课程中的位置，因此笔者通过教材纵向的比较，挖掘知识之间的关联，沟通知识之间的联系，帮助实现知识结构化。

例如：在巩固提升时，笔者设置了一道习题(如图)：王老师在逛市场，发现了一个猜谜获奖的游戏，只要答对卡片下的数字，就能获得奖品，你想先翻哪张牌？通过要有顺序的翻牌，启发学生要先猜出第二张牌的大小，因为第二张牌在第一层上，第一层上的数与第二个乘数十位上的数无关，只需要算出24×2是多少，就可以得出第二张牌底下是4。其实就是在比较第一层得数和第二层得数的由来。通过这道习题的设置，让学生更充分理解两位数和两位数的笔算乘法，实际上是将其中一个乘数拆分成整十数和一位数，在计算的过程中，第一层实际上是在算个位数乘两位数。通过这样的习题设置，让学生对两位数乘两位数的算法和算理能同两位数乘一位数联系起来，知识之间的桥梁得以搭建。

在课接近尾声时，通过提问：“这是我们第一次用先分后合的方法来学习笔算乘法吗？”，勾起学生对以往知识的回忆，再展示三年级上册两位数乘一位数笔算的学习过程，让学生找一找先分后合的影子，先分的什么？合的又是什么，找到联系后再抛出问题“如果是三位数乘两位数呢，可以怎样解决？”通过比较两位数乘一位数、两位数乘两位数、三位数乘两位数的计算方法和计算过程，理清他们之间的区别与联系。至此，疏通了笔算乘法之间的脉络，学生能意识到两位数乘一位数、两位数乘两位数、三位数乘两位数之间计算的道理是相同的，这三个知识之间是密不可分的。

总之，在计算课中能做到前瞻后思、承上启下，致力于形成知识的整体架构，进行结构化教学，不仅有利于学生对记忆、技能和方法的迁移，学生在学习起来也有迹可循，建构好知识网络，还能为做好终身学习奠定重要基础。