基于极化定向角补偿的思茅松林地上生物量反演

张国飞, 岳彩荣, 罗洪斌, 谷 雷, 朱泊东

(西南林业大学林学院,云南 昆明 650224)

森林生物量能够反映森林生态系统的状态和变化规律，准确地获取森林生物量时空分布信息是生态学和全球变化研究热点之一[1-2]。星载合成孔径雷达(SAR)遥感在森林结构和生物物理参数反演中得到了广泛的应用，利用SAR数据估测森林生物量主要有后向散射系数的估测[3-7]、极化干涉模型的估测[8-10]和层析成像估测[11]等方法。其中后向散射系数估测存在饱和点问题，极化干涉技术和层析成像技术需要多基线或多频段的全极化SAR数据，对数据质量要求较高[11-12]。目前已有许多提取地物信息的极化分解方法[12-14]，这些方法也被应用于生物量估算[11-15]。Kumar等[15]采用Yamaguchi分解后的四分量与水云模型(water cloud model，WCM)对印度杜德瓦国家公园进行地上生物量估算；Santi等[16]采用L、C双频SAR数据和人工神经网络模型(artificial neural networks，ANN)反演森林蓄积量，模型决定系数为0.74，均方根误差为77 m3/hm2。

电磁波穿过电离层引起极化平面法拉第旋转(Faraday rotation)，使电磁波极化定向角(polarization orientation angle,POA)产生偏移[17-19]。极化定向角偏移影响微波散射特性和极化特征[20]。已有研究发现由于电磁波极化椭圆极化定向角的偏移，SAR极化分解后的散射特征在机理上存在模糊性[14,17-19]，如体散射高估和二面角散射低估。这种模糊性在森林参数反演时必然增加模型反演误差。已有学者对极化旋转和极化定向角补偿问题进行研究[14,19,21-22]，但有关探究极化定向角偏移补偿对森林地上生物量等森林参数反演的影响鲜见报道。

综上所述，本研究以ALOS PALSAR全极化SAR数据为数据源，通过Sinclair矩阵的酉变换来补偿极化定向角偏移，分析法拉第旋转补偿对SAR数据的影响；研究提出一种基于L波段散射特征的扩展极化水云模型；最后，采用Yamaguchi四分量分解参数和扩展极化水云模型估测思茅松林地上生物量。

1 材料与方法

1.1 研究区概况及样地数据

研究区位于云南省普洱市思茅区(100°49′～101°17′E，22°35′～22°53′N)。研究区年平均气温18 ℃，年均降雨量约1 500 mm，每年无霜期超过300 d，区内森林覆盖率67%，思茅松(Pinuskesiyavar.langbianensis)是主要优势树种[23]。

样地数据采集时间为2018年12月，设置了62个样地(样地面积为0.04 hm2)，其中36个样地用于考察法拉第旋转补偿对SAR数据的影响以及模型参数β值的确定，26个样地用于模型检验。对于乔木样地进行每木检尺，记录数据包括株数、胸径、树高、平均树高(表1)，通过所记录数据进行样地蓄积量计算。思茅松地上生物量(AGB，式中表示为AGB)计算公式为[23]：

(1)

式中：AGB表示林分每公顷地上生物量，t/hm2；N为样地思茅松株数；DBH为思茅松单株胸径,cm；H为思茅松单株树高,m；S为样地面积,hm2。

表1 思茅松样地林分参数

1.2 卫星数据

研究采用L波段PALSAR ALOS-2的高视角全极化SAR数据(high-sensitive full polarimetry)，卫星拍摄日期2016年5月11日，分辨率为6 m，中心入射角27.786°。

1.3 技术路线及极化定向角补偿

本研究的主要技术路线如图1所示。

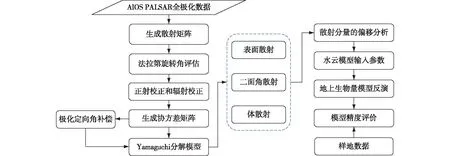
图1 技术路线流程图Fig.1 A technical road flowchart

ALOS PALSAR全极化数据极化定向角的偏移主要是由法拉第旋转和物体几何形状引起的[13,17,19,22,24-26]。研究对ALOS PALSAR单视复数(single look complex，SLC)数据进行法拉第旋转角估计和校正。

法拉第旋转偏移引起的散射矩阵M估计如下。

(2)

式中:M为具有法拉第旋转偏移的散射矩阵；S为不受法拉第旋转偏移影响的Sinclair散射矩阵中元素；HH表示发射水平极化波，接收回波中水平极化信号；HV表示发射水平极化波，接收回波中垂直极化信号；VH表示发射垂直极化波，接收回波中水平极化信号；VV表示发射垂直极化波，接收回波中垂直极化信号；Ω为法拉第旋转角。

由于圆极化电磁波不受法拉第旋转的效应影响[15,24]，故采用酉变换将散射矩阵M变换到圆极化基下[27]，变换公式为：

(3)

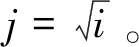
法拉第旋转角Ω可由圆极化散射矩阵获得[14-15]：

(4)

式中:*为复共轭；arg()为相位取值函数。

将法拉第旋转角Ω代入式(2)中，得到不受法拉第旋转偏移影响的散射矩阵S：

(5)

极化定向角补偿的目的是消除目标定向角随机分布引起的散射机制的模糊性，即由于物体几何形状和结构存在差异，两个定向角不同的物体产生相同的散射特征。在SAR数据极化分解前进行极化定向角补偿。通过相干矩阵的酉变换和旋转，极化定向角补偿后的相干矩阵表示为：

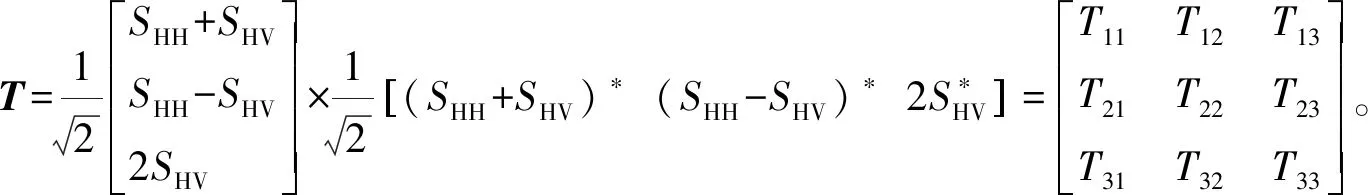
(6)

1.4 Yamaguchi分解

根据Yamaguchi算法[15,18]对ALOS PALSAR全极化图像进行目标分解，得到表面散射、二面角散射、体散射和螺旋体散射：

T=PsTsurface+PdTdouble+PvTvolume+PhThelix。

(7)

式中:Tsurface、Tdouble、Tvolume和Thelix分别表示表面散射、二面角散射、体散射和螺旋散射的相干矩阵元素，Ps、Pd、Pv和Ph分别为相应散射功率。

1.5 扩展极化水云模型

Attema等[28]提出的水云模型假定植被层是一个各向均质的散射分量和经森林双次衰减后地面的散射分量[29]。极化水云模型则为[30]：

(8)

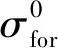
式(6)中没有考虑林冠空隙，在真实森林场景中，尤其是低密度林分中，电磁波通过林冠空隙返回信号[31]。考虑林冠空隙后，则有：

(9)

式中:η为面积填充因子，是关于森林透射率的函数。

考虑林冠空隙因素，森林植被衰减层透过率Tfor可表示为：Tfor=1-η+ηe-δh，可用地上生物量B描述[15,32]，即Tfor=e-βB，B表示地上生物量，β表示经验参数。结合Tfor，则有：

(10)

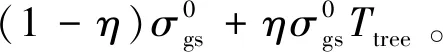
(11)

(12)

研究的算法检验统计量包括决定系数(R2)和均方根误差[RMSE，式中记为σ(RMSE)]。

(13)

(14)

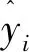
2 结果与分析

2.1 法拉第旋转角的估计

利用式(4)评估ALOS PALSAR全极化数据法拉第旋转偏移情况，并根据式(2)、(3)、(4)进行了补偿。未进行补偿的法拉第旋转角度为-0.393°～0.393°，平均值为0.006 43°，标准偏差为0.022 5°(图2)。

图2 补偿前后的法拉第旋转角及其直方图Fig.2 Faraday rotation angle image before and after compensation

补偿后的法拉第旋转角近似正态分布，图像相对平滑、均匀。平均值为0.002 36°，与补偿前相比减少了0.004 09°，标准偏差为0.001 6°，与Kumar等[15]的研究结论一致。

2.2 实测地上生物量与体散射的回归分析

分别对补偿前和补偿后ALOS PALSAR全极化数据进行Yamaguchi分解获得体散射分量，考察极化定向角补偿对36个样地体散射值的影响。图3显示了36个样地补偿前和补偿后的体散射值比较，极化定向角补偿后所有样地的体散射均减小,类似情况在相关文献[15,21-22]中已有报道。

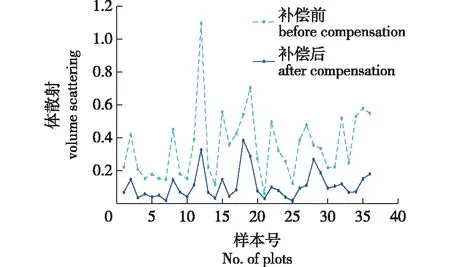
图3 体散射值的比较Fig.3 A comparison of volume scattering values

实测地上生物量(AGB)与体散射的回归分析表明极化定向角补偿后的体散射与实测地上生物量的回归模型(R2=0.332)要好于未进行极化定向角补偿的体散射与实测地上生物量的回归模型(R2=0.214)，见图4。

图4 实测地上生物量与体散射分量的非线性回归Fig.4 The regression between aboveground biomass (AGB) and volume scattering obtained

图5 估测地上生物量和实测地上生物量的散点图Fig.5 The relationship between the field-estimated AGB and the modeled AGB

2.3 基于扩展极化水云模型的森林地上生物量反演

利用扩展极化水云模型公式(12)求解生物量，其中模型参数β值由公式(15)计算而得。将前面36个样地对应的Yamaguchi分解后总后向散射系数、体散射分量、表面散射分量和二面角散射分量分别输入到式(15)中得到每个样地β值，以36个样地β的算术平均值作为β的估测值[15，33-34]。

(15)

36个样地应用公式(12)估测地上生物量和实测地上生物量的散射图见图5。在未对图像极化定向角补偿的情况下，实测地上生物量与预测地上生物量的决定系数为0.316，均方根误差(RMSE)为68.23 t/hm2；极化定向角补偿后，决定系数提高到0.705，均方根误差为28.59 t/hm2。说明极化定向角补偿后，有利于地上生物量的反演精度提升。

为了检验公式(12)的推广精度，另外选择了未参与估测β值的26个样地进行生物量估测试验，估测结果与实测之间具有较好的一致性，其决定系数R2为0.644，均方根误差为23.11 t/hm2，散点图见图6。

依据式(12)计算的研究区地上生物量分布图见图7。与Google光学遥感图像对比发现，在道路、建筑、裸地、水体等非森林区域的地上生物量值几乎为0(蓝色)；在草地、耕地区域，地上生物量较小(浅绿色)；森林区域，地上生物量较大(绿色),尤其在茂密森林区域，生物量最大(黄红色)，最大值达到382 t/hm2。

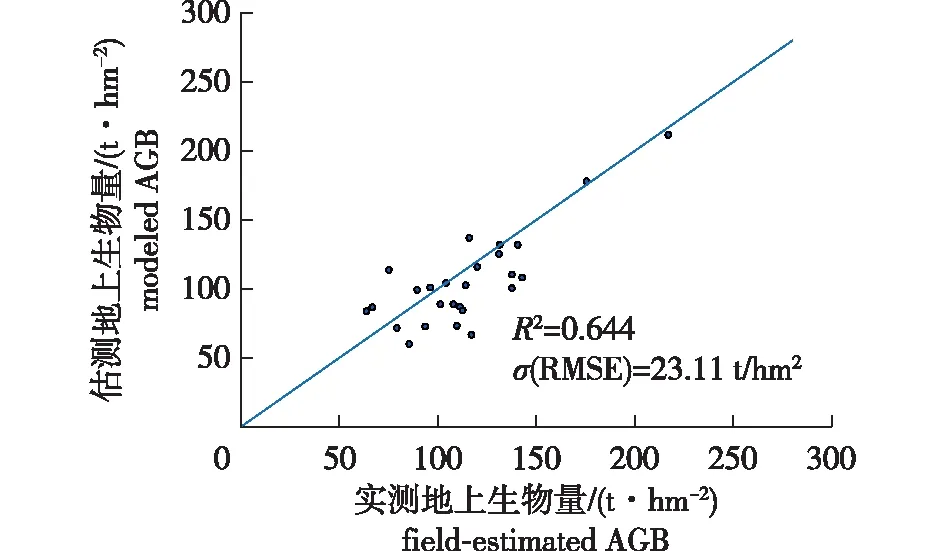
图6 26个验证样地估测地上生物量和实测地上生物量的散点图Fig.6 Relationship between the field-estimated AGB and the modeled AGB of 26 samples

图7 研究区地上生物量分布图Fig.7 Distribution map of aboveground biomass in the study area

3 讨 论

1)极化定向角的偏移主要是由于法拉第旋转和物体结构特性引起的[13,19,22]。研究通过Sinclair矩阵的酉变换来补偿极化定向角偏移，补偿后的(Yamaguchi四分量中)体散射分量数值在36个样地中均有减小,即极化定向角的偏移使体散射分量被高估，与相关研究结论一致[15,21-22]。补偿后的体散射分量与森林地上生物量的回归模型较未补偿前效果更好(R2从0.214提高到0.332)。

2)扩展极化水云模型是一种考虑二面角散射的极化水云模型。研究中采用Yamaguchi四分量参数和扩展极化水云模型估测思茅松林地上生物量；ALOS PALSAR全极化数据进行极化定向角补偿后，地上生物量反演精度得到提升[R2从0.316提高到0.705，均方根误差(RMSE)从68.23 t/hm2减少到28.59 t/hm2]。在26个检验样地也有较好的反演精度(R2=0.644和RMSE为23.11 t/hm2)。

3)研究以普洱市思茅地区的思茅松林为研究对象，模型参数仅需通过少量样地实测数据计算确定，此次反演具有较好的精度，且估测地上生物量分布和Google光学遥感影像地物分布具有较好的一致性，但模型在其他区域和树种是否具有普适性尚待进一步验证，今后应将SAR数据与光学遥感影像融合反演地上生物量。另外，研究中PALSAR ALOS-2的全极化SAR数据和生物量地面调查数据间隔31个月，本研究对生物量样地数据参照相关文献[23,35-37]报道的生物量年生长率进行了时间差修正，这可能也是影响反演精度的因素之一。

4)Michelakis等[38]利用基于L波段SAR数据和水云模型对伯利兹松树草原地区的稀疏乔木进行了地上生物量估算，模型R2和RMSE分别为0.70和25 t/hm2，模型精度稍高于本研究，但本研究区域属于山区，地形有较大起伏。Santi等[16]采用L、C双频SAR数据和人工神经网络模型(artificial neural networks，ANN)反演森林蓄积量，模型相关系数为0.86，RMSE为77 m3/hm2。Peregon等[39]利用L波段SAR数据和水云模型对西西伯利亚森林区域进行地上生物量反演，模型R2为0.35～0.49，RMSE为46～55 t/hm2，模型精度比本研究的稍差。Kumar等[15]采用L波段SAR数据和扩展极化水云模型在印度杜德瓦国家公园进行地上生物量估算，模型R2和RMSE分别为0.78和59.77 t/hm2，模型决定系数高于本研究，但模型精度低于本研究。

综上所述，本研究中以L波段全极化SAR数据为数据源，采用极化定向角补偿后的Yamaguchi分解分量和扩展极化水云模型能够较高精度地估测森林地上生物量。

4 结 论

基于PALSAR ALOS-2数据，以云南思茅松林为研究对象，研究了法拉第旋转效应导致的极化定向角补偿方法，分析了极化角补偿对思茅松林微波体散射求解的影响，在此基础上，采用极化水云模型对思茅松林地上生物量进行反演试验。研究结果表明，从Yamaguchi分解结果来看，由于极化定向角的偏移，导致森林的体散射分量被高估，极化定向角补偿后，体散射后向散射系数得到有效修正；极化定向角补偿后体散射系数与森林地上生物量对数回归的决定系数较未补偿前得到了提高(R2从0.214提高到0.332)；极化定向角补偿后，扩展极化水云模型的森林地上生物量反演精度也较补偿前的有了明显提高，模型决定系数R2从0.316提高到0.705，均方根误差从68.23 t/hm2降低到28.59 t/hm2，经独立样本检验，估测结果地上生物量和实测地上生物量之间R2为 0.644，均方根误差为23.11 t/hm2。

致谢部分样地调查数据由中国林业科学研究院提供。