床垫用垂向变刚度空气弹簧静力学特性及其计算模型
2021-11-30晁垚申黎明刘明鹏张宏玉
晁垚,申黎明,2*,刘明鹏,张宏玉
(1. 南京林业大学家居与工业设计学院,南京 210037;2. 南京林业大学林业资源高效加工利用协同创新中心,南京 210037)
人的一生大约有三分之一的时间是在睡眠系统(床架和床垫)上度过的,因此人与床垫交互过程产生的界面特性对于人的卧姿舒适度、睡眠质量以及睡眠健康均有不可忽视的影响。界面特性包括热舒适度与支撑特性,与床垫结构有关。传统床垫一般是由铺垫层和支撑层(弹簧层)组成的层状复合结构。铺垫层主要影响床垫的缓冲特性与界面温度分布,弹簧层主要影响床垫的刚度特性,即支撑特性;床垫刚度的物理意义为床垫在受压后抵御弹性变形的特征。因此,铺垫层结构和材料主要影响界面温度分布、被褥微环境热舒适度[1-2]以及“人-床垫”界面的压力分布[3-4];弹簧层主要影响与生物力学相关的支撑特性,体现在卧姿脊柱形态以及关节屈曲角度和生物力学[5-6]。因此,弹簧层的支撑作用对于保障人体骨骼肌肉处于最佳受力状态具有重要作用。此外,不同用户由于人体测量学特征的差异,如身体轮廓、体型、重量分布等,在使用床垫时会产生不同的界面压陷形状和不同的人体生物力学作用,因此对床垫的支撑具有不同的需求[7-8]。研究表明,长期卧床的群体需要避免产生压疮[9],而对于成长中的青少年而言,床垫良好的支撑特性对于骨骼肌肉的正常生长极为重要。因此,理想床垫弹簧层应该能够根据用户使用床垫时的支撑情况而实时调节刚度以满足个性化以及不同卧姿的支撑需求,尤其是使用户获得自然的卧姿脊柱形态[10-11]。在过去的10多年中,变刚度床垫的研究对象主要是防压疮护理床垫[12],其支撑结构是刚度可通过改变充气量调节的条状、块状气囊,一般不加铺垫层。由于气囊床垫主要用来防止压疮,因此其功能是缓解界面压力[13],调控过程并未考虑人体骨骼肌肉的生物力学作用。除气囊外,用于工效学垫类产品的非线性刚度混合螺旋弹簧[14]在使用中可以产生变化的刚度,然而刚度变化范围在弹簧生产出来便固定,无法在实际工作中实现个性化实时调节。综上,目前床垫刚度调节研究的局限性在于:1)主要关注医用护理床垫,对家用变刚度床垫研究较少;2)床垫使用的气囊体积较大、变形无法预测,无法精确调控其刚度与形变以实现人体局部支撑变化的需求;3)非线性钢弹簧使用过程中刚度无法个性化调节。为了研究家用变刚度床垫以满足个性化的卧姿支撑需求,首先需要解决床垫弹簧层刚度个性化调节的问题。因此,笔者提出:1)是否可以设计一种承受轴向载荷、产生轴向变形的空气弹簧,并提供类似于螺旋钢弹簧的点状支撑;2)是否可以实现空气弹簧的刚度非线性调节;3)是否可以建立计算模型,描述空气弹簧载荷与高度之间的关系,作为床垫支撑特性调节的工程控制方法。
为了解决以上问题,本研究提出一种用于床垫的垂向变刚度空气弹簧设计方法,并通过准静态单轴压缩实验分析空气弹簧刚度特征及影响因素,为空气弹簧的设计提供依据;同时,提出一种建立空气弹簧的压缩量、载荷与气压之间关系计算模型的方法,用于实际工程控制中床垫支撑特性的调控。
1 材料与方法
1.1 空气弹簧制备
本实验所用空气弹簧样品委托浙江某气囊生产厂家制样。本实验选用热塑性聚氨酯(thermoplastic polyurethane,TPU)涂层织物复合材料制作空气弹簧。TPU涂层厚度为0.5 mm,限于企业现有材料约束,只有两种密度,即210 D及840 D(D,Denier,其含义是单根纤维每9 000 m质量为210和840 g);二者区别在于纤维线径,840 D线径稍大,相应力学强度也较大。以密度为840 D的原料为例,其外观与细节如图1a所示。本研究设计了一种主要承受轴向载荷的空气弹簧,其结构如图1b所示,由1层或多层曲囊气室堆叠构成,h为充气后的总成高度,h0为单层曲囊展开后高度;曲囊未充气展开时各面均为圆形平面,其直径由于两片材质边缘处的粘合而损失10 mm,成品半径为R0,如图1c所示。空气弹簧充气展开后由近似球冠面围合成曲囊气室,各层曲囊之间连通,最下层曲囊中心装配接头,用来与气源连接。实验用空气弹簧样品共有1层、2层、3层3种结构,如图1d所示。充气展开后几何参数如表1所示,其中容积通过排水法测得。
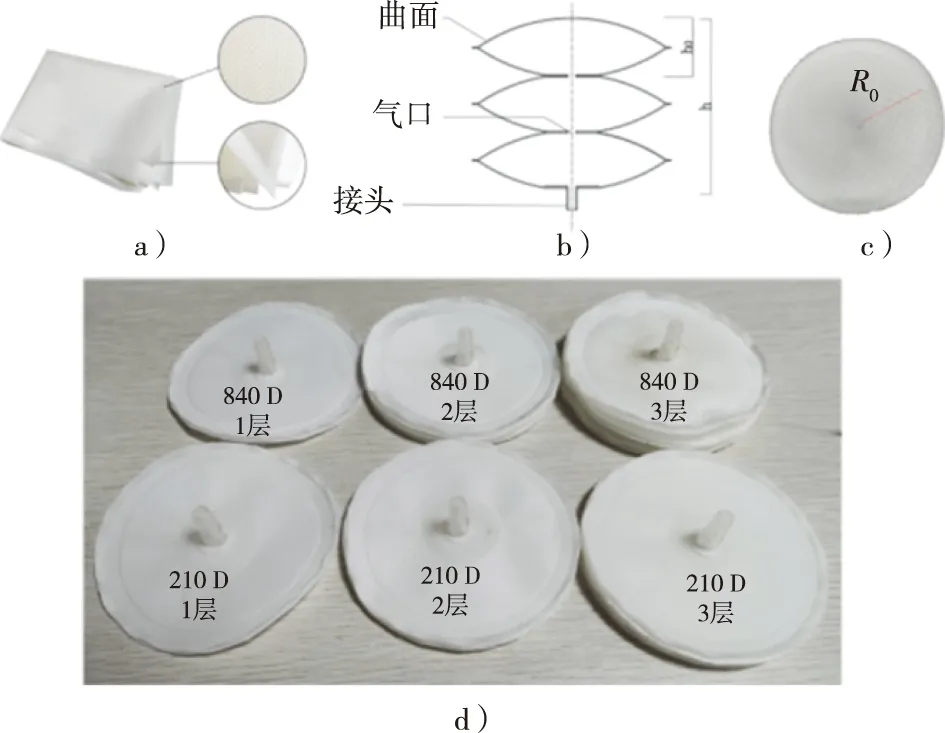
图1 材料及空气弹簧结构、试件Fig. 1 Material, structure and specimens of air spring
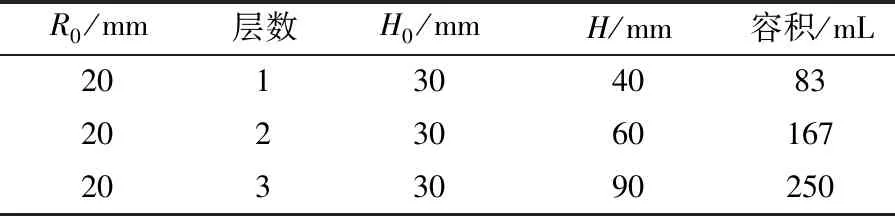
表1 空气弹簧试件尺寸参数Table 1 Parameters of air spring specimens
1.2 实验设备与仪器
本实验为准静态单轴压缩实验,所用设备为力学实验机(Shimadzu,Japan)以及气压测量仪。气压测量仪由气压传感器及Arduino开发板制作,并经过机械式气压表及标准大气压校准。力学实验机压头为不锈钢圆盘,直径100 mm,加载与卸载速率为25 mm/min。气源为加可控硅模块改装的可调压气泵。实验设定信息如表2所示,实验连接及加载过程如图2所示。

表2 仪器设备工作信息Table 2 Working information of equipment and instruments
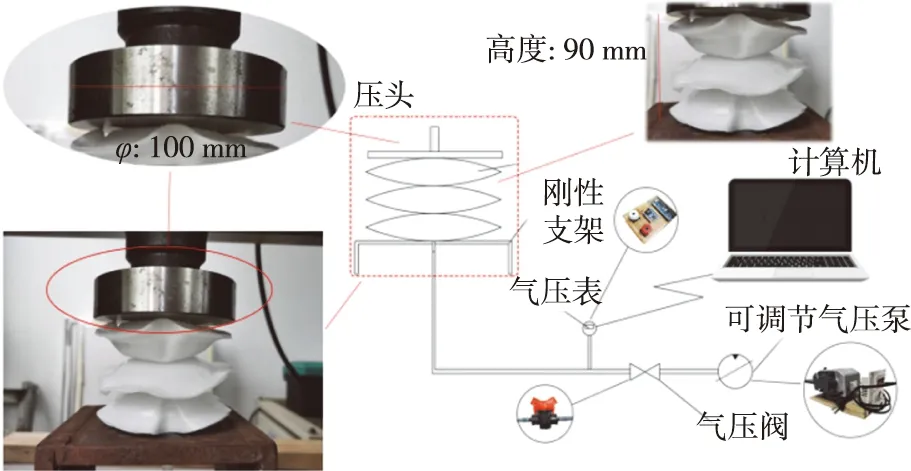
图2 实验设备连接图及压缩过程Fig. 2 Diagram of experiment connection and compression process
1.3 实验设计
实验各因素及详细信息如表3所示。

表3 实验因素信息Table 3 Information of experimental parameters
实验流程如下:
1)调节实验机压头与空气弹簧上表面接触至预载荷1×10-3kN,调节空气弹簧内部气压为10 kPa,压力稳定后关闭气阀,将力学实验机调零。
2)1层、2层、3层空气弹簧轴向压缩距离分别为20,30,60 mm。启动力学机及气压测试仪,记录“位移-载荷”“位移-气压”数据。
3)加载试束后,以同样的速率卸载至载荷为0 kN,并同步记录空气弹簧内部气压。
4)调节初始气压至其他水平,重复上述过程,直到所有的实验条件全部测试完毕。每种工况每个样品进行1次实验。
1.4 数据处理
本实验所有数据使用MATLAB 2016 Ra处理,分析内容如下:
1)结合理想气体压缩过程的基本理论与实验现象,分析空气弹簧在不同实验条件下的载荷与气压变化特征以及各实验因素对刚度、内部气压的影响;
2)建立空气弹簧“位移-载荷”“位移-气压”计算模型,用于实际工程控制中刚度调控。
2 结果与分析
2.1 刚度与初始压强、容积的关系
空气弹簧刚度的物理含义是其抵御弹性变形的能力,表示空气弹簧被压缩的难易程度;数学含义为载荷对压缩距离的微分。刚度越大,压缩单位长度需要的外力越大,空气弹簧越不易被压缩。
为了分析空气弹簧刚度与内部气压和容积的关系,需要通过刚度的数学含义并借助气体压缩过程物理状态方程分析。本实验压缩速率较低,压缩过程可视为恒温过程,假设空气弹簧内部为理想气体,则满足公式(1):
pv=cRT
(1)
式中:p为压缩过程中空气弹簧内部压强;v为气体体积;c为气体质量;R为通用气体常量,通常取(8.314±0.000 26) J/(mol·K);T为气体热力学温度。
空气弹簧的刚度表达式为:
k=dFload/dl
(2)
式中:k为空气弹簧的刚度;Fload为压缩过程中载荷,是关于压缩量的函数,表示为Fload=f(l);l为压缩量。根据静力学平衡原理,载荷可以表示为:
Fload=ps
(3)
式中:p为压缩过程中空气弹簧内部压强,表示为p=g(l),随着压缩量增加而增大;s为压缩过程中空气弹簧的实际承压面积。由于本实验所用空气弹簧表面为球冠面,压头与空气弹簧的接触面积随着空气弹簧压缩量的增加而增大。因此,实际承压面积s也是关于压缩量的函数,表示为s=u(l)。刚度与压强和面积之间的函数关系式为:
(4)
联立式(1)、(2)、(3),刚度与容积和面积的函数关系式为:
(5)
式中,v为空气弹簧内封闭气体的体积。
以材质密度210 D的空气弹簧为例,3种空气弹簧在9种初始气压工况下的“位移-载荷”结果如图3所示。
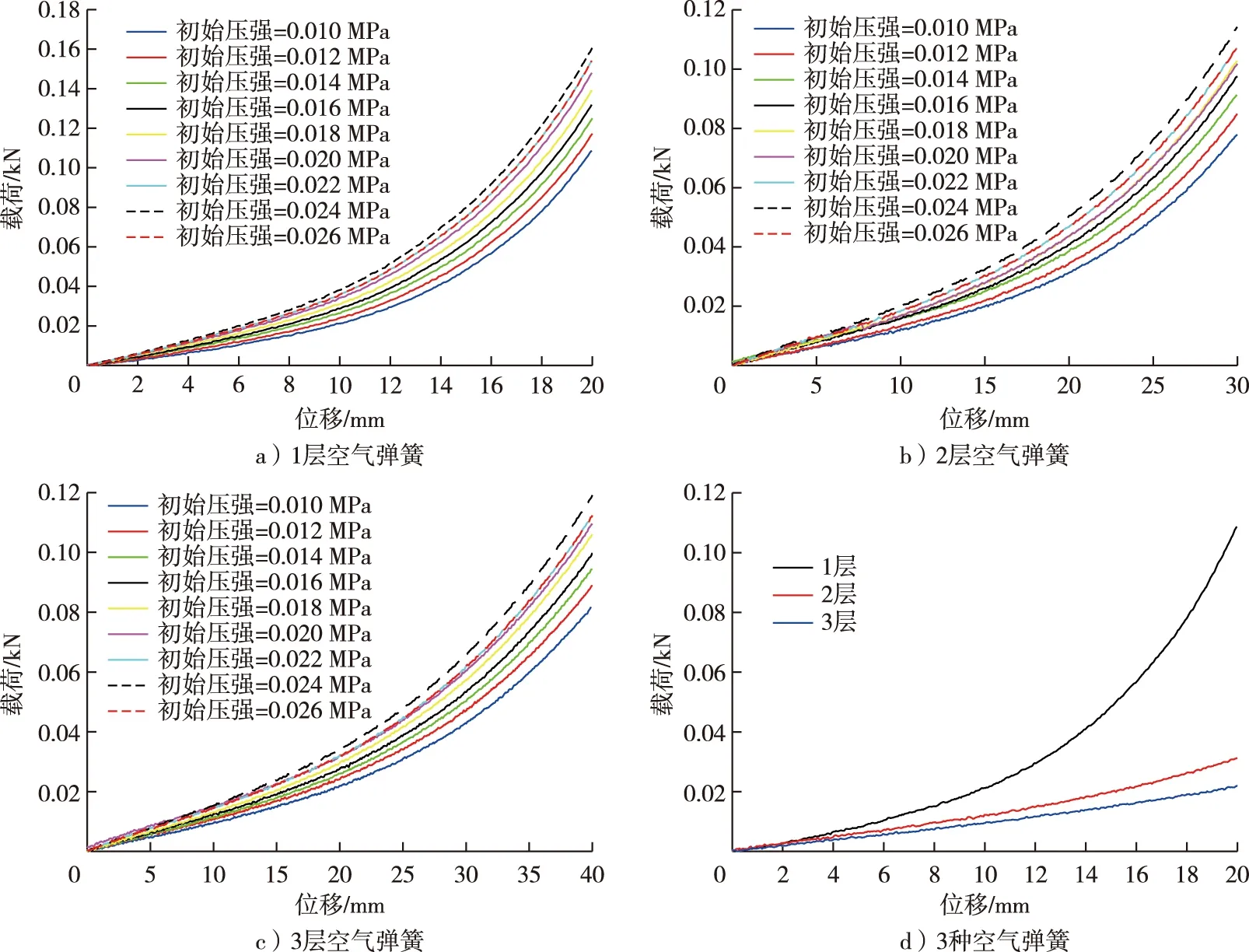
图3 “位移-载荷”压缩曲线Fig. 3 Compression curves of displacement-load
结合式(4)、(5)与图3可得:
1)从式(3)可以看出,空气弹簧的刚度由气压变化率以及接触面积变化率共同决定。空气弹簧刚度与气压p之间存在正相关关系。空气弹簧内气体压强越大,刚度越大,压缩同样位移需要的载荷越大,这与图3a~c的趋势一致。
2)从式(5)可以看出,空气弹簧的刚度由体积变化率以及接触面积变化率共同决定,与接触面积成正比,与体积成反比。当初始压强相同时,空气弹簧初始容积越大,压缩同样位移时压强变化率越小,空气弹簧的刚度越小,压缩所需要的载荷也就越小,与图3d的规律一致:同样初始压强工况下,压缩相同位移时,3层空气弹簧气压变化率最小,刚度最小。空气弹簧刚度与容积之间存在非线性负相关关系。
3)空气弹簧的刚度可类比于普通螺旋弹簧的劲度系数k,不同之处在于普通螺旋弹簧的劲度系数为定值,受力与变形之间的关系满足胡克定律。空气弹簧刚度为容积和气压变化率的函数,为变化值。
2.2 内部气压与压缩量的关系
所有空气弹簧试件在9种工况的“位移-气压”曲线趋势一致,以材料密度210 D、1层空气弹簧为例,如图4所示,空气弹簧压缩位移与内部气压之间均呈现非线性正相关关系,随着压缩位移增加,空气弹簧内部气压非线性增加。
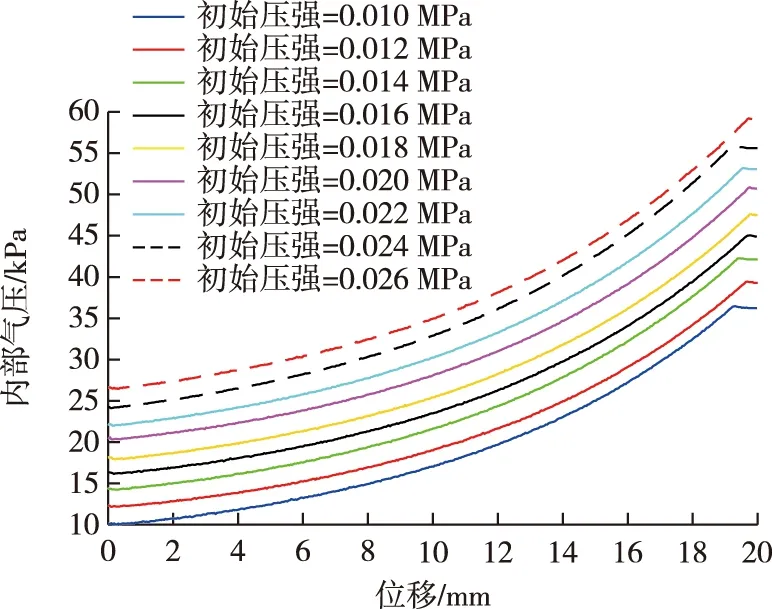
图4 “位移-气压”曲线Fig. 4 Curves of displacement-inner pressure
2.3 刚度与材料密度的关系
以1层空气弹簧、初始气压10 kPa的压缩曲线为例,两种密度材料的空气弹簧“位移-载荷”曲线如图5所示。其余工况下二者关系呈现一致性规律,密度840 D材质的空气弹簧曲线在上方。
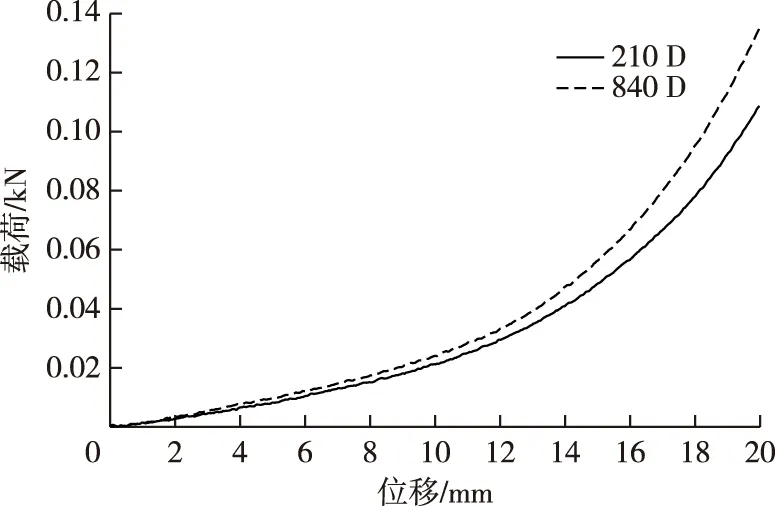
图5 不同材质密度空气弹簧的“位移-载荷”曲线Fig. 5 Curves of displacement-force respect to different material densities
分析图5可知,空气弹簧材质密度与其刚度之间存在正相关关系,当初始容积、初始气压以及压缩行程相同时,材质密度越大,压缩所需的载荷越大。这可能是受到材料织物层纤维线径的影响。由于空气弹簧受压后织物层纤维在气体作用力下产生张力而被拉伸,而线径较大的纤维发生同样拉伸距离需要的载荷较大,因此表现为空气弹簧的刚度较大。
2.4 滞后性
以密度210 D、3层空气弹簧为例,在初始内压26 kPa工况以同样的速率加载、卸载,“空气弹簧高度-载荷”曲线如图6所示。分析图6可得:
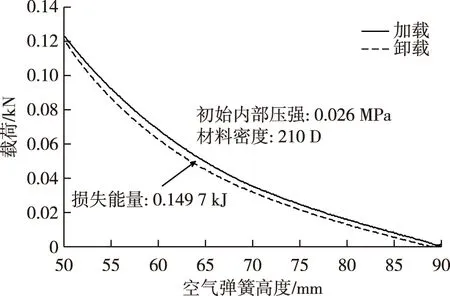
图6 加载-卸载曲线Fig. 6 Curves of loading and unloading
1)空气弹簧加载与卸载曲线之间存在偏离,可能是由于压缩过程中空气弹簧内的封闭气体与外界空气之间发生了热量交换而损失了部分内能。由于实验压缩速率较低,因此空气弹簧内气体在压缩过程中视为恒温、非绝热过程,封闭气体温度增益非常缓慢,从而由进入大气的热流来补偿。加载曲线与卸载曲线围合面积即为加载与卸载过程中损失的能量。
2)加载与卸载过程损失的能量很小,二者曲线基本重合,近似认为加载与卸载过程可以用同样的函数表示,二者互为逆过程,即载荷以及内部气压可表示为弹簧高度或位移的函数。
3 垂向变刚度空气弹簧力学计算模型
空气弹簧力学计算模型的建模方法一般有两种,一种为基于实验数据的函数系数拟合法,一种为基于理想气体状态方程和气体动力学方程的参数化建模法[15]。拟合参数得到的模型变量只有压缩量,由于变量少、计算过程简单,因此非常适用于工程控制;而参数化建模变量则是空气弹簧几何尺寸、气体状态相关参数。对于不规则形状和复杂几何形状的空气弹簧,参数化建模需要对空气弹簧几何形状做近似处理,因此预测精度受到影响,且计算过程较为复杂,适用于空气弹簧设计过程的刚度预测分析。本实验设计的空气弹簧充气展开后为近似于球冠面的曲面围合而成,实际工作过程中高度、容积、接触面积等所有的尺寸均在变化,参数化建模比较复杂,并不适用于工程控制。为了准确描述空气弹簧的力学性能,并用于实际工程控制中调节“人-床垫”界面压陷形状,本研究选择拟合参数的方式同时考虑多种变量,建立计算模型。
3.1 “位移-载荷”计算模型
经过上述分析可知,空气弹簧的载荷与压缩量以及初始内压之间均存在函数关系。因此通过多项式拟合的方式建立任意初始压强的“位移-载荷”函数表达式[16]。将载荷F表示为位移l的多项式函数,对F微分得到F关于压缩量的导函数,即刚度k的函数。
以空气弹簧在初始气压为10 kPa工况的实验数据为例,通过多项式拟合法建立同时考虑初始气压与压缩量的计算模型。压缩位移与载荷曲线的拟合结果如表4所示,随着拟合幂次增加,均方差逐渐减小,可信度逐渐增加;但当n>3时,各指标变化并不显著。因此,在工程控制中,最高幂次n=3时即可满足工程控制需求。

表4 多项式拟合结果Table 4 Polynomial fitting results
“位移-载荷”的多项式函数表达式为:
Fp=ap1ln+ap2ln-1+…+apnl+ap(n+1)
(6)
式中:Fp为空气弹簧载荷;l为空气弹簧压缩位移;n为多项式最高幂次;apj为幂次降序的多项式系数,j=1,2,…,n+1。
定义空气弹簧的压缩量幂矢量l=(ln,ln-1,…,l,1)T,多项式系数可以表示为矢量ap=(ap1,ap2,…,apn,ap(n+1)),代入式(6),可以得到矩阵表示的多项式拟合关系:
Fp=apl
(7)
本实验工况为9种初始气压,从10到26 kPa,间隔为2 kPa,每种空气弹簧拟合得到9组3次多项式函数,但是此9组多项式函数只能分别描述对应9种初始内压工况的“位移-载荷”,对于实验未包括的初始内压工况,该组函数则无法应用。观察9组“位移-载荷”曲线的差异,可推断9组曲线3次多项式函数各幂次项系数与初始气压之间有关系,因此将初始气压的影响考虑在内,进行第二次拟合,此次拟合幂次项系数与初始气压之间的函数。将9组3次多项式函数的各幂次项系数按照初始气压从低到高单调排列,得到不同初始气压的幂次项系数矩阵a,则空气弹簧“位移-载荷”用矩阵表示为:
F=al
(8)
式中:F为载荷,F=(F1,F2,…,Fk),下标k表示不同初始内压下的载荷,在本实验中,k=9;l为压缩位移幂矢量;a为拟合多项式幂次项系数。
(9)
初始气压用矢量P表示,P=(P1,P2,…,Pk),其中k=9,Pi表示第i条压缩曲线对应的初始内压。矩阵a的行向量表示同一初始内压下空气弹簧拟合多项式函数从最高幂次项到零幂次项的系数;矩阵a的列向量表示多项式各幂次项系数随着初始内压变化的规律,按照初始气压从低到高排列。因此,将各列系数与9种初始内压采用多项式拟合参数。
二次拟合时将初始内压p视作自变量,a中各列元素视作因变量,多项式函数表达式为:
aj=bj1pm+bj2pm-1+…+bjmp+bj(m+1)
(10)
式中:m为二次拟合多项式最高幂次;j为系数在矩阵a中的列号;bjl为幂次降序的多项式系数;l=1,2,…,m+1;b为系数矩阵。
(11)
定义不同初始内压为压力幂矢量P=(pm,pm-1,…,p,1)T,在本实验中p的取值为10~26 kPa,间隔2 kPa,9种工况压缩曲线拟合得到的多项式系数矢量a可以表示为:
a=bp
(12)
将式(12)代入式(7),得到任意初始气压工况的空气弹簧压缩曲线拟合多项式函数:
Fp=(bp)Tl
(13)
对式(13)微分,就得到空气弹簧变刚度表达式:
(14)
式中:kp为初始内压为p时空气弹簧刚度函数;Fp为初始内压为p时空气弹簧载荷。
下面使用一个算例检验二次拟合的函数准确性。
选择初始内压为26 kPa,使用式(13)模拟计算1层空气弹簧压缩0~20 mm过程中的载荷,拟合时n=3、m=6,拟合函数和计算结果与实验测量结果比较;再随机设定一种非实验过程的初始气压,如p=19 kPa,使用式(13)计算空气弹簧在压缩过程中的载荷,并与p=26 kPa的实验数据相比,结果如图7a、b所示。该初始气压工况下载荷计算模型如下(R>0.99):
F=0.000 022 39·l3-0.000 027·l2+0.004 16·l-0.001 39
从图7a中可以看出,二次拟合的多项式函数能够精确地表示空气弹簧压缩过程。初始内压19 kPa时空气弹簧的预测载荷如图7b下方的曲线所示,小于初始内压26 kPa的载荷,这与图3表现出的规律相符合,表明该方法拟合得到的工程控制计算模型较为精确,达到了工程应用的要求。
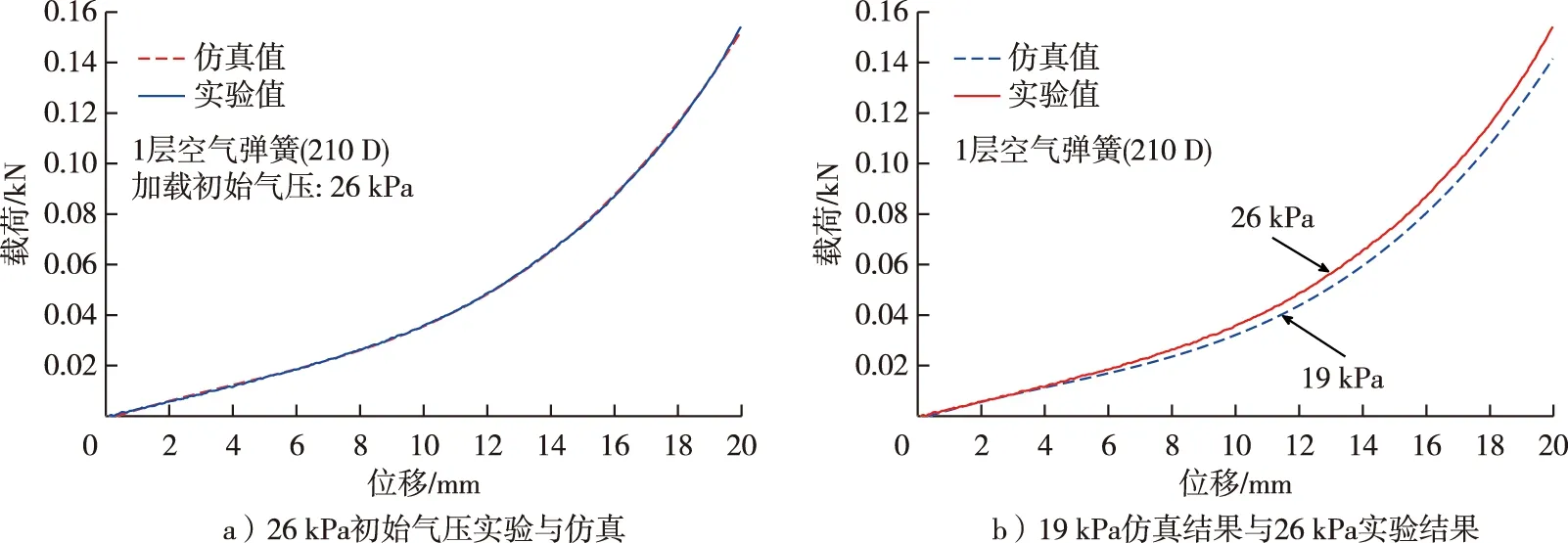
图7 位移-载荷的模拟结果与实验比较Fig. 7 Comparison of displacement-load simulation results with experimental results
至此,给定任意初始内压p,即可根据式(13)精确计算空气弹簧任意平衡位置的载荷,也可以根据任意平衡位置的载荷计算空气弹簧的压缩位移或高度。
3.2 “位移-气压”计算模型
与“位移-载荷”计算模型拟合思路相同,通过二次拟合的方法建立任意初始气压工况的空气弹簧内部压强与位移之间的计算模型,最终确定为3次多项式,m=6,n=3。
下面使用一个算例验证计算模型的准确度。
以材质密度为210 D的1层空气弹簧在初始气压26 kPa工况压缩过程为例,将拟合多项式函数模拟计算气压值与实验测量气压值比较,结果如图8a所示,二者曲线几乎重合,表明模拟计算结果可靠。
给定试验范围之外的任意初始压强,如19 kPa,拟合多项式计算值与初始压强26 kPa条件下实验值结果如图8b所示,此时预测模型如下(R>0.99):
p=0.002 5·l3+0.000 6·l2+0.515 6·l+18.948 9
压缩量为0 mm时,即l=0 mm,气压计算模型的预测值为常数项18.948 9 kPa,与初始压强19 kPa差异很小。从图8b可以看出,19 kPa工况的“气压-位移”曲线在26 kPa工况曲线的下方,与图4的趋势一致。
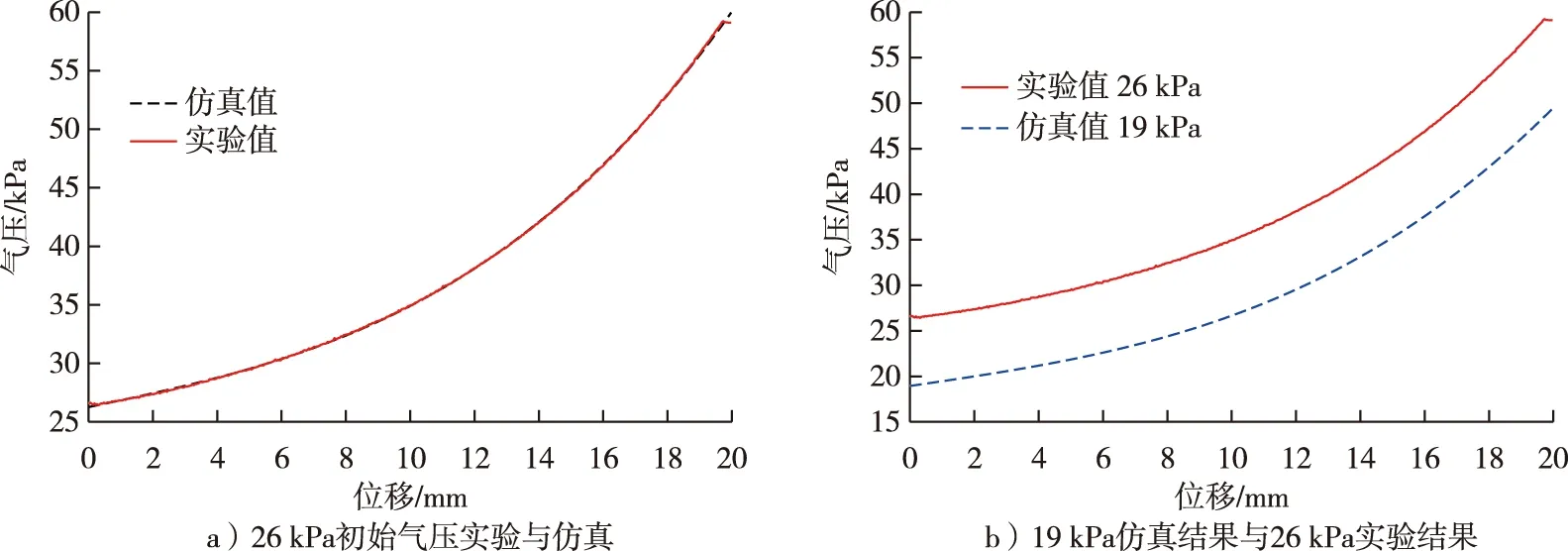
图8 位移-气压的模拟结果与实验结果比较Fig. 8 Comparison of displacement-pressure simulation results with experimental results
至此,给定任意初始压强,即可根据任意平衡位置时空气弹簧内部气压计算压缩量,从而可以通过空气弹簧高度描述“人-床垫”界面压陷形状,获得卧姿脊柱形态。以上方法和结果为变刚度床垫设计和调控提供了基本依据和可行性验证。本研究所提出的垂向变刚度空气弹簧相对于传统螺旋钢弹簧以及传统气囊而言具有以下优点:
1)普通螺旋钢弹簧以及非线性钢弹簧的刚度出厂即确定,而空气弹簧在尺寸确定时可以通过调节初始气压获得不同刚度,灵活多变;在工作过程中通过调节内部气压而改变工作过程中刚度以满足人体卧姿变化时床垫的支撑需求;
2)空气弹簧受压时主要发生垂向形变,运动轨迹与形变明确,容易获得精确的高度与载荷、内部压强之间的关系,为个性化卧姿脊柱形态调节提供了可能条件,且工程调控方便。
4 结 论
通过对不同结构和材质密度的空气弹簧进行准静态单轴压缩实验与结果分析,可以得出以下结论:
1)空气弹簧在轴向压缩过程中,刚度与气压呈现非线性变化。压缩量越大,刚度越大;内部气压呈现非线性增加的趋势。通过改变工作过程中平衡位置的气压,可以实现工作过程中刚度的个性化调节。
2)空气弹簧的刚度与初始容积之间为非线性负相关关系,与初始内部压强之间为正相关关系,与材质密度大小之间为正相关关系。在设计与工程控制中可以通过改变以上相关参数实现刚度调节。
3)使用多项式拟合参数的方法可以获得空气弹簧任意初始气压工况下载荷、内部气压与压缩量之间的计算模型,从而可以根据实时气压与载荷计算及调控空气弹簧的工作高度,为变刚度床垫设计及工程控制方法提供了可能条件与基础理论依据。
