风电场一次调频能力的深度挖掘研究及应用
2021-11-30霍红岩
周 磊,张 谦,霍红岩,齐 军
(1. 内蒙古电力科学研究院,呼和浩特 010020;2. 内蒙古电力调控中心,呼和浩特 010020)
0 引言
随着新能源优先开发、优先调度等政策的实施,在享用清洁绿色能源的同时,也给电力系统的安全稳定运行带来了一系列挑战。“三北”地区的火电机组已逐步进入深度调峰状态,在冬季供热机组仍需要保证供热的情况下,电力系统可用的一次调频响应资源逐步减少,造成电力系统频率安全风险不断加大[1-6];与此同时,随着特高压直流输电工程的大量投产及异步电网的联网运行,电力系统的功率平衡及调频难度不断加大,直流大功率闭锁(相继闭锁)对电力系统频率安全造成了严重威胁[7-10]。因此,针对风电主动参与电力系统调频,以提升电力系统频率安全水平的研究与应用正在积极开展。
目前,风电参与电力系统调频的研究主要集中在单机控制策略方面,国内外学者提出了多种控制方法,可根据电力系统频率的变化快速调节变速风电机组输出的有功功率,实现风电在电力系统发生扰动期间对电力系统频率的支撑。主要的控制方法包括桨距角控制[11]、惯量控制[12-13]及转速控制[14]等。同时,还有很多学者研究了通过模拟同步发电机摇摆方程,使变流器具备类似同步机的阻尼特性,即虚拟同步机技术,以此来参与电力系统调频。
上述研究奠定了风电机组参与电力系统一次调频的理论基础。但在实际应用过程中,上述文献提出的控制方法需要对风电机组的主控系统、变流器及桨距控制系统的控制策略进行较大幅度的改动,甚至需要加装设备,这对于已运行的风电场而言,存在较大的不可控性及较高的成本投入。为了使风电机组具备频率下扰工况下的一次调频响应能力,上述文献提出通过变桨、转速控制使风电机组长期运行在非最佳工况点,以此使风电机组能在频率下扰工况下预留容量来参与频率响应,但这会造成风电场效益下降;或采用惯量控制策略,在频率下扰工况下通过降低风电机组的转速来提供风电机组有功功率的上升裕量,但在转速恢复的过程中会存在二次频率跌落的风险。
实际上,即使火电机组处于深度调峰状态,其也完全具备频率下扰工况下的一次调频响应能力,但只具备有限的频率上扰工况下的一次调频响应能力。以目前国内电力系统的配置情况及未来电力系统的规划,考虑到风电场的运行安全及效益,从电力系统频率安全的层面出发,风电场只需要具备在电力系统频率处于上扰工况时的快速降功率,以及在限功率运行方式下频率处于下扰工况时的快速升功率的能力,即可满足电力系统的调频需求。
目前,风电场运行的主流风电机组为变速风电机组(variable speed wind turbines,VSWT),其功率调节通过同时控制变流器和桨距角来实现,由于一次调频所要求的功率控制响应时间为秒级,而电力电子设备的响应时间为毫秒级,且变速风电机组的桨距角调节速率一般在3°/s~10°/s之间,因此在不限速的情况下,变速风电机组的功率调节速率完全可以满足上述要求。
鉴于此,本文通过建立含风电调频的电力系统频率响应模型,对制约风电场一次调频能力的非单机控制策略因素进行了逐一分析,并根据分析结果提出了风电场一次调频直控风电机组技术方案,深度挖掘了风电场一次调频能力,并在实际电力系统中进行了应用验证。
1 含风电调频的电力系统频率响应模型
电力系统具有高度非线性和时变性,与电压特性及功角特性相比,其频率响应时间尺度相对较慢。为分析负荷波动时的电力系统频率控制策略,忽略电力系统的快速动态变化(电压及功角变化)可以大幅降低建模的复杂程度,从而可以减小运算量和数据量。
1.1 电力系统模型
经典的电力系统频率响应模型如图1所示。其中:G代表常规电源发电单元(火电机组、水电机组、燃气发电电源);P*G为常规电源发电单元的输入指令;PG为常规电源发电单元的输出功率;PL为电力系统的有功功率需求;Ptie为与相邻电力系统联络线的交换功率;PRES为新能源发电系统的输出功率;PPFC为一次调频(primary frequency control,PFC)指令;PC为二次调频,即自动发电控制(automatic generation control,AGC)指令;R为常规电源发电单元的调差率;H为电力系统的惯性系数;D为电力系统的等效阻尼系数;s为拉普拉变换微分算子;Δf为电力系统的频率变化量。

图1 经典的电力系统频率响应模型Fig. 1 Classical power system frequency response model
当电力系统处于稳态时,其功率供需平衡,此时的关系可表达为:

1.2 常规电源发电单元及联络线功率模型
忽略动力源慢特性与发电机的快速动态特性,将调速器及原动机模型进行简化,并采用非线性环节,对发电机组出力速率及调速器死区进行模拟,得到的常规电源发电单元的简化模型如图2所示。图中:Tg为调速器的等效时间常数;Tt为原动机的等效时间常数;VL、VU分别为调速器阀门关闭速率的最大值和最小值。

图2 常规电源发电单元的简化模型Fig. 2 Simplified model of conventional power generation unit
电力系统区域间通过高压输电线路或联络线互联,每个区域的频率变化均会影响到与其互联的区域。在N个区域互联的电力系统中,区域i与其他区域之间联络线总交换功率变化量ΔPtie,i可表示为:
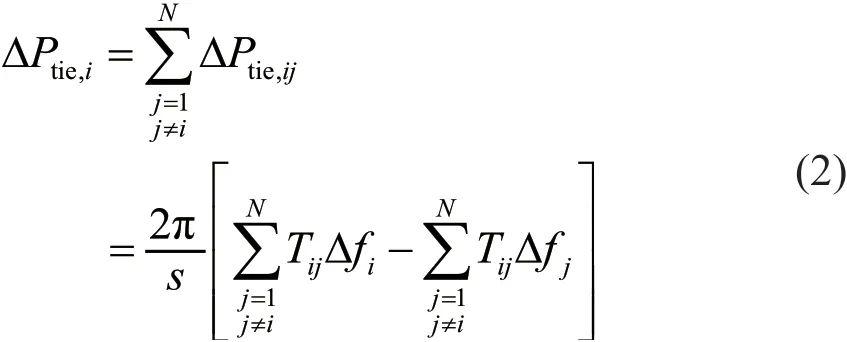
式中:ΔPtie,ij为区域i与区域j之间联络线的交换功率变化量;Tij为区域i与区域j的同步系数;Δfi、Δfj分别为区域i和区域j的频率变化量。
其中,Tij可表达为:

式中:Vi、Vj分别为区域i和区域j的等效机端电压;Xij为联络线的等效电抗分别为区域i和区域j在某平衡点处的等效发电机功角。
1.3 具有一次调频指令环节的变速风电机组风电场频率响应等值模型
目前主流风电机组为变速风电机组,分为全功率变换(full power converter,FPC)风电机组和双馈异步(doubly fed induction generator,DFIG)风电机组。FPC风电机组的工作原理图如图3所示,DFIG风电机组的工作原理图如图4所示。图中:TM为发电机的机械转矩;ω为发电机转速;PW为风功率;RSC为转子侧变流器;GSC为电网侧变流器;SSC为定子侧变流器;Pe为风电机组的有功功率;Vqs为定子侧q轴电压分量控制指令;Vqr为转子侧q轴电压分量控制指令。

图3 FPC风电机组的工作原理图Fig. 3 Working principle diagram of FPC wind turbine
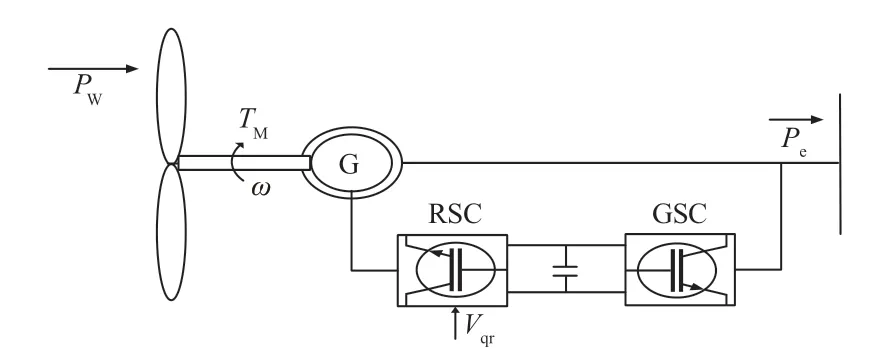
图4 DFIG风电机组的工作原理图Fig. 4 Working principle diagram of DFIG wind turbine
从图3可以看出,在FPC风电机组中,Pe通过控制Vqs来控制定子侧q轴电压分量进行改变。从图4可以看出,在DFIG风电机组中,Pe通过控制Vqr来控制转子侧q轴电压分量进行改变[15]。
基于上述分析,进行如下限定:1)忽略暂态因素及变流器损耗等因素;2)假设发电机输出的功率经过变流器后无任何延迟地传输至电力系统。
不同于常规电源发电单元,风电场中含有多台风电机组,因此为了便于研究,根据图3、图4所示的风电机组模型,采用“单机倍乘”的方式来代表风电场模型,并基于此模型,提出了具有一次调频指令环节的变速风电机组风电场频率响应等值模型,如图5所示。图中:PPFC,WT为风电场一次调频功率指令,输出功率指令直接作用于风电机组的功率控制回路;Pref,wt为针对风电机组的含有一次调频分量的功率指令;Vq、iq分别为DFIG风电机组的转子电压、转子电流的q轴分量;Vq′、iq′分别为FPC风电机组的定子电压、定子电流的q轴分量;kp、ki均为q轴电流PI控制器的参数;Te为发电机的电磁转矩;HW为风电机组的等效惯性常数;K1、K2、K3均为风电中部分环节的传函等效增益;T为风电中部分环节的时间常数。

图5 具有一次调频指令环节的变速风电机组风电场频率响应等值模型Fig. 5 Frequency response equivalent model of wind farm of VSWT with primary frequency control command link
具有一次调频指令环节的变速风电机组风电场频率响应等值模型可以模拟风电场一次调频频率上扰响应和限功率运行方式下频率下扰响应。
采用DFIG风电机组或FPC风电机组时,具有一次调频指令环节的变速风电机组风电场频率响应等值模型中K1、K2、K3、T的取值如表1所示。表中:Lm为磁化电感;Rr为转子电阻;Rs为定子电阻;Lrr为转子自感;Lss为定子自感;ωs为同步转速。
为简化表1中的计算,令:


表1 采用不同风电机组时模型中部分参数的取值Table 1 Values of some parameters in this model when different wind turbines are used
风电场一次调频指令环节模型如图6所示。该模型采用一阶惯性环节及非线性环节来表示一次调频指令实现的各个部分。图中:PPFC,wt为风电频率-有功下垂特性函数;fN为额定频率,取50 Hz,可以将频率测量环节向输出方向移动;Tmed为测频等效惯性时间;ra为一次调频功率指令的限速率;τ为一次调频功率指令的下发延迟时间;f为电力系统的频率;e为纯迟延环节的自然常数;Pwt为风电场一次调频功率指令;ΔPwt,m为第m台风电机组的一次调频功率分配指令;ΔPwt-ad为风电场的可调有功功率裕度;ΔPwt-ad,m为第m台风电机组的可调有功功率裕度;FM为频率测量环节;FCPC为一次调频功率指令计算环节;FCPD为一次调频功率指令的分配环节;FCPT为一次调频功率指令的下发延时环节;FCPSL为风电机组一次调频功率指令的限速环节。

图6 风电场一次调频指令环节模型Fig. 6 Model of primary frequency control command link of wind farm
为实现电力系统级的仿真,风电场一次调频指令环节模型是从风电场层面出发,而一次调频功率指令的分配环节的主要影响体现在响应时间上,所以采用一阶惯性环节进行近似替代,对风电场一次调频指令环节模型进行改进,如图7所示。图中:Tdis为一次调频功率指令分配的等效惯性时间。

图7 改进后的风电场一次调频指令环节模型Fig. 7 Improved model of primary frequency control command link of wind farm
由图5、图7可知,在控制对象不变时,即在风电机组单机控制架构及性能不发生变化的情况下,具有一次调频指令环节的变速风电机组风电场频率响应等值模型中影响风电场一次调频性能的参数主要包括Tmed、τ、Tdis、ra。
2 算例分析
2.1 算例介绍
为分析Tmed、τ、Tdis及ra对风电场一次调频能力的影响,以含1个风电场及9台常规电源发电单元的电力系统为例进行分析,该电力系统共分为3个区域,具体如图8所示。图中:PL1、PL2、PL3均为负荷。

图8 由1个风电场和9台常规电源发电单元构成的电力系统Fig. 8 Power system consisting of a wind farm and nine conventional power generation units
区域1中接入了1个1000 MW的风电场,该风电场包括500台2 MW的DFIG风电机组,风电渗透率为21%,风电场所在地平均风速为12 m/s,限功率深度为10%。常规电源调差率为5%,风电调差率为3%。9台常规电源发电单元的参数设置参考文献[16],DFIG风电机组参数的设置参考文献[15]。
2.2 仿真分析
结合现场实际情况,改变具有一次调频指令环节的变速风电机组风电场频率响应等值模型中参数Tmed、Tdis、τ、ra的数值,分析在相同扰动工况(200 s时区域1、区域2的负荷PL1、PL2同时减小0.05 pu的阶跃扰动量)下,不同参数值时风电场的一次调频性能及电力系统的频率响应情况。以区域1为例,具有一次调频指令环节的变速风电机组风电场频率响应等值模型的参数设置方案如表2所示,仿真结果如图9所示。图中:Δf1为区域1的频率变化量;ΔPwt为风电场实际功率增量。

表2 以区域1为例,具有一次调频指令环节的变速风电机组风电场频率响应等值模型的参数设置方案Table 2 Taking area 1 for example, parameter setting scheme of frequency response equivalent model of wind farm of VSWT with primary frequency control command link

图9 以区域1为例,不同参数值时的风电场一次调频性能及电力系统频率响应曲线Fig. 9 Taking area 1 for example,curves of primary frequency control performance of wind farm and frequency response of power system under different parameter values
以扰动工况下风电场响应滞后时间thx、响应时间t0.9、调节时间ts、调节精度Ac作为风电场一次调频性能的评价指标,以区域1的频率变化量极值ΔFpeak、稳定时间Trec、频率变化量终值ΔFfinal作为电力系统频率响应性能评价的指标。不同参数值时的风电场一次调频性能及电力系统频率响应结果如表3所示。其中:“方案0”为风电场不参与电力系统一次调频时的方案,其余方案编号与表2中相对应。

表3 不同参数值时风电场一次调频性能及电力系统频率响应的结果Table 3 Results of primary frequency control performance of wind farm and frequency response of power system under different parameter values
综合图9及表3中不同设置方案得到的结果,可以得到以下结论:
1)风电场参与电力系统一次调频后,相同扰动工况下ΔFpeak值及ΔFfinal值的绝对值均减小。
2)当风电场渗透率及调差率不变时,相同扰动工况下ΔFfinal值不变。
3)ΔFpeak值的降低,说明风电场一次调频性能得到了提升,电力系统的频率响应性能也相应得到了提高,缩短了电力系统频率波动的恢复时间。
4)参数ra的增加可以减小风电场一次调频的响应时间t0.9,从而减小ΔFpeak值。
5)参数τ的减小可以全面提升风电场一次调频性能,对电力系统频率响应性能的影响显著;τ越小,ΔFpeak值越小,Trec值越小,即电力系统的恢复时间越短。
6)参数Tdis、Tmed对风电场一次调频性能的影响程度相较于参数ra及τ而言较弱;Tdis、Tmed值越小,风电场一次调频的性能越好,ΔFpeak值也越小,Trec值越小,则电力系统的恢复时间越短。
3 风电场一次调频直控风电机组技术方案
3.1 风电场基础控制方案
根据上节研究内容可知,提升风电场一次调能力的关键在于提高ra值,减小Tmed、Tdis、τ值,尤其是τ值的减小。风电场有功功率控制架构如图10所示。

图10 风电场有功功率控制架构图Fig. 10 Block diagram of active power control of wind farm
从图10可以看出,调控中心下发有功功率指令需要通过远动装置至AGC系统,再经过交换机、通信管理装置下发至能量管理平台,然后再经过交换机下发至风电机组主控系统执行。此种方式的通信结构繁杂,设备层次繁多,有功功率指令下发延迟时间长,并且为了适应风电场有功功率变化最大限值的要求,对风电机组主控系统的有功功率变化率进行了人为限制。
一个设备的延时会影响整个通信网络的实时速率。通信管理装置往往是制约通信速率的瓶颈,由于该装置对下级设备需要采集大量信息,对上级设备需要与远动装置、AGC系统、自动电压控制(AVC)系统等通信,任务繁重,因此,为了降低成本,该装置的硬件配置通常较低,导致控制命令通过此装置的时间存在不确定性。另外,能量管理平台转发指令存在一定的延时,导致一条控制指令从调度到风电机组主控系统的周期时间为6~60 s,难以满足一次调频响应的要求。
3.2 风电场一次调频直控风电机组技术方案
目前风电场实现一次调频的技术方案主要有3种,即AGC系统改造方案、能量管理平台改造方案、单加调频控制系统方案。由图10可知,AGC系统改造方案和能量管理平台改造方案只可以在一定程度上减小τ值,但无法改变ra值;而单加调频控制系统方案目前主要通过一次调频指令下发至能量管理平台出口的形式来实现,但也只是进一步减小了τ值,仍无法改变ra值。
鉴于此,本文有针对性地提出了一种新的风电场一次调频直控风电机组技术方案,该技术方案的架构如图11所示。

图11 风电场一次调频直控风电机组技术方案的架构图Fig.11 Block diagram of technical scheme of primary frequency control and direct control wind turbine of wind farm
一次调频功率由调频控制系统通过调频交换机直接下发至每台风电机组主控系统,可最大限度地减小τ值,并对风电机组主控系统进行了升级,使其具备调频功率指令限速率切换控制功能。
3.3 风电机组主控系统调频功率指令限速率切换控制
为最大限度提升一次调频动作期间的ra值,在不影响风电机组原有控制性能的前提下,提出了风电机组主控系统调频功率指令限速率切换控制策略。该策略的功能框图如图12所示。图中:ΔPwt,i为第i台风电机组的一次调频功率分配指令;ΔPEMS,i为第i台风电机组接收的能量管理平台下发的有功功率指令。

图12 风电机组主控系统调频功率指令限速率切换控制功能的框图Fig. 12 Block diagram of frequency control power command speed limit rate switching control function of main control system of wind turbine
如果一次调频动作时,调频功率增量经过快速通道(ra=1.0 pu/min)执行;否则能量管理平台下发增量经过常规通道(ra=0.2 pu/min)执行,在不影响风电机组正常运行的同时,ra值得到了大幅提升。
3.4 一次调频功率的分配方式
一次调频功率的分配方式是否合理直接决定了Tdis值的大小,目前通常采用的一次调频功率分配方式为平均分配,如式(5)所示。

式中:ΔPwt(Δf)为一次调频的总有功功率;n为风电机组的台数。
为了最大程度地减小Tdis值,提出新的有功功率分配方式,如式(6)所示。

式中:ΔPwt-ad,i表示第i台风电机组的可调有功功率裕度。
新的一次调频有功功率分配方式可按照可调有功功率裕度百分比进行一次调频功率的分配,使一次调频功率分配更为科学、合理,尽量避免二次分配导致的Tdis值增加,且可以最大限度地减少风电机组快速响应的台数,相应地减少了风电机组桨距角的变化频次,有利于风电场中风电机组的使用寿命。
3.5 测频方法
Tmed值由测频装置具备的测频方法决定,测频原理如图13所示。图中:Ua、Ub、Uc为风电场并网点的三相电压。

图13 测频装置的测频原理框图Fig. 13 Block diagram of frequency measurement principle of frequency measurement device
目前,测频装置的频率计算环节可以实现1个周波内的高精度计算,保证Tmed值小于100 ms。
4 应用与实践
2020年6月,将本文提出的风电场一次调频直控风电机组技术方案在内蒙古电网中广核繁荣风电场进行了实际应用。该风电场的总装机容量为49.5 MW,由33台1.5 MW直驱式风电机组构成,加装了1套一次调频控制系统及调频交换机,利用原有的备用光纤网络实现调频控制系统与每台风电机组主控系统的通信,同时对每台风电机组主控系统及能量管理平台进行了升级改造,调频功率限幅设置为+6%PN(PN为风电场的额定功率)、-10%PN,死区为0.05 Hz,风电调差率为3%。通过各系统联调使该风电场具备了一次调频功能。利用电压频率变化信号源模拟风电场并网点电压互感器(PT)的二次侧信号,通过改变输出频率,检验风电场一次调频性能。频率阶跃下扰-0.14 Hz的实测与理论结果如图14所示,频率阶跃上扰+0.20 Hz的实测与理论结果如图15所示。图中:Pactual为实际功率;Ptheory为理论功率。

图14 频率阶跃下扰-0.14 Hz的实测与理论结果Fig. 14 Measured and theoretical results of frequency step down disturbance -0.14 Hz

图15 频率阶跃上扰+0.20 Hz的实测与理论结果Fig. 15 Measured and theoretical results of frequency step up disturbance +0.20 Hz
由图14可知,并网点初始功率为10.16 MW,当发生-0.14 Hz频率阶跃下扰时,并网点实际功率于0.35 s后开始响应一次调频,2.95 s后响应到位,实际功率为13.0 MW,响应调频功率为+2.84 MW,调频精度为0.32%。
由图15可知,并网点初始功率为12.38 MW,当发生+0.20 Hz频率阶跃上扰时,并网点实际功率于0.55 s后开始响应一次调频,2.25 s后响应到位,实际功率为7.08 MW,响应调频功率为-5.30 MW,调频精度为0.60%。
该风电场采用一次调频直控风电机组技术方案与采用常规调频技术方案的测试结果对比如表4所示。

表4 风电场一次调频直控风电机组技术方案与常规调频技术方案的测试结果对比Table 4 Comparison of test results between primary frequency control and direct control wind turbine of wind farm technical scheme and conventional frequency control technical scheme
从表4中各个表征调频性能的参数数值可以看出,相较于常规调频技术方案,风电场一次调频直控风电机组技术方案可以大幅提升风电场一次调频性能。
5 结论
针对电力系统对风电场一次调频性能的要求及风电场高效、低成本实现一次调频功能的需要,本文通过建立含风电调频的电力系统频率响应模型,对制约风电场一次调频能力的非单机控制策略因素进行了深度分析,有针对性地提出了风电场一次调频直控风电机组技术方案,并在实际电力系统中进行了实践应用。通过仿真及实测结果可以得到以下结论:
1)变速风电机组风电场在不对单机控制策略进行修改及优化的前提下,通过对测频、调频功率分配、调频功率下发、调频功率限速环节的优化完全可以高性能地实现电力系统要求的一次调频功能。
2)相对于单机控制策略优化的高成本和不可控等特征及常规调频技术方案的固有缺陷,采用风电场一次调频直控风电机组技术方案可以高性能、低成本地实现风电场一次调频功能,具有广泛的应用推广价值。
本文提出的风电场一次调频直控风电机组技术方案可为风电场低成本实现高性能一次调频功能提供借鉴思路。
