Investigation of stimulated Raman scattering in longitudinal magnetized plasma by theory and kinetic simulation

Hongyu ZHOU (周泓宇), Yan YIN (银燕), Kaiqiang PAN (潘凯强),Chengzhuo XIAO (肖成卓), Jinlong JIAO (矫金龙), Duan XIE (谢端),Tongpu YU (余同普),Fuqiu SHAO (邵福球) and Hongbin ZHUO (卓红斌)

1 Department of Physics, National University of Defense Technology, Changsha 410073, People’s Republic of China

2 Laser Fusion Research Center, China Academy of Engineering Physics, Mianyang 621900, People’s Republic of China

3 Key Laboratory for Micro-/Nano-Optoelectronic Devices of Ministry of Education & Hunan Province Key Laboratory of Low-Dimensional Structured Physics and Devices, School of Physics and Electronics,Hunan University, Changsha 410082, People’s Republic of China

4 Collaborative Innovation Center of IFSA (CICIFSA), Shanghai Jiao Tong University, Shanghai 200240,People’s Republic of China

5 School of Physics, Peking University, Beijing 100871, People’s Republic of China

6School of Electronic Information and Electrical Engineering, Changsha University, Changsha 410003,People’s Republic of China

7 Center for Advanced Material Diagnostic Technology, Shenzhen Technology University, Shenzhen 518118, People’s Republic of China

Abstract Stimulated Raman scattering(SRS)in a longitudinal magnetized plasma is studied by theoretical analysis and kinetic simulation.The linear growth rate derived via one-dimensional fluid theory shows the dependence on the plasma density,electron temperature,and magnetic field intensity.One-dimensional particle-in-cell simulations are carried out to examine the kinetic evolution of SRS under low magnetic intensity of ωc /ω 0 < 0.01.There are two density regions distinguished in which the absolute growth of enveloped electrostatic waves and spectrum present quite different characteristics.In a relatively low-density plasma (n e ~0.20nc), the plasma wave presents typical absolute growth and the magnetic field alleviates linear SRS.While in the plasma whose density is near the cut-off point (n e ~0.23nc), the magnetic field induces a spectral splitting of the backscattering and forward-scattering waves.It has been observed in simulations and verified by theoretical analysis.Due to this effect,the onset of reflectivity delays,and the plasma waves form high-frequency oscillation and periodic envelope structure.The split wavenumberΔk/ k0 is proportional to the magnetic field intensity and plasma density.These studies provide novel insight into the kinetic behavior of SRS in magnetized plasmas.

Keywords: laser plasma interaction, stimulated Raman scattering, longitudinal magnetized plasma, spectrum analysis, electron plasma wave

1.Introduction

In both the direct and indirect laser-driven inertial confinement fusion (ICF), laser plasma interactions present complex physical characteristics,including multiple wave-wave,waveparticle interactions[1–3].Parametric instabilities,such as the stimulated Raman scattering (SRS), the stimulated Brillouin scattering and some other decay modes, have an essential impact on the ignition of ICF [4–6].It is generally believed that parametric instabilities are important reasons hindering the ignition on the National Ignition Facility.In the instabilities,SRS receives a lot of attention,which is a typical decay process in plasma from an incident laser into a scattered light and an electron plasma wave(EPW)[7].This process leads to laser energy depletion by scattering light and capsule asymmetric compression by hot electrons preheating, which are both highly detrimental to the ignition process [8–10].

Therefore,many concerns have been paid to interpret the SRS mechanism and pursue methods to suppress the instability to a controllable stage [11–13].One kind of feasible method is to construct special laser fields to alleviate the instability, such as a broadband pump [14], a polarization smoothed pump [15] and a rotated polarized pump [16, 17],etc.The three-wave coupling in temporal space can be detuned by the specially designed pump, resulting in instability suppression.Another kind of method is to employ external longitudinal [18, 19] or transverse magnetic field[20, 21], which exploits Faraday rotational effect or hybrid wave modes to detune and alleviate the resonant coupling.The longitudinal magnetic field also rotates the polarized direction of pump when it propagates in plasma to suppress the instability, which is somewhat similar to the method of rotating polarized lasers.The difference is that the former one induces spatial decoupling, rather than temporal decoupling.Sukhdeep Kaur et al [22] and Z J Liu et al [23] respectively derived the linear theory of SRS immersed in a static longitudinal magnetic field by fluid theory and gave the numerical solution.Afterwards, K Q Pan et al [24] carried out the PIC simulation about the SRS driven by circularly polarized laser in strongly magnetized plasma.Previous works show that the magnetic field modifies the isotropic dielectric property and the refractive index of the plasma, consequently decoupling the instability spatially.For that reason,the external magnetic field is a very useful tool to control and alleviate SRS.However, more research is still needed to reveal the detailed kinetic characteristic of wave evolution and particle motion under the more feasible magnetic field, especially the growth mode and particle-trapping feature etc.

In this work,we use the fluid theory and kinetic simulations to investigate the SRS evolution in a static longitudinal magnetic field.Using the PIC code EPOCH[25],detailed simulations are carried out to focus on the kinetic characteristics of the instability.Besides the suppression effect, it is found that the spectrum appears an interesting splitting feature near the cut-off density of Raman scattering, which shapes the plasma waves into a periodic envelope and high-frequency oscillation.

This paper is organized as follows.In section 2,the linear growth of the stimulated Raman backscattering (SRBS) is theoretically analyzed in non-magnetized and magnetized plasma, respectively.In section 3, we introduce the parameters used in the long-term PIC simulations at first.Then,the characteristic of SRS in different density magnetized plasmasrespectively illustrated.Particularly, the impact of the density and magnetic field on spectral splitting is demonstrated via both theory and simulations.

2.Theoretical analysis of the linear SRBS

2.1.Linear SRBS in a non-magnetized plasma

Firstly,we use one-dimensional(1D)fluid fluctuation model to describe the three-wave coupling process to reexamine the linear temporal growth rate of SRBS without external magnetic field [7]:

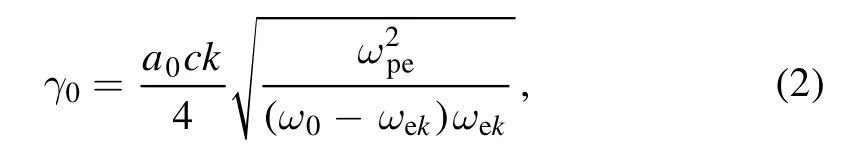
where the plasma wave frequency after thermal correction is.

Figure 1(a) shows the relations between the plasma density, the wavenumber (the left y-axis) and the frequency(the right y-axis) of each wave atTe=3 keV.The wavenumber of BSL and EPW both gradually decrease with the increase of plasma density.The former one approaches to 0 atne/nc=0.242,wherencis the critical density of the pump.It indicates that the BSL cannot propagate in the plasmas higher than this specific density,so that the cut-off density of SRBS is0.242nc.Figure 1(b) shows the dependence of normalized SRBS linear growth rate on the plasma density under different electron temperatures.Since the Landau damping cannot be ignored in the very low-density plasma and we just want to find the appropriate parameter space with the largest temporal growth rate,so that,we focus on the normalized density range from 0.10 to 0.25.At any specific electron temperature, the growth rate approaches to a peak value aroundne/nc≈0.20,then gradually decreases until the cut-off density.The growth rate and the cut-off density are inversely proportional to the electron temperature.It is shown that the growth rate remains large in the regionne/nc∊(0 .15, 0.25) ,so we make simulations in this density regime to study the magnetic effect in the following sections.

Figure 1.(a)Wavenumbers and frequencies of backscattered light(BSL)and EPW under different normalized plasma densities with electron temperature Te =3 keV.(b) The normalized growth rate of SRBS under different initial plasma densities and electron temperatures condition.The normalized plasma density ranges from 0.10 to 0.25.

2.2.Linear SRBS in a weakly magnetized plasma

In this section,we derive the linear growth rate of SRBS driven by a linear polarized pump with an external static longitudinal magnetic field.The magnetic feild,assumed as:will induce the Faraday rotational effect to rotate the polarization direction of a transverse wave when the wave propagates along the magnetic field.The rotating angle satisfies:

As we known, the dispersion equation of lasers in longitudinal magnetized plasma is:

the signs ‘+’ and ‘−’ in the denominator are for the LC and RC lasers, respectively, and normalized cyclotron frequency iswhere subscript 0, 1 respectively represents the pump and scattering light.In this paper, the range of the weak magnetic field we discussed satisfies0≤σ≤0.01,thus,we can obtain the dispersion equation of the SRBS in a magnetized plasma as follows [24]:

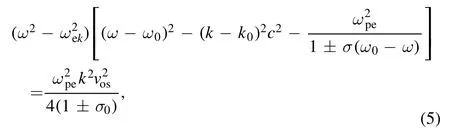
the signs ‘+’ and ‘−’ also represent the SRBS driven by LC and RC lasers.Taking theω=ωek+ iγ,considering the weak magnetic field condition and ignoring the high order terms, we could obtain the temporal growth rate of the EWP as:

where the subscript L represents the EPW driven by LC laser,and the magnetic effect term satisfies:

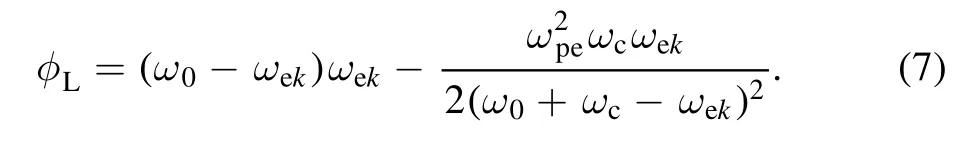
Though a bit complicated, the temporal growth rate of EPW driven by RC laser can be derived in the similarly method as:

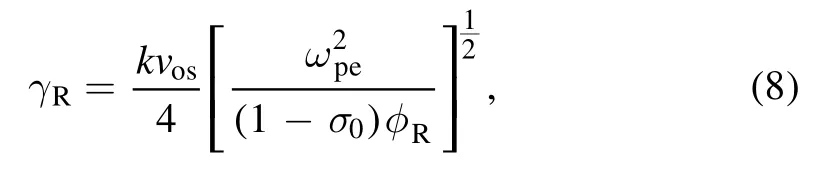
where the magnetic effect term is:

The formation of the equations (6) and (8) is alike.It is difficult to directly find the effect of the magnetic field on growth rate, however, when the external magnetic field approaches to zero,i.e.Bj→0,the equations(6)and(8)can return to the well-known results of equation (3).

Figure 2 shows the normalized theoretical temporal growth rate of the EPWs driven by LC and RC laser.Theγ0of each line is a variable, as shown in figure 1(b), which presents the temporal growth rate in non-magnetized plasma with the same density to that of magnetized plasma.Not as intuitive seems in the figure,indeed,the growth rate in0.24ncmagnetized plasma is larger than that in0.10ncmagnetized plasma, combined figures 1(b) and 2.Besides, in different density plasmas, the longitudinal magnetic field will suppress the growth of the SRBS driven by LC laser, as shown in figure 2(a), and meanwhile, enhance the growth rate of EPWs driven by RC laser.But it does not mean that the magnetic field has no suppression effect on the SRBS driven by the composed linearly polarized laser.Compared with figures 2(a)and (b),it can be seen that, when increasing the plasma density, the suppression effect on EPW driven by LC laser will be a bit more effective than enhancement effect on that of RC laser.Thus, the synthetic effect of the two lasers, i.e.the linearly polarized laser on SRBS is the suppression effect, and this effect is monotonically increasing with the intensity of magnetic field, which meets our expectations.Generally speaking,the coupling between EPWs excited by LC and RC pulse should be taken into account.However, the growth rate we derived is just for the linear stage.During this stage,the EPWs driven by LC and RC laser are both monochromatic, so the coupling of the SRS modes is very weak.Besides,the external magnetic field is weak in the parameter space of this paper,excluding other nonlinear effects.As a result, we can discuss the growth rate of EPWs independently.

Figure 2.The variation of the EPWs’ normalized temporal growth rate with cyclotron frequency driven by LC (a) and RC (b) laser in different density magnetized plasmas.

3.Simulation results and discussions

3.1.Simulation parameters

We carry out a series of 1D numerical simulations to explore the magnetized effect on linear SRS via EPOCH [25].We suppose the linear polarized pump propagating along x axis,and specify a static longitudinal magnetic field.The pump wavelength isλ0= 0.351 μm and the intensity is 2×1015W cm-2.The pulse duration is τ= 10000/ ω0.The plasma length is L = 300λ0.Its uniform density in the whole simulation box is chosen in the range n0∊(0 .15nc, 0.24nc),where the linear growth rate of SRBS is relatively large according to the fluid theoretical analysis.The electron temperature is Te=3 keV.Ions are supposed to be immobile in simulations, which provide a uniform, neutralizing background and artificially exclude Brillouin scattering.The total number of cells is 30 000 with 2048 electrons per cell.The absorbing boundary conditions are set for the electromagnetic fields.Hot electrons flowing out of the simulation box are replaced by the uniformly Maxwellian electrons as if the simulated plasma is in contact with a thermal plasma at the initial temperature.

3.2.SRS characteristics in a underdense magnetized plasma

Figure 3 shows the simulation results in a uniform plasma withne=0.20nc.Because the frequency drift of resonant point caused by the weak external magnetic field can be ignored, we simply use the three-wave coupling equations to obtain the wavenumber and frequency of each wave, i.e.k0=0.894ω0/c,k1=0.278ω0/c,k2=1.173ω0/c,ω1=0.527ω0,ω2= 0.473ω0.Meanwhile, the phase velocity of EPWφv equals to 0.4c and the threshold condition of absolute instabilityapproaches to0.04, where γpis the Landau damping rate, v1and v2are respectively the group velocities of the backscattered light and plasma wave[26].For the B= 0 T case as shown in figure 3(a), the background noise gradually grows to the notable backscatter and propagates from right to left boundary.The onset time of instantaneous reflectivity is about2100/ω0, then the backscatter reaches the peak before3100/ω.0Figure 3(b) shows the envelopes of the electrostatic wave in linear stage with a time interval 30τ =60π /ω0from nearly2100/ω0to 2800/ ω0,whereτ is the laser period.Here,we use the Hilbert transformation to obtain the EPW envelope.Since the criterion β < 2, the EPW absolutely grows in the coupling region, as shown obviously between0 ~70λ0,demonstrating a typical absolute gain that the electric field of each point simultaneously increases.In figure 3(c),the high boundary of electrons momentum begins to expand from linear stage 0.4mec to nonlinear stage 0.8mec due to the particle-trapping.Dung this time,the distribution gradually forms a flat-top and finally varies to a convex-top around0.6mec after saturation(~480τ).In all cases, the instability is driven by a linear zpolarized pump, accompanied with the static magnetic field whose intensity gradually raises from0 T up to200 T.Meanwhile, the Faraday rotational effect validates more visibly.As the polarization direction rotates faster, the ycomponent of pump energy becomes larger.Consequently,the backscatter in y-direction is excited more violently.Therefore, the difference betweenI-andis gradually increasing from figures 3(d) to (g).Besides, a smaller zcomponent of pump energy decreases the growth rate and delays the onset and saturation time of reflectivity respectively to2200/ω0and3200/ω.0The peak reflectivity maintains stable since the total pump energy does not change.Then,the absolute growth rate of EPW decreases as the wave packet peak at450τdeclines to 0.7 × 1011V m-1as shown in figure 3(h).On the contrary,the length of the first absolute growing packet raises to about150λ0.Due to the relatively large phase velocity in this density plasma, particle-trapping effect remains weak during the simulation time, so that the momentum and the number of hot electrons both reduce a bit while enhancing magnetic field from figures 3(c) to (i).However, the above phenomena illustrate that an external longitudinal magnetic field helps alleviate the linear SRBS and thus changes evolution characteristics.

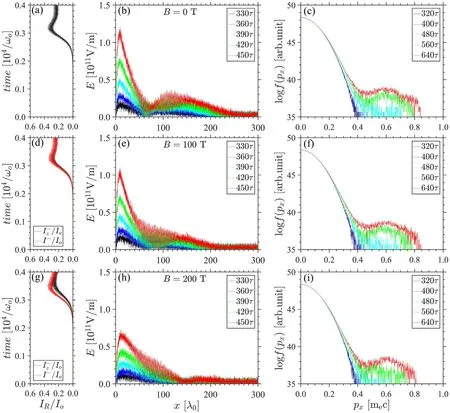
Figure 3.(a),(d), (g)The normalized instantaneous reflectivities of the cases B =0 T,100 T and200 T,respectively, where black and red lines respectively represent the z-components and the total reflectivity.(b),(e),(h)The envelopes of the longitudinal electric field in the linear stage.(c), (f), (i) The electron momentum distributions varying from linear stage to nonlinear stage.All the simulated results are obtained under the plasma density ne =0.20nc and the three figures in each row are for the same case.

3.3.Impact of the density and magnetic field on spectral splitting

Besides the spatial-temporal evolutions of waves and particles, the magnetic field effect on SRS is also revealed in the spectral space.Figure 4 shows the frequency-wavenumber space of EPWs under different parameters during the linear stage.In figures 4(a)–(d), the plasma density is fixed asne=0.23ncwhile the external magnetic field evenly increases from0 T to300 T.In figures 4(e)–(h), the external magnetic field is fixed asB= 300 T while the plasma density gradually increases.The spatial-temporal period for spectral analysis is the same for each case.Figures 4(a)–(d) show the two significant signals in the linear stage of each case:the left one is the resonant point of the stimulated Raman forward scattering (SRFS) and the right one is for SRBS.With the increasing magnetic field strength, both SRBS and SRFS become weaker in the linear stage.Meanwhile,each resonant mode’s signal gradually splits into two comparable signals with a small differenceΔk/k0,which is positively related to magnetic field amplitude.In figures 4(e)–(h),with a specified magnetic fieldB= 300 T, the spectral splitting is shown proportional to the plasma density.Due to the resolution limitations,we could just measure theΔkof the SRBS in the figures 4(c), (d), (g), (h), which are about0.023k0,0.030k0,0.022k0,0.044k0,respectively.TheΔkof the SRFS can be a pproximately treated equally to the SRBS.

Figure 4.(a)–(d) Frequency-wavenumber space of EPWs under different external magnetic fields at ne =0.23n c.(e)–(h) Frequencywavenumber space of EPWs under different plasma densities at B =300 T.All of the Fourier-transforms are during the linear stage of SRS.

Here, we first qualitatively interpret the spectral splitting phenomenon.When deriving the linear growth rate of SRS without an external magnetic field, we could obtain the dispersion relation from equation (1) as follows:

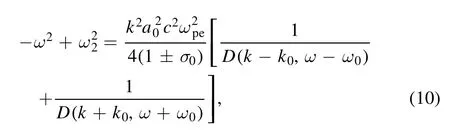
where the sign ‘±’ respectively represents the dispersion process of the LC and RC laser in plasma,D(k-k0,ω-ω0)=(ω-ω0)2- (k-k0)2c2-/1±σ(ω0-ω)represents the down shifted light wave andD(k+k0,ω+ω0)=(ω+ω0)2- (k+k0)2c2-/1±σ(ω0+ω)represents the up shifted one,the sign‘±’in these two equations has the same meaning as above.

Thus,when we stimulate SRS by a linear polarized laser in the longitudinal magnetic plasma, this process indeed stimulates four circularly polarized scatterings: two down shifted light waves with a bit different wavenumbers are for SRBS process, while two up shifted light waves with a bit different wavenumbers are for the SRFS process.In order to show the four-wave coexistence characteristics more clearly,we can first ignore the rotating effect of the scattered light,and rewrite the coupling equation into the following form:

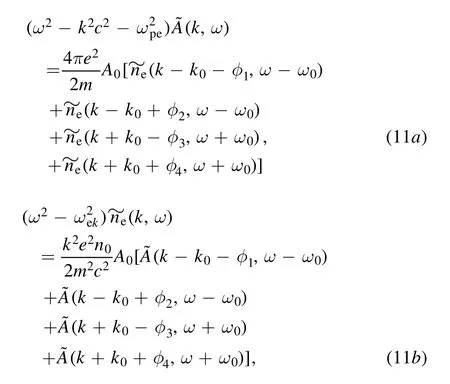
whereφ1toφ4respectively represent the absolute values of EPW wavenumbers splitting in the SRBS and SRFS.It is obviously that the SRS excites four plasma waves with different wavenumbers.Next,we take the SRBS process as an example to illustrate the phenomenon of spectral splitting.

When we derive the maximum temporal growth rate,the scattered light should be also resonant at the same time, i.e.

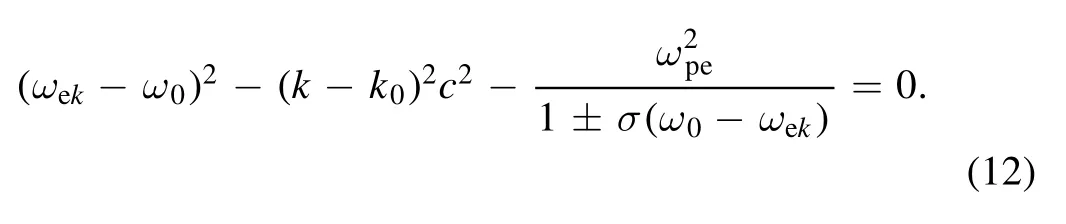
For the LC laser, the sign takes ‘+’ and the growth rate reaches maximum when the scatter directly backward propagates, i.e.

where the eigenvalue ofk0should be:

Similar to the above result, the maximum wave vector of EPW driven by right-handed circularly polarized laser is:

Then, we could utilize equations (9) and (10) to obtain the wavenumber difference of two circularly polarized laser as:

From the above, we can find that the wavenumber difference is positive related to the plasma density and the external magnetic field.When under the very weak magnetic field or in the very low-density plasma, i.e.ωc→0orne→0,the EPW wavenumber difference will also approach to zero,which means the disappearance of the spectral splitting effect.

Figure 5 shows the comparison between the theory and simulation values of the normalizedΔk in different parameter spaces.The blue lines are corresponding to the results of the equation (16), respectively take the magnetic field strength and plasma density as independent variable.TheΔk is proportional to the first power of the magnetic field and positive related to the high power of the plasma density.It can be seen from the figure that the theoretical value and the simulated value are in well agreement within the measurable range.Thus, we could conclude that, when the plasma density rises comparable to the cut-off density (ne>0.23nc) or the magnetic field is larger than200 T (ωc~ 0.01ω0), the magnetic modulation effect becomes visible, the original two resonance points of SRFS and SRBS split into four highlight signals.In contrast, there is no visible splitting in the lowdensity and magnetized plasma.

Figure 5.The normalized Δk of EPWs in SRBS under different density and magnetized plasmas, the blue lines represent the theory value while the red crosses are for the simulation results.

3.4.SRS characteristic in a magnetized plasma near cut-off density

In figure 3, the intensity of SRFS and the splitting effect are both weak because the plasma density is relatively smaller than the cut-off density,and the evolution of SRBS is mainly affected by the external magnetic field.In the following part,we will focus on the case near the cut-off density point where some phenomena different from figure 3 could be observed.Figure 6 shows the normalized instantaneous reflectivity, the envelopes of the longitudinal field, and the electron energy distributions under different magnetic fields with the plasma densityne=0.23nc.It is shown in figure 4 that the spectral splitting cannot be ignored in the cases with ne=0.23nc.The wavenumbers and frequencies of each fundamental wave in this case are respectively k0=0.877ω0/c,k1=0.147ω0/c,k2=1.025ω0/c,ω1= 0.502ω0, ω2= 0.498ω0,and the threshold condition of absolute instability β is 1.1 × 10-4.In the B= 0 T case, as shown in figure 6(a), the onset time of reflectivity slightly delays to2200/ω0and the saturation level is still about0.4 as same as that in previous cases.However,the performance of EPW varies much.Firstly, the largest growth rate point alters fromx =10λ0tox =75λ0.Secondly, the envelope violently fluctuates, which can be attributed to the beat of SRFS and SRBS.In figure 4(a), the wavenumber difference of two signals isΔ k≈0.4k0.Therefore, the wavelength of the beat pattern is equal to λ0/0.4 =2.5λ0,which coincides with figure 6(b).Apart from the difference, the growth rate of EPW does not change much.The peak value at450τ is still about 1.1 × 1011V m-1and the particle-trapping also remains weak while the phase velocity approaches to0.5c .When raising the magnetic field intensity, the onset time of reflectivity gradually delays to 3000/ ω0due to the alleviation effect in the linear stage.Because of the competition between SRBS and SRFS, the saturation value of the reflectivity also decreases, leading to the decline of SRBS proportion.Besides,from figures 6(e)to(h), the periodic characteristics of EPW envelope become more obvious with the typical beat pattern between the splitting waves of SRBS.In figure 4(d), theΔk of the split SRBS waves is about0.03k0, which means a synthetic envelope with wavenumber λ = λ0/0.03 =33.3λ0as that in figure 6(h).Obviously, EPW takes longer time to grow up to the intense peak around 1.1 × 1011V m-1, even though the electron energy decreases with the increase of magnetic field,the change of the distribution is still little because the particletrapping effect is weak.

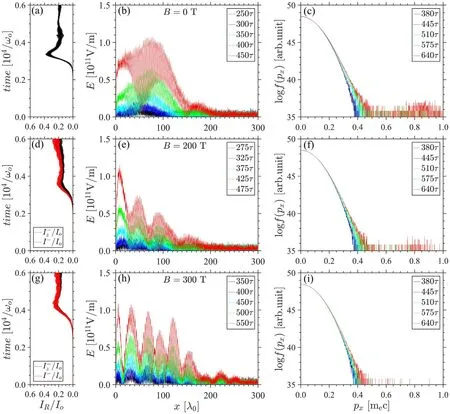
Figure 6.(a), (d), (g) The normalized instantaneous reflectivities of the cases B =0 T,200 T and300 T, respectively, where black and red lines respectively represent the z-components and the total reflectivity.(b),(e),(h)The envelopes of the longitudinal electric field in the linear stage.(c), (f), (i) The electron momentum distributions varying from linear stage to nonlinear stage.All the simulated results are obtained with the plasma density ne =0.23n c.The three figures in each row are for the same case.

In all, the above simulations show that, regardless of the plasma density,the alleviation effect of longitudinal magnetic field on linear SRS is always valid.The Faraday rotational effect rotates the laser polarization in propagation and leads to the three-wave coupling state continuously changing in space,which is the expected spatial decoupling.The SRS driven by linearly polarized laser is indeed stimulated by a LC laser and a RC laser with a frequency difference.Under relatively large magnetic field near the cut-off density,the two growth modes of LC and RC with different wavenumbers form the spectrum splitting phenomenon, causing the changes of evolution characteristics and the competition between SRFS and SRBS.We attribute this process to the variety of the dielectric property and the refractive index of plasma induced by the external magnetic field.

4.Conclusions

The effect of external longitudinal magnetic field on the linear SRS is studied via fluid theoretical analysis and kinetic simulation.The growth rate of SRBS, which is derived by simple fluid theory,shows dependence on the plasma density, electron temperature and magnetic field intensity.We carry out a series of 1D PIC simulations to intuitively reveal the kinetic evolution characteristics.When the magnetic feild satisfeisωc/ω0< 0.01 and the uniform plasma density is belowne≤0.20nc,the absolute growth is alleviated, and the particle-trapping effect maintains weak.For a uniform plasma withne≥0.23nc,the SRFS cannot be ignored.Our theoretical analysis and PIC simulations both present the spectral splitting of SRFS and SRBS, and the split wavenumber is positively related to the magnetic field intensity and the plasma density.Besides the alleviation effect, the beat of split waves declines the saturation of reflectivity and makes the EPW envelope present a prominent periodic structure and high-frequency fluctuations.The modulation effect of magnetic field on SRS characteristics becomes more significant near cut-off density.From the whole simulation results, it seems that weak longitudinal magnetic field is not appropriate to suppress the SRS process in deep nonlinear stage,as the reflectivity and hot electrons’ energy tend to be steady after saturation.If we want to suppress SRS for a longer time,we need to strengthen or make a special configuration of the magnetic field.However,SRS in the weakly magnetized plasma exhibits some new phenomena that we have not expected,which helps us to reveal the physical mechanism of instability evolution.The above analysis validates in the parameters spaceI0~1015W cm-2,ωc/ω0< 0.01,where other complex nonlinear evolutions of plasma wave and electrons induced by ultraintense laser and external magnetic field are excluded.

Acknowledgments

This work is supported by the National Key Research and Development Program of China(No.2016YFA0401100),the Strategic Priority Re-search Program of Chinese Academy of Sciences (No.XDA25050700), the Scientific Research Foundation of Hunan Provincial Education Department (No.20A042), and National Natural Science Foundation of China(Nos.11805062, 11675264, 11774430).