毫米波大规模MIMO-NOMA系统中基于动态子连接混合结构的预编码设计
2021-11-29景小荣张思思
景小荣, 张思思
(1. 重庆邮电大学通信与信息工程学院, 重庆 400065;2. 移动通信技术重庆市重点实验室, 重庆 400065)
0 引 言
当前,6 GHz以下的蜂窝频谱严重不足,而毫米波频段可利用的频谱资源却非常丰富,但易受路径等衰落的影响[1]。大规模多输入多输出(massive multiple input multiple output,mMIMO)技术通过利用基站(base station,BS)部署成百上千根天线所带来的巨大阵列增益,恰好可弥补毫米波信号在传输过程中所承受的严重路径损耗[2]。因此,毫米波与mMIMO相结合,即毫米波mMIMO,使系统容量得到显著提升。同时,与正交多址接入(orthogonal multiple access,OMA)不同,功率域非OMA(non-OMA, NOMA)利用叠加编码和连续干扰消除(successive interference cancellation,SIC)技术[3],在有限的资源里为更多的用户提供服务,以实现大规模连接和低延迟传输,将进一步提升系统频谱效率。因此,毫米波mMIMO和NOMA技术的融合,将为未来移动通信更高频谱效率的需求提供强有力的保障。
众所周知,在传统MIMO系统中,为降低接收机设计复杂度,通常基于全数字结构(full digital architecture,FD-A)对发射信号进行预编码处理[4],BS端需为每根天线配备专用的射频(radio frequency,RF)链。毫米波mMIMO系统中BS端通常配备数百根甚至上千根天线,若继续沿用FD-A,将导致无法承受的硬件成本和系统功耗。为此,学术界提出基于混合结构(hybrid architecture,HA)的预编码[5]设计思路,即将预编码分解为数字预编码器和模拟预编码器两部分,该结构仅需少量RF链,同时模拟预编码器可采用低成本的模拟移相器(analog phase shifters,APS)来实现,从而大幅度地降低了系统硬件成本和功耗。
截止目前,针对毫米波mMIMO系统,已有大量文献基于HA,设计了许多预编码方案。按照RF链和发射天线之间的连接方式,现有HA可分为全连接HA(fully-connected HA, FC-HA)和子连接HA(sub-connected HA, SC-HA)。基于FC-HA,文献[6]将混合预编码器和组合器联合优化问题分解为两个独立的优化问题,进而利用迭代算法求取次优解。解培中等人针对信号传播漫散射而造成的用户间干扰问题,提出一种基于SIC的鲁棒预编码器设计方案[7]。文献[8]在对基带预编码矩阵分解基础上,将预编码设计映射成一多层神经网络来实现。文献[9]以最大化系统能效为目的,提出一种次优迭代算法来设计预编码矩阵。尽管基于FC-HA的预编码设计方案具有相对优越的性能,但其所需APS的数量是发射天线的数量与RF链数量的乘积。同时,其还需与发射天线数相等的加法器,这意味着基于FC-HA的预编码设计方案的硬件成本和功耗依然很高。
在SC-HA中,每个RF链仅与发射天线的某一固定子集相连,有效地减少了系统对APS的需求。同时,在多用户系统中,所需RF链的数目可设定与用户数相当。于是,其系统功耗和硬件成本均得到大幅度降低。因此,SC-HA更适用于实际系统。基于SC-HA,文献[10]提出一种基于SIC的混合预编码器设计方案,相比于文献[7],该方案避免了奇异值分解和矩阵转换。然而传统的SC-HA不够灵活,因此文献[11]通过动态改变RF链和天线之间的连接方式,提出一种基于动态SC-HA(dynamically SC-HA, DSC-HA)的预编码方案。与FC-HA和SC-HA相比,该方案在降低系统功耗的同时,系统频谱效率得到明显提升。
随着无线通信的发展,面对5G频谱效率提升5~15倍的需求,NOMA由于具备良好的过载特性而逐步引起人们的关注。于是,部分学者提出将毫米波mMIMO和NOMA相结合,形成毫米波mMIMO-NOMA系统,并对其预编码技术展开深入研究。文献[12]针对FC-HA,以最大化系统和速率为目标,提出了基于有限反馈波束码本的预编码设计方案,进而通过用户配对和功率分配算法来减小NOMA用户簇内和簇间干扰。文献[13]提出一种基于联盟博弈论的用户分组和天线分配算法,以获得模拟波束赋形矩阵,进而利用低复杂度线性预编码算法设计数字预编码矩阵。Dai等人以最大化系统可达速率为目标,构建一有关预编码与功率分配的联合非凸优化问题[14],进而提出一种簇头选择算法来实现模拟预编码设计,并根据等效信道来设计数字预编码矩阵。在文献[14]的基础上,文献[15]提出一种相对比较复杂的模数预编码和功率分配联合设计方案。总之,目前针对毫米波mMIMO-NOMA系统中混合预编码技术的研究处于起始阶段,而且这些研究均基于FC-HA。因此,对于毫米波mMIMO-NOMA系统而言,这将会引起非常高的硬件成本和功耗。
在上述分析基础上,本文针对毫米波mMIMO-NOMA系统,基于DSC-HA,提出一种高效预编码方案。在该方案中,在对用户进行分簇的基础上,基于等效信道增益最大化原则利用KM算法来实现DSC网络设计,即发射天线动态分组,进而实现模拟预编码矩阵设计,以实现RF链与发射天线间的动态匹配。在此基础上,采用迫零(zero forcing,ZF)算法实现数字预编码器设计,以达到消除簇间干扰的目的。最后,以最大化各NOMA簇和速率为目标,对簇内用户功率进行分配,以减小簇内用户间干扰。仿真结果表明,本文针对毫米波mMIMO-NOMA系统提出的基于DSC-HA的预编码方案的系统和速率不但明显优于基于SC-HA的预编码方案,而且能效显著优于基于FD-A和FC-HA的预编码方案。
1 系统模型
考虑如图1所示的多用户毫米波mMIMO-NOMA系统下行链路。假设BS配置N根天线和M(M≪N)个RF链,为K(K≥2M)个单天线用户提供服务。为了充分实现多路复用增益,假设数据流数等于RF链数。为便于后续分析,将BS配置的N根发射天线依次用1,2,…,N标记,并以集合Ψ={1,2,…,N}表示。M个RF链依次用1,2,…,M标记,并以集合Θ={1,2,…,M}表示。根据文献[16],从K个用户中选择2M个用户,分别用1,2,…,2M标记,以集合U={1,2,…,2M}表示。进一步,对其进行分簇,假设每个NOMA簇最多容纳两个用户。
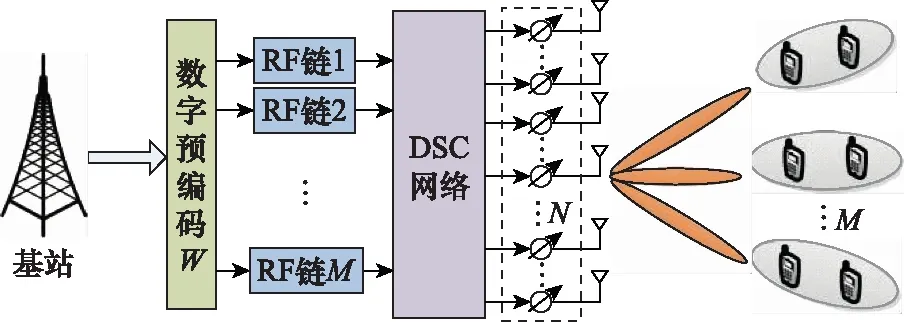
图1 动态子连接混合结构系统模型Fig.1 Dynamically sub-connected hybrid architecture system model
基于上述条件,第m个NOMA簇内强用户的接收信号为
(1)
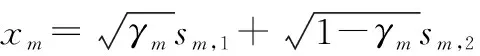
与文献[17]类似,采用基于扩展的Saleh-Valenzuela模型对毫米波信道进行建模,则
(2)
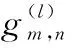
(3)
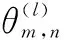
2 问题提出
假设各NOMA簇内强用户采用理想SIC,即完全消除簇内弱用户干扰,则第m个NOMA簇内强用户的接收信号可简化为
(4)
对应地,接收信干噪比为
(5)
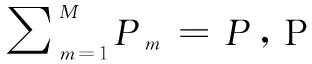
根据NOMA功率分配原则,弱用户无法利用理想SIC消除来自强用户的干扰,故第m个NOMA簇内弱用户接收信号为
(6)
对应地,接收信干噪比为
SINRm,2=
(7)
根据式(5)和式(7),系统可达和速率为
(8)
式中:Rm,n=log2(1+SINRm,n)(m=1,2,…,M;n=1,2)。
以系统可达和速率最大化为目标,预编码设计问题则等效为下列优化问题:
C2:‖Fwm‖2=1,m=1,2,…,M
(9)
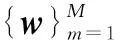
3 基于DSC-HA的预编码设计
在预编码设计过程中,先假设系统中用户均采用相同发射功率,并在忽略NOMA簇间和簇内干扰的条件下,利用用户信道状态信息的差异性,结合KM算法完成发射天线动态分组,进而实现模拟预编码矩阵设计。接着,以模拟预编码后的等效信道为基础,实现数字预编码矩阵设计。最后,以最大化各NOMA簇和速率为目标,通过优化簇内各用户功率分配,来降低簇内用户间干扰。下面分别对其进行说明。
3.1 动态天线分组和模拟预编码矩阵设计
依照上述设计思路,当所有用户采用相同的发射功率,式(9)中目标函数可展开为
(10)
式中:
式(10)要取得最大值,只需对于任意NOMA簇m,使Gm(F)取得最大值即可。这意味着对于不同NOMA簇,将存在不同的模拟预编码矩阵Fm,其中1≤m≤M,这显然与实际情况不符。根据前述分析,系统中所有NOMA簇必须共用同一模拟预编码矩阵F。于是,将F分成M列,其中第m列与第m个NOMA簇相匹配,这样同时也保证了各NOMA簇的公平性。即使如此,根据Gm(F)的结构,优化问题式(9)仍不易求解。
为使该问题可解,令暂时忽略簇间干扰(即先不考虑数字预编码)和簇内强用户对弱用户的影响,则优化问题式(9)转化为关于发射天线动态分组与模拟预编码设计的联合优化问题:
C3:Am∩Am′=φ,m≠m′
(11)
式中:
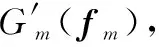
C3:Am∩Am′=∅,m≠m′
(12)
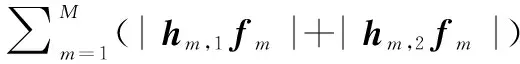
为各RF链选择最佳连接天线的问题,本质上可等效为一加权二分图最佳匹配问题,而KM算法[18]被证明是求解这类问题的一种有效手段,因此文中采用KM算法来解决天线分组问题。
为了降低天线分组的复杂度[11],同时保证各NOMA簇的公平性,令每个RF链均与N/M根天线相连。在该条件下,下面给出发射天线分组的流程,可分4个阶段实现,具体步骤如下。
步骤 1初始化阶段
为所有RF链和发射天线构成的集合Θ和Ψ中每一个顶点赋予一标号,记作可行顶标,分别用L(m)和L(p)表示,m∈Θ,p∈Ψ。相应地,由集合Θ和Ψ中任意两顶点m和p构成的边称为可行边,即e=(m,p),边权值用w(m,p)表示。天线分组中,每一次天线选择,集合Θ和Ψ中顶点的可行顶标分别初始化:
(13)
式中:hm,1,p和hm,2,p分别为第m个NOMA簇中强和弱用户信道矢量的第p个元素,m=1,2,…,M,p=1,2,…,N。
步骤 2天线循环选择阶段
对集合Θ中顶点m,从集合Ψ中选择使边权值w(m,p)=|hm,1,p|+|hm,2,p|最大的顶点pm与之匹配。由于集合Θ中每个顶点在集合Ψ中选择使边权值最大的顶点时,均从集合Ψ的N个顶点中选择。而根据前述优化分析,每根天线仅与一个RF链相连。因此,需判断集合Ψ中顶点是否与集合Θ中顶点存在一对多重复匹配。如果不存在,即经一次循环,集合Θ中各顶点分别与集合Ψ中M个不同顶点实现匹配,文中称作最佳匹配,则将匹配天线索引pm放入与第m个RF链对应的天线集合Am中,其中m=1,2,…,M;否则进入匹配更新阶段。
步骤 3匹配更新阶段
对于集合Ψ中顶点与集合Θ中某些顶点(为便于后续描述,令由这些顶点组成子集Ξ⊆Θ)存在一对多匹配时。令集合Ψ中该顶点与Ξ中序号最小的顶点ζmin相匹配,而对Ξ中其他顶点,依序利用深度优先遍历(depth first search, DFS)方法[19]从集合Ψ中剩余的未与集合Θ中顶点相匹配的顶点(令由这些顶点组成子集Π⊆Ψ)中寻找使得边权值最大的顶点,即判断是否存在可行边。若存在,将当前顶点m′∈Ξζmin与子集Π中该顶点相匹配;否则修改当前顶点的可行顶标。为此,引入变量:
d=min{L(m′)+L(p′)-w(m′,p′)}
(14)
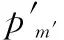
步骤 4信道更新阶段
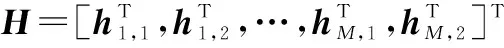
在上述发射天线分组的基础上,根据各RF链连接的天线集设计对应的模拟预编码矢量。考虑到实际系统中APS分辨率通常有限,假设设定APS分辨率为Bbits,则fm中第p个元素可表示为
(15)
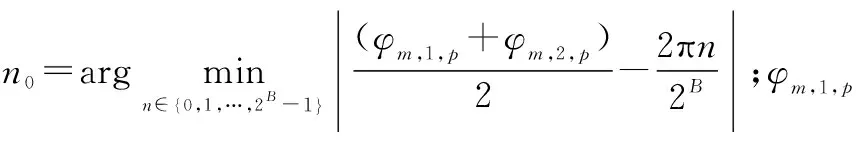
3.2 数字预编码矩阵设计
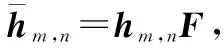
(16)
最后,对W进行归一化处理以满足功率约束条件,则第m个NOMA用户簇的数字预编码矢量为
3.3 功率分配因子优化
经预编码处理,各NOMA簇间干扰已被有效削弱;然而,在上述设计过程中,为简化分析,假设所有NOMA簇均采用相同发射功率[20]。因此,本节将通过优化簇内用户间功率分配,来减小簇内用户间干扰。
考虑NOMA簇内功率分配时,为了最大化各NOMA和速率,构建如下优化问题:
s.t. C1:0<γm<1
(17)
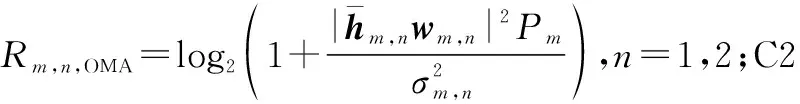
显然,优化问题式(17)为受限条件下关于γm的单变量优化问题,其中C4可等价为
(18)
令
则βm,1≥βm,2。
利用式(5)和式(7),式(17)中Rm,1和Rm,2可表示为
(19)
在此基础上,对C2和C3进行化简,可得功率分配因子γm的取值范围:
γm∈[γmin,γmax]=
(20)
至此,优化问题式(17)已化简为无约束的单变量求最值问题。将式(19)代入式(17),对其关于γm求一阶导:
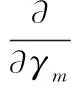
(21)
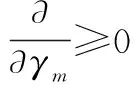
(22)
综上,基于DSC-HA的预编码设计步骤如下所示。其中,步骤1实现动态天线分组;根据发射天线动态分组的子集,步骤2~步骤7实现每个RF链对应模拟预编码矢量设计;步骤8~步骤11确定系统中强用户的等效信道;步骤12~步骤15实现数字预编码设计;步骤16~步骤22对各NOMA簇内用户进行功率分配。

输入:下行链路信道矩阵H,APS分辨率B初始化:F=0,H=0,Am=⌀,γm=0(m=1,2,…,M)步骤 1 由KM算法完成天线分组,得到天线集合{Am}Mm=1;步骤 2 for m=1,2,…,M步骤 3 for p=1,2,…,N步骤 4 if p∈Am步骤 5 n0=argminn∈{0,1,…,2B-1}(φm,1,p+φm,2,p)2-2πn2B;步骤 6 fm,p=e-j2πn02B;步骤 7 end if end for end for步骤 8 for m=1:M;步骤 9 hm,1=hm,1F;步骤 10 end for步骤 11 H=[hT1,1,hT2,1,…,hTM,1]T;步骤 12 利用式(16),确定W;步骤 13 for m=1:M步骤 14 wm=wm‖Fwm‖2;步骤 15 end for步骤 16 for m=1:M步骤 17 利用式(22),确定γm=γ*m;步骤 18 if γm∈(0,1)步骤 19 γm=γ*m;步骤 20 else步骤 21 γm=Pm;步骤 22 end if end for输出:F,{wm}Mm=1,{Am}Mm=1,{γm}Mm=1
3.4 计算复杂度
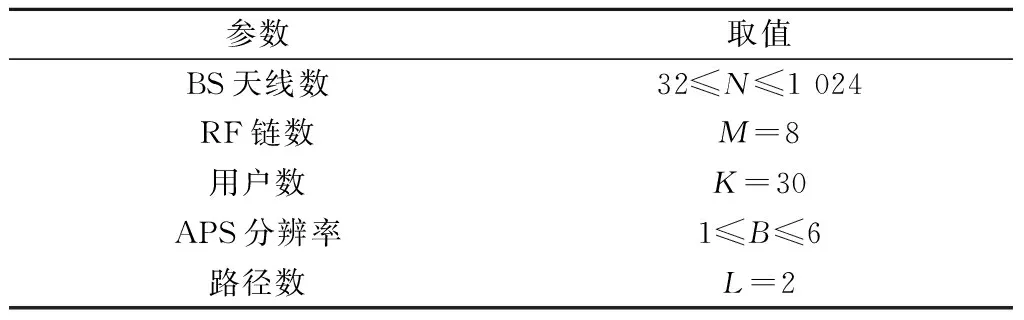
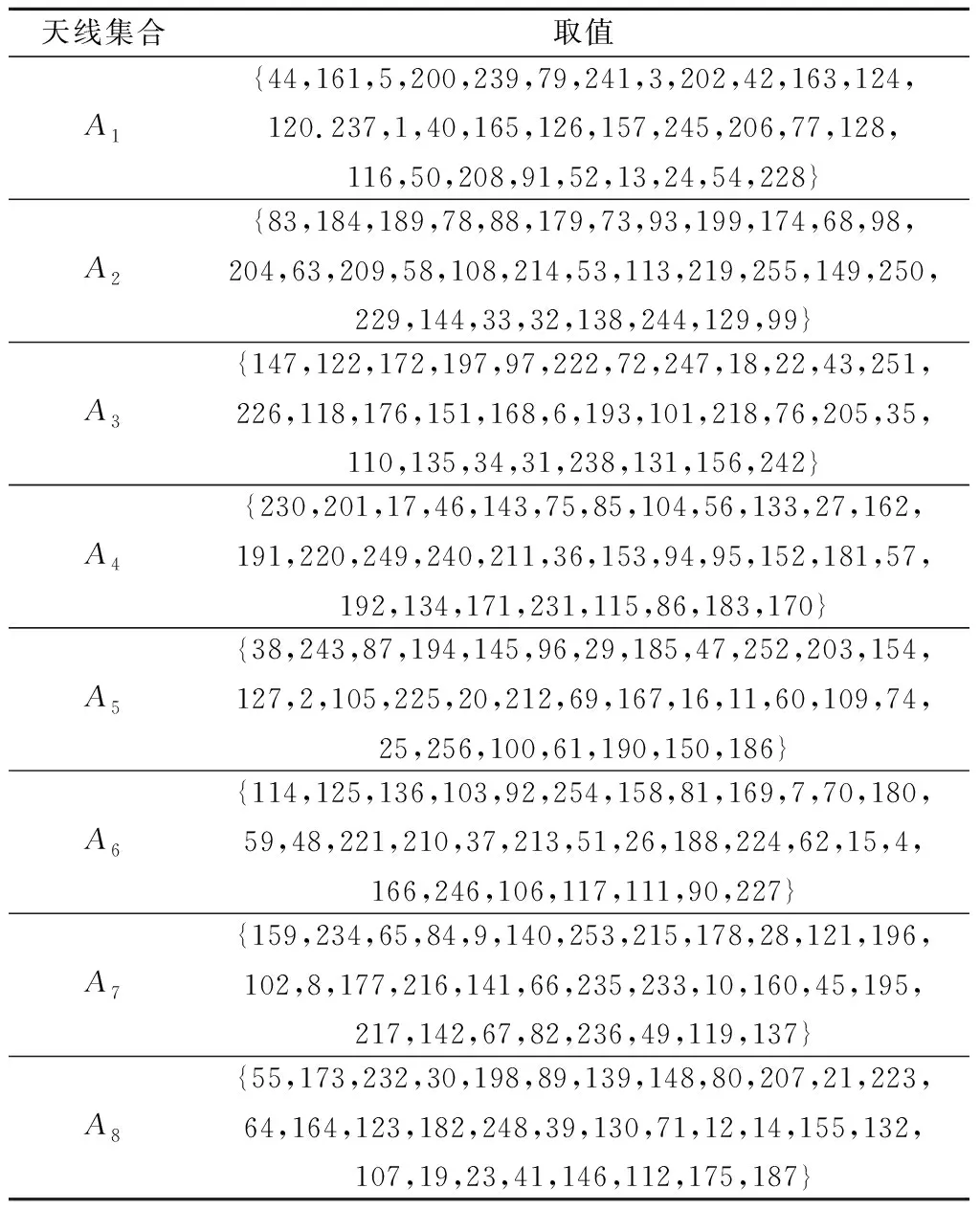
由上述预编码设计步骤,基于DSC-HA的预编码设计方案的计算复杂度主要集中在步骤1、步骤5和步骤12。在步骤1中,需采用KM算法遍历所有顶点来实现天线分组,最坏情况下每次需要修改O(N)次顶标,对应的计算复杂度为O(N2),因此,天线分组所需计算复杂度约为O(N3)。步骤5中,实现模拟预编码设计,其所需计算复杂度约为O(N2B)。步骤12中,确定数字预编码涉及矩阵乘法和矩阵求逆运算,其计算复杂度约为O(M3)。因此,基于DSC-HA的预编码设计方案的复杂度约为O(N3+N2B+M3)。基于FC-HA的预编码方案和基于SC-HA的预编码方案[14]的复杂度分别约为O(MN2B+M3)和O(N2B+M3)。而通常M≪N。因此,这3种方案计算复杂度满足关系:O(N2B+M3) 本节通过数值仿真对基于DSC-HA预编码方案(以DSC-HA-NOMA表示)进行评估,并与FD-A、基于FC-HA的mMIMO-NOMA和mMIMO-OMA(分别以FC-HA-NOMA和FC-HA-OMA表示)系统和基于SC-HA的mMIMO-NOMA、mMIMO-OMA(分别以SC-HA-NOMA和SC-HA-OMA表示)等方案[14]相比较。仿真参数设置如表2所示。 表2 仿真参数 在K=30,N=256,B=4 bits时,图2给出了不同预编码方案在不同信噪比(signal to noise ratio,SNR)下系统和速率的变化曲线。从图2中可看出,FD-A方案的系统和速率最高,但其硬件成本非常高;SC-HA方案虽然降低了系统功耗,但由于特殊的硬件结构,很大程度上限制了波束赋形增益,因而其系统和速率最低;FC-HA-NOMA方案的和速率性能十分接近FD-A方案,但其能效明显低于DSC-HA-NOMA方案。在整个SNR范围内,所提DSC-HA方案性能均优于SC-HA-NOMA和SC-HA-OMA方案;随着SNR增加,受NOMA技术优势的影响,使得本文提出的DSC-HA-NOMA的性能甚至优于FC-HA-OMA,从而验证了本文所提方案在多用户mMIMO-NOMA系统中具有优良的性能。 图2 系统和速率随SNR变化曲线Fig.2 System sum rate versus SNR 与图2仿真配置条件相同,图3给出了不同预编码方案的系统能效随SNR变化曲线图,其中系统能效定义为 (23) 式中:PRF为每个RF链所需功率;PAPS为每个APS的功耗;PBB为基带功耗;NAPS表示APS的个数。对于FC-HA方案,所需APS数为MN;对于SC-HA和DSC-HA方案,APS数为N。能效计算式(23)中各单元的功耗具体值见文献[21]。 图3 系统能效随SNR变化曲线Fig.3 System energy efficiency versus SNR 由图3发现,所提DSC-HA-NOMA方案的能效明显优于现有对比方案。FD-A方案由于RF链数等于BS发射天线数而导致系统能效最低;FC-HA方案需要8个RF链,(8×256)个APS和256个RF加法器。而SC-HA方案和本文所提DSC-HA方案仅需256个APS,且不需要RF加法器。从图4可知,随APS分辨率增加,所有方案除FD-A外,其和速率性能均逐渐提升,而且当分辨率为4 bits时,各方案和速率性能基本达到收敛,故本文仿真设置最佳分辨率为B=4 bits;且文中所提方案性能始终优于对应的SC-HA方案。 另外,由于FD-A不涉及模拟预编码设计,因此其性能不受APS分辨率影响。所以,在整个SNR范围内,FC-HA方案的能效性能明显低于SC-HA方案和本文方案。此外,无论是FC-HA还是SC-HA,采用NOMA的系统能效总是优于采用OMA的系统能效。同时,受NOMA技术潜在优势和FC-HA功耗的限制,随着SNR增加,DSC-HA-NOMA方案与FC-HA-NOMA以及FC-HA-OMA方案之间的能效差距越明显。 在N=256,K=30,SNR=10 dB时,图4给出了上述几种方案的系统和速率随APS量化比特数变化的仿真结果。 图4 系统和速率随APS量化比特变化曲线Fig.4 System sum rate versus APS quantization bit 此外,图5给出了当K=30,M=8,SNR=10 dB,B=4 bits时,不同预编码方案的系统和速率随BS天线数变化的关系曲线。 图5 系统和速率随BS天线数变化曲线Fig.5 System sum rate versus antenna number 从图5中可看出,随BS天线数增加,所有方案的系统和速率均明显提升,表明BS天线数对系统和速率性能影响非常明显。同时,与对应的OMA系统相比,无论采取何种预编码结构,NOMA系统均具有明显的优势。此外,在系统功耗几乎相同的情况下,本文所提DSC-HA-NOMA方案的性能要明显优于SC-HA-NOMA方案。 由于文中采用KM算法来实现动态天线分组,因此在N=256,M=8条件下,表3给出DSC-HA-NOMA方案一次信道实现时,与各RF链对应的天线动态分组情况。其中,Am表示与第m(m=1,2,…,M)个RF链相连的BS端天线集合。DSC-HA方案中各RF链与发射天线间的连接更为灵活,从而打破了SC-HA中模拟预编码矩阵的对角约束条件,使各RF链能够与其BS发射天线实现优化匹配。因此,DSC-HA方案的系统和速率和能效明显优于SC-HA方案。 表3 DSC-HA方案中与各RF链对应的天线分组情况 为了发挥毫米波mMIMO-NOMA系统的优势,同时有效地降低系统功耗和用户间干扰,本文基于DSC-HA提出一种高效预编码方案。在该方案中,首先在用户分成若干NOMA簇的基础上,基于等效信道增益最大化原则利用KM算法联合设计DSC网络,进而实现模拟预编码设计。接着,为了消除各NOMA簇间干扰,基于ZF准则设计数字预编码器。最后,为了减小簇内用户间干扰,以系统和速率最大化为目标,对簇内强弱用户的功率进行优化。仿真结果表明,DSC-HA方案的系统和速率明显优于SC-HA方案,且能效显著优于FD-A和FC-HA方案。此外,尽管本文所提方案假设BS采用均匀线阵,实际上相关结果可直接扩展到均匀面阵情形。4 仿真分析
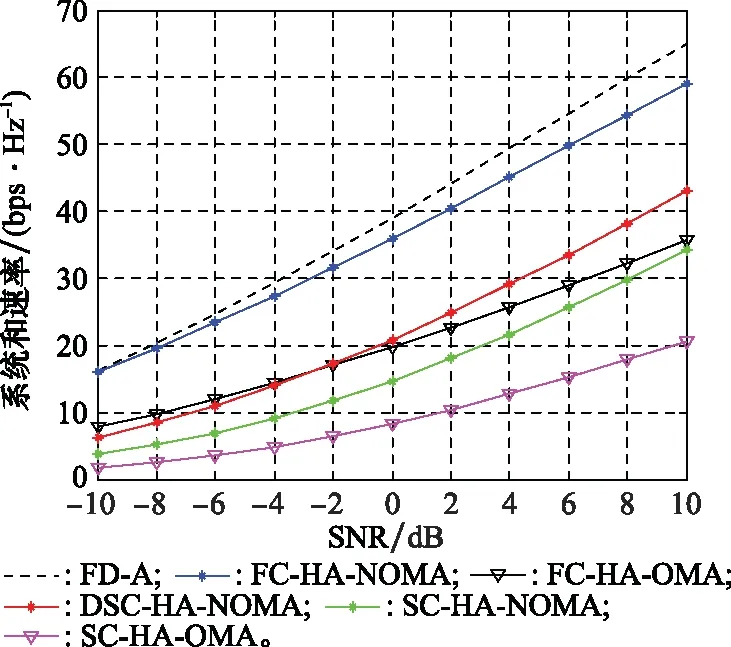
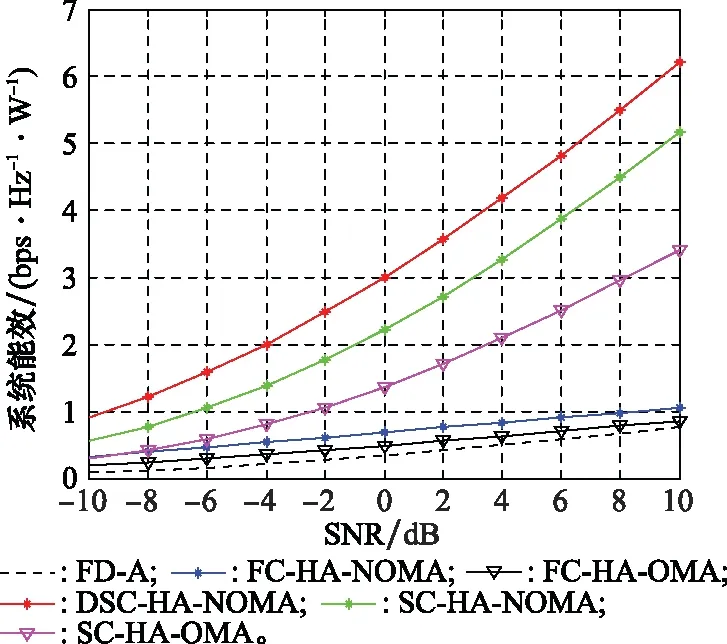
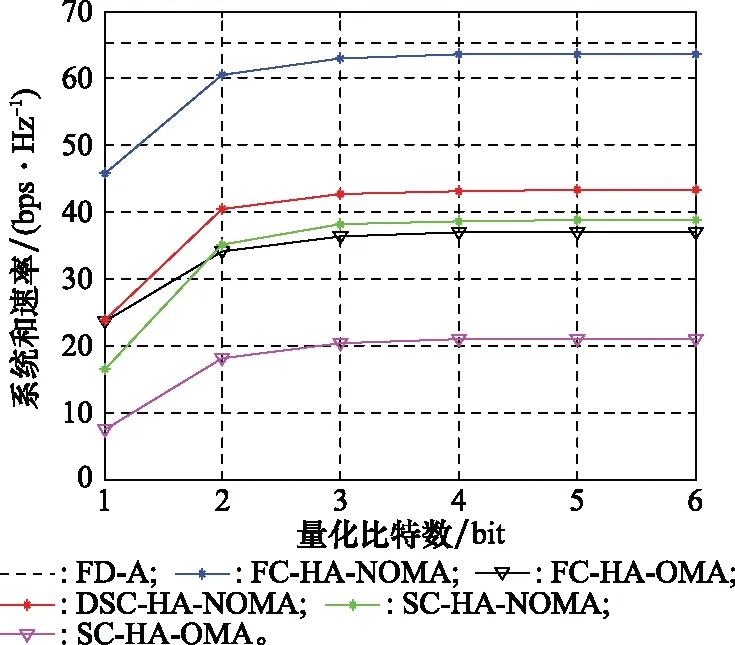
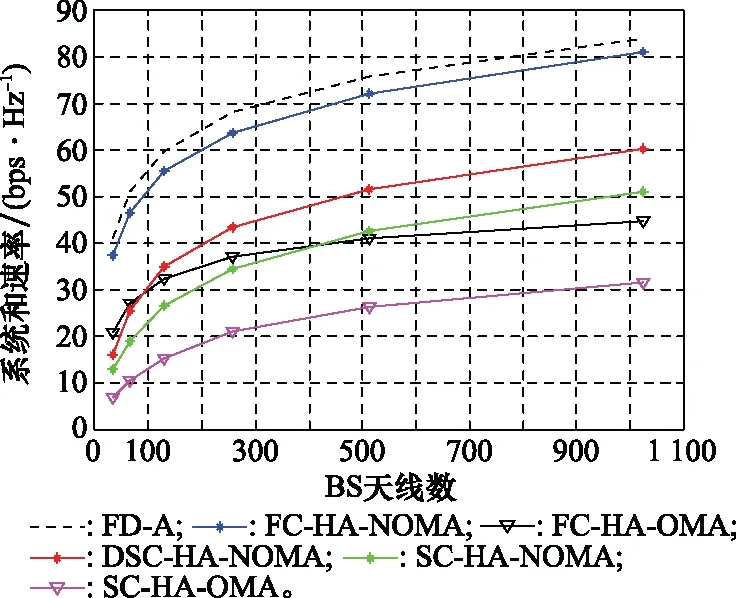
5 结 论
