李文刚1,2, 汪流江1,2,*, 方德翔1,2, 李玉玮1,2, 黄 郡3

(1. 西安电子科技大学通信工程学院, 陕西 西安 710071; 2. 西安电子科技大学综合业务网理论及

关键技术国家重点实验室, 陕西 西安 710071; 3. 国防科技大学电子对抗学院, 安徽 合肥 230037)

0 引 言

近些年来,无人系统受到了比较广泛的关注,并在无人车、无人飞行器、无人潜水器、无人船等领域取得了长足的发展[1]。水面无人艇(unmanned surface vessel, USV)是一种新型的智能无人水面平台,能够在复杂的水域环境中完成复杂的工程科研任务[2]。

USV所行驶的环境比较复杂,容易受到障碍物的影响,因此USV需要很高的自主性系统,路径规划是其中最为重要的系统之一[3]。USV的路径规划系统可以分为两种,一种是针对静态障碍物进行躲避的全局路径规划系统[4];另一种是实现USV对动态障碍物进行躲避的局部路径规划系统。

国内外学者对于路径规划系统已经研究出了很多相关的算法。巩敦卫[5]等人为了解决多地貌环境下的移动机器人路径规划问题,提出了多目标微粒群优化算法,但此算法不能完全适用于复杂的海洋环境。Kozynchenko[6]等人把人工智能(artificial intelligence, AI)算法与USV的路径规划问题进行有机结合,解决了局部路径规划问题。巩敦卫[7]等人针对密集障碍物环境下存在控制偏差的机器人路径规划问题,提出了一种基于凸包和微粒群路径规划算法,但此算法不适用于存在动态障碍物的情形。Zhang[8]等人提出一种改进的多目标粒子群算法,解决了具有不确定危险源的机器人路径规划问题,但其对于动态环境没有进行相对应的解决方案。YU[9]等人提出了一种A*算法与人工势场法相结合的路径规划算法,解决了路径规划问题中常出现的陷入局部极小点以至于无法找到最佳点的问题。Geng[10]等人针对搜救领域的任务分配问题,提出了一种基于粒子群算法的改进集中式算法,该算法为路径规划算法提供了一个新的思路。Wang[11]等人提出了一种多功能的路径规划器以解决复杂环境下航行的USV问题。

相对于国内的学者来说,国外学者对于USV路径规划问题进行了比较多的研究,比如将神经网络以及强化学习与路径规划问题有机结合起来进行研究[12-16]。

1 环境模型

环境模型的建立对于路径规划系统而言是非常重要的。首先需要对环境信息进行捕获,包括静态信息和动态信息[17]。然后对得到的环境信息进行环境模型的建立,所建立的模型可以完全代表USV在行驶过程中的真实环境。因此环境建模是非常重要的,其结果的好坏会影响到路径规划时搜索路径的长度以及搜索时间。本文综合考虑了实验场景的方式以及环境建模方法的便利性,考虑使用栅格法进行实验环境进行建模,对于其环境建模细节部分在下面进行了分析说明。

1.1 栅格法建模

栅格法是将整个环境划分成多个连续但不重合的网格,每个网格的状态对应所处的环境信息。通过一定的数学建模方法,将复杂且连续的USV复杂路径规划问题简化为离散的相邻栅格之间的移动问题,具体的操作过程如下所示:

(1) 根据场景大小选择合适的粒度,将场景环境划为相同的栅格;

(2) 通过场景环境与栅格对应的位置进行一一绑定;

(3) 根据场景环境中的障碍物设置栅格地图的每个状态。

如图1所示,场景环境空间按照栅格的粒度大小进行划分,将实际环境中的障碍物区域在栅格地图中用黑色区域表示,而白色部分表示没有障碍物的区域即为可以通行的区域。S和G分别表示初始点和目标点。在对路径进行搜索时,需要对栅格位置进行标记,标记的方式主要有两种,一种为坐标法,另一种为序列法。

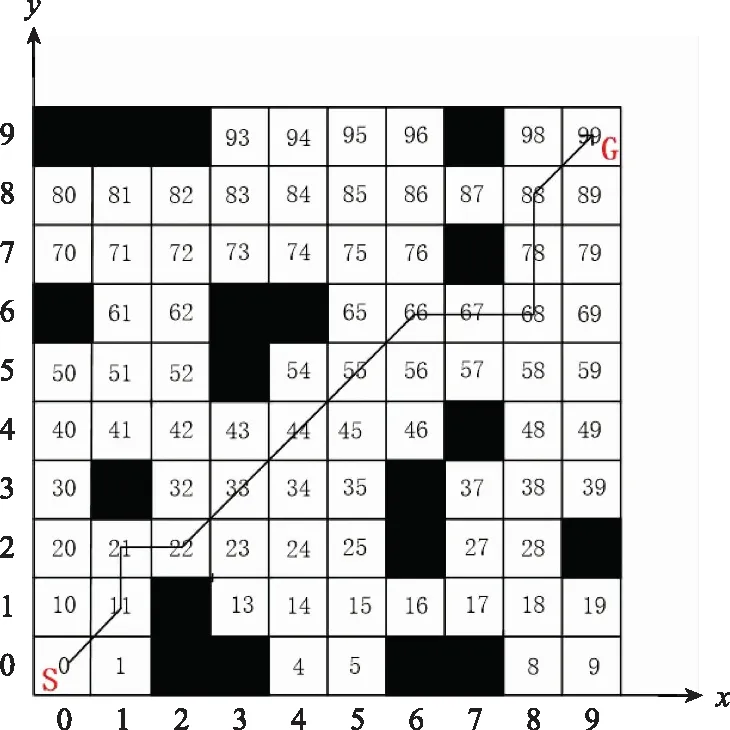
图1 栅格法示意图Fig.1 Schematic diagram of grid method

(1) 坐标法:以栅格地图的两条互相垂直的边作为平面直角坐标系的X轴和Y轴,栅格地图中的任意位置都可以用坐标(x,y)来表示。

(2) 序列法:每个网格按照一定的水平和垂直规则递增标记,每个网格都有相应的编号。

对上述两种方法进行转换的公式如下:

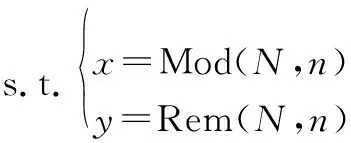
(1)

式中:x,y是利用坐标法得到的栅格地图的坐标;N表示利用序列法得到的栅格编号;n是栅格粒度因子;Mod是求余函数;Rem表示向下取整函数。

以图1为例,n=10,得到的可行路线已经在图中进行标记,利用上述两种方法对得到的可行路径可分别表示为

M1=[(0,0),(1,1),(1,2),(2,2),(3,3),(4,4),
(5,5),(6,6),(7,6),(8,6),(8,7),(8,8),(9,9)]
M2=[0,11,21,22,33,44,55,66,67,68,78,88,99]

由于上述两种不同表示方法的表示形式,本文在设计路径规划算法时,为了表示方便,采用坐标法来表示USV的运动环境。

栅格法能够降低对复杂环境进行抽象处理的复杂度,而且其算法原理以及实现过程都比较简单。但是其在进行栅格划分的时候比较复杂,需要考虑很多因素以寻求得到一个平衡。

1.2 栅格粒度确定

栅格法建模过程中最重要的一步是需要确定栅格地图的栅格粒度,其划分粒度不同,最后通过所建立的栅格地图的精度也会不同。不同的栅格粒度大小可以根据环境建立不同的栅格地图模型以及利用所建立的栅格地图进行路径搜索时所需要的时间也更不相同,甚至所得出的路径也不尽相同。

栅格粒度大小是由该区域的障碍物在整个仿真环境所占的比重来确定的,当障碍物所占的比重小时可能会产生不良影响,以至于得到一个不准确的搜索结果。反之可以增大所确定的栅格力度大小,在得到一个比较好的路径搜索结果时,降低算法进行搜索时所用的时间[18]。根据上述所提到的栅格粒度处理原则,考虑使用如图2所示的60×60的栅格地图进行仿真,分析所提出算法的优势。

图2 栅格粒度Fig.2 Grid granularity

2 A*算法的改进

2.1 A*算法概述

A*算法综合了Dijkstra算法和宽度优先搜索算法的优点,提出了一个类似于宽度优先搜索算法中的启发式函数来对路径进行评价,并将其用来评估初始节点到当前节点所消耗的代价以及当前节点到目标终点预计需要消耗的代价。评价函数的输出用于评价当前节点的某个邻域内的所有节点的输入,其评价函数可以表示为

f(n)=g(n)+h(n)

(2)

式中:g(n)表示从初始节点到当前节点n已经产生的消耗代价;h(n)表示从当前节点到目标终点预计还需要的消耗代价;f(n)表示综合两种不同代价的全局代价值。

式(2)中的g(n)与h(n)存在互相制约的关系,其中h(n)可以认为是启发函数,是影响A*算法的时空复杂度最为重要的因素之一[19]。A*算法在实际路径搜索过程中的流程如图3所示。

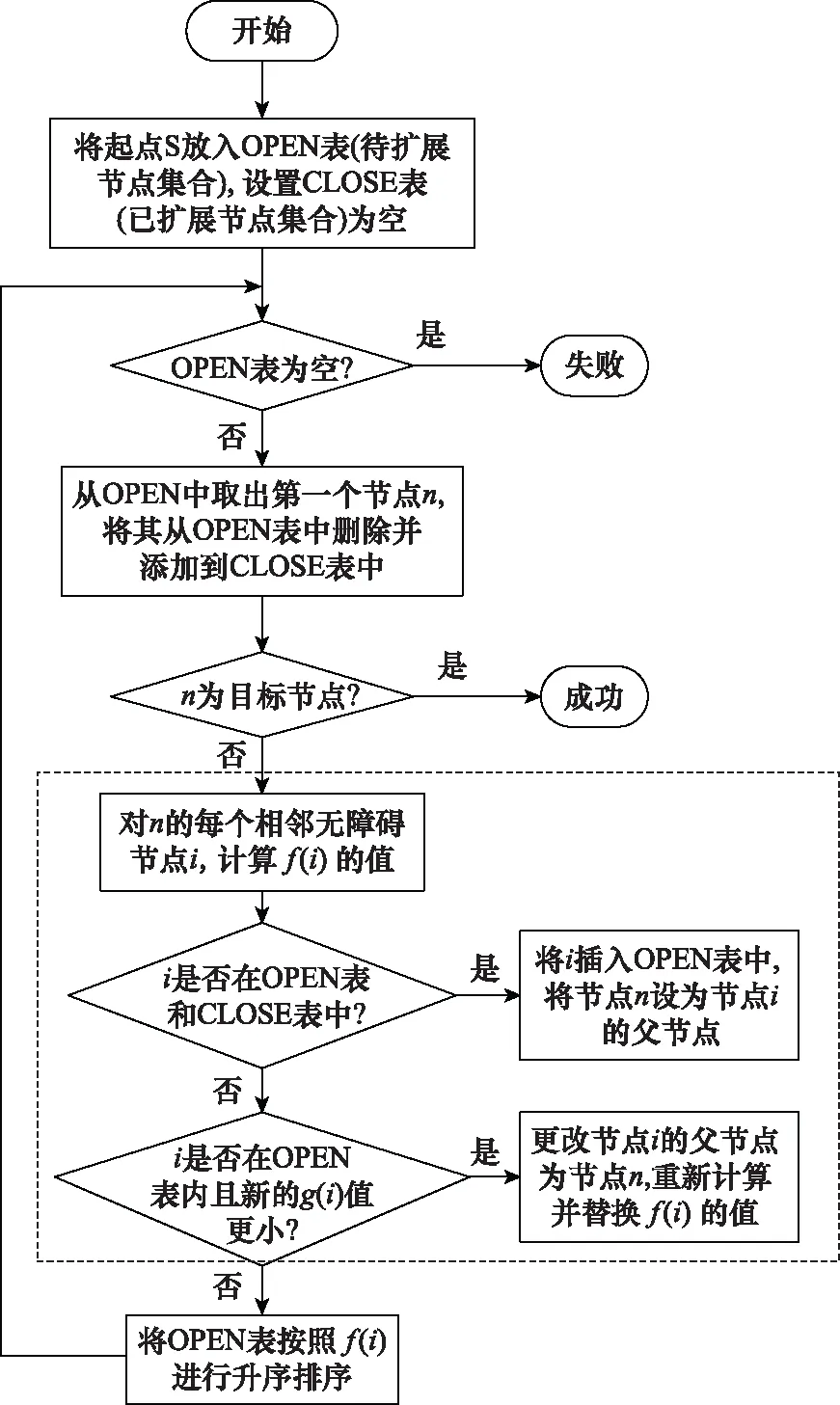
图3 A*算法流程图Fig.3 A* algorithm flow chart

2.2 堆结构优化OPEN列表

当USV在广阔的海洋环境行驶采用A*算法时,会使得需要存储的节点个数成指数级别增长。考虑到往OPENLIST中添加节点时,不会考虑到所添加节点的大小,当需要得到数值最小的节点时,需要遍历一遍存储数值的容器,当节点数量比较多时,需要耗费的时间比较长。因此为了降低节点增添所带来的时间复杂度,考虑使用堆结构来构建OPENLIST列表,堆的根节点即为列表的最小值,增删查改的时间复杂度可以大大降低,结构示意图如图4所示。

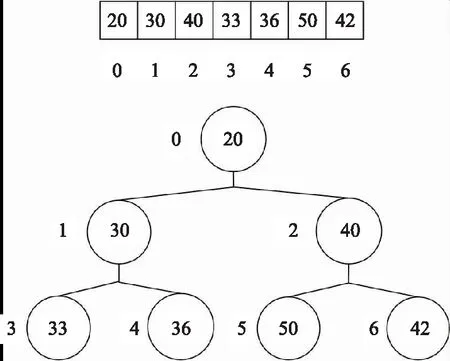
图4 堆结构的存储Fig.4 Storage of heap structures

当利用改进的堆结构OPENLIST添加数据时,所进行的操作如下:

步骤 1将所要添加的新节点插入到堆结构的尾部;

步骤 2通过比较新节点与其插入位置的父节点大小进行比较,如果所插入的节点值小于父节点值,则满足交换操作,需要交换两个节点之间的位置;

步骤 3重复进行步骤2的操作,直到不满足交换条件时停止操作。

当向堆结构优化的列表中修改和删除数据时,操作方法与插入数据类似,不再一一赘述。

2.3 双向A*算法

由于海洋环境比较宽阔,导致所选取的目标点与起始点的距离比较远,所建立的栅格地图中栅格的数量也比较多。因此单向A*算法寻找路径所需要的时间会变得很长，并且存储节点所需要的空间变得很大。为了A*算法在大规模栅格数量搜索时出现的问题,本文对传统的A*算法进行一定的改进,同时在目标点和起始点进行路径搜索。

本文所提出的双向A*算法的详细步骤如下。

步骤 1建立两个不同的OPEN列表,一个用于存储由目标点向起始点方向搜索过程中还没有检查过的点,而另一个存储由起始点向目标点方向搜索过程中还没有检查过的点。同时，两个不同的CLOSE列表并置为空列表,一个用于存储由目标点向起始点方向搜索过程中已经遍历过的点,一个用于存储由起始点向目标点方向搜索过程中已经遍历过的点;

步骤 2将初始节点S添加到存储由起始点向目标点方向搜索过程中还没有检查过的点的OPEN列表中,将目的节点G添加到存储由目标点向起始点方向搜索过程中还没有检查过的点的OPEN列表中;

步骤 3同时由目标点和起始点向各自的方向进行搜索,搜索方法与A*搜索一致;

步骤 4当某个OPEN列表的节点在另一个CLOSE列表当中时,此时已经得到了最终路径,搜索完成,返回搜索结果。

2.4 算法仿真

对上述两种算法在USV路径规划中进行相应的分析,在Matlab 2019a中进行了相关仿真,以对比双向A*和传统的A*算法的搜索效率,仿真场景是由真实的航行环境经过上述所提到的建模方法得到的60×60的栅格地图。在本节的仿真实验中,分别对两种算法进行同一个起始点和相同的目标点路径规划,并对两种算法的路径规划结果的长度以及路径的搜索时间进行对比,仿真结果及分析如下所示。

图5是A*算法的仿真结果,仿真所设置的起点的坐标是(34,54),终点的坐标是(27,16)。其中,图5(a)中的阴影部分表示的是A*算法在进行路径搜索过程中的扩展过程,图5(b)中的红色路径表示的是A*算法最后路径搜索结束后的路径规划结果,图5(b)蓝色圆圈代表的是本次A*算法仿真所设置的起始点坐标,图5(b)的蓝色五角星代表的是本次A*算法仿真所设置的目标点坐标。从本次的仿真结果可以看出,通过A*算法可以完成USV的全局路径规划,以实现从起始点到终点的避障规划。图6是双向A*算法的仿真结果,仿真所设置的起点的坐标是(34,54),终点的坐标是(27,16)。其中,图6(a)中的阴影部分表示的是双向A*算法在进行路径搜索过程中的扩展过程,图6(b)中的红色路径表示的是双向A*算法最后路径搜索结束后的路径规划结果,图6(b)蓝色圆圈代表的是本次双向A*算法仿真所设置的起始点坐标,图6(b)的蓝色五角星代表的是本次双向A*算法仿真所设置的目标点坐标。从本次的仿真结果可以看出,通过双向A*算法可以完成USV的全局路径规划,以实现从起始点到终点的避障规划。

图5 A*算法仿真图Fig.5 A* algorithm simulation diagram

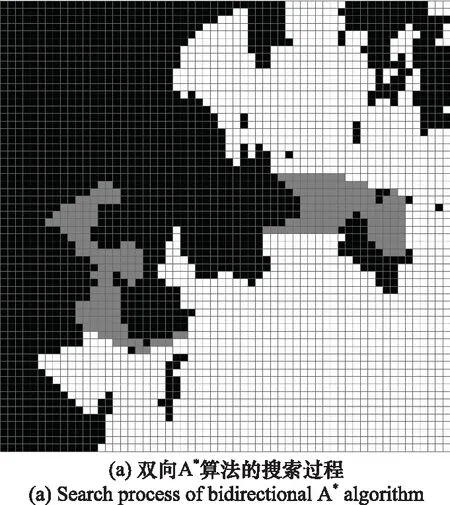
在上述仿真环境中,USV起始点的坐标为(34,54),USV的终点坐标为(27,16),对本次仿真两个算法的仿真结果从长度、时间与节点数量3个评价指标进行比较,结果如表1所示。

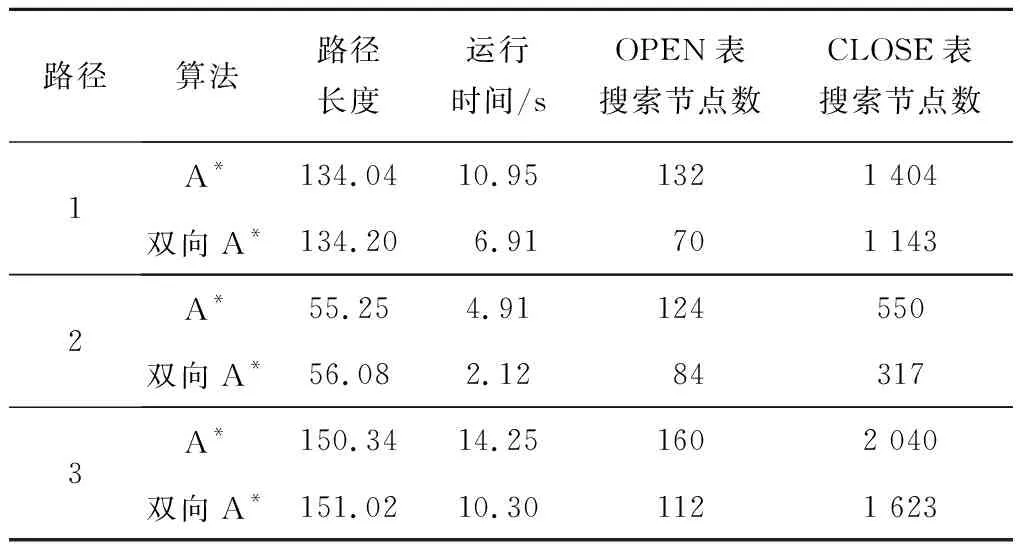
表1 A*算法与双向A*算法仿真结果对比

由表1的仿真结果进行数据分析可以发现,双向A*算法在运行时间以及搜索的节点数量上与A*算法进行比较,发现前者的算法运行时间大致上缩短了40%,算法执行过程中所产生的变量占用的内存减少了36%。从本节的仿真结果可以看出,所提出的双向A*算法与A*算法相比,在保证正确的搜索路径上,还能节省程序所执行的时间以及程序执行过程中所生成的变量需要的空间,因此可以考虑用双向A*算法代替经典的A*算法完成USV的路径规划,以得到一条安全且无差错的从起始点到终点的路径。

3 动态窗口法

在比较宽阔及复杂的海域上想要进行无差错的行驶,需要对地图中已经标记的障碍物进行规划躲避,还需要实时监测所行驶的环境,实现动态障碍物的躲避,而局部路径规划刚好可以处理这个比较棘手的问题,因此USV的局部路径规划是值得去探索深究的一个方向。本文使用DWA来完成上述所提到的问题,能够得到比较正确的USV局部路径规划结果,结合上文提到的改进的A*算法中的评价函数,考虑到海况的级别对评价函数进行相应的改进,确定相应的权重系数,以应对USV在海洋环境行驶时出现的一系列突发情况。

图7为DWA示意图,USV用黑色的船来表示,障碍物用灰色矩形来表示,图中的曲线代表USV的航行轨迹。

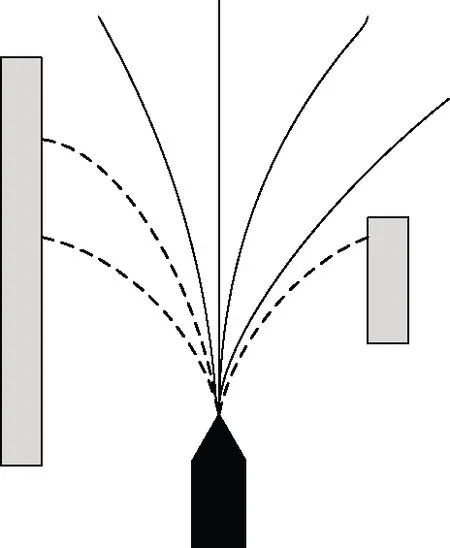
图7 DWA示意图Fig.7 Schematic diagram of DWA

如图7所示,虚线代表预测到的轨迹会与障碍物发生碰撞,因此在进行路径规划的时候会直接排除掉这些不安全的规划结果,然后,在那些实线的轨迹即不会碰到障碍物的安全轨迹中根据每条轨迹的评价函数得到最终的路径规划结果。

3.1 运动模型

DWA的主要思路是根据预测轨迹来确定下一时刻的行进方向及行进速度,因此确定行进轨迹的模型就非常重要,本节所设计的模型主要是为了确定位置与速度、时间间隔等之间的关系。

在本节中可以考虑USV的线速度vt与角速度ωt是不受对方干扰的,也就是说这二者是相互独立的,而USV的行进方向也主要由这两者确定,因此可以考虑用速度对(vt,ωt)来确定行进的轨迹。在本文中,仅考虑USV在单位时间间隔内处于匀速运动的情况,因此可以根据速度的改变判断行进方向的改变。

USV的行进方向可以是向前也可以以任意角度进行转向,假设USV在单位时间Δt内的速度可以用(vt,ωt)来表示,USV的位置坐标用(x0,y0)来表示,USV的方向角用θt来表示, USV的位置以及方向角的更新方程为

(3)

3.2 轨迹评价函数

本文在传统的DWA评价函数中考虑了外部因素的影响,增加了外部因素对评价轨迹的影响权重,其定义如下:

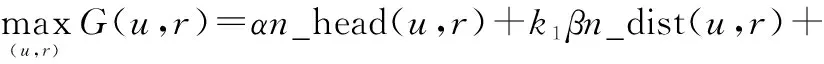
(4)

由式(4)可以看出,最终评价值是由n_head(u,r)、n_dist(u,r)和n_vel(u,r)这3个评价函数得到的[20]。式(4)中的α,β,γ分别是n_head(u,r)、n_dist(u,r)和n_vel(u,r)的初始化的权重值,k1,k2分别表示海面状况系数的权重系数,定义如下:

(5)

式中:F表示不同的海况环境的级别,(ρ,η)∈(0,1)。由式(5)可以看出,当目前的环境不适合航行时,k1会相应地进行增加,k2同时也会不断减少,这样能够得到比较正确的路径规划[20]。

为了让得到的路径转折点数量更小,需要对前文中所提到的评价函数进行归一化操作,具体流程如下所示:

(6)

(7)

(8)

式中:head(i)是航向角;dist (i)表示当前位置距离障碍物之间的距离;v(i)表示USV此时的行驶速度。

3.3 DWA算法仿真

对上述所提到的DWA算法在USV路径规划中进行可行性分析,在Matlab 2019a中进行了相关仿真,以验证DWA算法在拥有动态障碍物和静态障碍物两种不同场景下的性能,仿真场景是由真实的航行环境经过所提建模方法得到的栅格地图。在本节的仿真实验中,分别对DWA算法设置动态障碍物和静态障碍物两种场景进行仿真分析,仿真结果如下所示。

图8是DWA算法对静态障碍物避障的仿真结果,其中仿真所设置的起点坐标是(49,34),终点坐标是(17,51)。其中,图8(a)蓝色圆圈代表的是本次DWA算法仿真所设置的起始点坐标,红色五角星代表的是本次DWA算法仿真所设置的目标点坐标,绿色部分表示的是DWA算法中所涉及到的滑动窗口。图8(b)中的蓝色路径表示的是DWA算法最后路径搜索结束后的路径规划结果。从本次的仿真结果可以看出,通过DWA 算法可以完成USV的路径规划,以实现从起始点到终点的避障规划。

图8 DWA未受到动态障碍物影响仿真图Fig.8 Simulation diagram of DWA not affected by dynamic obstacle

图9的仿真场景所设置的仿真环境包含了动态障碍物,这与图8中的静态障碍物的仿真场景不同,但其余的条件与图8的仿真场景基本相同。图9是DWA算法对动态障碍物避障的仿真结果,仿真所设置的起点的坐标是(59,19),终点的坐标是(38,44)。其中,图9(a)蓝色圆圈代表的是本次DWA算法仿真所设置的起始点坐标,红色五角星代表的是本次DWA算法仿真所设置的目标点坐标,绿色部分表示的是DWA算法中所涉及到的滑动窗口。图9(b)中的蓝色路径表示的是DWA算法最后路径搜索结束后的路径规划结果。从本次的仿真结果可以看出，通过DWA 算法可以完成USV对包含动态障碍物的路径规划,以实现从起始点到终点的避障规划。由上述的仿真结果可以看出,DWA算法能够躲避动静态障碍物,但是由于这种方法存在一种天然的缺陷,就是容易将局部最优值当成全局最优值进行输出,以至于USV很难到达最终目标。如图10所示,将坐标点(29,9)定为起始点,将坐标点(50,28)设置为终点时,DWA算法暴露缺陷,陷入了局部最小点,将其当成最优点导致无法得到一条正确的规划路径。为了解决上述出现的问题,本文基于DWA及改进的A*算法提出了一种全新的路径规划算法。

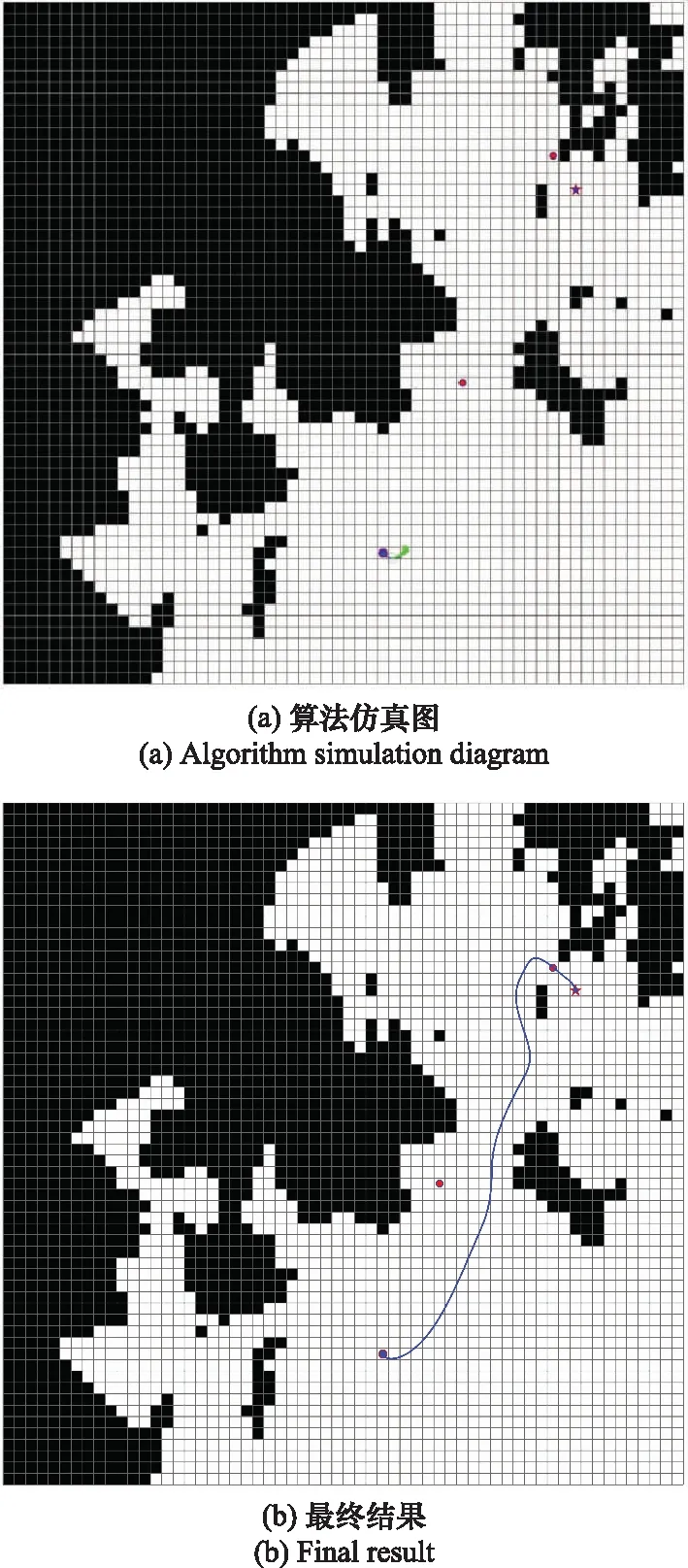
图9 DWA受到动态障碍物影响仿真图Fig.9 Simulation diagram of DWA affected by dynamic obstacle

图10 DWA陷入局部最小点Fig.10 DWA falling into local minimum

4 混合路径规划系统

4.1 混合路径规划系统建立

USV在海面航行时的真实环境错综复杂,体现在岛屿、大型水下石头等静态障碍物,还有大型海洋生物等会对USV造成影响的动态障碍物。在规划USV路径时二者均需考虑。其一, A*算法的优点是能够准确地避开静态障碍物,但是对于动态障碍物来说,此算法还无法做到能够准确无误地规划出一条完整的路径。其二,DWA算法优点是能够准确地避开动态障碍物以及其附近的一些静态障碍物,但是对于全局的静态障碍物来说,此算法还无法做到能够准确无误地规划出一条完整的路径,可能会出现第3节所提到的陷入局部最优值的问题。为了解决上述两个问题,本文提出了一种基于A*算法和DWA算法相结合的融合算法。此混合算法不仅解决了对动静态障碍物的躲避问题,还可以在保证最优路径的情况下提升路径的平滑度,使其更贴合USV的实际航行情况,具有更强的实用性。

图11为本文所提出的混合路径规划系统设计框架,主要分为全局路径规划部分以及局部路径规划部分,二者相互融合进行路径规划，其主要步骤如下。

步骤 1通过实际海洋地图经过本文的栅格处理方法得到的栅格地图来确定全局环境中的动态障碍物的分布情况,利用双向A*算法得到USV的全局路径;

步骤 2使用外部感知传感器实时感知的数据来更新局部地图,并结合步骤1中的全局路径以及得到的局部地图确定局部目标点,使用DWA算法对动态障碍物进行躲避生成局部路径规划路径,通过这种方式不断更新局部最优点使USV最终到达全局目标点,最后得到最佳的规划路径。为了获得较远的安全距离,在DWA算法中优化评价函数,加入与海面实时状况级别相关的系数。当海面航行的实时条件不断变化时,实时调整相关的系数,以使得USV能够比较安全地在海面环境上进行航行。

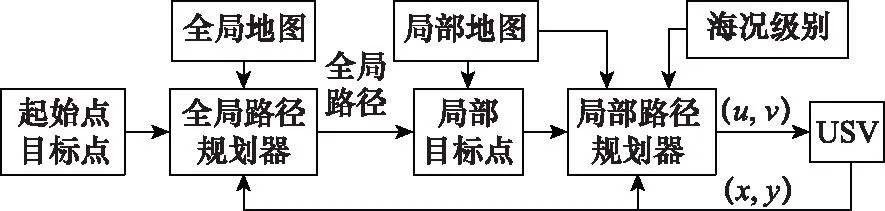
图11 混合路径规划系统Fig.11 Hybrid path planning system

对于本文所提出的USV混合路径规划系统,要做到的是充分融合A*算法以及DWA算法的优点,确保能够解决单独使用这两种算法时出现的缺点。图12展示了本文所提出的混合路径规划算法的实现步骤,不断通过局部最优点以及全局路径进行融合更新,最终得到一条安全的规划路径。

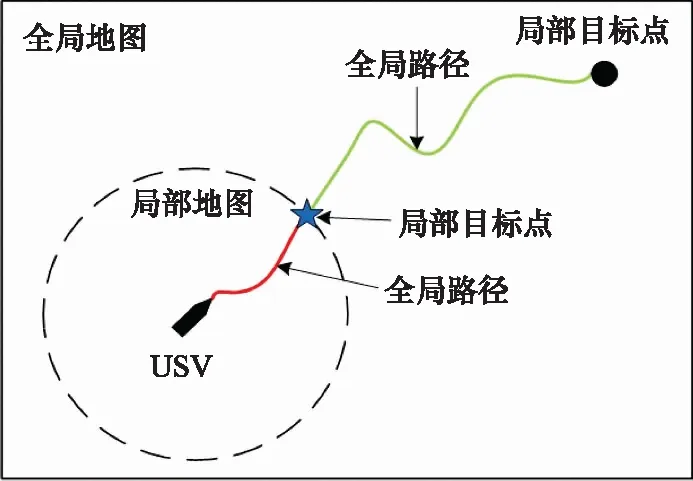
图12 局部目标点示意图Fig.12 Local target point diagram

4.2 混合路径规划算法仿真

对上述所提到的USV混合路径规划算法中进行可行性分析,在Matlab 2019a中进行了相关仿真,以验证所提算法相较于经典路径规划算法的性能,仿真场景是由真实的航行环境经过上述所提方法得到的栅格地图。如图10所示,将坐标点(29,9)定为起始点,将坐标点(50,28)设置为终点时,DWA算法暴露缺陷,陷入了局部最小点,将其当成最优点导致无法得到一条正确的规划路径。通过设置与图10相同的仿真条件来验证本文所提出的混合路径规划算法的优越性。

图13与图10的仿真将坐标点(29,9)定为起始点,将坐标点(50,28)设置为终点,通过双向A*算法得到的全局路径在图13中用红色路径表示,蓝色路径表示的是通过DWA算法同时结合全局搜索路径得到的最优路径。

图13 混合路径规划算法仿真Fig.13 Hybrid path planning algorithm simulation

表2展示了两种算法得到路径的路径长度和路径拐点,通过两组数据分析得出混合算法相较于改进的A*算法,其路径长度缩短了21%,路径拐点降低了59%。

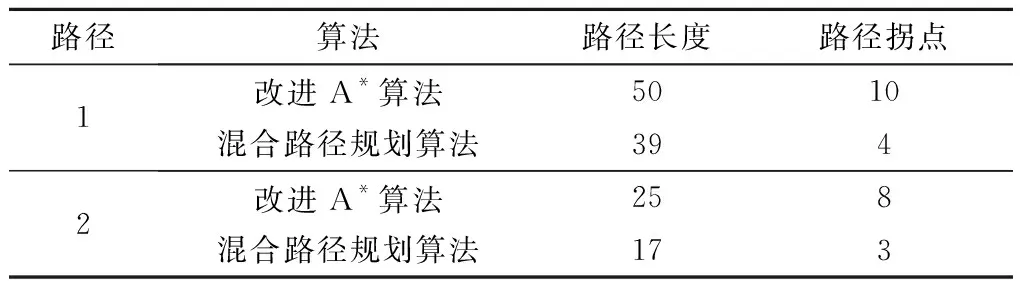
表2 混合算法与A*算法仿真结果对比

由图13和表2的结果可以看出,本文所提算法能够得到一条完整的规划路径,其结合了双向A*算法以及DWA算法的优点,同时弥补了这两种算法的缺点,得到的路径的拐点数还较少,更方便USV在海面上进行安全行驶。

5 算法时间复杂度分析

传统的A*算法在最坏的情形下,即评价函数中实际代价函数发挥主要作用,此时算法被简化为Dijkstra算法,从而计算量增加,此算法在运行过程中会遍历还没到达的节点,因此整个算法的运行时间为O(n2)[21](其中n为节点的个数),而本文所提算法的运行时间主要是由堆排序决定的,在排序过程中的时间复杂度小于或等于满二叉树的高度log2n,故整个算法运行时间的复杂度为O(nlog2n)。由于DWA遍历运行的时间复杂度是线性的,因此本文提出的混合路径规划算法的时间复杂度取决于本文提出的改进A*算法。

6 结 论

USV路径规划系统主要分为两种路径规划系统,一种为全局路径规划系统,另一种为局部路径规划系统,本文对这两种路径规划算法进行改进,提出一种基于DWA和改进A*的混合路径规划算法。本文所采用的改进A*即双向A*算法在运行时间以及算法搜索的节点数量上与传统A*算法进行比较,发现前者的算法运行时间大致上缩短了40%,算法所产生的变量所占用的内存减少了36%。基于DWA和改进A*的混合路径规划算法相较于改进的A*算法,其路径长度缩短了21%以及路径拐点降低了59%,性能得到大幅度提升。