基于改进粒子群算法的快速反射镜自抗扰控制
2021-11-29冯建鑫王雅雷
冯建鑫, 王雅雷, 王 强, 胥 彪
(南京航空航天大学航天学院, 江苏 南京 211106)
0 引 言
快速反射镜(fast steering mirror, FSM)具有转动惯量小、跟踪精度高、结构紧凑、响应速度快等优点[1-3],被广泛应用于量子定位[4]、空间激光通信[5]、图像稳定[6]、高能激光武器[7]以及其他高精度跟踪瞄准等领域。这些领域均需要FSM具有较高的跟踪精度和较强的扰动抑制能力,这就要求FSM的控制器要具有很好的控制性能,比例-积分-微分(proportion integration differentiation,PID)控制器虽然结构简单,参数整定容易,但其所能达到的控制精度和对干扰的抑制能力还有待提升。因此,有学者尝试对PID控制器进行改进,文献[8]将自适应强跟踪卡尔曼滤波器与PID控制器相结合,在考虑卫星平台抖动以及工作环境噪声的情况下,可将FSM的跟踪精度控制在±2 μrad,但文中只考虑了FSM跟踪低频正弦信号的能力。文献[9]在经典PID控制器的基础上,引入模糊设计思想和参数自整定的方法,设计了模糊自适应PID控制器,但文中只验证了FSM跟踪阶跃信号的能力。自抗扰控制器(active disturbance rejection control, ADRC)具有控制精度高、抗干扰能力强的优点[10-12],将ADRC用于FSM前期也有学者做了一些工作。其中,文献[13]面向航空光电载荷音圈电机驱动的FSM控制问题,采用了降价自抗扰控制,提升了FSM的动态性能和稳态精度,对工程设计具有较大的参考价值。文献[14]将模糊控制与自抗扰控制相结合,设计模糊ADRC,在考虑卫星平台振动的情况下,用FSM跟踪不同幅值和不同频率的信号,但FSM的跟踪精度还应进一步提高。
综上,本文中FSM用于空间激光通信中的复合轴控制系统,主要作用是消除系统中的中高频噪声,在考虑卫星平台振动的情况下仍需要具有较高的跟踪精度。综合考虑之后,本文拟采用自抗扰控制策略。针对ADRC参数整定难的问题,本文提出一种惯性权重基于箕舌线函数调整的改进粒子群优化(improved particle swarm optimization, IPSO)算法,该算法在迭代前期惯性权重大且改变率慢,后期惯性权重小且改变率快,与标准粒子群优化(particle swarm optimization, PSO)算法相比,更有可能找到所优化问题的全局最优解,随后通过5个经典的测试函数验证本文对PSO改进方式的有效性。最后将基于IPSO、PSO的ADRC和PID控制器分别用于FSM控制系统,验证了基于IPSO的ADRC与其他两种控制器相比可以更有效地抑制系统中的扰动,对不同频率的高频正弦信号也具有更好的跟踪效果。
1 FSM控制系统
本文研究的FSM具有柔性转轴,执行机构为音圈电机,忽略电气时间常数后,基于音圈电机驱动的FSM从电机电压输入到FSM转角输出的系统模型可以简化为一个典型的二阶环节[13],其开环传递函数如下所示:
(1)
因为本文将基于音圈电机驱动的FSM简化为一个二阶环节,故在用ADRC进行控制时,需要一个三阶的扩张状态观测器(extended state observer, ESO)来观测FSM的位置信号、速度信号和系统中的总扰动。那么,ADRC中待整定的关键参数就有β01,β02,β03,β1,β2共计5个。其中β01,β02,β03是三阶ESO的增益,β1,β2为ADRC中非线性状态误差反馈(nonlinear state error feedback, NLSEF)控制率的增益。
本文研究的重点是使用IPSO优化ADRC中的关键参数,并将得到的参数用于FSM控制,从而提高FSM的跟踪精度和扰动抑制能力,以使得FSM能够满足空间激光通信领域对系统跟踪精度的要求。结合研究重点,可以得到如图1所示的FSM控制系统结构图。
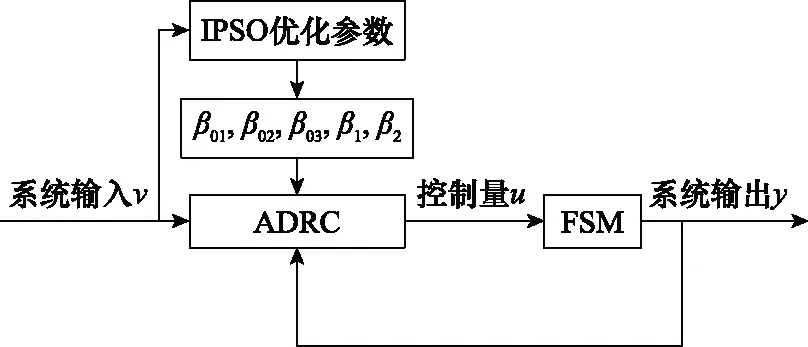
图1 FSM控制系统结构图Fig.1 Structure diagram of FSM control system
2 ADRC
ADRC由3部分组成,跟踪微分器(tracking-differen-tiator,TD)、ESO和NLSEF[15-18],组成结构图如图2所示。
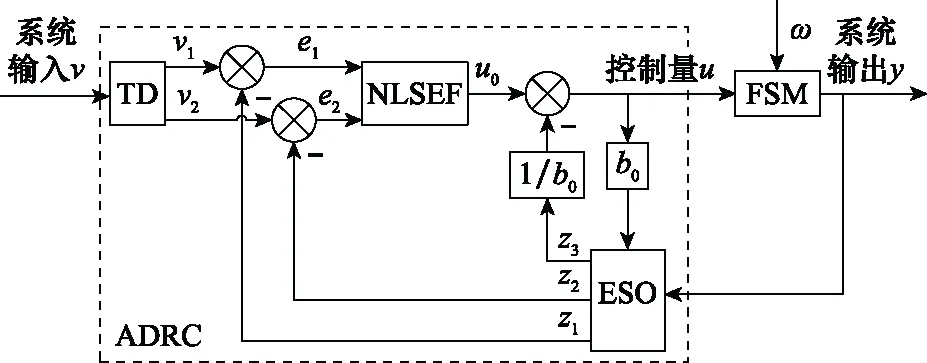
图2 ADRC结构图Fig.2 Structure diagram of ADRC
这里设定b0已知,其中ω为外界干扰。ADRC各部分对应的离散算法表示如下。
(1) TD方程
(2)
其中,fhan的表达式为
(3)
(2) ESO方程
(4)
(5)
(3) NLSEF方程
(6)
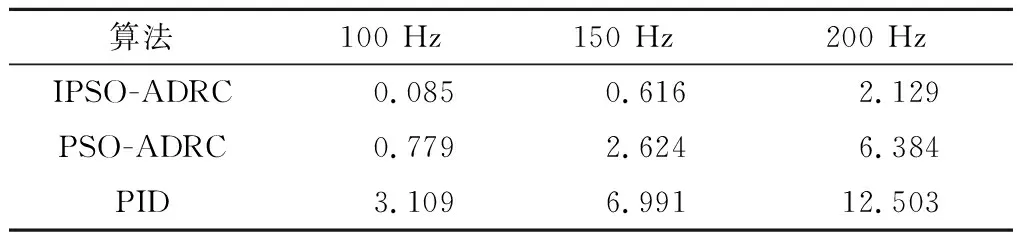
式中:0 PSO是在1995年Eberhart和Kennedy基于对鸟群觅食行为的研究,提出的一种解决最优化问题的群体智能算法[19-22]。PSO中每一个粒子的位置都代表所优化问题的一个解,粒子会根据算法优化过程中自身所到达的离食物最近的位置pbest和当前迭代次数中所有粒子距离食物最近的位置gbest计算下一刻自身的速度,从而更新自己的位置[23-24]。设某一区域内有j个粒子,则第i个粒子第k+1次迭代速度更新公式和位置更新公式如下: (7) (8) 式中:w为惯性权重,表示上一次迭代速度对当前速度的影响,传统PSO中该值一般取0.9;c1,c2为学习因子,表示当前粒子对其之前迭代过程中的最优值和当前迭代过程中所有粒子中的最优值的学习能力,通常取为2;r1,r2为0到1之间的随机数。 在传统的PSO中,惯性权重是一个常值,但惯性权重的取值在PSO搜索的不同阶段有着不同的作用,PSO在迭代刚开始时应取较大的惯性权重,以保证算法能够做到全局搜索,避免陷入局部最优,后期应取较小惯性权重,以使得算法能够更快的收敛。基于此,Shi等提出了惯性权重线性递减策略[25],虽然基于该策略设计的惯性权重,不再是一个常值,但惯性权重的变化率却是一个常值,即算法停留在全局搜索和局部开发的迭代次数一样,这样算法未必能够得到最优解。于是,南杰琼等提出一种惯性权重按正弦函数递减的策略[26],基于该策略设计的惯性权重的改变率随着迭代次数的改变在不断变化,但前期惯性权重变化速率快,后期惯性权重变化速率慢,这样有可能导致算法还没有全局搜获完毕就开始进行局部搜索,且进行局部搜索的速度慢。因此,惯性权重按正弦函数递减的策略也存在有可能使算法陷入局部最优和算法后期收敛速度慢的缺陷[27]。 针对上述缺陷,本文提出一种惯性权重基于箕舌线函数调整的IPSO。该算法在迭代前期惯性权重改变率慢,后期改变率快,更有利于算法全局搜索和局部开发的切换。其中箕舌线函数图形如图3所示。 图3 箕舌线函数Fig.3 Versoria function 图3中,OM=2a为定圆x2+y2-2ay=0的直径,将x轴绕O(0,0)点逆时针旋转θ度,分别交直线y=2a于N点,交圆于A点,过点A,N分别做x,y轴的平行线相交于点P,θ由0°逐渐增大为180°,则P点的轨迹称为箕舌线。 其中箕舌线的直角坐标方程如下: (9) 式(9)中对x求二阶导数得到: (10) (11) 式中:wmin,wmax为惯性权重最小值和最大值;ηi,ηmax为当前迭代次数和最大迭代次数,令h(i)=ηi/ηmax,并化简得 (12) 为了验证本文对标准PSO改进方式的有效性,下面将通过优化算法里面几个经典的测试函数,对改进前后PSO的性能进行测试。 为了验证本文对PSO改进方式的有效性,采用5种不同的测试函数进行测试,先后采取IPSO和PSO分别求解。另外,为了验证IPSO与其他优化算法相比的优越性,也将遗传算法(genetic algorithm,GA)[28]和蜻蜓算法(dragonfly algorithm, DA)[29]用于求解上述5种测试函数。其中上述4种算法的种群规模均为40,迭代次数均为200。由于4种算法中均有随机数,故每种算法随机测试30次,并记录30次测试过程中4种算法的平均值和最小值,若计算结果小于1×10-16,则记为0,具体的测试结果如表1所示。 表1 5种不同测试函数的测试结果 从表1中可以看出,对这5个测试函数,IPSO几乎都能够找到理论最小值,且30次测试过程中无论是平均值还是最小值均优于PSO。与GA、DA相比,在某些函数优化方面也具有一定的优越性。另外也可看出,标准PSO算法由于惯性因子是一个常值,不能够很好地平衡算法的全局搜索和局部开发的能力,测试时取0.9,虽然PSO算法可以做到全局搜索,但对数据的开发程度不够,导致30次测试过程中都没能够找到理论最小值。下面将IPSO用于优化ADRC的5个关键参数,以解决ADRC参数用人工试凑法整定效率低的问题,然后将基于IPSO的ADRC用于FSM控制,以提高FSM跟踪高频信号时的跟踪精度和扰动抑制能力。 选取系统的ITAE值作为优化算法的适应度函数,具体ITAE值表达式如下: (13) 式中:err(t)是控制系统中的误差信号,t是仿真时间。 算法流程图如图4所示。基于IPSO优化ADRC的具体步骤如下。 步骤1参数初始化。确定粒子群的规模n、惯性权重最大值wmax和最小值wmin、最大迭代次数ηmax、学习权重c1和c2的取值、最小适应度aim、粒子位置和速度的上下界。 步骤2将IPSO中粒子的位置代替ADRC中待优化的5个参数。 步骤3将步骤2得到的参数,代入模型中,进行仿真,并根据式(13)计算每个粒子的适应度。 步骤4通过最小值函数,计算粒子群的个体极值pbest和全局极值gbest。 步骤5判断gbest是否满足大于aim,若满足则运行步骤6,若不满足则跳到步骤8。 步骤6判断当前迭代次数是否满足等于ηmax,若满足则进行步骤8,否则进行步骤7。 步骤7根据式(12)更新惯性权重w,并根据式(7)和式(8)计算下一代粒子群的位置,迭代次数加1,并返回到步骤2。 步骤8算法结束,输出gbest。 图4 IPSO算法优化ADRC流程图Fig.4 ADRC flow chart of IPSO algorithm optimizarion FSM作为空间激光通信精跟踪系统中的核心部件,采用系统辨识的方法确定FSM从电压输入到位置输出的开环传递函数如下: (14) 仿真时参数设置如下:粒子群的规模为20,最大迭代次数为60,学习因子均为2,IPSO算法中惯性权重的最大值为0.9,最小值为0.4,PSO算法中惯性权重取值为0.9。本文在韩京清研究员提出的基于采样步长的幂次形式表示的经验公式的基础上,又采用试凑的方法确定粒子群落的一组初始参数,在初始参数的基础上进行适当的扩充,选取PSO与IPSO中粒子位置上下界为:ub=[22 000,3×108,1×1012,150,0.12],lb=[10 000,1×108,2×108,20,0.001],其中ADRC中除了需要优化的5个参数,其他参数取值如下:r=900 000,δ=0.1,h=h0=0.000 1,a1=0.5,a2=1.25。 本文中FSM作为空间激光通信中精跟踪的核心部件,需要与粗跟踪转台组成复合轴系统,故FSM的作用是消除粗跟踪转台的残差,以提高整个复合轴系统的跟踪精度。在工程实际中,粗跟踪转台可将跟踪误差控制±300 μrad,故对精跟踪系统而言,主要考虑其对幅值为300 μrad的高频信号的跟踪能力。另外,FSM所处的环境存在较多的外部扰动,其中对跟踪结果影响较大的是卫星平台振动。由欧洲航天局对OLYMPUS卫星进行的星体振动测试可知,对空间光通信影响较大的频率主要在100 Hz以内,另外其星体振动的功率谱密度函数为s(f)=160/(1+f2)(μrad2/Hz)[30],根据欧洲航天局给出的功率谱密度函数,设计一个滤波器以模拟卫星的平台振动,该滤波器的传递函数为 (15) 该滤波器的输入端为高斯白噪声,输出端为卫星平台振动的模拟信号,该模拟信号的功率谱密度函数不是一个常数,故该噪声为有色噪声。图5(a)为模拟的卫星平台振动信号,图5(b)为平台振动信号的幅频响应曲线。 图5 卫星平台振动模拟信号及其幅频响应Fig.5 Satellite platfrom vibration simulation signal and itsamplitude frequency response 为了测试基于IPSO的ADRC(IPSO-ADRC)、基于PSO的ADRC(PSO-ADRC)和PID控制器的控制性能(其中PID控制器参数为kp=250,ki=80,kd=0.03,该控制器参数通过试凑法取得),在考虑卫星平台振动情况下,系统中输入幅值为300 μrad,频率为100 Hz的高频正弦信号,分别用IPSO、PSO优化ADRC参数,优化后得到的5个参数和算法的最小适应度如表2所示,两种算法的适应度随算法迭代次数变化情况如图6所示。 表2 两种算法得到的5个参数和最小适应值(FSM跟踪高频正弦信号) 图6 适应值随迭代次数变化过程Fig.6 Process of fitness value changing with number of iterations 从图6中可以明显看出,在算法搜索后期IPSO与PSO相比具有更快的收敛速度,能够找到对优化问题而言更优的解。在跟踪幅值300 μrad、频率100 Hz的高频正弦信号时,IPSO-ADRC、PSO-ADRC和PID控制器控制的FSM的给定与反馈曲线图和稳态误差对比图如图7(a)和图8(a)所示。另外,为了测试控制器的对不同频率正弦信号的跟踪能力,在控制器参数保持不变的情况下,分别在系统中输入幅值300 μrad,频率为150 Hz、200 Hz的高频正弦信号,得到3种控制器控制FSM的给定与反馈曲线图和稳态误差对比图如图7(b)、图7(c)和图8(b)、图8(c)所示。图7和图8中蓝色点划线表示PSO-ADRC控制器的控制性能,绿色实线表示IPSO-ADRC控制器的控制性能,红色虚线表示普通PID控制器的控制性能。另外,图7中黑色点划线表示系统的输入信号。 图7 跟踪不同频率正弦信号时给定与反馈对比图Fig.7 Given and feedback comparison chart when tracking sinesignals of different frequencies 图8 跟踪不同频率正弦信号时稳态误差对比图Fig.8 Steady-state error comparison chart when tracking sinusoidal signals of different frequencies 从图7中可以看出,3种控制器控制的FSM到达波峰时的相位与给定输入到达波峰时的相位基本保持一致,故基于3种控制器的控制系统的稳态误差主要是由输入与输出的幅值差异所造成的,具体3种控制器跟踪100 Hz、150 Hz、200 Hz高频正弦信号稳态误差的最大值如表3所示。 表3 稳态误差最大值 从图8和表3可以看出,3种控制器的稳态误差的最大值都随着输入信号频率的增加而增大,跟踪以上3种任一频率,IPSO-ADRC的稳态误差的最大值与其他两种控制器相比都要小,在跟踪100 Hz、150 Hz正弦信号时,IPSO-ADRC可将稳态误差控制在±2 μrad以内,在跟踪200 Hz正弦信号时,IPSO-ADRC可以将稳态误差控制在±2 μrad附近,基本满足空间激光通信对系统跟踪精度的要求。 本文为了提高FSM的跟踪精度和扰动抑制能力,提出了一种基于IPSO的ADRC策略。在考虑卫星平台振动的情况下,该控制策略控制的FSM在跟踪幅值不超过300 μrad,频率不超过150 Hz的正弦信号时,跟踪精度优于2 μrad,同时需要指出的是,本设计方案未考虑测量噪声和输入噪声对系统跟踪精度的影响,这也是以后需要研究的内容。另外,基于IPSO的ADRC与基于PSO的ADRC、PID控制器相比,也具有很好的控制效果,可以明显提升系统跟踪精度和抗干扰的能力。综上,本文可以得出以下结论。 (1) 将PSO中惯性因子由常值转变为基于箕舌线函数调整,可以较好地平衡算法的全局搜索和局部开发的能力,找到对优化问题而言更优的解。 (2) 将基于IPSO的ADRC用于FSM控制,与PID控制器相比可以明显提升FSM跟踪高频信号时的跟踪精度和扰动抑制能力。3 PSO及其改进
3.1 PSO描述
3.2 IPSO
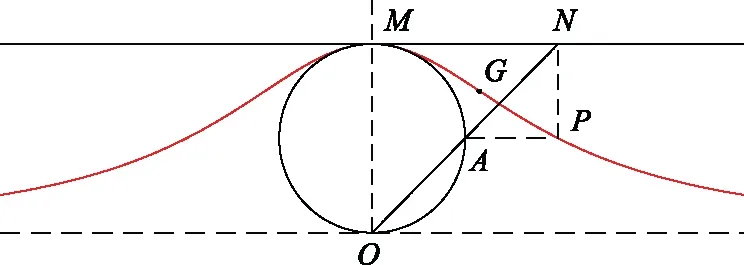
3.3 测试函数

4 基于IPSO优化ADRC
4.1 适应度函数的选取

4.2 算法流程
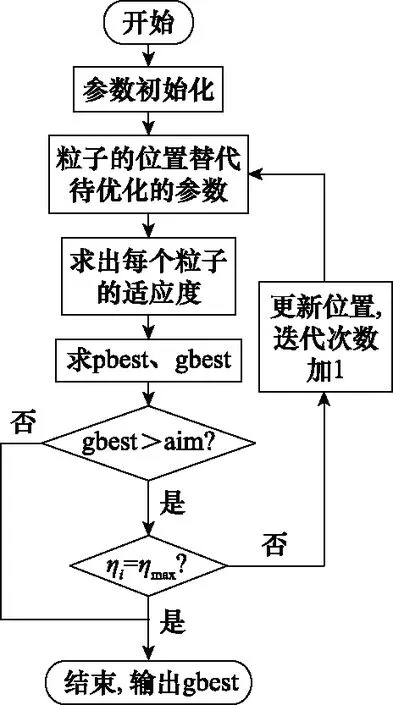
5 数值仿真
5.1 FSM模型的建立
5.2 参数设置
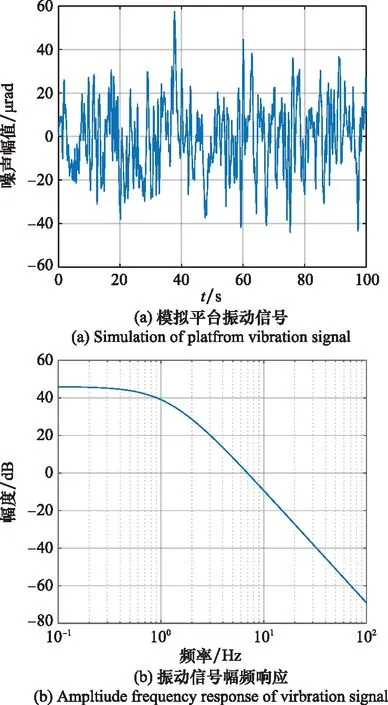
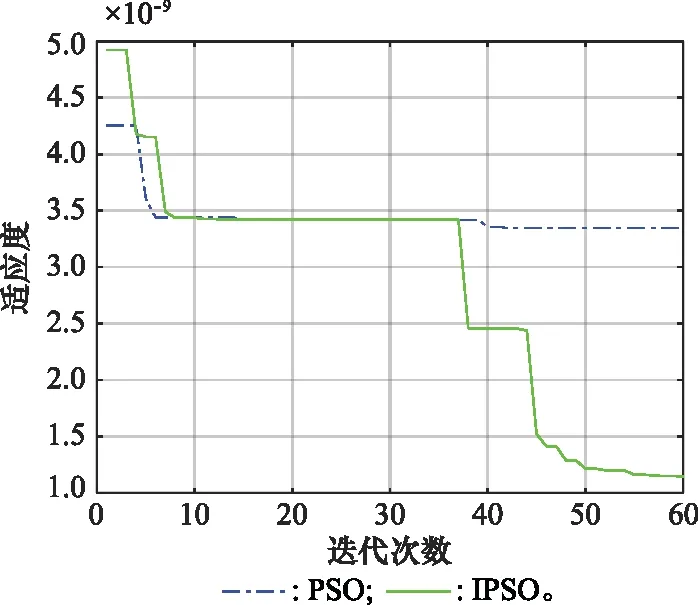
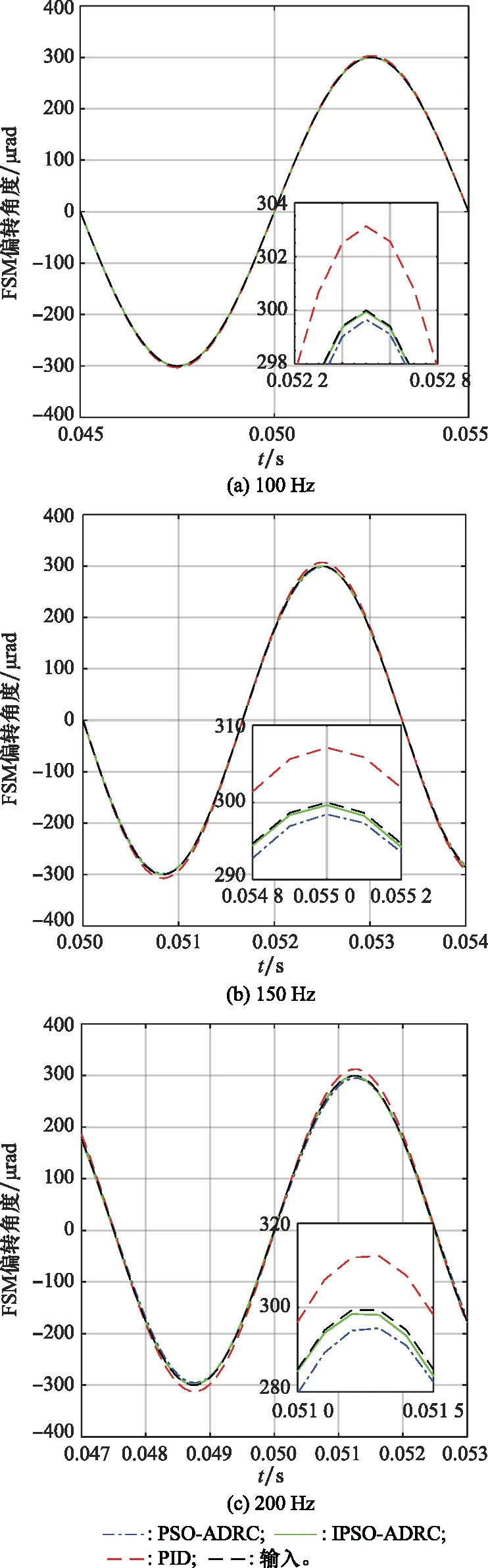
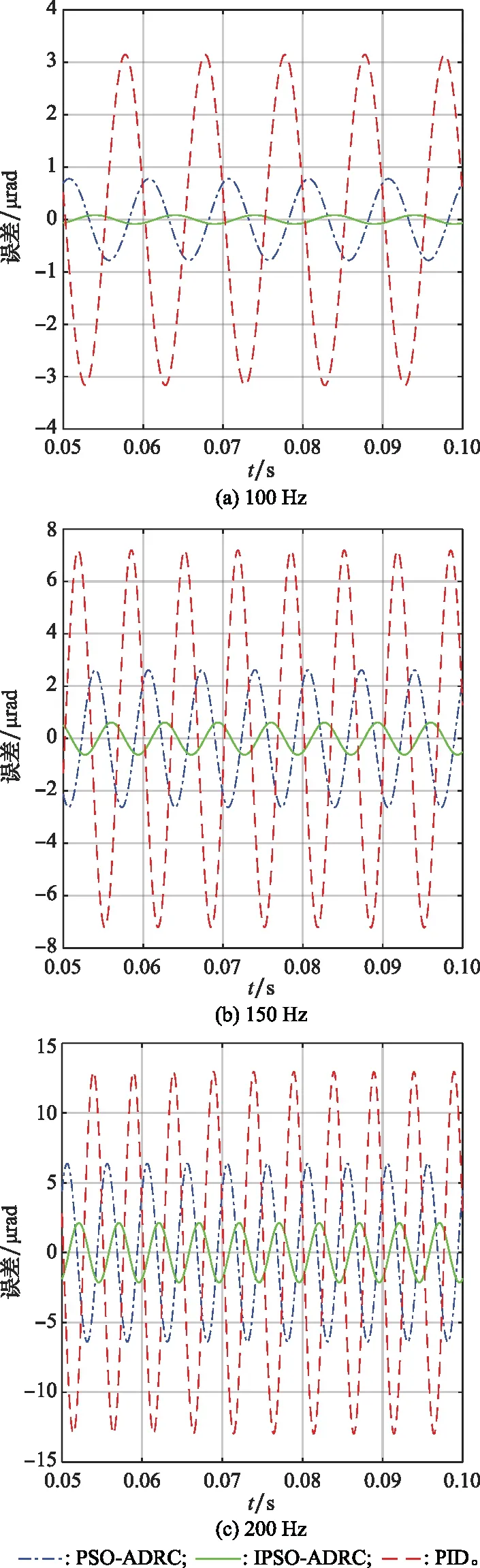
5.3 数值仿真实验

6 结 论
